力扣每日一题114:二叉树展开为链表
题目
中等
提示
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:
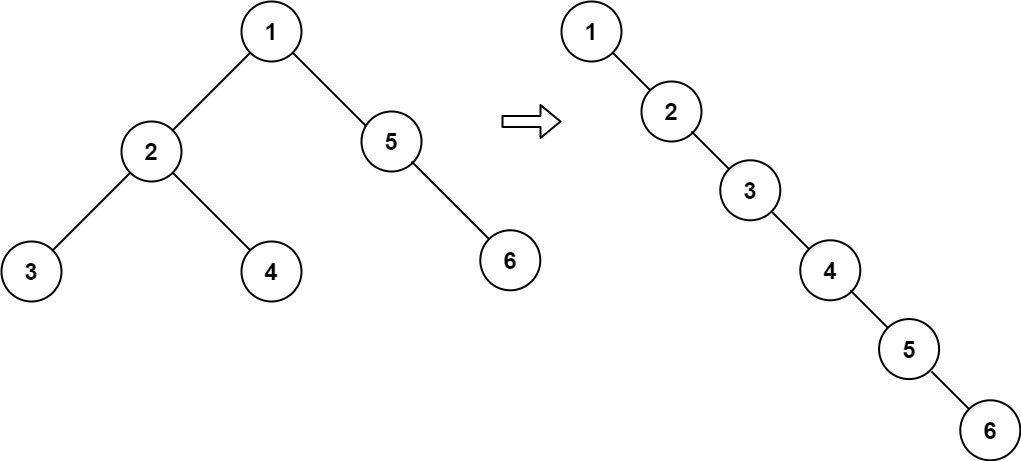
输入:root = [1,2,5,3,4,null,6] 输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [0] 输出:[0]
提示:
- 树中结点数在范围
[0, 2000]内 -100 <= Node.val <= 100
进阶:你可以使用原地算法(O(1) 额外空间)展开这棵树吗?
面试中遇到过这道题?
1/5
是
否
通过次数
465.3K
提交次数
631.8K
通过率
73.6%
结点结构
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/方法一:前序遍历
前序遍历所有的结点,将遍历的结点依次放入一个数组中,然后再转换成单链表。
class Solution {
public:void preorder(TreeNode *root,vector<TreeNode*> &temp){if(!root) return ;temp.push_back(root);preorder(root->left,temp);preorder(root->right,temp);}void flatten(TreeNode* root) {if(!root) return;vector<TreeNode*> temp;preorder(root,temp);temp.push_back(NULL);for(int i=0;i<temp.size()-1;i++){temp[i]->left=NULL;temp[i]->right=temp[i+1];}}
};官解还提供了下面两种方法
方法二:前序遍历和展开同时进行
使用方法一的前序遍历,由于将节点展开之后会破坏二叉树的结构而丢失子节点的信息,因此前序遍历和展开为单链表分成了两步。能不能在不丢失子节点的信息的情况下,将前序遍历和展开为单链表同时进行?
之所以会在破坏二叉树的结构之后丢失子节点的信息,是因为在对左子树进行遍历时,没有存储右子节点的信息,在遍历完左子树之后才获得右子节点的信息。只要对前序遍历进行修改,在遍历左子树之前就获得左右子节点的信息,并存入栈内,子节点的信息就不会丢失,就可以将前序遍历和展开为单链表同时进行。
该做法不适用于递归实现的前序遍历,只适用于迭代实现的前序遍历。修改后的前序遍历的具体做法是,每次从栈内弹出一个节点作为当前访问的节点,获得该节点的子节点,如果子节点不为空,则依次将右子节点和左子节点压入栈内(注意入栈顺序)。
展开为单链表的做法是,维护上一个访问的节点 prev,每次访问一个节点时,令当前访问的节点为 curr,将 prev 的左子节点设为 null 以及将 prev 的右子节点设为 curr,然后将 curr 赋值给 prev,进入下一个节点的访问,直到遍历结束。需要注意的是,初始时 prev 为 null,只有在 prev 不为 null 时才能对 prev 的左右子节点进行更新。
class Solution {
public:void flatten(TreeNode* root) {if (root == nullptr) {return;}auto stk = stack<TreeNode*>();stk.push(root);TreeNode *prev = nullptr;while (!stk.empty()) {TreeNode *curr = stk.top(); stk.pop();if (prev != nullptr) {prev->left = nullptr;prev->right = curr;}TreeNode *left = curr->left, *right = curr->right;if (right != nullptr) {stk.push(right);}if (left != nullptr) {stk.push(left);}prev = curr;}}
};方法三:寻找前驱结点。(类似于Morris遍历)
前两种方法都借助前序遍历,前序遍历过程中需要使用栈存储节点。有没有空间复杂度是 O(1)O(1)O(1) 的做法呢?
注意到前序遍历访问各节点的顺序是根节点、左子树、右子树。如果一个节点的左子节点为空,则该节点不需要进行展开操作。如果一个节点的左子节点不为空,则该节点的左子树中的最后一个节点被访问之后,该节点的右子节点被访问。该节点的左子树中最后一个被访问的节点是左子树中的最右边的节点,也是该节点的前驱节点。因此,问题转化成寻找当前节点的前驱节点。
具体做法是,对于当前节点,如果其左子节点不为空,则在其左子树中找到最右边的节点,作为前驱节点,将当前节点的右子节点赋给前驱节点的右子节点,然后将当前节点的左子节点赋给当前节点的右子节点,并将当前节点的左子节点设为空。对当前节点处理结束后,继续处理链表中的下一个节点,直到所有节点都处理结束。
class Solution {
public:void flatten(TreeNode* root) {TreeNode *curr = root;while (curr != nullptr) {if (curr->left != nullptr) {auto next = curr->left;auto predecessor = next;while (predecessor->right != nullptr) {predecessor = predecessor->right;}predecessor->right = curr->right;curr->left = nullptr;curr->right = next;}curr = curr->right;}}
};相关文章:

力扣每日一题114:二叉树展开为链表
题目 中等 提示 给你二叉树的根结点 root ,请你将它展开为一个单链表: 展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。展开后的单链表应该与二叉树 先序遍历 顺序相同…...

Linux系统下使用LVM扩展逻辑卷的步骤指南
Linux系统下使用LVM扩展逻辑卷的步骤指南 文章目录 Linux系统下使用LVM扩展逻辑卷的步骤指南前言一、逻辑卷管理(LVM)简介二、扩展逻辑卷步骤1. 检查当前的磁盘布局2. 创建新的分区3. 更新内核的分区表4. 初始化新的物理卷5. 将物理卷添加到卷组6. 调整逻…...
探索AI编程新纪元:从零开始的智能编程之旅
提示:Baidu Comate 智能编码助手是基于文心大模型,打造的新一代编码辅助工具 文章目录 前言AI编程概述:未来已来场景需求:从简单到复杂,无所不包体验步骤:我的AI编程初探试用感受:双刃剑下的深思…...

RustGUI学习(iced)之小部件(三):如何使用下拉列表pick_list?
前言 本专栏是学习Rust的GUI库iced的合集,将介绍iced涉及的各个小部件分别介绍,最后会汇总为一个总的程序。 iced是RustGUI中比较强大的一个,目前处于发展中(即版本可能会改变),本专栏基于版本0.12.1. 概述 这是本专栏的第三篇,主要讲述下拉列表pick_list部件的使用,会…...

【OceanBase诊断调优】—— Unit 迁移问题的排查方法
适用版本:V2.1.x、V2.2.x、V3.1.x、V3.2.x 本文主要介绍 OceanBase 数据集在副本迁移过程中遇到的问题的排查方法。 适用版本 V2.1.x、V2.2.x、V3.1.x、V3.2.x 手动调度迁移问题的排查 OceanBase 数据库的 RootService 模块负责 Unit 迁移的调度,如果…...
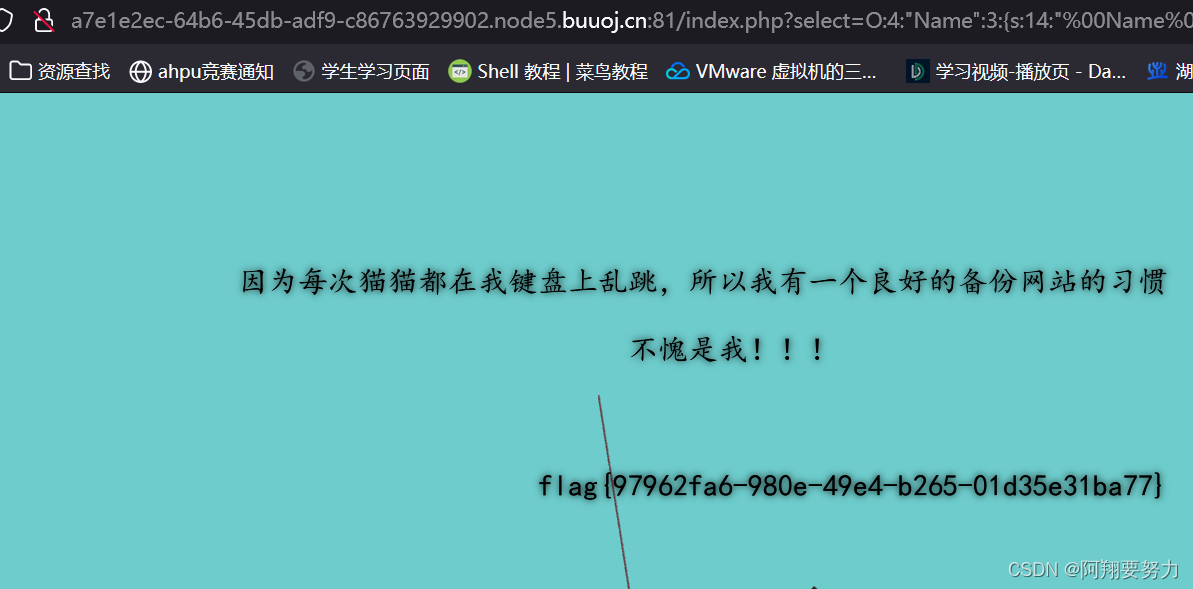
[极客大挑战 2019]PHP
1.通过目录扫描找到它的备份文件,这里的备份文件是它的源码。 2.源码当中涉及到的关键点就是魔术函数以及序列化与反序列化。 我们提交的select参数会被进行反序列化,我们要构造符合输出flag条件的序列化数据。 但是,这里要注意的就是我们提…...
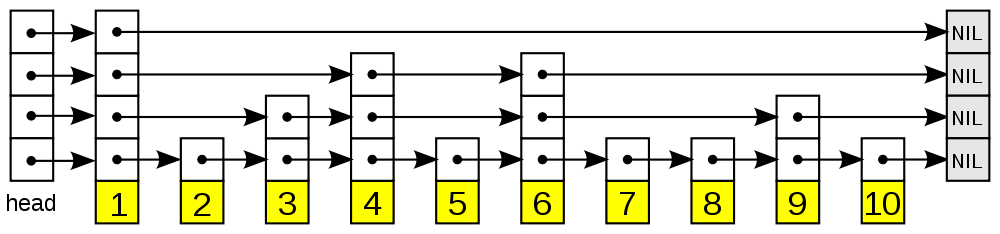
数据结构之跳跃表
跳跃表 跳跃表(skiplist)是一种随机化的数据, 由 William Pugh 在论文《Skip lists: a probabilistic alternative to balanced trees》中提出, 跳跃表以有序的方式在层次化的链表中保存元素, 效率和平衡树媲美 —— …...

搜维尔科技:动作捕捉解决方案:销售、服务、培训和支持
动作捕捉解决方案:销售、服务、培训和支持 搜维尔科技:动作捕捉解决方案:销售、服务、培训和支持l...
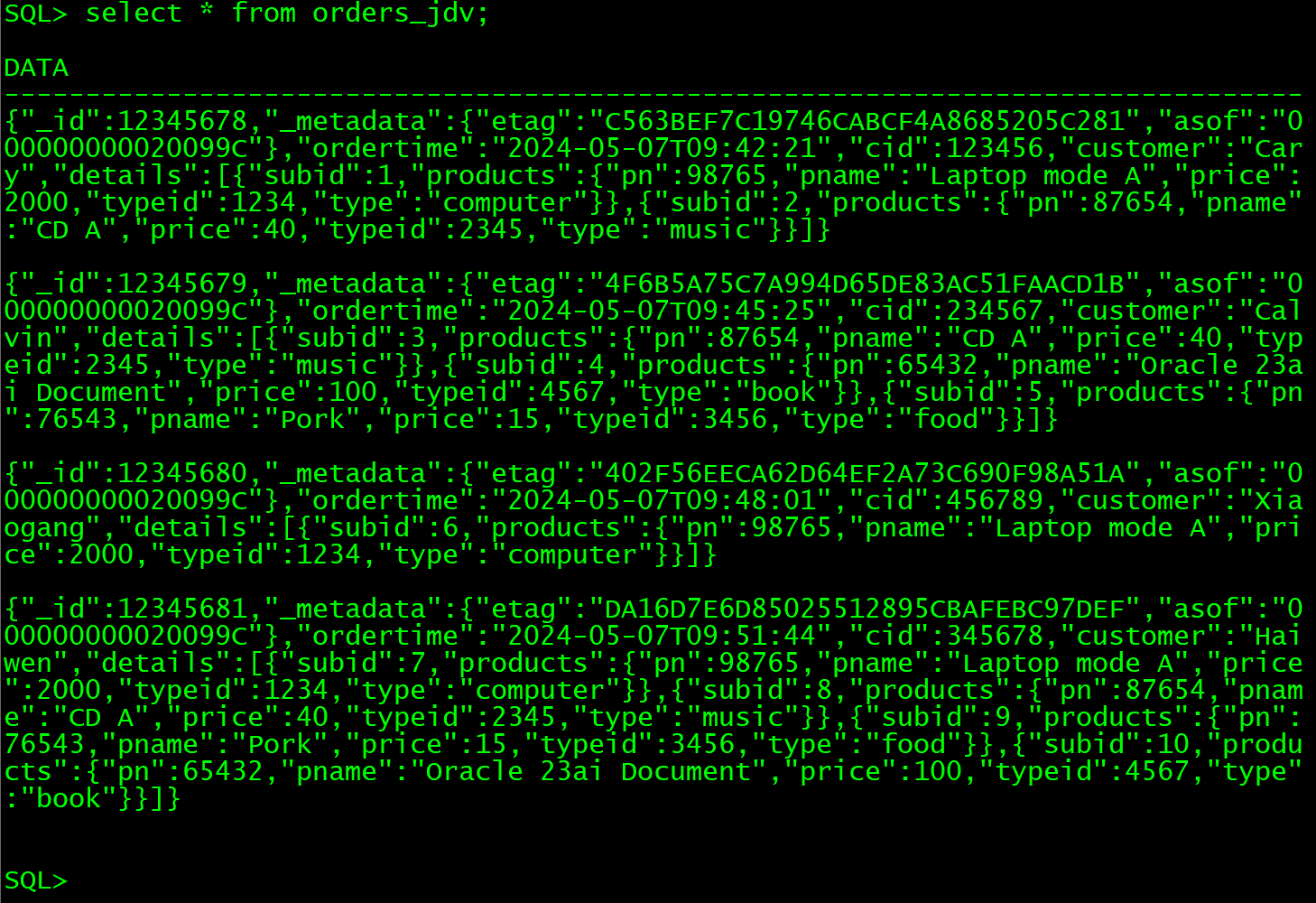
数据库管理-第184期 23ai:干掉MongoDB的不一定是另一个JSON数据库(20240507)
数据库管理184期 2024-05-07 数据库管理-第184期 23ai:干掉MongoDB的不一定是另一个JSON数据库(20240507)1 JSON需求2 关系型表设计3 JSON关系型二元性视图3 查询视图总结 数据库管理-第184期 23ai:干掉MongoDB的不一定是另一个JSON数据库(20…...
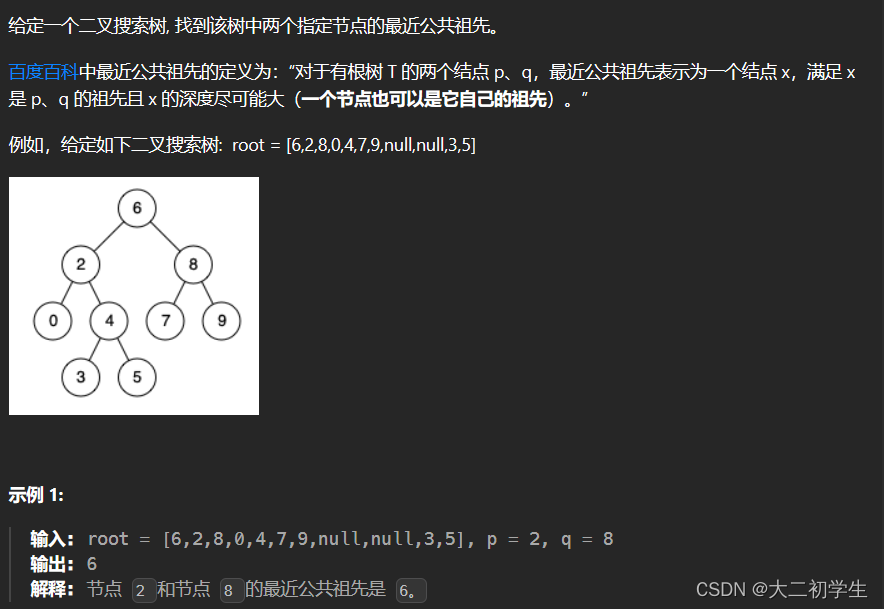
刷代码随想录有感(58):二叉树的最近公共祖先
题干: 代码: class Solution { public:TreeNode* traversal(TreeNode* root, TreeNode* p, TreeNode* q){if(root NULL)return NULL;if(root p || root q)return root;TreeNode* left traversal(root->left, p, q);TreeNode* right traversal(r…...
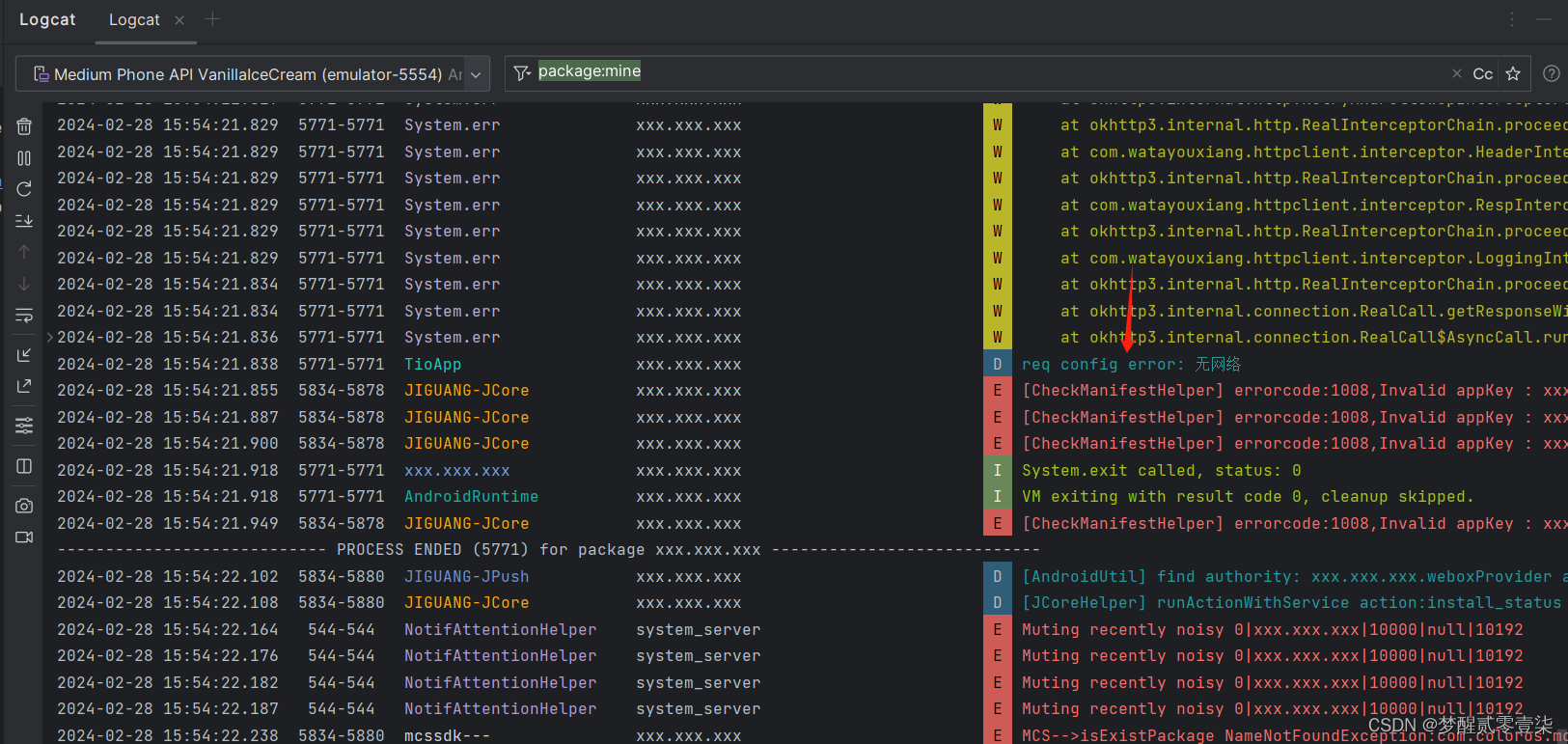
[开发|安卓] Android Studio 开发环境配置
Android Studio下载 Android Studio下载地址 下载SDK依赖 1.点击左上角菜单 2.选择工具 3.打开SDK管理中心 4.下载项目目标Android版本的SDK 配置安卓虚拟机 1.打开右上角的设备管理 2.选择合适的手机规格 3.下载并选择项目目标Android系统 4.点击完成配置 …...
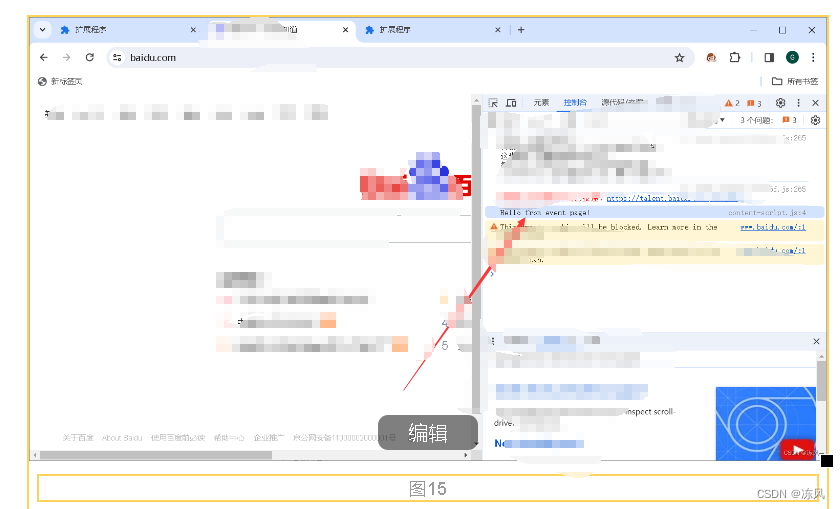
开发 Chrome 浏览器插件入门
目录 前言 一,创建插件 1.创建一个新的目录 2.编写清单文件 二,高级清单文件 1.编写放置右窗口 2.常驻的后台JS或后台页面 3.event-pages 短周期使用 三,Chrome 扩展 API 函数 1.浏览器操作函数 2.内容脚本函数 3.后台脚本函数 4…...
在数字化转型的浪潮中,CBDB百数服务商如何破浪前行?
在信息化时代,传统咨询企业面临着数字化转型的挑战与机遇。如何利用数字化技术提升业务效率、增强客户黏性,成为了行业关注的焦点。云南析比迪彼企业管理有限公司(CBDB)作为云南地区的企业咨询服务提供商,率先与百数展…...

程序员的实用神器
在软件开发的海洋中,程序员的实用神器如同航海中的指南针,帮助他们导航、加速开发、优化代码质量,并最终抵达成功的彼岸。这些工具覆盖了从代码编写、版本控制到测试和部署的各个环节。然而,程序员们通常会有一套自己喜欢的工具集…...
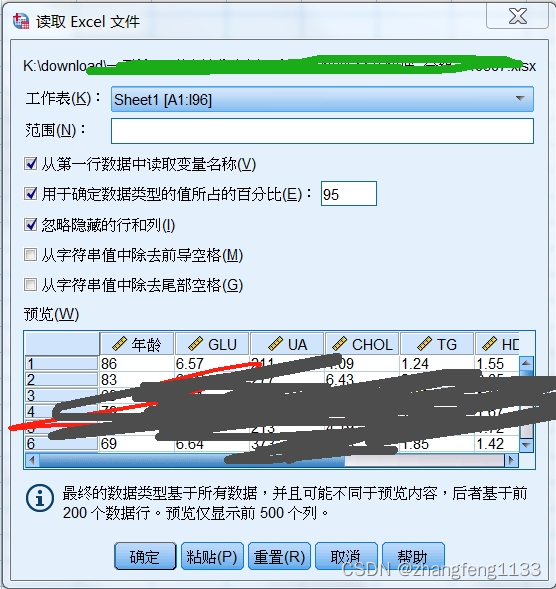
spss 导入数据的时候 用于确定数据类型的值所在的百分比95%是什么意思,数据分析,医学数据分析
在SPSS中,当提及“数据类型的值所在的百分比95%”时,这通常与数据的统计分布或置信区间有关,而不是直接关于数据类型的定义。 导入数据的时候需要定义数据类型,那么根据提供的数据,来定义,有时候ÿ…...

Python进阶之-上下文管理器
✨前言: 🌟什么是上下文管理器? 在Python中,上下文管理器是支持with语句的对象,用于为代码块提供设置及清理代码。上下文管理器广泛应用于资源管理场景,例如文件操作、网络连接、数据库会话等,…...

什么年代了,还在拿考勤说事
最近,看到了某公司的一项考勤规定:自然月内,事假累计超过3次或者累计请假时间超过8小时的,不予审批,强制休假的按旷工处理。 真的想吐槽,什么年代了,还在拿考勤说事,这是什么公司、什…...

泰迪智能科技中职大数据实验室建设(职业院校大数据实验室建设指南)
职校大数据实验室是职校校园文化建设的重要部分,大数据实训室的建设方案应涵盖多个方面,包括硬件设施的配备、软件环境的搭建、课程资源的开发、师资力量的培养以及实践教学体系的完善等。 打造特色,对接生产 社会经济与产业的…...
Qt QThreadPool线程池
1.简介 QThreadPool类管理一个QThread集合。 QThreadPool管理和重新设计单个QThread对象,以帮助降低使用线程的程序中的线程创建成本。每个Qt应用程序都有一个全局QThreadPool对象,可以通过调用globalInstance来访问该对象。 要使用其中一个QThreadPool…...

无人机+三维建模:倾斜摄影技术详解
无人机倾斜摄影测量技术是一项高新技术,近年来在国际摄影测量领域得到了快速发展。这种技术通过从一个垂直和四个倾斜的五个不同视角同步采集影像,从而获取到丰富的建筑物顶面及侧视的高分辨率纹理。这种技术不仅能够真实地反映地物情况,还能…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
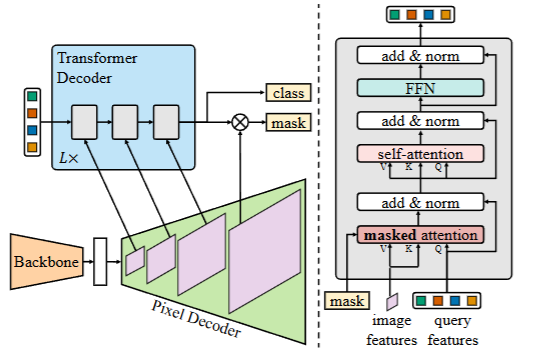
2025-06-08-深度学习网络介绍(语义分割,实例分割,目标检测)
深度学习网络介绍(语义分割,实例分割,目标检测) 前言 在开始这篇文章之前,我们得首先弄明白,什么是图像分割? 我们知道一个图像只不过是许多像素的集合。图像分割分类是对图像中属于特定类别的像素进行分类的过程,即像素级别的…...
