5月7日监控二叉树+斐波那契数
968.监控二叉树
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
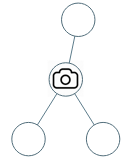
输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
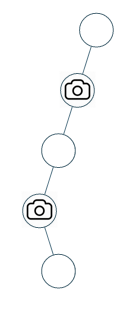
输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
思路
想半天想不出来然后去看了各路大神的题解,对比之下发现官方题解的说法完全是在冒充人类。
首先我们先要确定从二叉树的下面往上看,为什么不自顶向下呢?因为头节点放不放摄像头也就省下一个摄像头,但是叶子节点放不放摄像头省下的是指数级的摄像头。
那么从下往上看我们首先想到的是二叉树的后序遍历法(左-右-中),所以本题我们使用递归法来解。
并且,如果要达成局部最优的话,我们一定是在叶子节点的父节点安装摄像头,让所用摄像头最少,达成全局最优。
所以,大体思路就是从低向上遍历二叉树,先给叶子节点父节点放摄像头,然后隔两个节点放一个摄像头,直到到根节点。
但是怎样隔两个节点放一个摄像头呢?此时我们就需要状态转移的公式来记录每个节点的状态。每个节点可能有三种状态:
0:该节点无覆盖
1:该节点有摄像头
2:该节点有覆盖
空节点一律视为有覆盖的情况,因为若把空节点视为无覆盖,那么空节点的父节点——叶子节点就必须放置一个摄像头,这与本意冲突;若把空节点视为有摄像头,那么叶子节点就为有覆盖,那么隔两个节点才会放一个摄像头,实际上没有监控到叶子节点,所以空节点只能视为有覆盖。
那么,对于每个节点的处理逻辑我们可以分为四类情况:
1、左右节点都有覆盖:该节点一定无覆盖
2、左右节点至少有一个无覆盖:该节点一定放摄像头
3、左右节点至少有一个摄像头:该节点一定有覆盖
4、头节点无覆盖:头节点再加一个摄像头。
代码
class Solution {int res=0;public int minCameraCover(TreeNode root) {return dfs(root)==0?res+1:res;}private int dfs(TreeNode node){if(node==null){return 2;}int left=dfs(node.left);int right=dfs(node.right);if(left==0||right==0){res++;return 1;}if(left==1||right==1){return 2;}return 0;}}灵茶山艾府的思路我没理解,二刷的时候再研究。
509.斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
思路
经典递归解法:
class Solution {public int fib(int n) {if(n==1){return 1;}else if(n==0){return 0;}else {return fib(n-1)+fib(n-2);}}}dp解法:
确定dp数组含义
dp[i]的定义为:第i个数的斐波那契数值为dp[i]
递推公式:dp[i] = dp[i - 1] + dp[i - 2];
初始化:dp[0]=0,dp[1]=1
代码
class Solution {public int fib(int n) {if (n <= 1) return n; int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 1;for (int index = 2; index <= n; index++){dp[index] = dp[index - 1] + dp[index - 2];}return dp[n];}
}空间复杂度可以进一步优化,因为不用维护整个dp数组:
class Solution {public int fib(int n) {if (n < 2) return n;int a = 0, b = 1, c = 0;for (int i = 1; i < n; i++) {c = a + b;a = b;b = c;}return c;}
}相关文章:

5月7日监控二叉树+斐波那契数
968.监控二叉树 给定一个二叉树,我们在树的节点上安装摄像头。 节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。 计算监控树的所有节点所需的最小摄像头数量。 示例 1: 输入:[0,0,null,0,0] 输出:1 解释ÿ…...

C++类的设计编程示例
一、银行账户类 【问题描述】 定义银行账户BankAccount类。 私有数据成员:余额balance(整型)。 公有成员方法: 无参构造方法BankAccount():将账户余额初始化为0; 带参构造方法BankAccount(int m)࿱…...
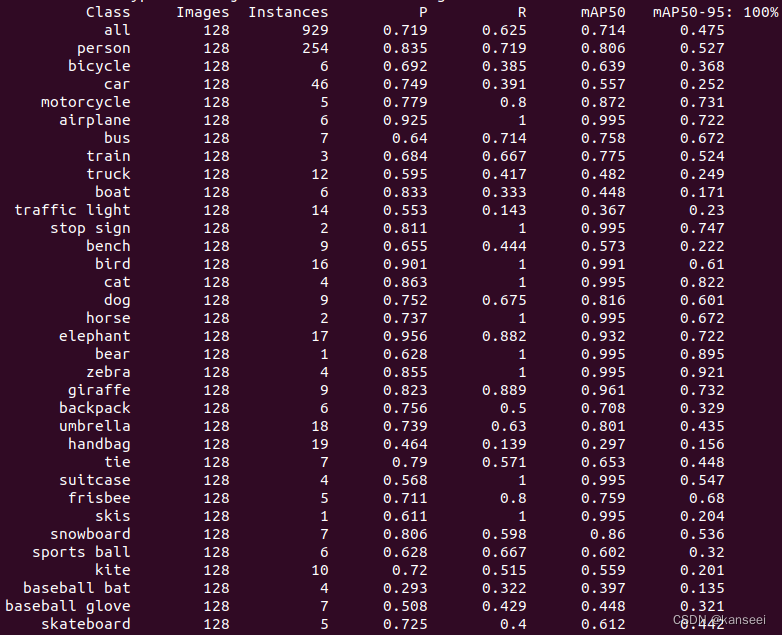
YOLOv5 V7.0 - rknn模型的验证 输出精度(P)、召回率(R)、mAP50、mAP50-95
1.简介 RKNN官方没有提供YOLOv5模型的验证工具,而YOLOv5自带的验证工具只能验证pytorch、ONNX等常见格式的模型性能,无法运行rknn格式。考虑到YOLOv5模型转换为rknn会有一定的精度损失,但是需要具体数值才能进行评估,所以需要一个…...
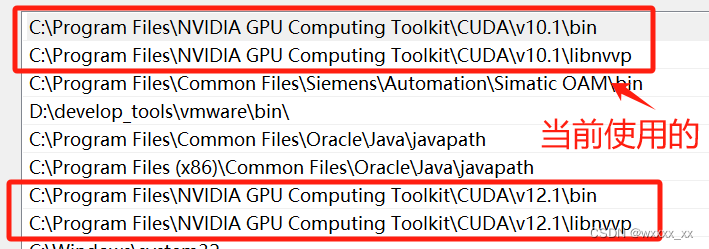
CUDA、CUDNN、Pytorch三者之间的关系
这个东西嘛,我一开始真的是一头雾水,安装起来真是麻烦死了。但是随着要复现的项目越来越多,我也不得不去学会他们是什么,以及他们之间的关系。 首先,一台电脑里面允许有多种版本的cuda存在,然后cuda分为run…...

vue-cli2,vue-cli3,vite 生产环境去掉console.log
console.log一般都是在开发环境下使用的,在生产环境下需要去除 ,如果手动删除未免也太累了,我们可以用插件对于具体环境全局处理。 vue-cli2 项目build 下面webpack.prod.config.js 文件中: plugins: [new webpack.DefinePlugin({process.en…...
Docker-Compose编排LNMP并部署WordPress
前言 随着云计算和容器化技术的快速发展,使用 Docker Compose 编排 LNMP 环境已经成为快速部署 Web 应用程序的一种流行方式。LNMP 环境由 Linux、Nginx、MySQL 和 PHP 组成,为运行 Web 应用提供了稳定的基础。本文将介绍如何通过 Docker Compose 编排 …...

附录C:招聘流程
< 回到目录 附录C:招聘流程 _xxx_公司的招聘 使命 只雇佣顶级人才。 他们是能够胜任工作,并与 _(你的公司名称)_ 的企业文化相匹配的超级明星。 方法 记分卡。招聘经理创建一份文件,详细描述此职位的工作内容…...
1688快速获取整店铺列表 采集接口php Python
在电子商务的浪潮中,1688平台作为中国领先的批发交易平台,为广大商家提供了一个展示和销售商品的广阔舞台;然而,要在众多店铺中脱颖而出,快速获取商品列表并进行有效营销是关键。 竞争对手分析 价格比较:…...

CTF-WEB(MISC)
安全攻防知识——CTF之MISC - 知乎 CTF之MISC杂项从入门到放弃_ctf杂项 你的名字-CSDN博客 CTF MICS笔记总结_archpr 掩码攻击-CSDN博客 一、图片隐写 CTF杂项---文件类型识别、分离、合并、隐写_ctf图片分离-CSDN博客 EXIF(Exchangeable Image File)是…...

Ubuntu如何更换 PyTorch 版本
环境: Ubuntu22.04 WLS2 问题描述: Ubuntu如何更换 PyTorch 版本考虑安装一个为 CUDA 11.5 编译的 PyTorch 版本。如何安装旧版本 解决方案: 决定不升级CUDA版本,而是使用一个与CUDA 11.5兼容的PyTorch版本,您可…...

python flask css样式无效
解释: Flask是一个Python的轻量级Web框架,它没有为CSS提供任何内置的支持。如果你在Flask项目中引入了CSS文件,但是这个CSS没有生效,可能的原因有: 路径不正确:你的CSS文件没有放在正确的目录下࿰…...
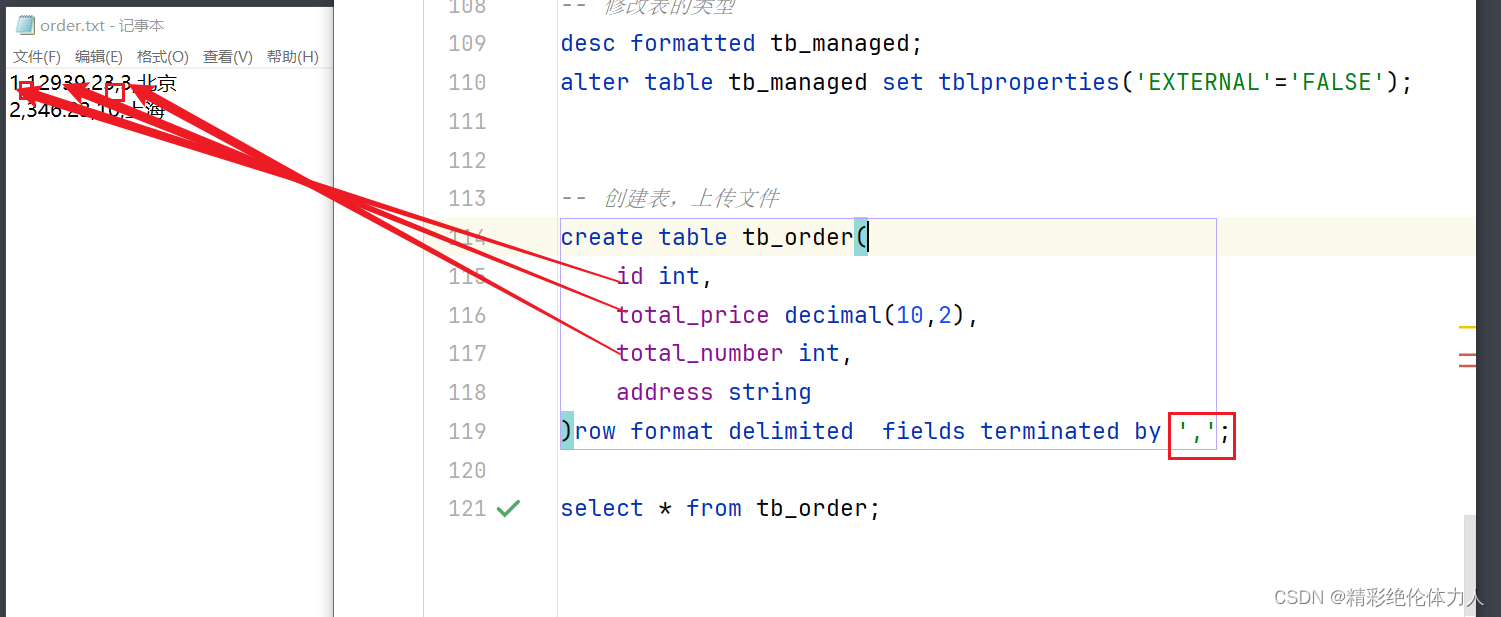
大数据学习笔记14-Hive基础2
一、数据字段类型 数据类型 :LanguageManual Types - Apache Hive - Apache Software Foundation 基本数据类型 数值相关类型 整数 tinyint smallint int bigint 小数 float double decimal 精度最高 日期类型 date 日期 timestamps 日期时间 字符串类型 s…...
)
vue3 下载图片(包括多图片下载)
单图片下载 //使用 download(https://img1.baidu.com/it/u1493209339,2544178769&fm253&app138&sizew931&n0&fJPEG&fmtauto?sec1715101200&t854f3434686cfd2cba9d6a528597d15c)//下载逻辑 const download async (modelUrl) > {const respons…...

LabVIEW如何通过子VI更改主VI控件属性?
在LabVIEW中,可以通过使用Local Variable或Property Node来实现主VI控件属性的更改。这些方法可以在主VI和子VI之间传递数据和控件属性。 Local Variable: 使用Local Variable可以在子VI中直接访问并修改主VI中的控件属性。在子VI中创建Local Variable,并…...

关于MS-DOS时代的回忆
目录 一、MS-DOS是什么? 二、MS-DOS的主要功能有哪些? 三、MS-DOS的怎么运行的? 四、微软开源MS-DOS源代码 五、高手与漂亮女同学 一、MS-DOS是什么? MS-DOS(Microsoft Disk Operating System)是微软公…...
)
数据库索引(Mysql)
简述:数据库索引是加速数据检索,提高查询效率的一种数据结构 语法规则 创建索引 --通用语法规则 --[内容] 可选参数 --UNIQUE: 可选关键字,用于创建唯一索引,确保索引列的值是唯一的 CREATE [UNIQUE] INDEX 索引名 ON 表名(字段名,...) [ASC | DESC];…...

异常-Exception
异常介绍 基本概念 Java语言中,将程序执行中发生的不正常情况称为“异常”。(开发过程中的语法错误和逻辑错误不是异常)执行过程中所发生的异常事件可分为两大类 1,Error(错误):Java虚拟机无法…...
ctfshow——SQL注入
文章目录 SQL注入基本流程普通SQL注入布尔盲注时间盲注报错注入——extractvalue()报错注入——updataxml()Sqlmap的用法 web 171——正常联合查询web 172——查看源代码、联合查询web 173——查看源代码、联合查询web 174——布尔盲注web 176web 177——过滤空格web 178——过…...
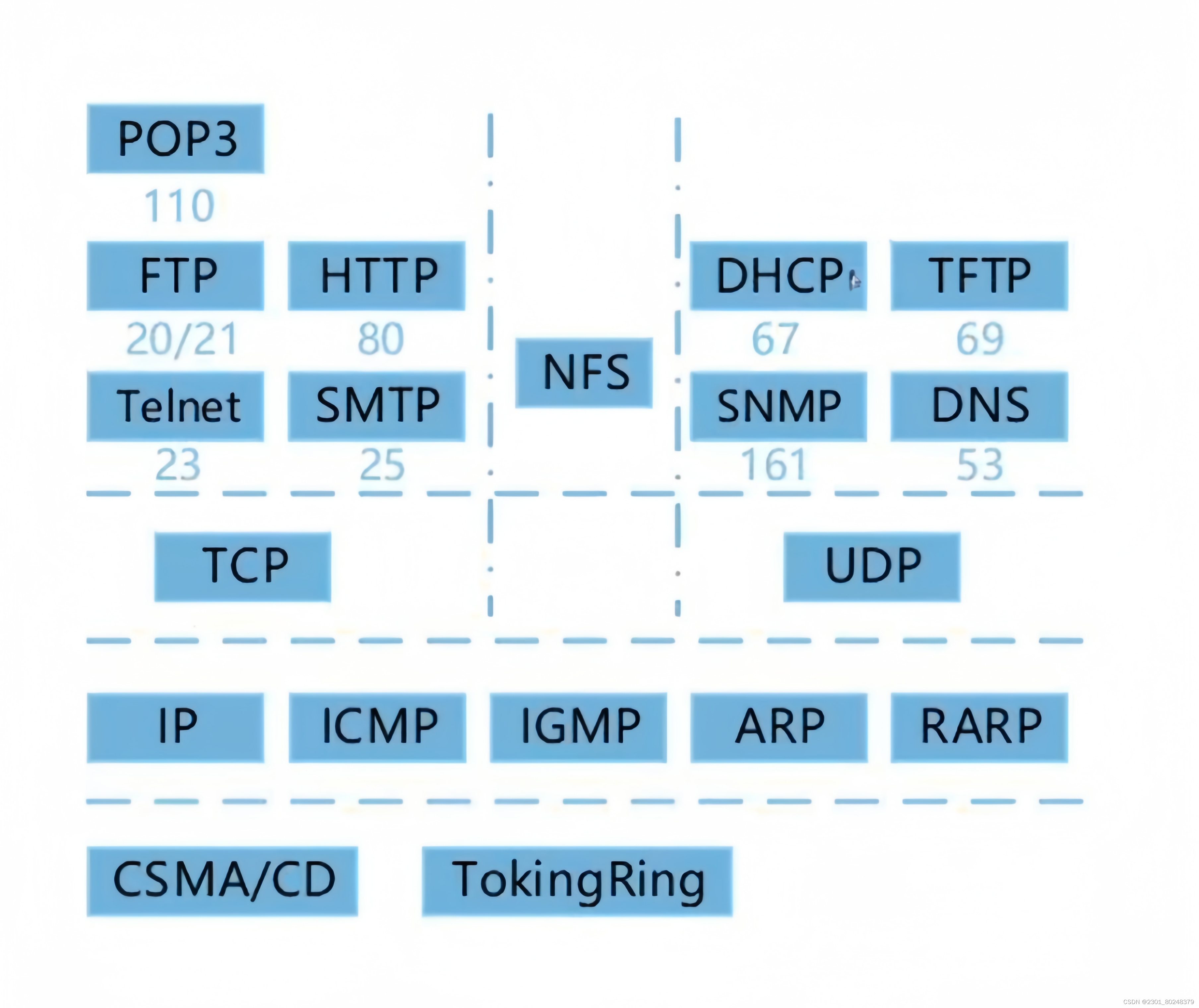
第十三章 计算机网络
这里写目录标题 1.网络设备2.协议簇2.1电子邮件(传输层)2.2地址解析(网际层)2.3DHCP(动态主动配置协议)2.4URL(统一资源定位器)2.5IP地址和子网掩码 1.网络设备 物理层:中继器,集线器(多路中继器) 数据链路层:网桥,交换机(多端口…...

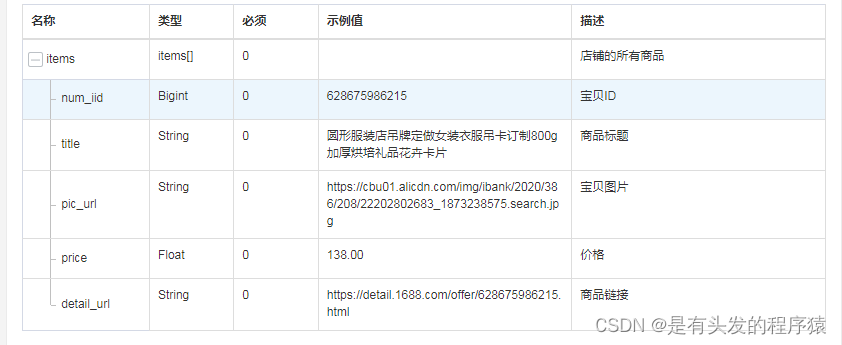
商品详情 API 返回值说明
商品详情API接口在多个领域和场景中都有广泛的应用,以下是一些常见的应用场景: 竞品分析:企业可以利用商品详情API接口获取竞品的所有详细信息,如价格、发货地、上架时间、销售量等。通过分析这些竞品信息,企业可以更…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
