代码随想录训练营
Day45代码随想录
322.零钱兑换
1.题目描述
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
2.解题思路及代码实现
本题注意是最少的组合数,那么dp[j]就代表总额为j所能代表的最少组合数量,如果dp[j-coins[i]]存在那么递推公式为dp[j] = Math.min(dp[j],dp[j-coins[i]]+1);
class Solution {public int coinChange(int[] coins, int amount) {int[] dp = new int[amount+1];for (int i = 0; i <= amount; i++) {dp[i] = Integer.MAX_VALUE;}dp[0] = 0;for (int i = 0; i < coins.length; i++) {for (int j = coins[i]; j <= amount; j++) {if (dp[j-coins[i]]!=Integer.MAX_VALUE)dp[j] = Math.min(dp[j],dp[j-coins[i]]+1);}}return dp[amount]==Integer.MAX_VALUE ? -1:dp[amount];}
}
279.完全平方数
1.题目描述
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
提示:
1 <= n <= 104
2.解题思路及代码实现
其实本题和零钱兑换思路一样,
class Solution {public int numSquares(int n) {int[] dp = new int[n+1];for (int i = 0; i <=n ; i++) {dp[i] = Integer.MAX_VALUE;}dp[0] = 0;for (int i = 1; i <= (int)Math.sqrt(n); i++) {int amount = i*i;for (int j = amount; j <=n ; j++) {if (dp[j-amount]!= Integer.MAX_VALUE)dp[j] = Math.min(dp[j],dp[j-amount]+1);}}return dp[n];}
}
相关文章:

代码随想录训练营
Day45代码随想录 322.零钱兑换 1.题目描述 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -…...
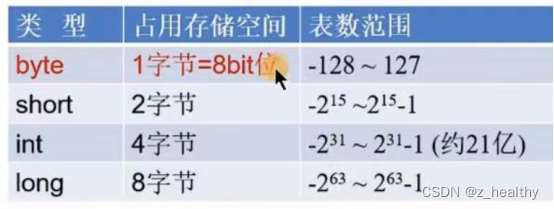
java中的变量、数据类型、人机交互
变量 变量要素 1、类型;每一个变量都需要定义类型(强类型)其它语言有弱类型(js) 2、变量名; 3、存储的值; 声明方式: 数据类型 变量名 变量值; public static vo…...

Python中的生成器是什么
生成器的工作原理 只要Python函数的主体中有yield关键字,该函数就是生成器函数。调用生成器函数,返回一个生成器对象。也就是说,生成器函数是生成器工厂。 下面以一个简单的函数说明生成器的行为: def gen123():yield 1yield 2yield 3print(gen123) # <function gen…...

【Camera2完整流程分析四】从log角度分析CameraService启动流程
下面直接带你通过log打印来一起读CameraService启动的过程。 1)Camera service对象构建,在启动的时候先创建CameraService 这里会打印: CameraService: CameraService started (pid=559)接着启动的时候会执行 –》onFirstRef() 进入这里面看,先输出打印: CameraService:…...

基于SSM SpringBoot vue教务排课系统
基于SSM SpringBoot vue教务排课系统 系统功能 登录 个人中心 学生信息管理 教师信息管理 课室信息管理 班级信息管理 系别信息管理 专业信息管理 课程信息管理 选课信息管理 课表信息管理 开发环境和技术 开发语言:Java 使用框架: SSM(Spring SpringMVC Myba…...
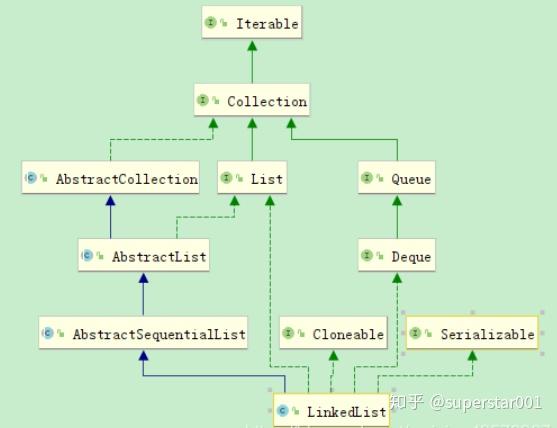
深入理解 LinkedList 及底层源码分析
LinkedList 是基于链表结构的一种 List,在分析 LinkedList 源码前我们先对对链表结构做一个简单的了解。 一、链表的概念 链表是由一系列非连续的节点组成的存储结构,简单分下类的话,链表又分为_单向链表和双向链表,而单向 / 双…...

美易官方:英伟达业绩将难以撑起股价?
美股市场似乎总是对各大公司的业绩表现抱有极大的期待,就像一个永远填不饱的“巨胃”。在这样的市场环境下,即使是业绩骄人的公司也可能难以支撑其股价。英伟达,这家在图形处理单元(GPU)领域享有盛誉的公司,…...

超实用干货!FP独立站引流攻略
在当前的市场环境下,对于希望继续从事FP和黑五类产品销售的商家来说,搭建独立站绝对是一个明智的选择。没有了第三方平台的限制,拥有自己的独立站意味着你可以完全掌控自己的商业策略和操作。 但脱离了平台,独立站推广会更加困难。…...

php之框架底层中间件模式开发实现、array_reduce的应用
众所周知php框架的中间件核心是通过array_reduce实现的 php之框架中间件模式开发实现、array_reduce的应用 1.先写个测试用例看一下函数的特性2.根据执行特性实现中间件 1.先写个测试用例看一下函数的特性 <?phpfunction kernal($a,$b){return $a . " and " .…...

fabric搭建生产网络
fabric搭建生产网络 一、生成组织结构与身份证书 解包 hyperledger-fabric-linux-amd64-2.5.0.tar.gz 1.1、crypto-config.yaml配置文件 ./bin/cryptogen showtemplate > crypto-config.yaml 将crypto-config.yaml内容修改为: # -------------------------…...

聊聊 ASP.NET Core 中间件(二):中间件和筛选器的区别
前言 有些小伙伴看到上一篇文章后,可能会发现中间件和我们之前讲的筛选器非常类似,比如它们都是通过 next 串起来的一系列的组件,并且都可以在请求处理前后执行代码,都可以通过不执行 next 来进行请求的终止。那么筛选器和中间件…...

Nginx配置Https缺少SSL模块
1、Linux下Nginx配置https nginx下载和安装此处就忽略,可自行百度 1.1、配置https 打开nginx配置文件 vim /opt/app/nginx/conf/nginx.conf相关https配置 server {listen 443 ssl; #开放端口server_name echarts.net;#域名#redirect to https#ssl on; #旧版#ssl证…...
超详细——集成学习——Adaboost实现多分类——附代码
资料参考 1.【集成学习】boosting与bagging_哔哩哔哩_bilibili 集成学习——boosting与bagging 强学习器:效果好,模型复杂 弱学习器:效果不是很好,模型简单 优点 集成学习通过将多个学习器进行结合,常可获得比单一…...
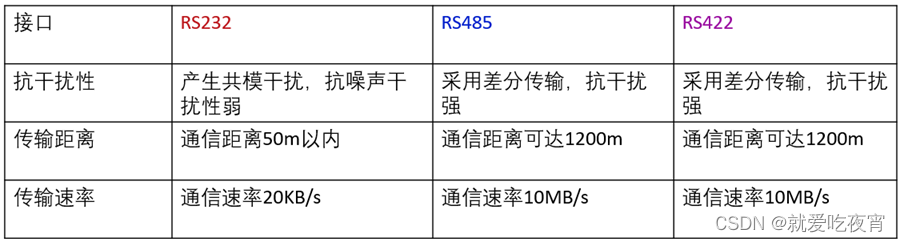
串口通信标准RS232 RS485 RS422的区别
很多工程师经常把RS-232、RS-422、RS-485称为通讯协议,其实这是不对的,它们仅仅是关于串口通讯的一个机械和电气接口标准(顶多是网络协议中的物理层),不是通讯协议,那它们又有哪些区别呢: 第一…...

jdk环境安装
jdk安装 创建软件安装的目录 mkdir -p /bigdata/{soft,server} /bigdata/soft 安装文件的存放目录 /bigdata/server 软件安装的目录 把安装的软件上传到/bigdata/soft 目录 解压到指定目录 -C :指定解压到指定目录 tar -zxvf /bigdata/soft/jdk-8u241-linux-x64.tar.gz -C /b…...
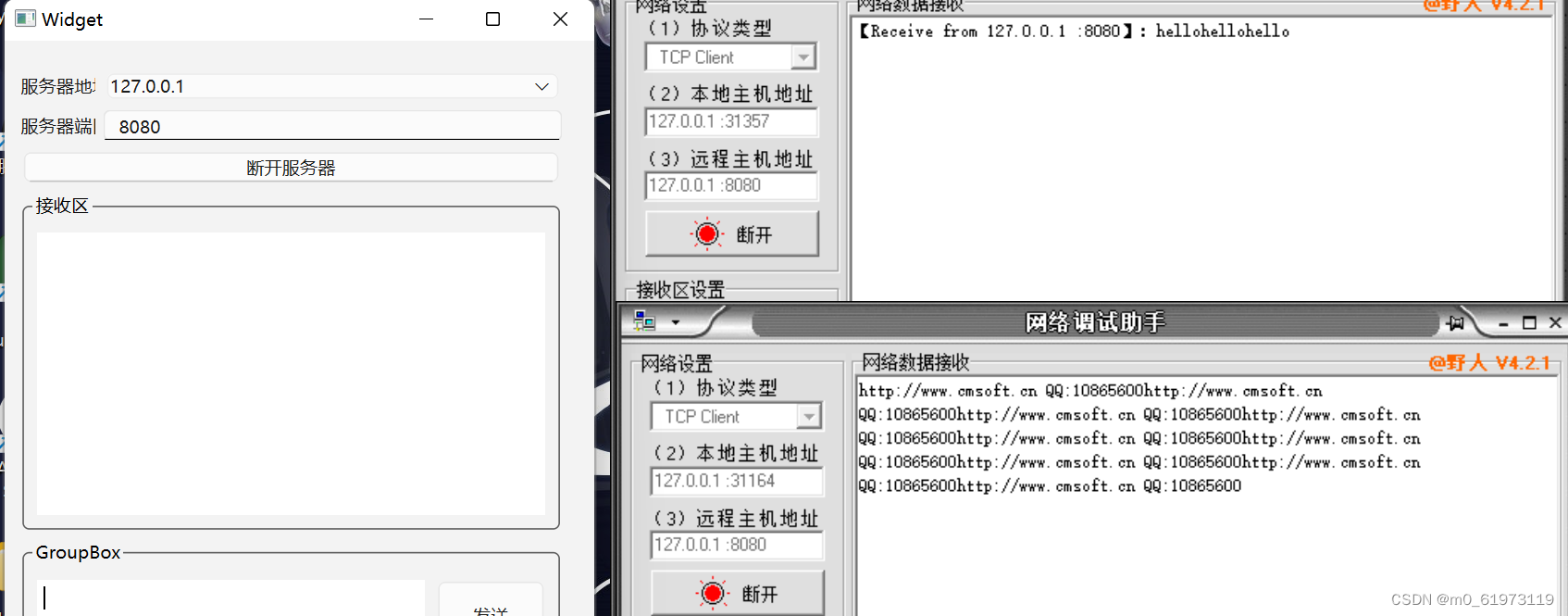
QT+网络调试助手+TCP服务器
一、UI界面设计 二、单线程 代码设计 1、 查找合法的本地地址,用于当作服务器的IP地址 #include <QThread> #include <QTcpSocket> #include <QNetworkInterface> #include <QMessageBox>QList<QHostAddress> ipAddressesList QNe…...
场景)
【unity】(1)场景
Unity的场景(Scene)是构建游戏中各种环境和级别的基础。一个场景可以包含游戏中的所有对象,如角色、道具、地形等。 创建和管理场景 创建新场景: 在Unity编辑器中,选择File > New Scene,或者使用快捷键…...

【Linux】进程间通信IPC机制
目录 一、无名管道 二、有名管道 三、共享内存 四、信号量 五、消息队列 六、套接字 一、无名管道 1.只能用于具有亲缘关系的进程之间的通信(也就是父子进程或者兄弟进程)。 2.是一个单工的通信模式,具有固定的读端和写端。 3.管道也可以看成是一种特殊的文件…...
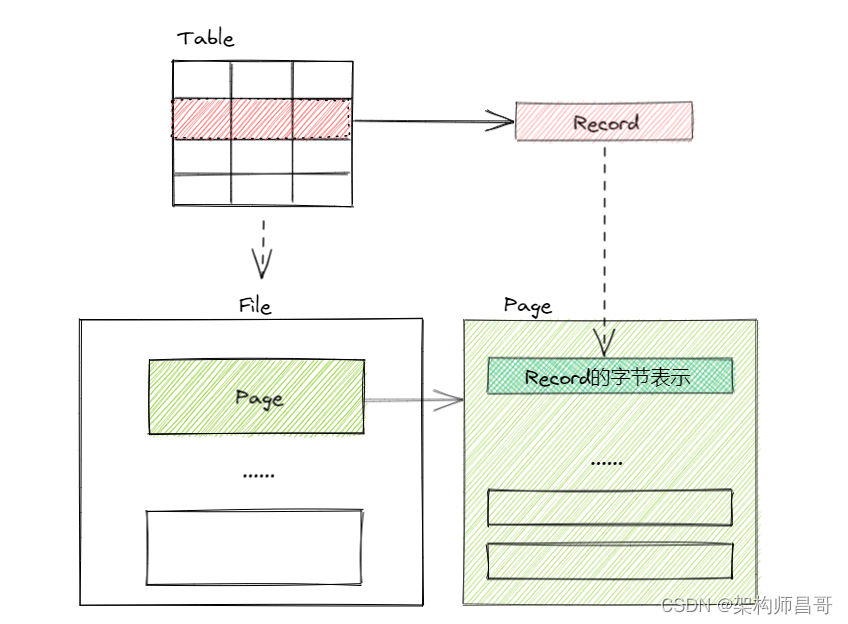
【如此简单!数据库入门系列】之效率基石 -- 磁盘空间管理
文章目录 1 前言2 磁盘空间管理3 磁盘空间管理的实现4 存储对象关系5 总结6 系列文章 1 前言 如何将表中的记录存储在物理磁盘上呢? 概念模式中,记录(Record)表示表中的一行数据,由多个列(字段或者属性&…...
专业渗透测试 Phpsploit-Framework(PSF)框架软件小白入门教程(五)
本系列课程,将重点讲解Phpsploit-Framework框架软件的基础使用! 本文章仅提供学习,切勿将其用于不法手段! 继续接上一篇文章内容,讲述如何进行Phpsploit-Framework软件的基础使用和二次开发。 在下面的图片中&#…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
