动态规划入门和应用示例
文章目录
- 前言
- 斐波那契数列
- 爬楼梯
- 总结
- 优点:
- 缺点:
前言
动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的数学方法。它主要用于解决一类具有重叠子问题和最优子结构性质的问题。通过把原问题分解为相对简单的子问题的方式,动态规划可以求得复杂问题的最优解。
动态规划的基本思想是将一个复杂的问题分解为若干个相对简单的子问题,通过求解这些子问题,并将它们的解存储起来,以便在求解更大的问题时能够重复利用这些解,从而避免大量的重复计算,提高算法的效率。
以下是动态规划入门的几个关键要点:
- 核心思想:
- 动态规划的核心思想是利用过去的数据解决现在的问题。通过分解原问题为相互重叠的子问题,并解决这些子问题来得到原问题的解。
- 动态规划的关键在于“状态”和“状态转移方程”。状态表示问题的某个阶段,而状态转移方程描述了从一个状态转移到另一个状态的规则。
- 基本步骤:
- 定义状态:明确问题中的状态,即子问题的表示方式。
- 状态转移方程:建立状态之间的关系,即如何从当前状态转移到下一个状态。
- 初始化:为状态的初始值设定合理的默认值。
- 计算顺序:按照某种顺序(通常是自底向上或自左向右)计算所有状态的值。
- 返回值:返回最终状态的值作为问题的解。
- 应用实例:
- 斐波那契数列:经典的动态规划问题,可以通过存储已计算的斐波那契数来避免重复计算。
- 背包问题:给定一组物品和背包容量,如何选择物品使得背包内物品的总价值最大。
- 最短路径问题:在图论中,求从一个顶点到另一个顶点的最短路径。
- 股票买卖问题:计算在给定的股票价格序列中,通过买入和卖出股票能够获得的最大利润。
- 实践建议:
- 从简单的问题开始,逐步增加难度,逐步熟悉和掌握动态规划的思想和方法。
- 多做练习,尤其是经典问题的练习,有助于深入理解动态规划的应用和技巧。
- 结合实际问题,思考如何将其转化为动态规划问题,并设计合适的状态和状态转移方程。
总之,动态规划是一种强大而灵活的数学工具,适用于求解各种优化问题。通过不断学习和实践,你可以逐渐掌握这一技术并应用于实际问题中。
斐波那契数列
斐波那契数列是一个常见的动态规划问题,其定义为:每个数是前两个数之和,序列的开始两个数是0和1。例如,斐波那契数列的前几个数是:0, 1, 1, 2, 3, 5, 8, 13, 21, …
在C++中,我们可以使用动态规划来高效地计算斐波那契数列中的数。下面是一个简单的C++代码示例,它使用动态规划来计算第n个斐波那契数:
#include <bits/stdc++.h>int fibonacci(int n) {if (n <= 1) {return n;}std::vector<int> dp(n + 1);dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; ++i) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];
}int main() {int n;std::cout << "Enter the position in the Fibonacci sequence: ";std::cin >> n;std::cout << "Fibonacci number at position " << n << " is: " << fibonacci(n) << std::endl;return 0;
}
在这个代码中,我们创建了一个dp数组来存储斐波那契数列的每一项。数组的索引表示斐波那契数列中的位置,数组的值表示对应位置的斐波那契数。我们从位置2开始迭代,并使用前两项的值来计算当前项的值。最后,我们返回dp[n],即第n个斐波那契数。
注意,这个实现方法对于较大的n值可能不是最高效的,因为它使用了一个大小为n+1的数组来存储中间结果。对于更大的n值,我们可以考虑使用迭代方法而不是动态规划,因为迭代方法只需要存储前两项的值,而不是整个数组。下面是一个迭代方法的示例:
int fibonacci(int n) {if (n <= 1) {return n;}int a = 0, b = 1, temp;for (int i = 2; i <= n; ++i) {temp = a + b;a = b;b = temp;}return b;
}
在这个迭代版本中,我们只使用了三个变量a、b和temp来依次计算斐波那契数列中的每一项,而不是使用整个数组。这种方法在内存使用上更加高效,特别是对于非常大的n值。
爬楼梯
C++ 动态规划入门的一个经典例子就是“爬楼梯”问题。这个问题描述如下:
假设你正在爬楼梯,需要 n 阶你才能到达楼顶。每次你都可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
为了解决这个问题,我们可以使用动态规划。我们可以定义一个数组 dp,其中 dp[i] 表示到达第 i 阶楼梯的方法数。根据题目,我们知道:
- dp[0 = 1(只有1种方法到达第1阶楼梯,即爬1个台阶)
- dp[1] = 2(有2种方法到达第2阶楼梯,即爬1个台阶两次或爬2个台阶一次)
对于 i >= 2 的情况,到达第 i 阶楼梯的方法数等于到达第 i-1 阶楼梯的方法数(再爬1个台阶)加上到达第 i-2 阶楼梯的方法数(再爬2个台阶)。因此,我们可以得到状态转移方程:
dp[i] = dp[i-1] + dp[i-2]
下面是一个使用 C++ 实现的例子:
#include <bits/stdc++.h>int climbStairs(int m) {if (m <= 2) {return n;}//定义m级台阶走法数组int dp[m];//一级台阶1种走法dp[0] = 1; //二级台阶2种走法dp[1] = 2; //第i级台阶走法=第i-1级台阶走法+第i-2级台阶走法for (int i = 2; i < m; ++i) { dp[i] = dp[i - 1] + dp[i - 2]; } return dp[m-1];
}int main() {int n;std::cout << "Enter the number of stairs: ";std::cin >> n;std::cout << "Number of ways to climb " << n << " stairs: " << climbStairs(n) << std::endl;return 0;
}
总结
以下是动态规划的主要优缺点:
优点:
-
高效性:动态规划通过存储子问题的解,避免了重复计算。对于具有大量重叠子问题的情况,动态规划可以显著减少计算量,提高算法效率。
-
全局最优解:动态规划通过自底向上的方式,逐步构建问题的解,保证了最终得到的是全局最优解。在解决优化问题时,动态规划是一种非常有效的工具。
-
结构清晰:动态规划通常将问题分解为一系列相互关联的子问题,并按照一定的顺序逐步求解。这种分解方式使得问题的结构更加清晰,便于理解和实现。
-
适用范围广:动态规划可以应用于多种类型的问题,包括背包问题、最长公共子序列、最短路径问题等。通过合理的状态定义和状态转移方程设计,动态规划可以很好地解决这些问题。
缺点:
-
空间复杂度较高:动态规划通常需要存储大量的子问题解,以便在后续计算中重复利用。这可能导致较高的空间复杂度,特别是在处理大规模问题时,可能需要消耗大量的内存空间。
-
设计难度较大:动态规划的核心在于状态的定义和状态转移方程的设计。对于复杂的问题,如何选择合适的状态和状态转移方程可能是一个挑战。设计不当可能导致算法的正确性无法保证或效率较低。
-
问题依赖性强:动态规划通常针对特定类型的问题进行设计,对于不同类型的问题可能需要采用不同的策略和方法。这使得动态规划具有一定的局限性,不适用于所有类型的问题。
-
可能不是最优解法:虽然动态规划通常能够得到全局最优解,但在某些情况下,可能存在其他更高效的算法或启发式方法来解决相同的问题。因此,在选择算法时需要根据问题的特点进行权衡和比较。
综上所述,动态规划具有高效性和全局最优解的优点,但也可能存在空间复杂度较高和设计难度较大的缺点。在实际应用中,需要根据问题的特点选择合适的算法,并充分利用动态规划的优势来解决实际问题。
相关文章:

动态规划入门和应用示例
文章目录 前言斐波那契数列爬楼梯总结优点:缺点: 前言 动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的数学方法。它主要用于解决一类具有重叠子问题和最优子结构性质的问题。…...
【C语言】精品练习题
目录 题目一: 题目二: 题目三: 题目四: 题目五: 题目六: 题目七: 题目八: 题目九: 题目十: 题目十一: 题目十二: 题目十…...
数据库(MySQL)—— DML语句
数据库(MySQL)—— DML语句 什么是DML语句添加数据给全部字段添加数据批量添加数据 修改数据删除数据 什么是DML语句 在MySQL中,DML(Data Manipulation Language,数据操纵语言)语句主要用于对数据库中的数…...

【最大公约数 并集查找 调和级数】1998. 数组的最大公因数排序
本文涉及知识点 最大公约数 并集查找 调和级数 LeetCode1998. 数组的最大公因数排序 给你一个整数数组 nums ,你可以在 nums 上执行下述操作 任意次 : 如果 gcd(nums[i], nums[j]) > 1 ,交换 nums[i] 和 nums[j] 的位置。其中 gcd(nums…...

iOS实现一个高性能的跑马灯
效果图 该跑马灯完全通过CATextLayer 实现,轻量级,并且通过 系统的位移动画实现滚动效果,避免了使用displaylink造成的性能瓶颈,使用系统动画,系统自动做了很多性能优化,实现更好的性能,并使用…...

MySQL的视图、存储过程、触发器
视图 介绍 视图是一种虚拟存在的表。视图中的数据并不在数据库中实际存在,行和列数据来自定义视图的查询中使用的表,并且是在使用视图时动态生成的。通俗的讲,视图只保存了查询的SQL逻辑,不保存查询结果。所以我们在创建视图的时…...

【图像特征点匹配】
图像特征点匹配 图像特征点匹配是计算机视觉中的一项关键技术,它涉及在两个或多个图像之间寻找并匹配具有独特属性的点,这些点被称为特征点。 立体视觉:通过匹配同一场景的不同视角图像中的特征点,可以重建场景的三维结构。物体识别:通过匹配物体表面的特征点,可以识别和…...

GZIPOutputStream JSON压缩
一、背景 小王瞥了一眼历史记录表,不禁惊呼:“这表怎么这么大?”同事们闻声纷纷围拢过来查看。仔细一瞧,发现这个表的大小竟然超过了3G。主管随即指示小王打开相应的表数据检查,发现其中存储了用户的权限信息…...

毫米波雷达原理(含代码)(含ARS548 4D毫米波雷达数据demo和可视化视频)
毫米波雷达原理 1. 传统毫米波雷达1.1 雷达工作原理1.2 单目标距离估计1.3 单目标速度估计1.4 单目标角度估计1.5 多目标距离估计1.6 多目标速度估计1.7多目标角度估计1.7 总结 3. FMCW雷达数据处理算法4. 毫米波雷达的目标解析(含python代码)5. ARS548 4D毫米波雷达数据demo(含…...

3.1 Gateway之路由请求和转发
1.依赖坐标 <!--网关--><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-gateway</artifactId></dependency><!--服务注册和发现--><dependency><groupId>com.alibab…...

人脸识别开源算法库和开源数据库
目录 1. 人脸识别开源算法库 1.1 OpenCV人脸识别模块 1.2 Dlib人脸识别模块 1.3 SeetaFace6 1.4 DeepFace 1.5 InsightFace 2. 人脸识别开源数据库 2.1 CelebA 2.2 LFW 2.3 MegaFace 2.4 Glint360K 2.5 WebFace260M 人脸识别 (Face Recognition) 是一种基于人的面部…...
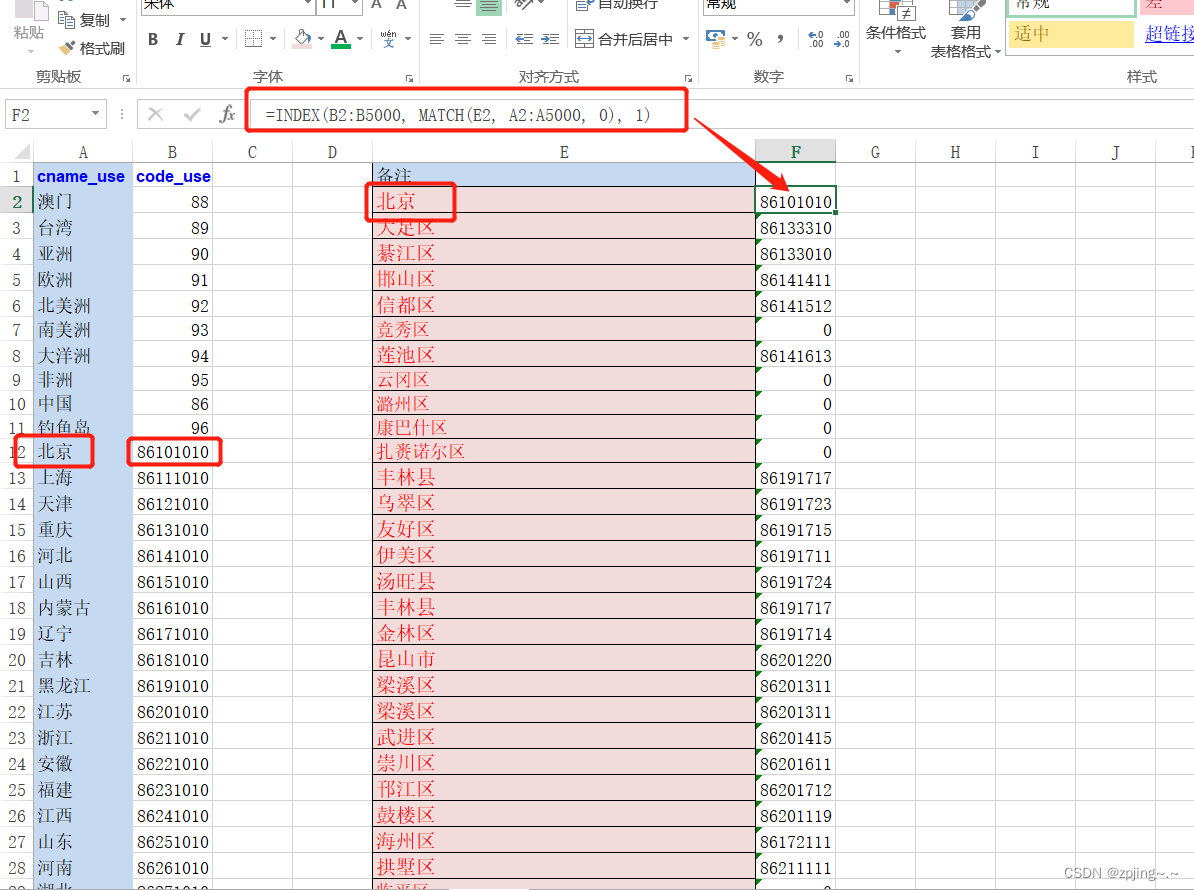
Excel 中用于在一个范围中查找特定的值,并返回同一行中指定列的值 顺序不一样 可以处理吗
一、需求 Excel 中,在一列(某范围内)查找另一列特定的值,并返回同一行中另一指定列的值, 查找列和返回列的顺序不一样 二、 实现 1、下面是一个使用 INDEX 和 MATCH 函数的例子: 假设你有以下数据&…...

MySql-日期分组
一、分别统计各时间各类型数据条数 数据库的 request_time字段 数据类型:timestamp 默认值:CURRENT_TIMESTAMP 例子: 2024-01-26 08:25:48 原数据: 1、将数据按照日期(年月日)形式输出 按照request_…...

有哪些方法可以在运行时动态生成一个Java类?
使用 Java 反射 API🚩: Java 的反射 API 允许在运行时查询和操作类和对象。虽然反射 API 本身不直接提供生成新类的功能,但可以用于动态调用构造函数、方法和访问字段,这在某些情况下可以作为动态生成类的一部分。 字节码操作库&…...

JAVA两个线程交替打印实现
方案1 Semaphore 机制 通过信息号机制来 协调两个线程,一个线程打印后,给另一个线程释放一个信号量 Semaphore semaphorea new Semaphore(1);Semaphore semaphoreb new Semaphore(0);Thread threada new Thread(new Runnable() {Overridepublic void…...

【C语言】学习C语言
C语言简介 C语言是一门十分流行的编程语言,由美国贝尔实验室的 Dennis Ritchie 在 20 世纪 70 年代开发。 C语言具有高效、可移植、灵活、简单等特点,被广泛应用于操作系统、编译器、数据库、图形界面、嵌入式系统、网络通信、游戏等领域。 本文将带你…...

C 深入指针(2)
目录 1 野指针 1.1 成因 1.2 如何规避野指针 2 assert 断言 2.1 用法 2.2 assert 的优点 2.1 assert 的缺点 3 小注解 3.1 Debug 和 Release 1 野指针 【概念】: 野指针就是指针指向的位置是不可知的(随机的、不正确的、没有明确限制的&#…...
FileLink跨网文件交换,推动企业高效协作|半导体行业解决方案
随着信息技术的迅猛发展,全球信息产业已经迎来了前所未有的繁荣与变革。在这场科技革命中,半导体作为信息产业的基础与核心,其重要性日益凸显,半导体的应用场景和市场需求将进一步扩大。 然而,在这一繁荣的背后&#x…...

代码随想录day56 | 动态规划P16 | ● 583. ● 72. ● 编辑距离总结篇
583. 两个字符串的删除操作 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 示例 1: 输入: word1 "sea", word2 "eat" 输出: 2 解释: 第一步将 &quo…...

ASP.NET网络在线考试系统
摘 要 随着计算机技术的发展和互联网时代的到来,人们已经进入了信息时代,也有人称为数字化时代。数在数字化的网络环境下,学生希望得到个性化的满足,根据自己的情况进行学习,同时也希望能够得到科学的评价,…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...
