SQL如何利用Bitmap思想优化array_contains()函数
目录
0 问题描述
1 位图思想
2 案例实战
3 小结
0 问题描述
在工作中,我们往往使用array_contains()函数来进行存在性问题分析,如判断某个数是否在某个数组中,但是当表数据量过多,存在大量array_contains()函数时,就会存在一定性能问题,为了优化该函数的性能,本文主要利用位图的方法来代替array_contains()函数。
1 位图思想
在本文之前读者需要先了解位图的概念及位图的一些性质,本文关于位图的概念不再重复。假如我们有如下需求,如下图所示,我们想判读数字2,5,7是否在数组[1,2,3,5,6]中时,如果用位图我们应该怎么做?通过两个位图相与就可以求出交集,通过下图可以看出bitmap1&bitmap2,可以求出交集2和5在数组中,因此关于此性质,我们可以得到判读存在性问题时,我们只需要构建两个位图与,结果有值不为0则为存在,那么问题来了,如何通过SQL的形式去构建呢?
相比大家对8421码比较熟悉,如1111,如下图所示

上述的式子我们可以进行如下等价
1111=15=1*2^0 + 1 * 2^1 + 1 * 2^2 + 1 * 2^3 <=> 1 << 0 + 1 << 1 + 1 << 2 + 1 << 3
因此我们构建数组 [1,2,3,5,6] 在位图中反应即为:
存在记为1,不存在记为0,即序列 01101110

那我们如何用SQL语言反应上述表达式呢?根据前面的等价转换,我们知道要反应01101110序列
即为:01101110=1*2^1 + 1*2^2 + 1*2^3 + 1*2^5 + 1*2^6 = 1 << 1 + 1 << 2 + 1 << 3 + 1 << 5 + 1 << 6。因此只要我们数据库中支持位移运算,就可以等价上述表达式。那么我们怎么判断数字2是否在上述数组中呢?数字2的位图根据以上推导,我们可以很快得出 1 << 2,而是否存在,只需要两者之间进行与运算即可,即:(1 << 2) &( 1 << 1 + 1 << 2 + 1 << 3 + 1 << 5 + 1 << 6),计算过程如下:
01101110
& 00000010
————————————————
00000010 =2
总结上述规律,我们得出如下判断公式:
假设判断某个num是否在数组[a,b,c,d]中时,可用如下公式:
if{(1 << num) & (1 << a + 1 << b + 1 << c + 1 << d) = num
then true
else false};
上述操作对应不同数据库操作符不一样,如何hive中使用shiftleft函数,doris中采用bit_shift_ left()函数,greenplum中直接为 <<操作符。
2 案例实战
如下2张表tbl1,tbl2,假设表数据量很大,判断tbl2中的col1字段是否在表tbl1中对应的id num字段中。
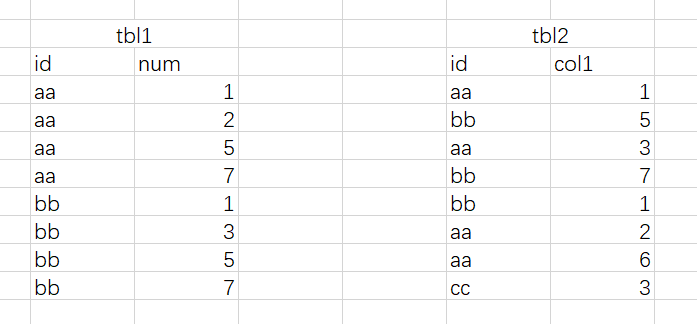
具体SQL如下:
select t1.id, col1,case when (1 << col1) & num ) = col1 then true else false end true_or_false_flgfrom tbl1 t1
left join
(select id ,sum(1 << num) numfrom tbl2group by id ) t2
on t1.id = t2.id读者在遇到相关问题时,可以根据自己具体的场景进行等价变换,这里只是抛砖引玉说明具体使用方法、
3 小结
本文主要阐述了如何利用位图思想优化array_contains()函数的方法,在具体业务中得到了较好的性能提升,当表数据量比较大,且利用array_contains()函数比较多时候,性能提升明显,利用计算机底层位移运算减少了开销。
相关文章:

SQL如何利用Bitmap思想优化array_contains()函数
目录 0 问题描述 1 位图思想 2 案例实战 3 小结 0 问题描述 在工作中,我们往往使用array_contains()函数来进行存在性问题分析,如判断某个数是否在某个数组中,但是当表数据量过多,存在大量array_contains()函数时,…...
面试官:打开了一个新窗口,怎么知道这个窗口已经被打开过?
前言 我们现在来想这么一个场景,在掘金的文章管理页打开了一篇文章草稿,然后点击编辑,这个时候打开新标签页 A ,再点击一次编辑,打开了标签页 B 。 此时如果你在 A 编辑, B 是感知不到 A 的内容变动的&am…...
机器学习项目实践-基础知识部分
环境建立 我们做项目第一步就是单独创建一个python环境,Python新的隔离环境 创建:python -m venv ml 使用:.\Scripts\activate python -m venv ml 是在创建一个名为 ml 的虚拟环境,这样系统会自动创建一个文件夹ml,…...

CNN卷积神经网络,TensorFlow面试题
目录 CNN卷积神经网络 什么是TensorFlow? 张量是什么 TensorFlow有什么优势?...

Android 官网Ota介绍
构建 OTA 软件包 | Android 开源项目 | Android Open Source Project...
Redis(持久化)
文章目录 1.RDB1.介绍2.RDB执行流程3.持久化配置1.Redis持久化的文件是dbfilename指定的文件2.配置基本介绍1.进入redis配置文件2.搜索dbfilename,此时的dump.rdb就是redis持久化的文件3.搜索dir,每次持久化文件,都会在启动redis的当前目录下…...
基于Flask的岗位就业可视化系统(一)
🌟欢迎来到 我的博客 —— 探索技术的无限可能! 🌟博客的简介(文章目录) 前言 本项目综合了基本数据分析的流程,包括数据采集(爬虫)、数据清洗、数据存储、数据前后端可视化等 推荐…...
)
嵌入式学习68-C++(运算符重载和虚函数)
知识零碎: cin >> n 相当于scanf C系统提供的6种基本函数 …...

UVA1048/LA3561 Low Cost Air Travel
UVA1048/LA3561 Low Cost Air Travel 题目链接题意输入格式输出格式 分析AC 代码 题目链接 本题是2006年ICPC世界总决赛的A题 题意 很多航空公司都会出售一种联票,要求从头坐,上飞机时上缴机票,可以在中途任何一站下飞机。比如,假…...
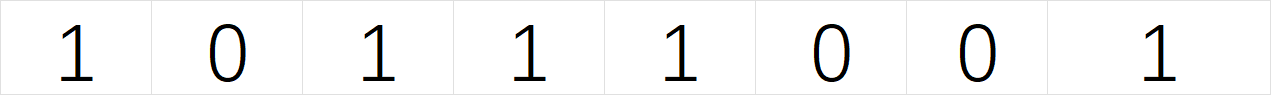
学习和分析各种数据结构所要掌握的一个重要知识——CPU的缓存利用率(命中率)
什么是CPU缓存利用率(命中率),我们首先要把内存搞清楚。 硬盘是什么,内存是什么,高速缓存是什么,寄存器又是什么? 我们要储存数据就要运用到上面的东西。首先里面的硬盘是可以无电存储的&#…...

IOS自动化—将WDA打包ipa批量安装驱动
前言 CSDN: ios自动化-Xcode、WebDriverAgent环境部署 ios获取原生系统应用的包 如果Mac电脑没有配置好Xcode相关环境,可以参考以上文章。 必要条件 Mac电脑,OS版本在12.4及以上(低于这个版本无法安装Xcode14,装不了Xcode14就…...
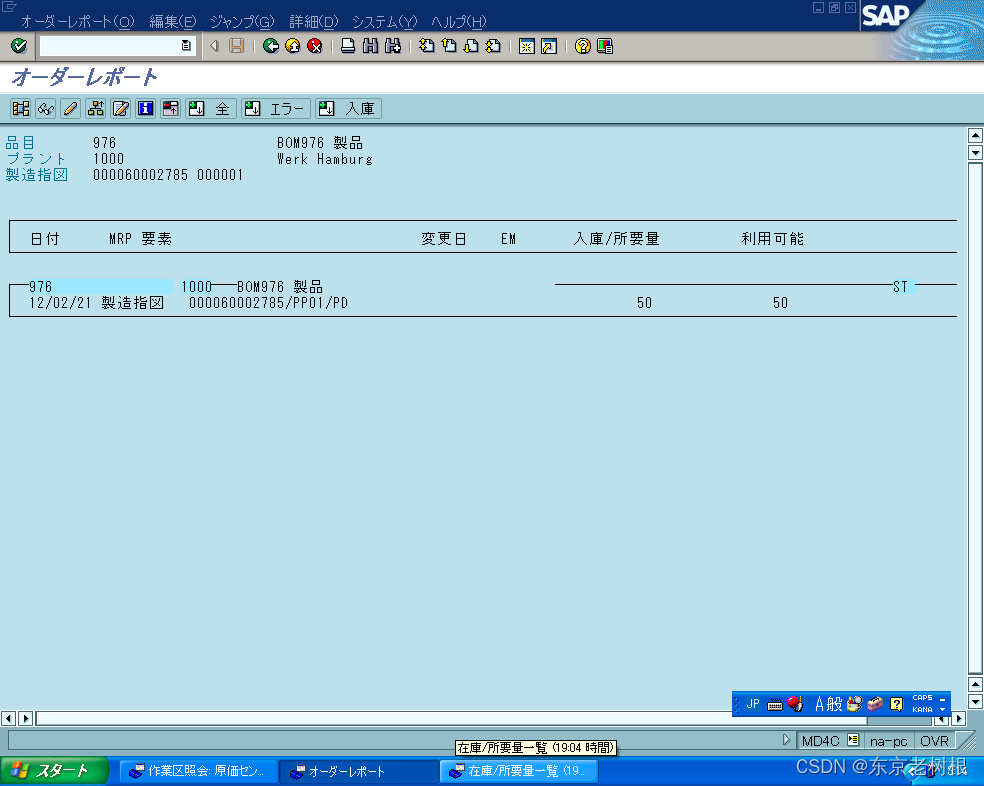
SAP PP学习笔记12 - 评估MRP的运行结果
上一章讲了MRP的概念,参数,配置等内容。 SAP PP学习笔记11 - PP中的MRP相关概念,参数,配置-CSDN博客 本章来讲 MRP跑完之后呢,要怎么评估这个MRP的运行结果。 1,Stock/Requirements List and MRP List 在…...
AndroidStudio的Iguana版的使用
1.AndroidStudio介绍 Android Studio 是用于开发 Android 应用的官方集成开发环境 (IDE)。Android Studio 基于 IntelliJ IDEA 强大的代码编辑器和开发者工具,还提供更多可提高 Android 应用构建效率的功能,例如: 基于 Gradle 的灵活构建系统…...

通过方法引用获取属性名的底层逻辑是什么?
很多小伙伴可能都用过 MyBatis-Plus,这里边我们构造 where 条件的时候,可以直接通过方法引用的方式去指定属性名: LambdaQueryWrapper<Book> qw new LambdaQueryWrapper<>(); qw.eq(Book::getId, 2); List<Book> list bo…...

自学错误合集--项目打包报错,运行报错持续更新中
java后端自学错误总结 一.项目打包报错2.项目打包之后运行报错 二.项目运行报错 一.项目打包报错 javac: �Ҳ����ļ�: E:\xx\xx\xx\docer-xx\src\main\java\xx\xx\xx\xx\xx\xx.java �ÿ…...
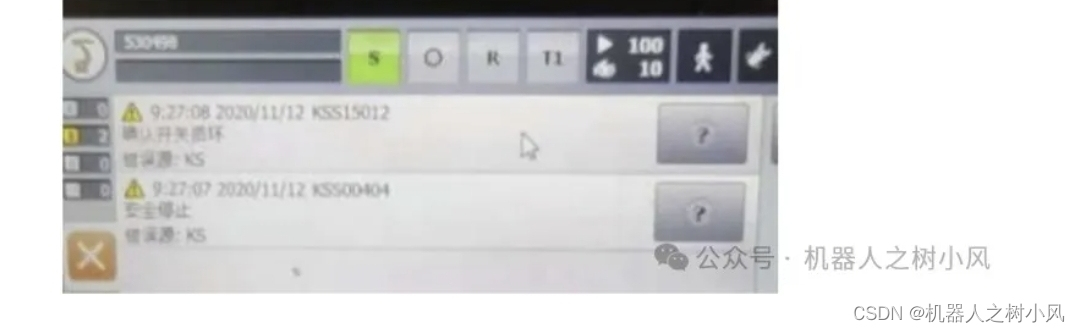
KUKA机器人故障报警信息处理(一)
1、KSS00276 机器人参数不等于机器人类型 ①登录专家模式 ②示教器操作:【菜单】—【显示】—【变量】—【单个】 ③名称输入:$ROBTRAFO[] 新值:TRAFONAME[] ④点击【设定值】。 2、电池报警: ①“充电电池警告-发现老化的蓄电池…...
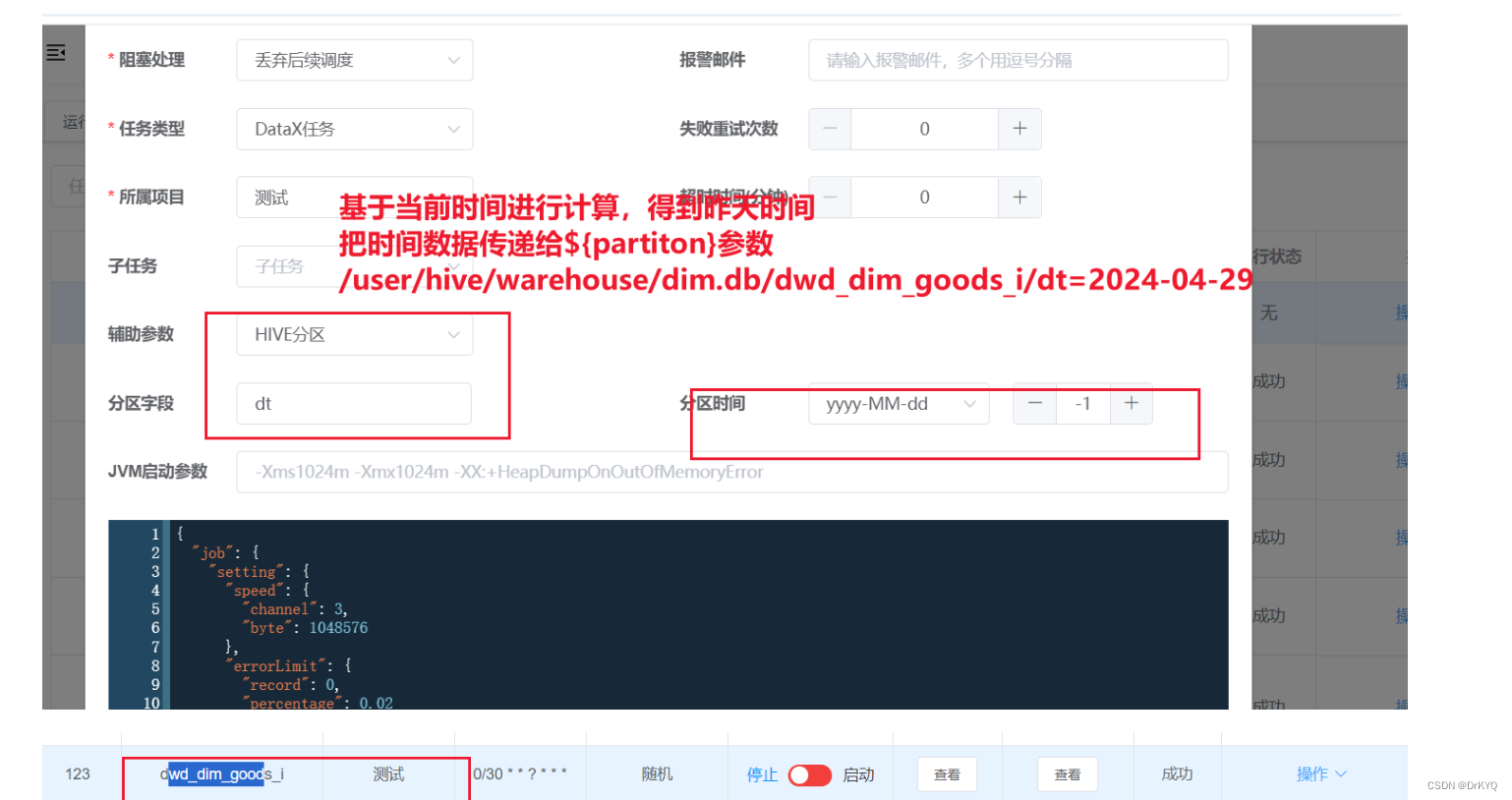
数仓开发:DIM层数据处理
一、了解DIM层 这个就是数仓开发的分层架构 我们现在是在DIM层,从ods表中数据进行加工处理,导入到dwd层,但是记住我们依然是在DIM层,而非是上面的ODS和DWD层。 二、处理维度表数据 ①先确认hive的配置 -- 开启动态分区方案 -- …...
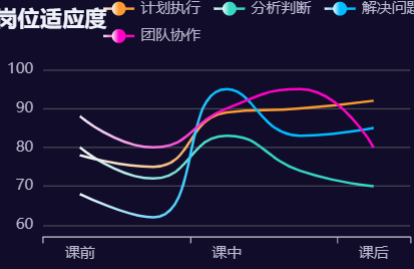
echars设置渐变颜色的方法
在我们日常的开发中,难免会遇到有需求,需要使用echars设置渐变的图表,如果我们需要设置给图表设置渐变颜色的话,我们只需要在 series 配置项中 添加相应的属性配置项即可。 方式一:colorStops type:‘lin…...
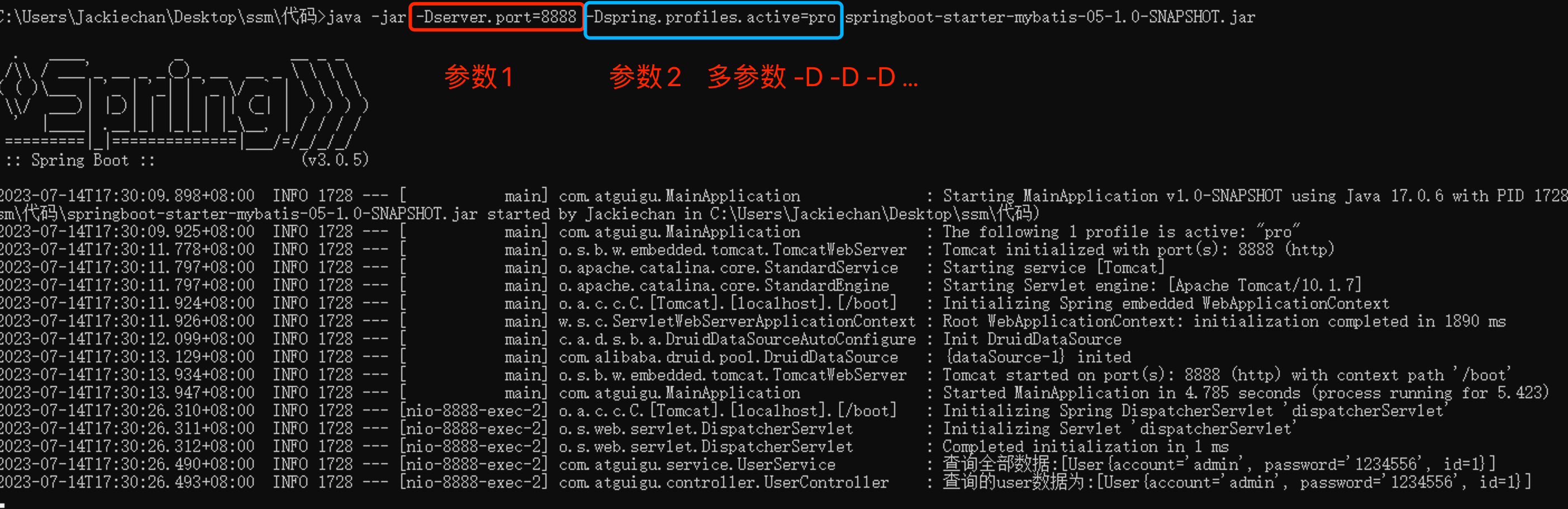
SpringBoot3项目打包和运行
六、SpringBoot3项目打包和运行 6.1 添加打包插件 在Spring Boot项目中添加spring-boot-maven-plugin插件是为了支持将项目打包成可执行的可运行jar包。如果不添加spring-boot-maven-plugin插件配置,使用常规的java -jar命令来运行打包后的Spring Boot项目是无法找…...

Spring Cloud Gateway的部署
不要将 Spring Cloud Gateway 部署到 Tomcat 可以将Spring Cloud Gateway打成jar包,并通过jar包部署,步骤: 1. 修改构建配置 确保你的pom.xml文件中的打包方式为jar。 <packaging>jar</packaging> 2 打包项目 mvn clean pack…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

