【机器学习与实现】线性回归示例——波士顿房价分析
目录
- 一、创建Pandas对象并查看数据的基本情况
- 二、使用皮尔逊相关系数分析特征之间的相关性
- 三、可视化不同特征与因变量'MEDV'(房价中值)间的相关性
- 四、划分训练集和测试集并进行回归分析
一、创建Pandas对象并查看数据的基本情况
boston.csv数据集下载:

链接:https://pan.quark.cn/s/fc4b2415e371
提取码:ZXjU
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inlinehouse = pd.read_csv("boston.csv")
print("shape=", house.shape)
shape= (506, 14)
house[:5]
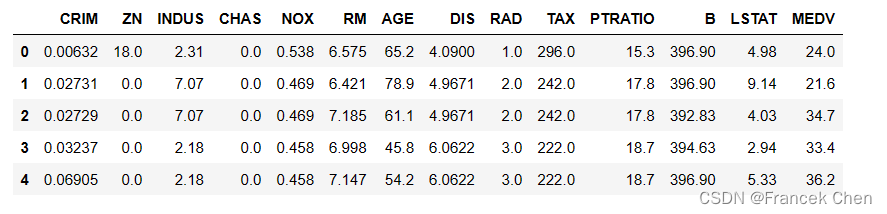
house.describe()
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | MEDV | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 |
| mean | 3.593761 | 11.363636 | 11.136779 | 0.069170 | 0.554695 | 6.284634 | 68.574901 | 3.795043 | 9.549407 | 408.237154 | 18.455534 | 356.674032 | 12.653063 | 22.532806 |
| std | 8.596783 | 23.322453 | 6.860353 | 0.253994 | 0.115878 | 0.702617 | 28.148861 | 2.105710 | 8.707259 | 168.537116 | 2.164946 | 91.294864 | 7.141062 | 9.197104 |
| min | 0.006320 | 0.000000 | 0.460000 | 0.000000 | 0.385000 | 3.561000 | 2.900000 | 1.129600 | 1.000000 | 187.000000 | 12.600000 | 0.320000 | 1.730000 | 5.000000 |
| 25% | 0.082045 | 0.000000 | 5.190000 | 0.000000 | 0.449000 | 5.885500 | 45.025000 | 2.100175 | 4.000000 | 279.000000 | 17.400000 | 375.377500 | 6.950000 | 17.025000 |
| 50% | 0.256510 | 0.000000 | 9.690000 | 0.000000 | 0.538000 | 6.208500 | 77.500000 | 3.207450 | 5.000000 | 330.000000 | 19.050000 | 391.440000 | 11.360000 | 21.200000 |
| 75% | 3.647422 | 12.500000 | 18.100000 | 0.000000 | 0.624000 | 6.623500 | 94.075000 | 5.188425 | 24.000000 | 666.000000 | 20.200000 | 396.225000 | 16.955000 | 25.000000 |
| max | 88.976200 | 100.000000 | 27.740000 | 1.000000 | 0.871000 | 8.780000 | 100.000000 | 12.126500 | 24.000000 | 711.000000 | 22.000000 | 396.900000 | 37.970000 | 50.000000 |
house.info()

二、使用皮尔逊相关系数分析特征之间的相关性
house.corr(method='pearson')
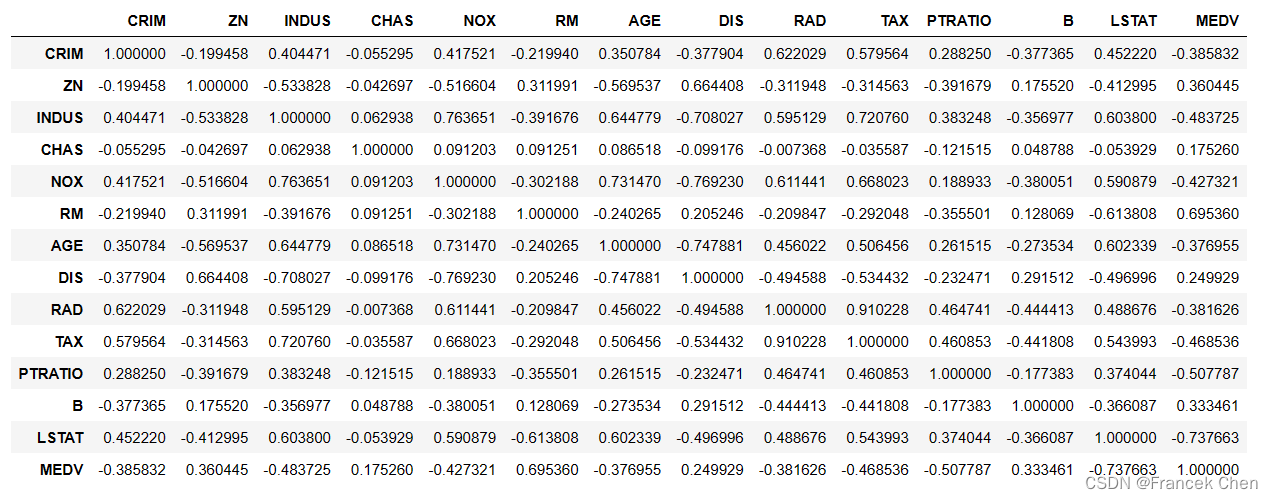
三、可视化不同特征与因变量’MEDV’(房价中值)间的相关性
#可视化不同特征与因变量'MEDV'(房价中值)间的相关性
fig = plt.figure( figsize=(8, 8), dpi=100 )
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falseplt.subplots_adjust(hspace=0.35)
plt.subplot(2, 2, 1)
#s指定点的大小,可用help(plt.scatter)查看帮助
plt.scatter(house['RM'], house['MEDV'], s=1, marker='o', label='RM-MEDV')
plt.xlabel( r"房间数 - $RM$" )
plt.ylabel( r"房价 - $MEDV$" )
plt.title(r"$\rho=0.695360$")plt.subplot(2, 2, 2)
plt.scatter(house['LSTAT'], house['MEDV'], s=1, marker='o', label='LSTAT-MEDV')
plt.xlabel( r"低层人口比例 - $LSTAT$" )
plt.title(r"$\rho=-0.737663$")plt.subplot(2, 2, 3)
plt.scatter(house['DIS'], house['MEDV'], s=1, marker='o', label='DIS-MEDV')
plt.xlabel( r"距就业中心距离 - $DIS$" )
plt.ylabel( r"房价 - $MEDV$" )
plt.title(r"$\rho=0.249929$")plt.subplot(2, 2, 4)
plt.scatter(house['CHAS'], house['MEDV'], s=1, marker='o', label='CHAS-MEDV')
plt.xlabel( r"河景房 - $CHAS$" )
plt.title(r"$\rho=0.175260$")
plt.show()
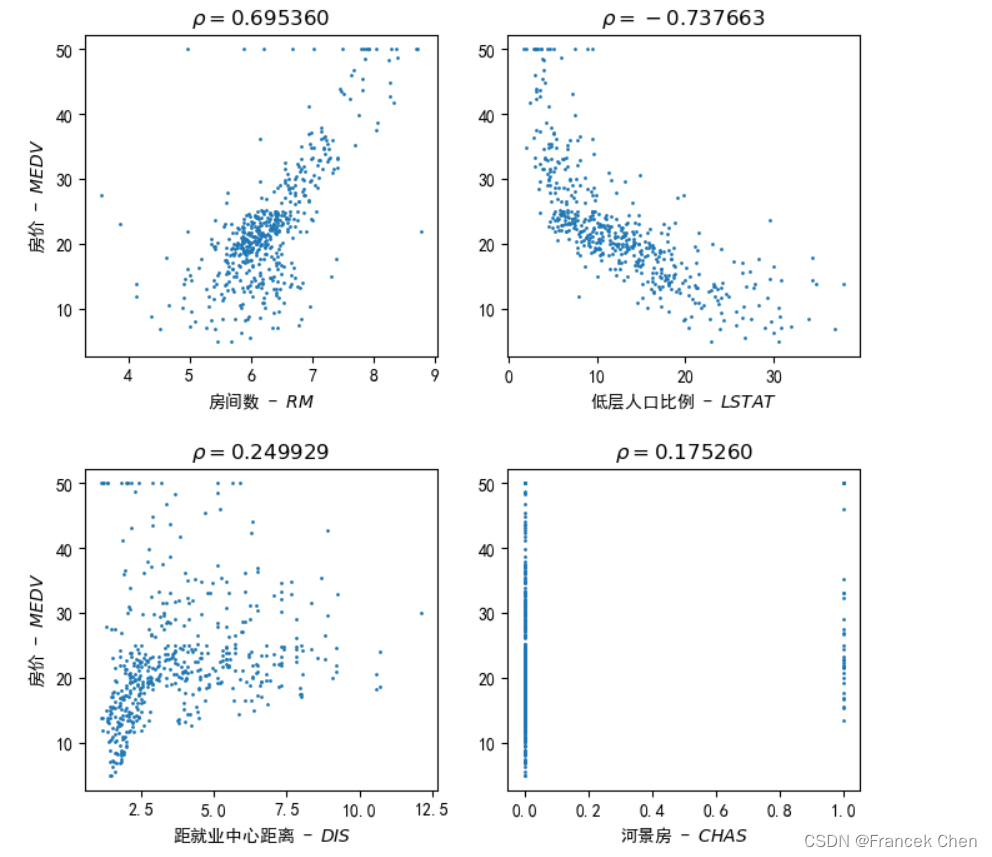
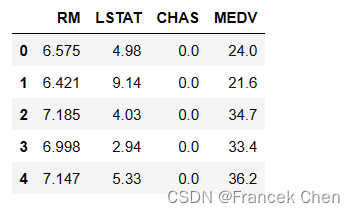
选取特征’RM’(房间数),‘LSTAT’(低层人口比例),‘CHAS’(河景房)和目标’MEDV’(房价中值)形成样本数据。
house1 = house[['RM','LSTAT','CHAS','MEDV']]
house1[:5]
如有必要,对数值型特征进行标准化。
在标准化之前,要使用MinMaxScaler进行特征缩放,这是一个常用的预处理步骤,有助于将数据缩放到一个指定的范围内,通常是[0,1]。
from sklearn.preprocessing import MinMaxScaler
mmScaler = MinMaxScaler() #创建MinMaxScaler对象mmScaler.fit(house1[['RM','LSTAT']]) #对MinMaxScaler对象进行拟合,以便获取特征的最小值和最大值
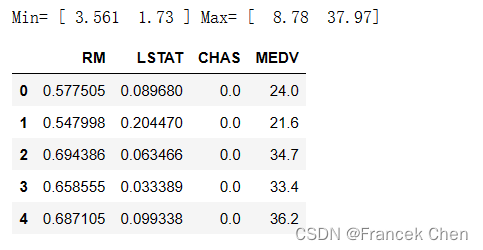
print("Min=", mmScaler.data_min_, "Max=", mmScaler.data_max_)m = mmScaler.transform(house1[['RM','LSTAT']]) #使用拟合好的MinMaxScaler对象对数据集进行特征缩放
# m = mmScaler.fit_transform(house1[['RM','LSTAT']])
# 创建一个DataFrame来存储特征缩放后的数据,同时保留原始特征'CHAS'和目标变量'MEDV'
house2m = pd.DataFrame(m, columns=['RM','LSTAT'])
house2m[['CHAS','MEDV']] = house1[['CHAS','MEDV']]
house2m[:5]
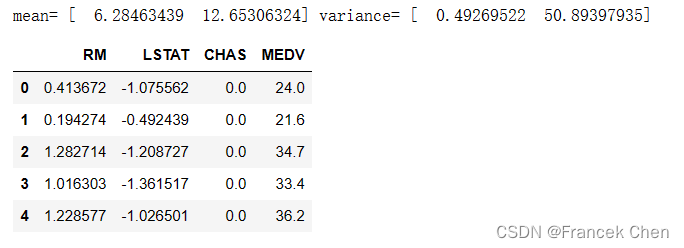
使用 scikit-learn 中的StandardScaler对数据集中的特征进行标准化处理。首先,使用fit方法将标准化器适配到数据上,并打印出了每个特征的均值和方差。然后,使用transform方法对数据进行转换,将标准化后的数据保存到变量z中。接着,将标准化后的特征数据与原始数据集中的其他列(比如CHAS和MEDV)一起合并到新的DataFrame house2z中。
from sklearn.preprocessing import StandardScaler
zScaler = StandardScaler() #创建一个StandardScaler对象
zScaler.fit(house1[['RM','LSTAT']]) #使用fit方法将StandardScaler对象适配到房屋数据的'RM'和'LSTAT'特征上,并计算它们的均值和方差
print("mean=", zScaler.mean_, "variance=", zScaler.var_)z = zScaler.transform(house1[['RM','LSTAT']]) #使用标准化器对'RM'和'LSTAT'特征进行标准化处理,并保存到变量z中
# z = zScaler.fit_transform(house1[['RM','LSTAT']])
# 创建一个新的DataFrame 'house2z'来保存标准化后的特征数据,并将'CHAS'和'MEDV'列添加到其中
house2z = pd.DataFrame(z, columns=['RM','LSTAT'])
house2z[['CHAS','MEDV']] = house1[['CHAS','MEDV']]
house2z[:5]
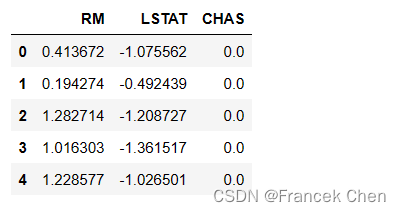
X = house2z[['RM','LSTAT','CHAS']]
X[:5]
Y = house2z['MEDV']
Y[:5]

四、划分训练集和测试集并进行回归分析
1、划分训练集和测试集
使用train_test_split()函数用于按一定比例划分训练集和测试集。
from sklearn.model_selection import train_test_split
# X为特征数据,Y为目标数据
# test_size参数指定测试集的比例,这里设置为0.2表示测试集占总数据集的20%
# random_state参数用于设置随机种子,相同的值得到相同的训练集和测试集划分
X_train,X_test,Y_train,Y_test = train_test_split(X, Y, test_size=0.2, random_state=2020)
# 打印训练集和测试集的形状(样本数,特征数或目标数)
print("X_train:", X_train.shape, "Y_train:", Y_train.shape)
print("X_test:", X_test.shape, "Y_test:", Y_test.shape)

#help(train_test_split)
2、创建一个线性回归模型并拟合训练数据
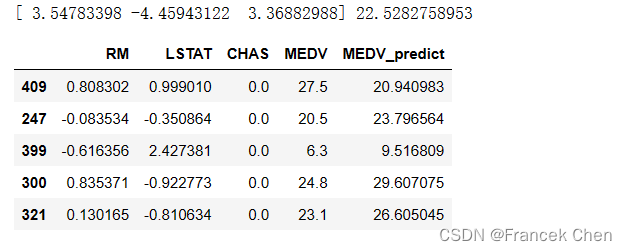
lr.coef_ 是模型的系数,lr.intercept_ 是模型的截距。接下来,将测试数据集的前五个样本用于预测,并将预测结果与实际值一起打印出来。这样可以比较模型的预测效果。
from sklearn.linear_model import LinearRegression
#创建LinearRegression估计器对象
lr = LinearRegression()
lr.fit(X_train, Y_train)
print(lr.coef_, lr.intercept_)XY_test = X_test[:5].copy()
XY_test['MEDV'] = Y_test[:5]
XY_test['MEDV_predict'] = lr.predict(X_test[:5])
XY_test
3、创建线性回归模型并用训练集数据进行拟合
接下来,计算训练集和测试集上的R方值(决定系数)和均方误差(MSE)来评估模型的性能。R方值越接近1,表示模型拟合得越好;而均方误差越小,表示模型的预测结果与实际值之间的偏差越小。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_errorlr = LinearRegression()
lr.fit(X_train, Y_train); print(lr.coef_, lr.intercept_)print("训练集R方:%f," % lr.score(X_train, Y_train), end='')
print("训练集MSE:%f" % mean_squared_error( Y_train, lr.predict(X_train)))print("测试集R方:%f," % lr.score(X_test, Y_test), end='')
print("测试集MSE:%f" % mean_squared_error( Y_test, lr.predict(X_test)))

#help(lr.score)
#help(mean_squared_error)
4、使用K折交叉验证来评估线性回归模型的性能
在每个折叠中,数据被分成训练集和测试集,模型在训练集上进行拟合,并在测试集上进行评估。这有助于更准确地评估模型的泛化能力。在每次迭代中,打印了训练集和测试集的索引,拟合模型的系数和截距,以及模型在测试集上的R方值和均方误差。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lr = LinearRegression()from sklearn.model_selection import KFold
kf = KFold(n_splits=3); n = 0
for train_index, test_index in kf.split(X):n += 1print(n, ":TRAIN", train_index.shape, " TEST", test_index.shape)X1_train, X1_test = X.iloc[train_index], X.iloc[test_index]Y1_train, Y1_test = Y.iloc[train_index], Y.iloc[test_index]lr.fit(X1_train, Y1_train); print(lr.coef_, lr.intercept_)print("测试集R方:%f," % lr.score(X1_test, Y1_test), end='')print("测试集MSE:%f" % mean_squared_error( Y1_test, lr.predict(X1_test)))

使用带有随机重排和指定随机种子的K折交叉验证来评估线性回归模型。在每个折叠中,将数据分为训练集和测试集,并在训练集上拟合模型。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lr = LinearRegression()
coef = [0, 0, 0]; intercept = 0from sklearn.model_selection import KFold
kf = KFold(n_splits=3, shuffle=True, random_state=2020); n = 0
for train_index, test_index in kf.split(X):n += 1X1_train, X1_test = X.iloc[train_index], X.iloc[test_index]Y1_train, Y1_test = Y.iloc[train_index], Y.iloc[test_index]lr.fit(X1_train, Y1_train)coef += lr.coef_; intercept += lr.intercept_lr.coef_ = coef/n; lr.intercept_ = intercept/n
print(lr.coef_, lr.intercept_)print("训练集R方:%f," % lr.score(X_train, Y_train), end='')
print("训练集MSE:%f" % mean_squared_error( Y_train, lr.predict(X_train)))print("测试集R方:%f," % lr.score(X_test, Y_test), end='')
print("测试集MSE:%f" % mean_squared_error( Y_test, lr.predict(X_test)))

5、使用岭回归模型(Ridge)来拟合数据
使用岭回归模型(Ridge)来拟合数据,并计算了模型在训练集和测试集上的R方和均方误差(MSE)。岭回归是一种常见的线性回归的正则化方法,通过引入L2范数惩罚项来控制模型的复杂度,有助于解决特征多重共线性问题。
设置alpha参数为1.0,这是岭回归中控制正则化强度的参数。较大的alpha值意味着更强的正则化。打印岭回归模型的系数(coef)和截距(intercept),以及在训练集和测试集上的R方和MSE。
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_errorrd = Ridge(alpha=1.0)
rd.fit(X_train, Y_train)
print(rd.coef_, rd.intercept_)print("训练集R方:%f," % rd.score(X_train, Y_train), end='')
print("训练集MSE:%f" % mean_squared_error( Y_train, rd.predict(X_train)))print("测试集R方:%f," % rd.score(X_test, Y_test), end='')
print("测试集MSE:%f" % mean_squared_error( Y_test, rd.predict(X_test)))

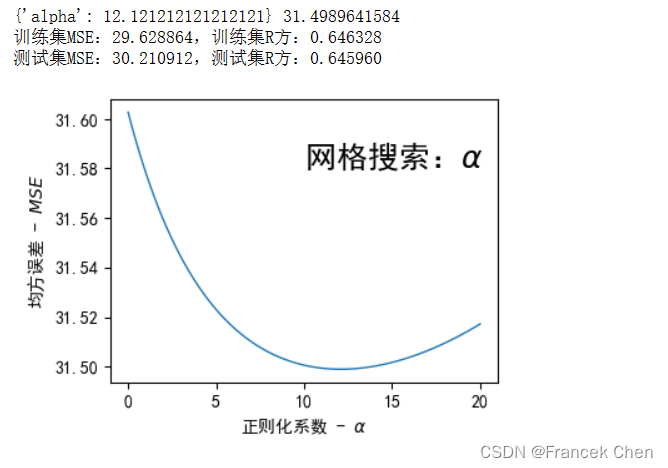
使用网格搜索(GridSearchCV)来对岭回归(Ridge)模型的正则化参数alpha进行优化,并绘制了正则化系数与交叉验证的均方误差(MSE)之间的关系。
- 使用
GridSearchCV来搜索不同的alpha值,并选出导致最低均方误差的最佳参数。 - 指定
lamda = np.linspace(0, 20, 100)作为网格搜索的候选参数范围。 scoring='neg_mean_squared_error'表示用负均方误差作为评分标准。cv=3表示使用3折交叉验证来评估每个alpha值的表现。
还计算了最佳参数对应的训练集和测试集上的R方(r2_score)和均方误差(neg_mean_squared_error)。最后,用一幅图展示了不同alpha值对应的交叉验证均方误差,以便直观地了解正则化强度与模型表现之间的关系。
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score
rd = Ridge()from sklearn.model_selection import GridSearchCV
lamda = np.linspace(0, 20, 100)
grid = {'alpha': lamda}
gs = GridSearchCV(estimator=rd, param_grid=grid,\scoring='neg_mean_squared_error', cv=3)
gs.fit(X_train, Y_train)
print(gs.best_params_, -gs.best_score_)
print("训练集MSE:%f," % -gs.score(X_train, Y_train), end='')
print("训练集R方:%f" % r2_score( Y_train, gs.predict(X_train)))
print("测试集MSE:%f," % -gs.score(X_test, Y_test), end='')
print("测试集R方:%f" % r2_score( Y_test, gs.predict(X_test)))fig = plt.figure( figsize=(4, 3), dpi=100 )
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.plot(lamda, -gs.cv_results_['mean_test_score'], linewidth=1)
plt.text(10, 31.58, r"网格搜索:$\alpha$", fontsize=18)
plt.xlabel( r"正则化系数 - $\alpha$" )
plt.ylabel( r"均方误差 - $MSE$" )
plt.show()
6、使用Lasso回归防止过拟合
使用了Lasso回归模型,该模型是线性回归的变体,带有L1正则化项。Lasso回归通过缩小回归系数的绝对值来防止过拟合,最终可能导致一些系数变为零,从而实现特征选择的效果。
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error
# 创建了一个Lasso模型,正则化参数alpha=1.0,最大迭代次数max_iter=1000
las = Lasso(alpha=1.0, max_iter=1000)
las.fit(X_train, Y_train)
print(las.coef_, las.intercept_) #训练模型后,输出模型的系数和截距
# 计算训练集和测试集上的R方(score方法)和均方误差(mean_squared_error)
print("训练集R方:%f," % las.score(X_train, Y_train), end='')
print("训练集MSE:%f" % mean_squared_error( Y_train, las.predict(X_train)))print("测试集R方:%f," % las.score(X_test, Y_test), end='')
print("测试集MSE:%f" % mean_squared_error( Y_test, las.predict(X_test)))

多项式特征扩展与Lasso回归结合。
PolynomialFeatures:这个类用于生成多项式特征,它将输入特征的所有可能的组合作为新的特征。在这里,使用PolynomialFeatures(2, include_bias=False)创建了一个二次多项式特征扩展对象,并将其应用于训练集和测试集,得到了扩展后的特征矩阵X_train_pf和X_test_pf。Lasso:这是Lasso回归模型的调用,使用默认参数alpha=1.0和max_iter=1000。然后,使用扩展后的特征矩阵X_train_pf对模型进行拟合。- 输出模型系数和截距:打印了模型的系数和截距,这些系数对应于扩展后的特征空间中的每个特征。
- 训练集和测试集上的评估:最后,分别计算了训练集和测试集上的R方值和均方误差。R方值(决定系数)用于评估模型对目标变量的拟合程度,均方误差则衡量了模型的预测误差大小。
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeaturespoly = PolynomialFeatures(2, include_bias=False)
X_train_pf = poly.fit_transform(X_train)
X_test_pf = poly.fit_transform(X_test)
# X_train的形状是(样本数, 特征数),而X_train_pf的形状是(样本数, 扩展后的特征数)
print("X_train:", X_train.shape, ",X_train_pf.shape:", X_train_pf.shape)las = Lasso(alpha=1.0, max_iter=1000)
las.fit(X_train_pf, Y_train)
print(las.coef_, las.intercept_) #模型的系数和截距
# 训练集和测试集上的R方值和均方误差
print("训练集R方:%f," % las.score(X_train_pf, Y_train), end='')
print("训练集MSE:%f" % mean_squared_error(Y_train, las.predict(X_train_pf)))print("测试集R方:%f," % las.score(X_test_pf, Y_test), end='')
print("测试集MSE:%f" % mean_squared_error(Y_test, las.predict(X_test_pf)))

相关文章:

【机器学习与实现】线性回归示例——波士顿房价分析
目录 一、创建Pandas对象并查看数据的基本情况二、使用皮尔逊相关系数分析特征之间的相关性三、可视化不同特征与因变量MEDV(房价中值)间的相关性四、划分训练集和测试集并进行回归分析 一、创建Pandas对象并查看数据的基本情况 boston.csv数据集下载&a…...

Redis核心数据结构——跳表(生成数据到文件和从文件中读取数据、模块合并、)
生成文件和从文件中读取数据。 需求如下: 你的任务是实现 SkipList 类中的数据持久化成员函数和数据加载成员函数。 持久化数据成员函数签名:void dump_file(); 该成员函数负责将存储引擎内的数据持久化到文件中。数据的持久化格式是将每个键值对写入文…...

微信小程序下载文件详解
在微信小程序中,下载文件通常涉及使用 wx.downloadFile API。这个 API 可以将网络资源下载到本地临时文件路径,然后你可以使用 wx.saveFile 将临时文件保存到本地持久存储位置。下面是一个下载文件的详细过程: 使用 wx.downloadFile 下载文件…...

2024 概率论和数理统计/专业考试/本科考研/论文/重点公式考点汇总
## 列表http://www.deepnlp.org/equation/category/statistics ## 均匀分布http://www.deepnlp.org/equation/uniform-distribution ## t-分布http://www.deepnlp.org/equation/student-t-distribution ## 伯努利分布http://www.deepnlp.org/equation/bernoulli-distributio…...

四川易点慧电子商务抖音小店:潜力无限的新零售风口
在当今数字化浪潮中,电子商务已经成为推动经济发展的重要引擎。四川易点慧电子商务有限公司凭借其敏锐的市场洞察力和创新精神,成功在抖音小店这一新兴平台上开辟出一片新天地。本文将探讨四川易点慧电子商务抖音小店的潜力及其在新零售领域的影响力。 一…...

Seal^_^【送书活动第3期】——《Hadoop大数据分析技术》
Seal^_^【送书活动第3期】——《Hadoop大数据分析技术》 一、参与方式二、作者荐语三、图书简介四、本期推荐图书4.1 前 言4.2 本书内容4.3 本书目的4.4 本书适合的读者4.5 配套源码、PPT课件等资源下载 五、目 录六、🛒 链接直达 Hadoop框架入门书,可当…...
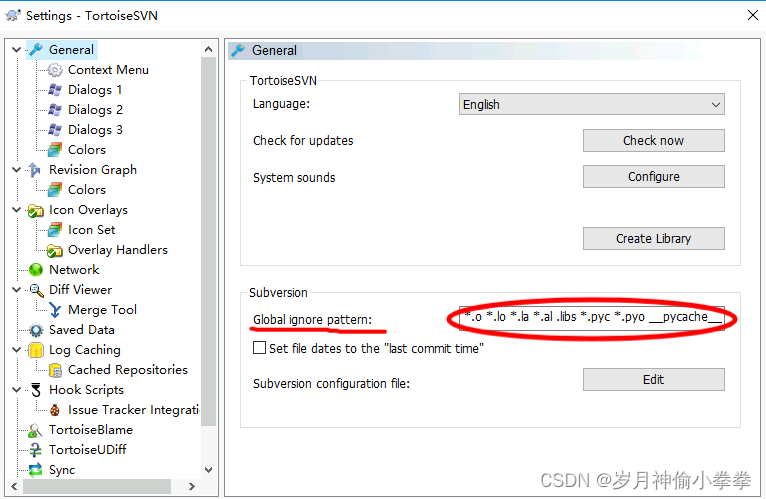
win10下,svn上传.so文件失败
问题:win10下使用TortoiseSVN,svn上传.so文件失败 解决:右键,选择Settings,Global ignore pattern中删除*.so,保存即可。...
ubuntu20安装colmap
系统环境 ubuntu20 ,cuda11.8 ,也安装了anaconda。因为根据colmap的官方文档说的,如果根据apt-get安装的话,默认是非cuda版本的,而我觉得既然都安装了cuda11.8了,自然也要安装cuda版本的colmap。 安装步骤…...
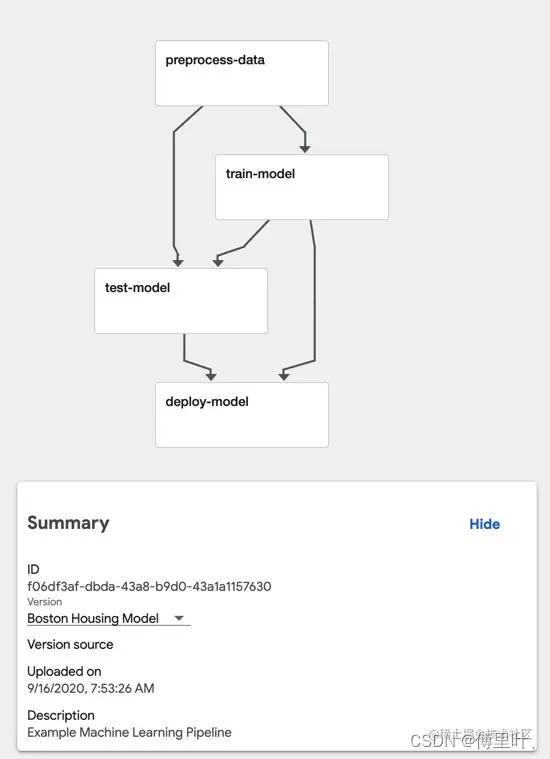
kubeflow简单记录
kubeflow 13.7k star 1、Training Operator 包括PytorchJob和XGboostJob,支持部署pytorch的分布式训练 2、KFServing快捷的部署推理服务 3、Jupyter Notebook 基于Web的交互式工具 4、Katib做超参数优化 5、Pipeline 基于Argo Workflow提供机器学习流程的创建、编排…...

ARM的工作模式
ARM处理器设计有七种工作模式,这些模式允许处理器在不同的情境下以不同的权限级别执行任务,下面是这七大工作模式的概述: 用户模式(User,USR): 这是非特权模式,大多数应用程序在此…...
为家庭公网IP配置DDNS域名
文章目录 域名配置域名更新frp配置修改 在成功完成frp改造Windows笔记本实现家庭版免费内网穿透之后,某天我突然发现内网穿透失效了,一番排查之后原来是路由器对应的公网IP更换了。果然我分到的并不是固定的公网IP,而是会定期变化的。为了免受…...

QT-TCP通信
网上的资料太过于书面化,所以看起来有的让人云里雾里,看不懂C-tcpsockt和S-tcpsocket的关系 所以我稍微画了一下草图帮助大家理解两个套接字之间的关系。字迹有的飘逸勉强看看 下面是代码 服务端: MainWindow::MainWindow(QWidget *parent) …...

SparkSQL优化
SparkSQL优化 优化说明 缓存数据到内存 Spark SQL可以通过调用spark.sqlContext.cacheTable("tableName") 或者dataFrame.cache(),将表用一种柱状格式( an inmemory columnar format)缓存至内存中。然后Spark SQL在执行查询任务…...
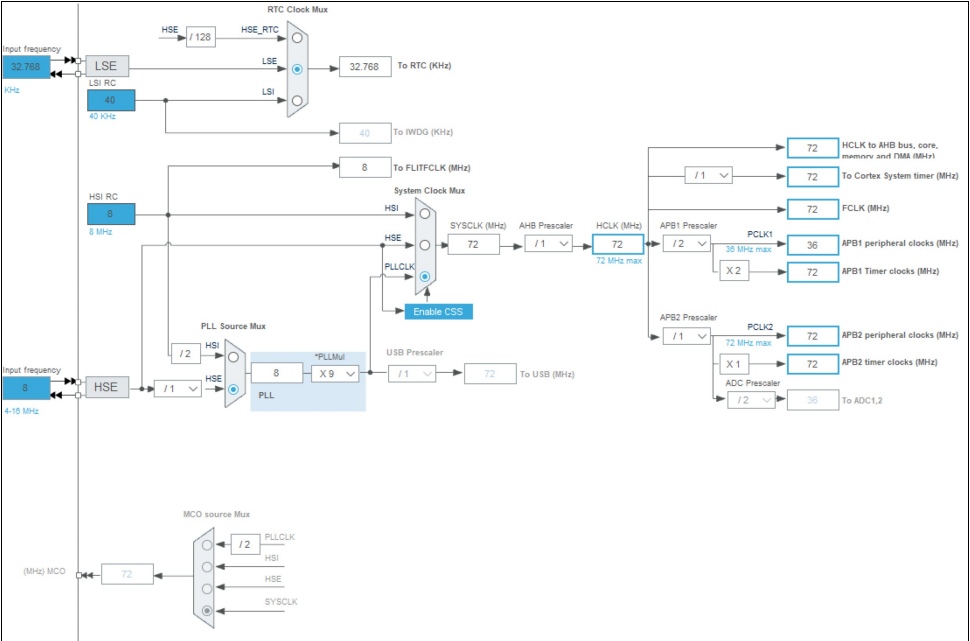
STM32——基础篇
技术笔记! 一、初识STM32 1.1 ARM内核系列 A 系列:Application缩写。高性能应用,比如:手机、电脑、电视等。 R 系列:Real-time缩写。实时性强,汽车电子、军工、无线基带等。 M 系列:Microcont…...
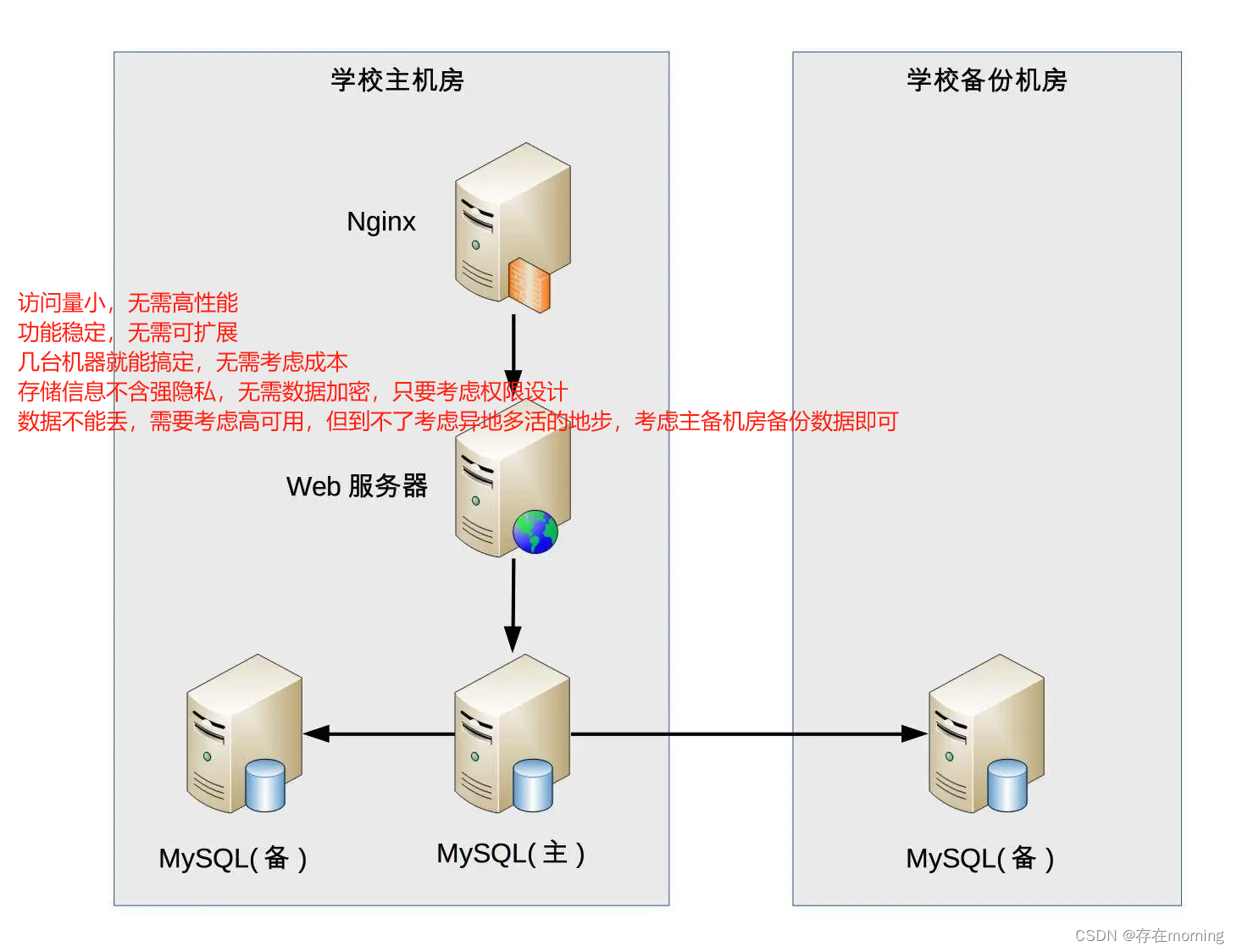
【从零开始学架构 架构基础】架构设计的本质、历史背景和目的
本文是《从零开始学架构》的第一篇学习笔记,主要理解架构的设计的本质定义、历史背景以及目的。 架构设计的本质 分别从三组概念的区别来理解架构设计。 系统与子系统 什么是系统,系统泛指由一群有关联的个体组成,根据某种规则运作&#…...

Learning C# Programming with Unity 3D
作者:Alex Okita 源码地址:GitHub - badkangaroo/UnityProjects: A repo for all of the projects found in the book. 全书 686 页。...

北京车展现场体验商汤DriveAGI自动驾驶大模型展现认知驱动新境界
在2024年北京国际汽车展的舞台上,众多国产车型纷纷亮相,各自展示着独特的魅力。其中,小米SUV7以其精美的外观设计和宽敞的车内空间,吸引了无数目光,成为本届车展上当之无愧的明星。然而,车辆的魅力并不仅限…...
企业终端安全管理软件有哪些?终端安全管理软件哪个好?
终端安全的重要性大家众所周知,关系到生死存亡的东西。 各类终端安全管理软件应运而生,为企业提供全方位、多层次的终端防护。 有哪些企业终端安全管理软件? 一、主流企业终端安全管理软件 1. 域智盾 域智盾是一款专为企业打造的全面终端…...
媒体驱动框架整理--HDMI框架(2))
Linux内核--设备驱动(七)媒体驱动框架整理--HDMI框架(2)
目录 一、引言 二、drm框架 ------>2.1、画布( FrameBuffer ) ------>2.2、绘图现场(CRTC) ------>2.3、输出转换器(Encoder ) ------>2.4、连接器 (Connector ) ------>2.5、显示面(Planner) 三、VOP部分详解 ------>3.1、dts ------>3.2、v…...

3.3 Gateway之自定义过滤器
1.Gateway过滤器种类 过滤器种类描述GatewayFilter路由过滤器,作用于任意指定的路由。默认不生效,要配置到路由后生效GlobalFilter全局过滤器,作用范围是所有路由。声明后自定生效 2.Gateway过滤器参数 参数描述ServerWebExchangeGateway内…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
【QT控件】显示类控件
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏:QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...
