面试经典150题——三数之和
面试经典150题 day29
- 题目来源
- 我的题解
- 方法一 暴力解法 超时
- 方法二 扩展两数之和(双指针)
- 方法三 扩展为通用的n数之和
题目来源
力扣每日一题;题序:15
我的题解
方法一 暴力解法 超时
进行三重循环遍历,判断和是否为0,若为0,则将对应的值组合成List并加入Set。
时间复杂度:O( n 3 n^3 n3)
空间复杂度:O(n)
public List<List<Integer>> threeSum(int[] nums) {Set<List<Integer>> resSet=new HashSet<>();int n=nums.length;for(int i=0;i<n-2;i++){for(int j=i+1;j<n-1;j++){for(int k=j+1;k<n;k++){if(nums[i]+nums[j]+nums[k]==0){List<Integer> t=Arrays.asList(nums[i],nums[j],nums[k]);t.sort((a,b)->a-b);resSet.add(t);}}}}return new ArrayList<>(resSet);
}
方法二 扩展两数之和(双指针)
先确定一个数,然后使用两数之和的解法进行计算。注意需要去重,即在求两数之和的过程中需要将去掉重复的元素。
时间复杂度:O( n 2 n^2 n2)。
空间复杂度:O(n)
public List<List<Integer>> threeSum(int[] nums) {Arrays.sort(nums);List<List<Integer>> res=new ArrayList<>();for(int i=0;i<nums.length;){List<List<Integer>> t=twoSum(nums,-nums[i],i);int pre=nums[i];while(i<nums.length&&nums[i]==pre)i++;res.addAll(t);}return res;
}
public List<List<Integer>> twoSum(int[] nums,int target,int index){int left=index+1,right=nums.length-1;List<List<Integer>> res=new ArrayList<>();while(left<right){int tNum=nums[left]+nums[right];int preLeft=nums[left];int preRight=nums[right];if(index==left){left++;continue;}if(index==right){right--;continue;}if(tNum==target){List<Integer> t=Arrays.asList(-target,nums[left],nums[right]);res.add(t);while(left<right&&nums[left]==preLeft)left++;while(right>left&&nums[right]==preRight)right--;}else if(tNum<target){while(left<right&&nums[left]==preLeft)left++;}else{while(right>left&&nums[right]==preRight)right--;}}return res;
}
方法三 扩展为通用的n数之和
时间复杂度:O( n 2 n^2 n2)。
空间复杂度:O(n)
public List<List<Integer>> threeSum(int[] nums) {Arrays.sort(nums);List<List<Integer>> resList = nSum(nums, 0, 3, 0);return resList;
}public List<List<Integer>> nSum(int[] nums, int target, int n, int start) {int len = nums.length;List<List<Integer>> res = new ArrayList<>();if (n == 2) {int left = start, right = len - 1;while (left < right) {int temp = nums[left] + nums[right];int l = nums[left], r = nums[right];if (temp < target) {while (left < right && l == nums[left])left++;} else if (temp > target) {while (left < right && r == nums[right])right--;} else {List<Integer> sub = new ArrayList(Arrays.asList(nums[left], nums[right]));res.add(sub);while (left < right && l == nums[left])left++;while (left < right && r == nums[right])right--;}}} else {for (int i = start; i < len; i++) {List<List<Integer>> subList = nSum(nums, target - nums[i], n - 1, i + 1);for (List<Integer> list : subList) {list.add(nums[i]);res.add(list);}while (i < len - 1 && nums[i] == nums[i + 1])i++;}}return res;
}
有任何问题,欢迎评论区交流,欢迎评论区提供其它解题思路(代码),也可以点个赞支持一下作者哈😄~
相关文章:

面试经典150题——三数之和
面试经典150题 day29 题目来源我的题解方法一 暴力解法 超时方法二 扩展两数之和(双指针)方法三 扩展为通用的n数之和 题目来源 力扣每日一题;题序:15 我的题解 方法一 暴力解法 超时 进行三重循环遍历,判断和是否为…...

go动态创建/增加channel并处理数据
背景描述 有一个需求,大概可以描述为:有多个websocket连接,因此消息会并发地发送过来,这些消息中有一个标志可以表明是哪个连接发来的消息,但只有收到消息后才能建立channel或写入已有channel,在收消息前无…...
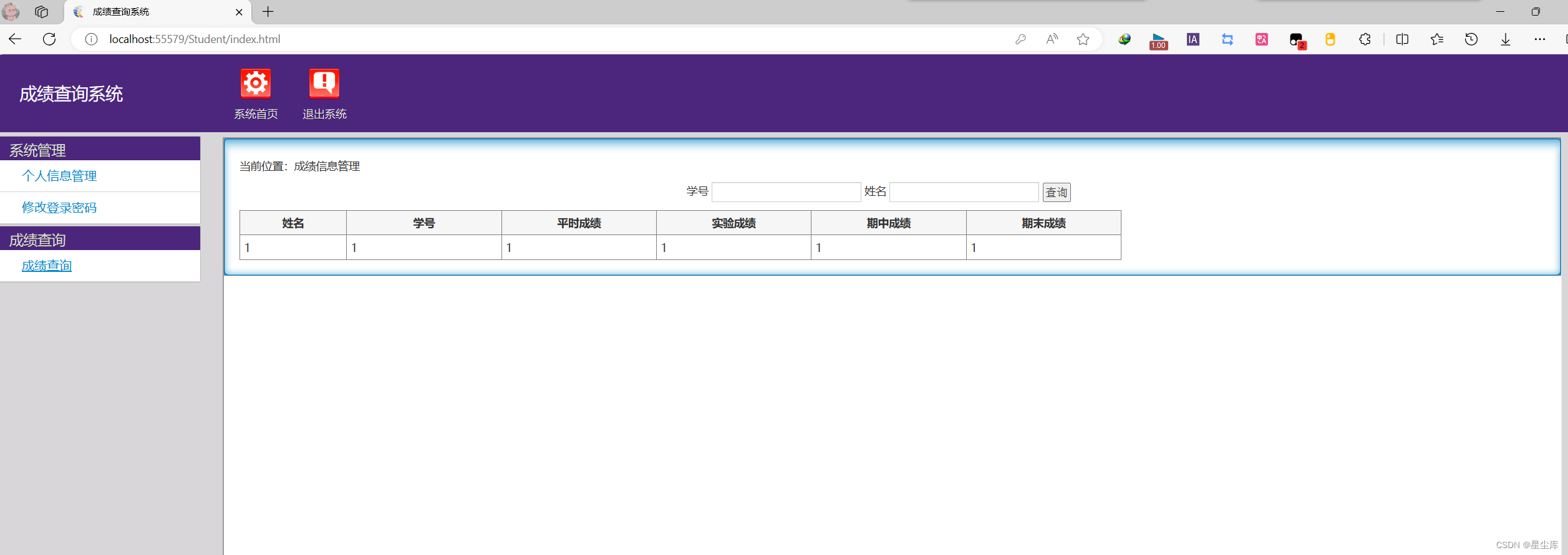
asp.net成绩查询系统
说明文档 运行前附加数据库.mdf(或sql生成数据库) 主要技术: 基于asp.net架构和sql server数据库 功能模块: asp.net成绩查询系统 学生功能有查看成绩和修改账号密码等 后台管理员可以进行用户管理 管理员添加管理员查询注…...

Express路由
什么是路由 官方定义:路由确定了应用程序如何响应客户端对特定端点的请求。 路由的使用 一个路由的组成有 请求方法、路径 和 回调函数 组成。 Express中提供了一些列方法,可以很方便的使用路由,使用格式如下: app.<metho…...

在做题中学习(53): 寻找旋转数组中的最小值
153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode) 解法:O(logn)->很可能就是二分查找 思路:再看看题目要求,可以画出旋转之后数组中元素的大小关系: 首先,数组是具有二段性的(适配二分查…...
 元组)
C#语言进阶(三) 元组
总目录 C# 语法总目录 元组目录 元组1. 元组元素命名2. 元组的解构3. 元组的比较 元组 元组(tuple)是一组存储值的便捷方式。 元组的目的主要是,不使用out参数而从方法中返回多个值。(匿名类型无法做这个操作)元组能做匿名类型所有操作。 元组是值类型࿰…...

实用的Chrome 浏览器命令
Google Chrome 浏览器提供了许多快捷命令和实用功能,可以帮助用户提高效率和改善浏览体验。这里列举了一些非常实用的Chrome浏览器命令: 1. **CtrlT** / **CmdT** - 打开一个新的标签页。 2. **CtrlShiftT** / **CmdShiftT** - 重新打开最后关闭的标签页…...
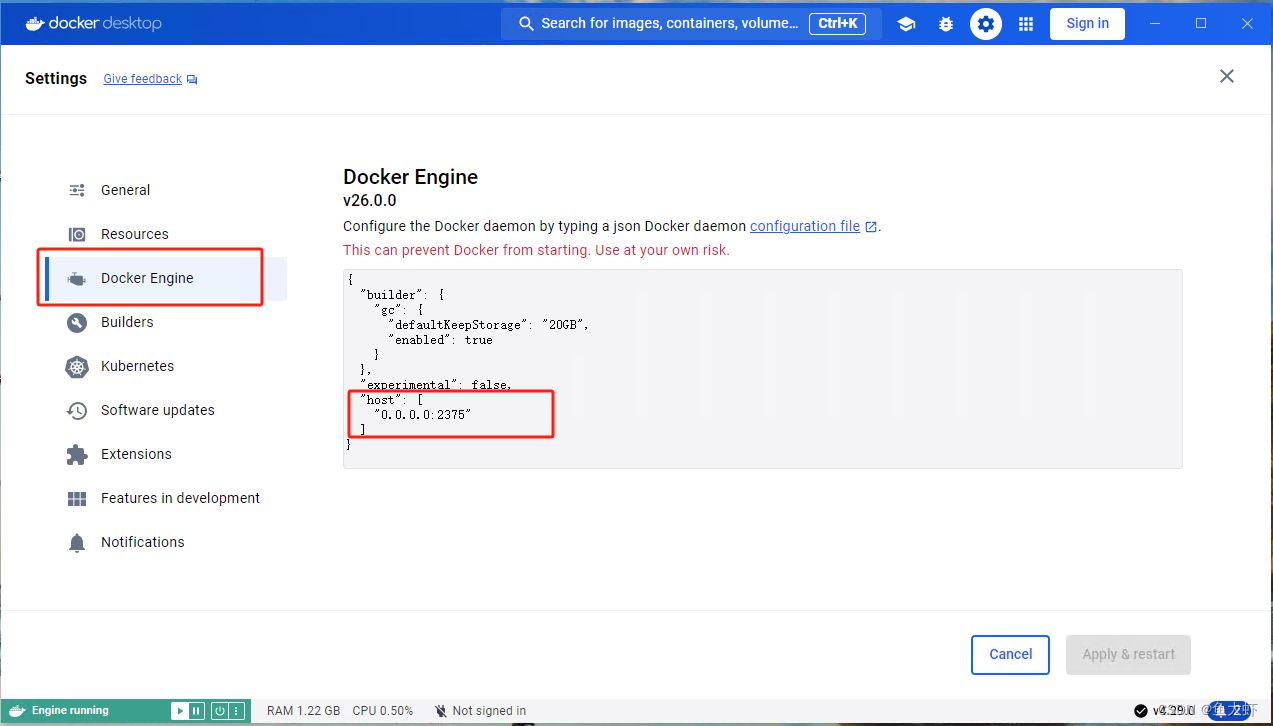
IDEA远程连接docker服务,windows版docker desktop
1.windows上安装docker desktop docker desktop下载地址:Docker Desktop: The #1 Containerization Tool for Developers | Docker 有的windows系统不支持安装docker desktop 安装完之后我们可以直接打开,可以选择不登录使用 我们用IDEA连接到docker …...

Rust 和 Go 哪个更好?
在讨论 Rust 与 Go 两种编程语言哪种更优秀时,我们将探讨它们在性能、简易性、安全性、功能、规模和并发处理等方面的比较。同时,我们看看它们有什么共同点和根本的差异。现在就来看看这个友好而公平的对比。 Rust 和 Go 都是优秀的选择 首先ÿ…...
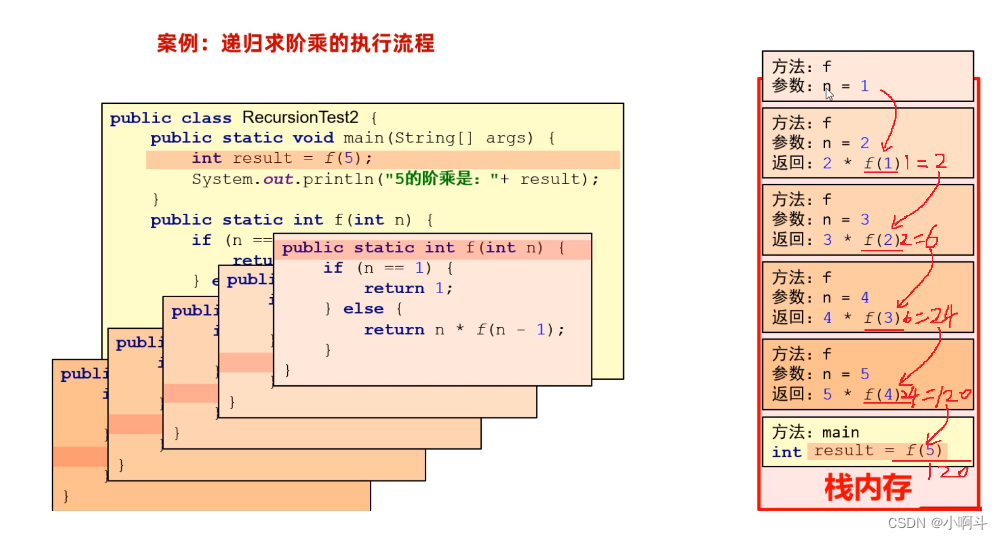
【免费Java系列】大家好 ,今天是学习面向对象高级的第八天点赞收藏关注,持续更新作品 !
这是java进阶课面向对象第一天的课程可以坐传送去学习http://t.csdnimg.cn/Lq3io day08-Map集合、Stream流、File类 一、Map集合 同学们,在前面几节课我们已经学习了Map集合的常用方法,以及遍历方式。 下面我们要学习的是Map接口下面的是三个实现类H…...

RPC 失败。curl 16 Error in the HTTP2 framing layer
报错: (base) hh-virtual-machine:~/work$ git clone https://github.com/yangzongzhuan/RuoYi-Vue3.git 正克隆到 RuoYi-Vue3... error: RPC 失败。curl 16 Error in the HTTP2 framing layer fatal: 在引用列表之后应该有一个 flush 包这个错误通常是由于 Git 在…...
(图论)最短路问题合集(包含C,C++,Java,Python,Go)
不存在负权边: 1.朴素dijkstra算法 原题: 思路:(依然是贪心的思想) 1.初始化距离:dis[1]0,dis[i]INF(正无穷) 2.循环n次: 找到当前不在s中的dis最小的点&…...
电脑文件批量重命名不求人:快速操作,高效技巧让你轻松搞定
在数字化时代,电脑文件的管理与整理显得尤为重要。当面对大量需要重命名的文件时,一个个手动修改不仅耗时,还容易出错。那么,有没有一种方法可以快速、高效地完成这一任务呢?答案是肯定的,下面就来介绍几种…...

基于springboot的网上点餐系统源码数据库
基于springboot的网上点餐系统源码数据库 随着科学技术的飞速发展,各行各业都在努力与现代先进技术接轨,通过科技手段提高自身的优势;对于网上点餐系统当然也不能排除在外,随着网络技术的不断成熟,带动了网上点餐系统…...
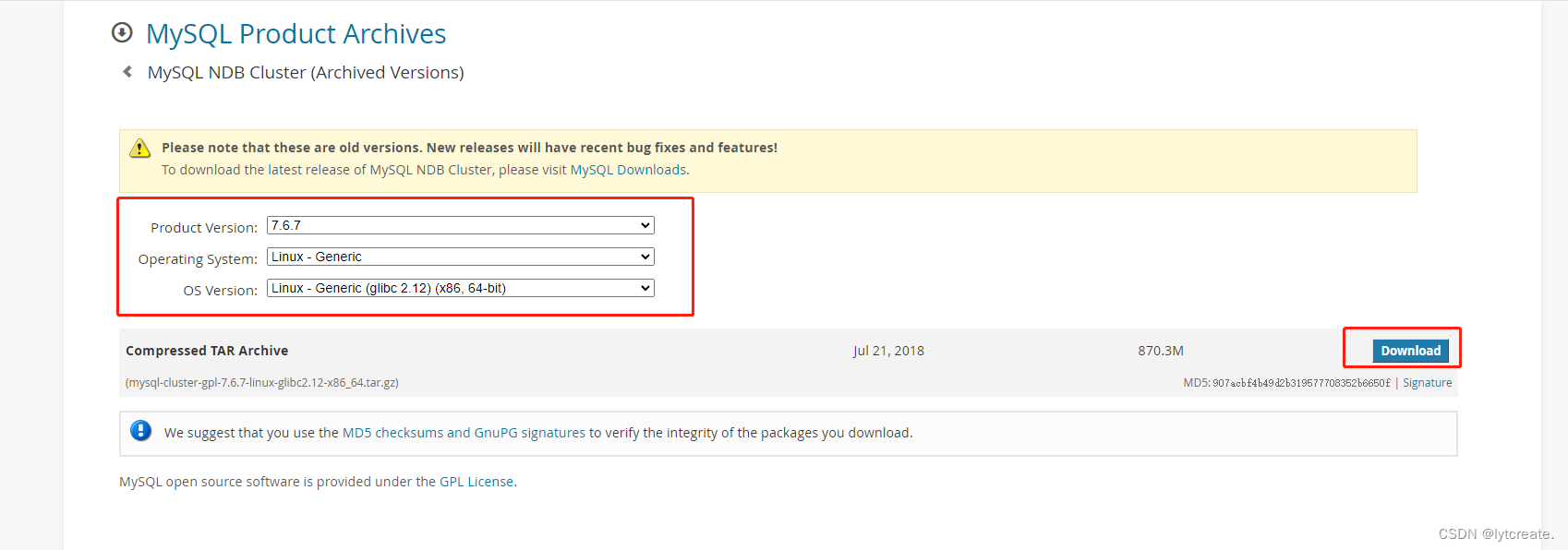
mysql cluster数据库集群介绍、部署及配置
前言: MySQL集群是一个无共享的、分布式节点架构的存储方案,旨在提供容错性和高性能。它由三个主要节点组成:管理节点(MGM)、数据节点和SQL节点。 管理节点(MGM) 定义与用途:管理节点是MySQL Cluster的控制中心,负责管理集群内的其他节点。它提供配置数据,启动和停止…...

uniapp的app端软件更新弹框
1:使用html PLUS实现:地址HTML5 API Reference (html5plus.org),效果图 2:在app.vue的onLaunch生命周期中,代码如下: onLaunch: function() {let a 0let view new plus.nativeObj.View(maskView, {backg…...
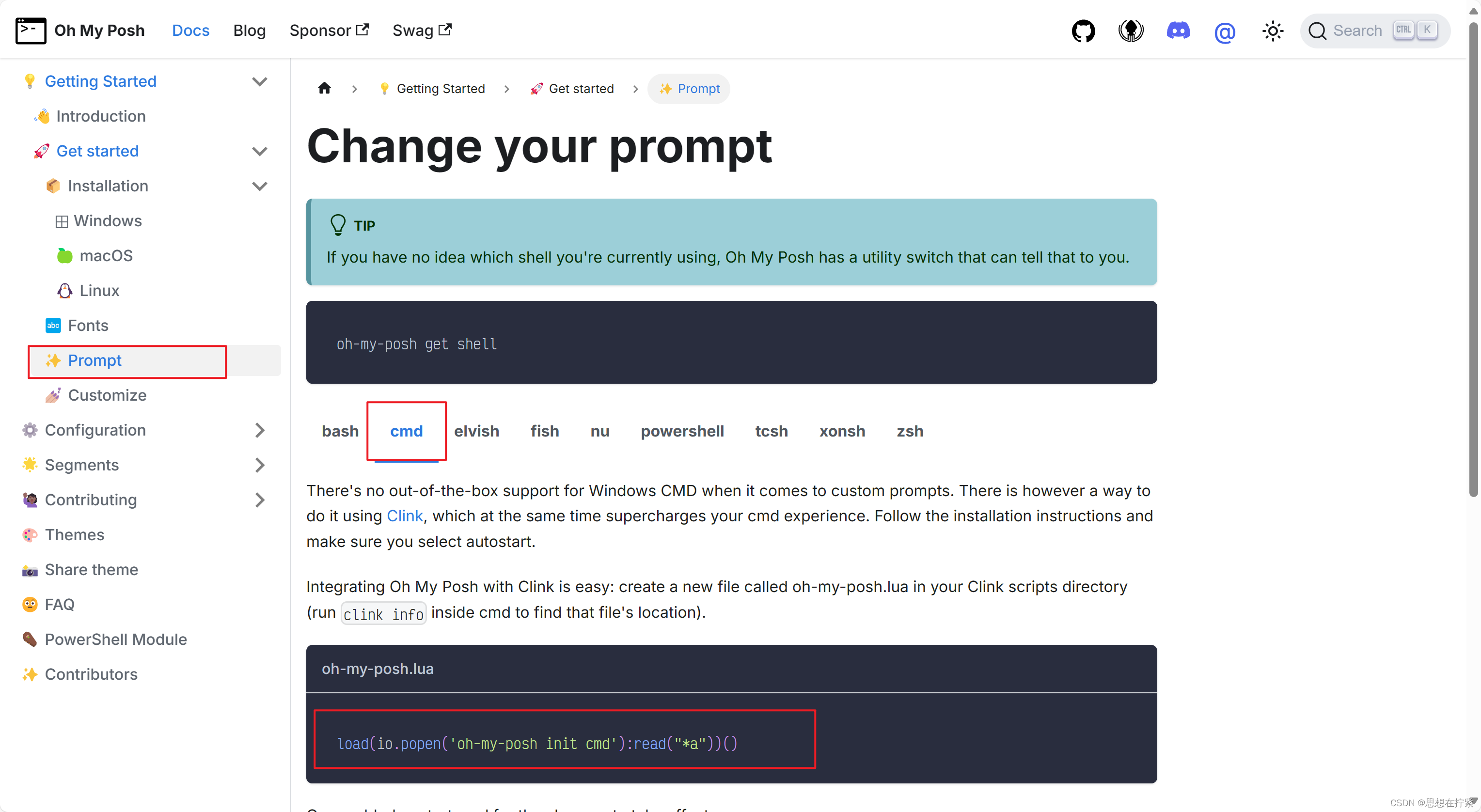
win11 Terminal 部分窗口美化
需求及分析:因为在 cmd、anaconda prompt 窗口中输入命令较多,而命令输入行和输出结果都是同一个颜色,不易阅读,故将需求定性为「美化窗口」。 美化结束后,我在想是否能不安装任何软件,简单地通过调整主题颜…...
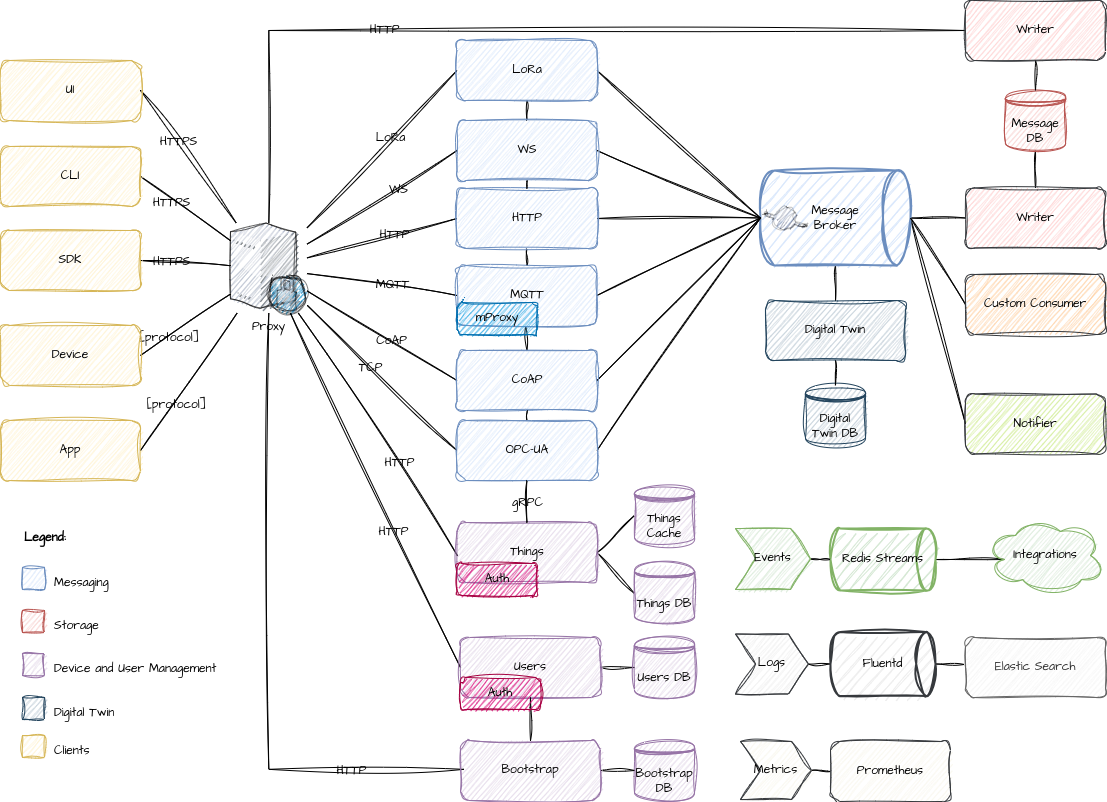
开源go实现的iot物联网新基建平台
软件介绍 Magistrala IoT平台是由Abstract Machines公司开发的创新基础设施解决方案,旨在帮助组织和开发者构建安全、可扩展和创新的物联网应用程序。曾经被称为Mainflux的平台,现在已经开源,并在国际物联网领域受到广泛关注。 功能描述 多协…...
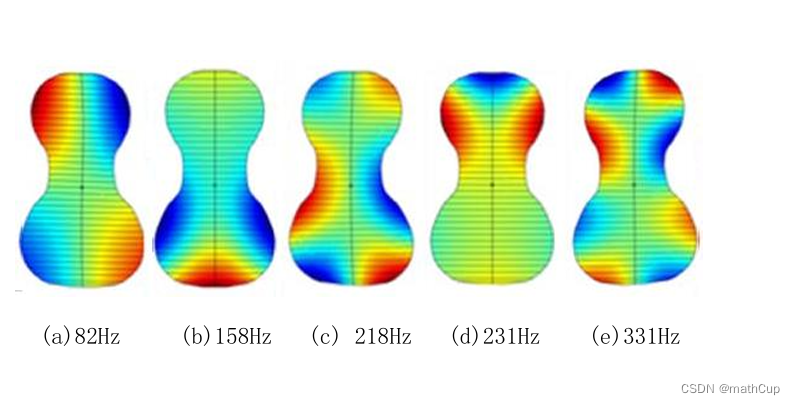
24深圳杯ABCD成品论文47页+各小问代码+图表
A题多个火箭残骸的准确定位: A题已经更新完22页完整版论文+高清无水印照片+Python(MATLAB)代码简单麦麦https://www.jdmm.cc/file/2710544/ 问题1:单个残骸的音爆位置确定 建模思路: 1. 声波传…...

doris经典bug
在部署完登录web页面查看的时候会发现只有一个节点可以读取信息剩余的节点什么也没读取到 在发现问题后,我们去对应的节点去看log日志,发现它自己绑定到前端的地址上了 现在我们已经发现问题了,以下就开始解决问题 重置doris 首先对be进行操…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
