高等数学——定积分和不定积分
文章目录
- 不定积分
- 概念
- 几何意义
- 性质
- 不定积分的基本公式
- 三种主要积分法
- 三类常见可积函数积分
- 定积分
- 概念
- 几何意义
- 性质
- 积分上限的函数
- 定积分的计算
- 几何应用
- 反常积分
- 无穷区间的反常积分
- 无界函数的反常积分
不定积分
不定积分是导数的逆运算。
概念
- 原函数:设f(x)f(x)f(x)在区间(a,b)(a,b)(a,b)内有定义,若存在函数F(x)F(x)F(x),使其在该区间内任何一点都有F′(x)=f(x)F'(x)=f(x)F′(x)=f(x),则称F(x)F(x)F(x)为f(x)f(x)f(x)在该区间内的原函数。若F(x)F(x)F(x)为f(x)f(x)f(x)在某区间内的原函数,则F(x)+CF(x)+CF(x)+C也为f(x)f(x)f(x)在该区间内的原函数。若F(x),G(x)F(x),G(x)F(x),G(x)为f(x)f(x)f(x)在某区间内的原函数,则F(x)−G(x)=CF(x)-G(x)=CF(x)−G(x)=C。
- 不定积分:f(x)f(x)f(x)的全体原函数称为f(x)f(x)f(x)的不定积分,记为∫f(x)dx\int f(x)dx∫f(x)dx,如果F(x)F(x)F(x)为f(x)f(x)f(x)的一个原函数,则有∫f(x)dx=F(x)+C\int f(x)dx=F(x)+C∫f(x)dx=F(x)+C。
- 原函数存在定理:若f(x)f(x)f(x)在区间III上连续,则f(x)f(x)f(x)在区间III上一定存在原函数;若f(x)f(x)f(x)在区间III上有第一类间断点,则f(x)f(x)f(x)在区间III上没有原函数。
几何意义
设F(x)F(x)F(x)为f(x)f(x)f(x)的一个原函数,则从几何上看,F(x)F(x)F(x)表示平面上的一条曲线,称为f(x)f(x)f(x)的积分曲线,因此不定积分∫f(x)dx=F(x)+C\int f(x)dx=F(x)+C∫f(x)dx=F(x)+C在几何上表示一簇积分曲线,这簇积分曲线对于横坐标xxx处的切线都相互平行。
性质
- (∫f(x)dx)′=f(x)(\int f(x)dx)'=f(x)(∫f(x)dx)′=f(x)
- d(∫f(x)dx)=f(x)dxd(\int f(x)dx)=f(x)dxd(∫f(x)dx)=f(x)dx
- ∫f′(x)dx=f(x)+C\int f'(x)dx=f(x)+C∫f′(x)dx=f(x)+C
- ∫df(x)=f(x)+C\int df(x)=f(x)+C∫df(x)=f(x)+C
- ∫[f(x)±g(x)]dx=∫f(x)dx±∫g(x)dx\int [f(x)\pm g(x)]dx=\int f(x)dx\pm \int g(x)dx∫[f(x)±g(x)]dx=∫f(x)dx±∫g(x)dx
- ∫kf(x)dx=k∫f(x)dx(k为常数)\int kf(x)dx=k\int f(x)dx(k为常数)∫kf(x)dx=k∫f(x)dx(k为常数)
不定积分的基本公式
- ∫0dx=C\int 0dx=C∫0dx=C
- ∫xadx=1a+1xa+1+C(a≠−1)\int x^adx=\frac{1}{a+1}x^{a+1}+C(a≠-1)∫xadx=a+11xa+1+C(a=−1)
- ∫1xdx=ln∣x∣+C\int \frac{1}{x}dx=ln|x|+C∫x1dx=ln∣x∣+C
- ∫axdx=axlna+C(a>0,a≠1)\int a^xdx=\frac{a^x}{lna}+C(a>0,a≠1)∫axdx=lnaax+C(a>0,a=1)
- ∫exdx=ex+C\int e^xdx=e^x+C∫exdx=ex+C
- ∫sinxdx=−cosx+C\int sinxdx=-cosx+C∫sinxdx=−cosx+C
- ∫conxdx=sinx+C\int conxdx=sinx+C∫conxdx=sinx+C
- ∫sec2xdx=tanx+C\int sec^2xdx=tanx+C∫sec2xdx=tanx+C
- ∫scswxdx=−cotx+C\int scs^wxdx=-cotx+C∫scswxdx=−cotx+C
- ∫secxtanxdx=secx+C\int secxtanxdx=secx+C∫secxtanxdx=secx+C
- ∫cscxcotxdx=−cscx+C\int cscxcotxdx=-cscx+C∫cscxcotxdx=−cscx+C
- ∫11+x2dx=arctanx+C\int \frac{1}{1+x^2}dx=arctanx+C∫1+x21dx=arctanx+C
- ∫11−x2dx=arcsinx+C\int \frac{1}{\sqrt{1-x^2}}dx=arcsinx+C∫1−x21dx=arcsinx+C
- ∫1a2−x2dx=arcsinxa+C\int \frac{1}{\sqrt{a^2-x^2}}dx=arcsin\frac{x}{a}+C∫a2−x21dx=arcsinax+C
- ∫1a2+x2dx=1aarctanxa+C\int \frac{1}{a^2+x^2}dx=\frac{1}{a}arctan\frac{x}{a}+C∫a2+x21dx=a1arctanax+C
- ∫1x2−a2dx=12aln∣x−ax+a∣+C\int \frac{1}{x^2-a^2}dx=\frac{1}{2a}ln|\frac{x-a}{x+a}|+C∫x2−a21dx=2a1ln∣x+ax−a∣+C
- ∫1a2+x2dx=ln(x+x2+a2)+C\int \frac{1}{\sqrt{a^2+x^2}}dx=ln(x+\sqrt{x^2+a^2})+C∫a2+x21dx=ln(x+x2+a2)+C
- ∫1a2−x2dx=ln(x+x2−a2)+C\int \frac{1}{\sqrt{a^2-x^2}}dx=ln(x+\sqrt{x^2-a^2})+C∫a2−x21dx=ln(x+x2−a2)+C
- ∫secxdx=ln∣secx+tanx∣+C\int secxdx=ln|secx+tanx|+C∫secxdx=ln∣secx+tanx∣+C
- ∫cscxdx=−ln∣cscx+cotx∣+C\int cscxdx=-ln|cscx+cotx|+C∫cscxdx=−ln∣cscx+cotx∣+C
三种主要积分法
-
第一类换元积分法:设∫f(u)du=F(u)+C,u=φ(x)\int f(u)du=F(u)+C,u=\varphi(x)∫f(u)du=F(u)+C,u=φ(x)存在连续导数,则∫f[φ(x)]dφ(x)=F(φ(x))+C\int f[\varphi(x)]d\varphi(x)=F(\varphi(x))+C∫f[φ(x)]dφ(x)=F(φ(x))+C。常见的凑微分形式如下:
- ∫f(ax+b)dx=1a∫f(ax+b)d(ax+b)\int f(ax+b)dx=\frac{1}{a}\int f(ax+b)d(ax+b)∫f(ax+b)dx=a1∫f(ax+b)d(ax+b)
- ∫xmf(axm+b)dx=1(m+1)a∫f(axm+1+b)d(axm+1+b)(m≠1)\int x^mf(ax^m+b)dx=\frac{1}{(m+1)a}\int f(ax^{m+1}+b)d(ax^{m+1}+b)(m≠1)∫xmf(axm+b)dx=(m+1)a1∫f(axm+1+b)d(axm+1+b)(m=1)
- ∫f(x)dxx=2∫f(x)dx\int f(\sqrt x)\frac{dx}{\sqrt x}=2\int f(\sqrt x)d\sqrt x∫f(x)xdx=2∫f(x)dx
- ∫f(ex)exdx=∫f(ex)d(ex)\int f(e^x)e^xdx=\int f(e^x)d(e^x)∫f(ex)exdx=∫f(ex)d(ex)
- ∫f(lnx)1xdx=∫f(lnx)d(lnx)\int f(lnx)\frac{1}{x}dx=\int f(lnx)d(lnx)∫f(lnx)x1dx=∫f(lnx)d(lnx)
- ∫f(sinx)cosxdx=∫f(sinx)d(sinx)\int f(sinx)cosxdx=\int f(sinx)d(sinx)∫f(sinx)cosxdx=∫f(sinx)d(sinx)
- ∫f(cosx)sinxdx=−∫f(cosx)d(cosx)\int f(cosx)sinxdx=-\int f(cosx)d(cosx)∫f(cosx)sinxdx=−∫f(cosx)d(cosx)
- ∫f(tanx)1cos2xdx=∫f(tanx)d(tanx)\int f(tanx)\frac{1}{cos^2x}dx=\int f(tanx)d(tanx)∫f(tanx)cos2x1dx=∫f(tanx)d(tanx)
- ∫f(arcsinx)11−x2dx=∫f(arcsinx)d(arcsinx)\int f(arcsinx)\frac{1}{\sqrt{1-x^2}}dx=\int f(arcsinx)d(arcsinx)∫f(arcsinx)1−x21dx=∫f(arcsinx)d(arcsinx)
- ∫f(arctanx)11+x2dx=∫f(arctanx)d(arctanx)\int f(arctanx)\frac{1}{1+x^2}dx=\int f(arctanx)d(arctanx)∫f(arctanx)1+x21dx=∫f(arctanx)d(arctanx)
-
第二类换元积分法:设x=φ(x)x=\varphi(x)x=φ(x)是单调的、可导的函数,并且φ′(t)≠0\varphi'(t)≠0φ′(t)=0,又∫f[φ(x)]φ′(t)dt=F(t)+C\int f[\varphi(x)]\varphi'(t)dt=F(t)+C∫f[φ(x)]φ′(t)dt=F(t)+C,则∫f(x)dx=∫f[φ(t)]φ′(t)dt=F(t)+C=F[φ−1(x)]+C\int f(x)dx=\int f[\varphi(t)]\varphi'(t)dt=F(t)+C=F[\varphi^{-1}(x)]+C∫f(x)dx=∫f[φ(t)]φ′(t)dt=F(t)+C=F[φ−1(x)]+C,其中φ−1(x)\varphi^{-1}(x)φ−1(x)是x=φ(t)x=\varphi(t)x=φ(t)的反函数。常见的三种变量代换如下:
- 被积函数含有a2−x2\sqrt{a^2-x^2}a2−x2,令x=asint(或acost)x=asint(或acost)x=asint(或acost)
- 被积函数含有a2+x2\sqrt{a^2+x^2}a2+x2,令x=atantx=atantx=atant
- 被积函数含有x2−a2\sqrt{x^2-a^2}x2−a2,令x=asectx=asectx=asect
-
分步积分法:∫udv=uv−∫vdu\int udv=uv-\int vdu∫udv=uv−∫vdu。
- 何时用:出现两类函数相乘时使用。
- 如何用:
- ∫Pn(x)eaxdx\int P_n(x)e^{ax}dx∫Pn(x)eaxdx、∫Pn(x)sinaxdx\int P_n(x)sinaxdx∫Pn(x)sinaxdx、∫Pn(x)cosaxdx\int P_n(x)cosaxdx∫Pn(x)cosaxdx:将多项式以外凑进去。
- ∫Pn(x)lnxdx\int P_n(x)lnxdx∫Pn(x)lnxdx、∫Pn(x)arctanxdx\int P_n(x)arctanxdx∫Pn(x)arctanxdx、∫Pn(x)arcsinxdx\int P_n(x)arcsinxdx∫Pn(x)arcsinxdx:将多项式凑近去。
- ∫eaxsinβxdx\int e^{ax}sin\beta xdx∫eaxsinβxdx、∫eaxcosβxdx\int e^{ax}cos\beta xdx∫eaxcosβxdx:凑谁都可以。
三类常见可积函数积分
- 有理函数的积分(R(x)R(x)R(x)由xxx加减乘除得到):∫R(x)dx\int R(x)dx∫R(x)dx:
- 一般法(部分分式法)
- 特殊方法(加项减项拆或凑微分降幂)
- 三角有理式积分(R(sinx,cosx)R(sinx,cosx)R(sinx,cosx)由sinxsinxsinx和cosxcosxcosx加减乘除得到):∫R(sinx,cosx)dx\int R(sinx,cosx)dx∫R(sinx,cosx)dx:
- 一般方法(万能代换):令tanx2=ttan\frac{x}{2}=ttan2x=t,∫R(sinx,cosx)dx=∫R(2t1+t2,1−t21+t2)21+t2dt\int R(sinx,cosx)dx=\int R(\frac{2t}{1+t^2},\frac{1-t^2}{1+t^2})\frac{2}{1+t^2}dt∫R(sinx,cosx)dx=∫R(1+t22t,1+t21−t2)1+t22dt
- 特殊方法(三角变形、换元、分部)
- 若R(−sinx,cosx)=−R(sinx,cosx)R(-sinx,cosx)=-R(sinx,cosx)R(−sinx,cosx)=−R(sinx,cosx),则令u=cosxu=cosxu=cosx
- 若R(sinx,−cosx)=−R(sinx,cosx)R(sinx,-cosx)=-R(sinx,cosx)R(sinx,−cosx)=−R(sinx,cosx),则令u=sinxu=sinxu=sinx
- 若R(−sinx,−cosx)=R(sinx,cosx)R(-sinx,-cosx)=R(sinx,cosx)R(−sinx,−cosx)=R(sinx,cosx),则令u=tanxu=tanxu=tanx
- 简单无理函数的积分(开多少次方都可以,但里边必须是一次式比):∫R(x,ax+bcx+d)dx\int R(x,\sqrt\frac{ax+b}{cx+d})dx∫R(x,cx+dax+b)dx :
- 一般方法:令ax+bcx+d=t\sqrt\frac{ax+b}{cx+d}=tcx+dax+b=t。
定积分
概念
设函数f(x)f(x)f(x)在区间[a,b][a,b][a,b]上有定义且有界:
- 分割:在区间[a,b][a,b][a,b]中任意插入n−1n-1n−1个分点a=x0<x1<x2<...xn−1<xn=ba=x_0<x_1<x_2<...x_{n-1}<x_n=ba=x0<x1<x2<...xn−1<xn=b,将区间[a,b][a,b][a,b]分成nnn个小区间[xi−1,xi],i=1,2,...,n[x_{i-1},x_i],i=1,2,...,n[xi−1,xi],i=1,2,...,n,记Δxi=xi−xi−1\Delta x_i=x_i-x_{i-1}Δxi=xi−xi−1表示第iii个小区间的长度。
- 求和:在[xi−1,xi][x_{i-1},x_i][xi−1,xi]取一点ξ\xiξ,作和式∑i=1nf(ξi)Δxi\sum^n_{i=1}f(\xi_i)\Delta x_i∑i=1nf(ξi)Δxi,记λ=max[Δx1,Δx2,...Δxn]\lambda=max[\Delta x_1,\Delta x_2,...\Delta x_n]λ=max[Δx1,Δx2,...Δxn]。
- 取极限:若极限limλ→0∑i=1nf(ξi)Δxi\lim\limits_{\lambda \to 0}\sum_{i=1}^nf(\xi_i)\Delta x_iλ→0lim∑i=1nf(ξi)Δxi存在,且此极限不依赖于区间[a,b][a,b][a,b]的分法,也不依赖于点ξi\xi_iξi的取法,则称f(x)f(x)f(x)在区间[a,b][a,b][a,b]上可积,并称此极限为f(x)f(x)f(x)在区间[a,b][a,b][a,b]上的定积分,记为∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx,即∫abf(x)dx=limλ→0∑i=1nf(ξi)Δxi\int_a^bf(x)dx=\lim\limits_{\lambda\to 0}\sum_{i=1}^nf(\xi_i)\Delta x_i∫abf(x)dx=λ→0lim∑i=1nf(ξi)Δxi。
定积分存在的充分条件:
- 若f(x)f(x)f(x)在[a,b][a,b][a,b]上连续,则∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx必定存在。
- 若f(x)f(x)f(x)在[a,b][a,b][a,b]上有界,且只有有限个间断点,则∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx必定存在。
- 若f(x)f(x)f(x)在[a,b][a,b][a,b]上只有有限个第一类间断点,则∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx必定存在。
几何意义
- 设∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx存在,若在[a,b][a,b][a,b]上f(x)≥0f(x)≥0f(x)≥0,则∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx的值等于以曲线t=f(x),x=a,x=bt=f(x),x=a,x=bt=f(x),x=a,x=b及xxx轴所围成的曲边梯形的面积。
- 若在[a,b][a,b][a,b]上f(x)≤0f(x)≤0f(x)≤0,则∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx的值等于以曲线y=f(x),x=a,x=by=f(x),x=a,x=by=f(x),x=a,x=b及xxx轴所围成的曲边梯形面积的负值。
- 若在[a,b][a,b][a,b]上f(x)f(x)f(x)的值有正也有负,则∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx的值等于xxx轴上方的面积减去xxx轴下方的面积所得之差。
性质
不等式性质:
- 若在区间[a,b][a,b][a,b]上f(x)≤g(x)f(x)≤g(x)f(x)≤g(x)且a<=ba<=ba<=b,则∫abf(x)dx≤∫abg(x)dx\int_a^bf(x)dx≤\int_a^bg(x)dx∫abf(x)dx≤∫abg(x)dx。
- 若MMM及mmm分别是f(x)f(x)f(x)在[a,b][a,b][a,b]上的最大值和最小值,则m(b−a)≤∫abf(x)dx≤M(b−a)m(b-a)≤\int_a^bf(x)dx≤M(b-a)m(b−a)≤∫abf(x)dx≤M(b−a)。
- ∣∫abf(x)dx∣≤∫ab∣f(x)∣dx|\int_a^bf(x)dx|≤\int_a^b|f(x)|dx∣∫abf(x)dx∣≤∫ab∣f(x)∣dx。
中值定理:
- 若f(x)f(x)f(x)在[a,b][a,b][a,b]上连续,则∫abf(x)dx=f(ξ)(b−a)(a<ξ<b)\int_a^bf(x)dx=f(\xi)(b-a)(a<\xi<b)∫abf(x)dx=f(ξ)(b−a)(a<ξ<b)。常称1b−a∫abf(x)dx\frac{1}{b-a}\int_a^bf(x)dxb−a1∫abf(x)dx为函数f(x)f(x)f(x)在区间[a,b][a,b][a,b]上的平均值。
- 若f(x),g(x)f(x),g(x)f(x),g(x)在[a,b][a,b][a,b]上连续,g(x)g(x)g(x)不变号,则∫abf(x)g(x)dx=f(ξ)∫abg(x)dx(a≤ξ≤b)\int_a^bf(x)g(x)dx=f(\xi)\int_a^bg(x)dx(a≤\xi≤b)∫abf(x)g(x)dx=f(ξ)∫abg(x)dx(a≤ξ≤b)。
积分上限的函数
变上限的积分∫axf(t)dt\int_a^xf(t)dt∫axf(t)dt是其上限xxx的函数,常称之为积分上限函数。
- 如果f(x)f(x)f(x)在区间[a,b][a,b][a,b]上连续,则Φ(x)=∫axf(t)dt\Phi(x)=\int_a^xf(t)dtΦ(x)=∫axf(t)dt在[a,b][a,b][a,b]上可导,且(Φ(x))′=f(x)(\Phi(x))'=f(x)(Φ(x))′=f(x)。
- 如果f(x)f(x)f(x)在区间[a,b][a,b][a,b]上连续,且φ1(x),φ2(x)\varphi_1(x),\varphi_2(x)φ1(x),φ2(x)为可导函数,则(∫φ1(x)φ2(x))′=f[φ2(x)]×φ2′(x)−f[φ1(x)]×φ1′(x)(\int_{\varphi_1(x)}^{\varphi_2(x)})'=f[\varphi_2(x)]\times\varphi_2'(x)-f[\varphi_1(x)]\times\varphi_1'(x)(∫φ1(x)φ2(x))′=f[φ2(x)]×φ2′(x)−f[φ1(x)]×φ1′(x)。
- 如果f(x)f(x)f(x)在[−l,l][-l,l][−l,l]上连续,则如果f(x)f(x)f(x)为奇函数,那么∫0xf(t)dt\int_0^xf(t)dt∫0xf(t)dt为奇函数;如果f(x)f(x)f(x)为偶函数,那么∫0xf(t)dt\int_0^xf(t)dt∫0xf(t)dt为偶函数。
定积分的计算
-
莱布尼茨公式:设f(x)f(x)f(x)在区间[a,b][a,b][a,b]上连续,F(x)F(x)F(x)为f(x)f(x)f(x)在[a,b][a,b][a,b]上的一个原函数,则有∫abf(x)dx=F(x)∣ab=F(b)−F(a)\int_a^bf(x)dx=F(x)|_a^b=F(b)-F(a)∫abf(x)dx=F(x)∣ab=F(b)−F(a)。
-
换元积分法:设f(x)f(x)f(x)在区间III上连续,函数x=φ(t)x=\varphi(t)x=φ(t)满足下列条件:φ(α)=a,φ(β)=b\varphi(\alpha)=a,\varphi(\beta)=bφ(α)=a,φ(β)=b; φ(t)\varphi(t)φ(t)在[α,β](或[β,α])[\alpha,\beta](或[\beta,\alpha])[α,β](或[β,α])上有连续导数,且RφIR_\varphi IRφI,则∫abf(x)dx=∫αβf(φ(t))φ′(t)dt\int_a^bf(x)dx=\int_{\alpha}^{\beta}f(\varphi (t)) \varphi '(t)dt∫abf(x)dx=∫αβf(φ(t))φ′(t)dt。
-
分步积分法:∫baudv=uv∣ba−∫bavdu\int_b^audv=uv|_b^a-\int_b^avdu∫baudv=uv∣ba−∫bavdu。
-
利用奇偶性和周期性
- 设函数f(x)f(x)f(x)为[−a,a][-a,a][−a,a]上的连续函数(a>0),则∫−aaf(x)dx={0,f(x)为奇函数时2∫0af(x)dx,f(x)为偶函数时\int_{-a}^af(x)dx= \begin{cases} 0,f(x)为奇函数时\\ 2\int_0^af(x)dx,f(x)为偶函数时\\ \end{cases}∫−aaf(x)dx={0,f(x)为奇函数时2∫0af(x)dx,f(x)为偶函数时
- 设f(x)f(x)f(x)是以TTT为周期的连续函数,则对任意给数aaa,总有∫aa+Tf(x)dx=∫0Tf(x)dx\int_a^{a+T}f(x)dx=\int_0^Tf(x)dx∫aa+Tf(x)dx=∫0Tf(x)dx。
-
利用已知公式:
- ∫0π2sinnxdx=∫0π2cosnxdx={n−1n×n−3n−2×...×12×π2,n为正偶数n−1n×n−3n−2×...×23,n为大于1的奇数\int_0^{\frac{\pi}{2}}sin^nxdx=\int_0^{\frac{\pi}{2}}cos^nxdx=\begin{cases} \frac{n-1}{n}\times\frac{n-3}{n-2}\times...\times\frac{1}{2}\times\frac{\pi}{2},n为正偶数\\\frac{n-1}{n}\times\frac{n-3}{n-2}\times...\times\frac{2}{3},n为大于1的奇数\end{cases}∫02πsinnxdx=∫02πcosnxdx={nn−1×n−2n−3×...×21×2π,n为正偶数nn−1×n−2n−3×...×32,n为大于1的奇数
- ∫0πxf(sinx)dx=π2∫0πf(sinx)dx,其中f(x)连续\int_0^\pi xf(sinx)dx=\frac{\pi}{2}\int_0^\pi f(sinx)dx,其中f(x)连续∫0πxf(sinx)dx=2π∫0πf(sinx)dx,其中f(x)连续
几何应用
平面曲线的面积:
- 若平面域DDD由曲线y=f(x),y=g(x)(f(x)≥g(x)),x=a,x=b(a<b)y=f(x),y=g(x)(f(x)≥g(x)),x=a,x=b(a<b)y=f(x),y=g(x)(f(x)≥g(x)),x=a,x=b(a<b)所围成,则平面区域DDD的面积为S=∫ab[f(x)−g(x)]dxS=\int_a^b[f(x)-g(x)]dxS=∫ab[f(x)−g(x)]dx。
- 若平面域DDD由曲线r=r(θ),θ=α,θ=β(α<β)r=r(\theta),\theta=\alpha,\theta=\beta(\alpha<\beta)r=r(θ),θ=α,θ=β(α<β)所围成,则其面积为S=12∫αβr2(θ)dθS=\frac{1}{2}\int_{\alpha}^{\beta}r^2(\theta)d\thetaS=21∫αβr2(θ)dθ。
旋转体体积:若区域DDD由曲线y=f(x)(f(x)≥0)y=f(x)(f(x)≥0)y=f(x)(f(x)≥0)和直线x=a,x=b(0≤a<b)x=a,x=b(0≤a<b)x=a,x=b(0≤a<b)及xxx轴所围成,则:
- 区域DDD绕xxx轴旋转一周所得到的旋转体的体积为Vx=π∫abf2(x)dxV_x=\pi\int_a^bf^2(x)dxVx=π∫abf2(x)dx。
- 区域DDD绕yyy轴旋转一周所得到的旋转体的体积为Vy=2π∫abxf(x)dxV_y=2\pi\int_a^bxf(x)dxVy=2π∫abxf(x)dx。
曲线弧长:
- C:y=y(x),a≤x≤b,s=∫ab1+y′2dxC:y=y(x),a≤x≤b,s=\int_a^b\sqrt{1+y'^2}dxC:y=y(x),a≤x≤b,s=∫ab1+y′2dx。
- C:{x=x(t),y=y(t),a≤t≤b,s=∫abx′2+y′2dtC:\begin{cases}x=x(t),\\y=y(t),\end{cases}a≤t≤b,s=\int_a^b\sqrt{x'^2+y'^2}dtC:{x=x(t),y=y(t),a≤t≤b,s=∫abx′2+y′2dt。
- C:r=r(θ),a≤θ≤b,s=∫abr2+r′2dθC:r=r(\theta),a≤\theta≤b,s=\int_a^b\sqrt{r^2+r'^2}d\thetaC:r=r(θ),a≤θ≤b,s=∫abr2+r′2dθ。
旋转体侧面积:曲线y=f(x)(f(x)≥0)y=f(x)(f(x)≥0)y=f(x)(f(x)≥0)和直线x=a,x=b(0≤a<b)x=a,x=b(0≤a<b)x=a,x=b(0≤a<b)及xxx轴所围成区域绕xxx轴旋转所得旋转体的侧面积为S=2π∫abf(x)1+f′2(x)dxS=2\pi\int_a^bf(x)\sqrt{1+f'^2(x)}dxS=2π∫abf(x)1+f′2(x)dx。
反常积分
无穷区间的反常积分
- 设f(x)f(x)f(x)为[a,+∞)[a,+\infty)[a,+∞)上的连续函数,如果极限limt→+∞∫atf(x)dx\lim\limits_{t\to+\infty}\int_a^tf(x)dxt→+∞lim∫atf(x)dx存在,则称此极限为函数f(x)f(x)f(x)在无穷区间[a,+∞)[a,+\infty)[a,+∞)上的反常积分,记作∫a+∞f(x)dx\int_a^{+\infty}f(x)dx∫a+∞f(x)dx,即∫a+∞f(x)dx=limt→+∞∫atf(x)dx\int_a^{+\infty}f(x)dx=\lim\limits_{t\to+\infty}\int_a^tf(x)dx∫a+∞f(x)dx=t→+∞lim∫atf(x)dx。这时也称反常积分∫a+∞f(x)dx\int_a^{+\infty}f(x)dx∫a+∞f(x)dx收敛,如果上述极限不存在,则称反常积分∫a+∞f(x)dx\int_a^{+\infty}f(x)dx∫a+∞f(x)dx发散。
- 设f(x)f(x)f(x)为(−∞,b](-\infty,b](−∞,b]上的连续函数,则可类似的定义函数f(x)f(x)f(x)在无穷区间(−∞,b](-\infty,b](−∞,b]上的反常积分∫−∞0f(x)dx=limt→−∞∫tbf(x)dx\int_{-\infty}^0f(x)dx=\lim\limits_{t\to -\infty}\int_t^bf(x)dx∫−∞0f(x)dx=t→−∞lim∫tbf(x)dx。
- 设f(x)f(x)f(x)为(−∞,+∞)(-\infty,+\infty)(−∞,+∞)上的连续函数,如果反常积分∫−∞0f(x)dx\int_{-\infty}^0f(x)dx∫−∞0f(x)dx和∫0+∞f(x)dx\int_{0}^{+\infty}f(x)dx∫0+∞f(x)dx都收敛,则称反常积分∫−∞+∞f(x)dx\int_{-\infty}^{+\infty}f(x)dx∫−∞+∞f(x)dx收敛,且∫−∞+∞f(x)dx=∫−∞0f(x)dx+∫0+∞f(x)dx\int_{-\infty}^{+\infty}f(x)dx=\int_{-\infty}^0f(x)dx+\int_{0}^{+\infty}f(x)dx∫−∞+∞f(x)dx=∫−∞0f(x)dx+∫0+∞f(x)dx;如果∫−∞0f(x)dx\int_{-\infty}^0f(x)dx∫−∞0f(x)dx和∫0+∞f(x)dx\int_{0}^{+\infty}f(x)dx∫0+∞f(x)dx至少有一个发散,则称∫−∞+∞f(x)dx\int_{-\infty}^{+\infty}f(x)dx∫−∞+∞f(x)dx发散。
比较判别法:设f(x),g(x)f(x),g(x)f(x),g(x)在[a,+∞)[a,+\infty)[a,+∞)上连续,且0≤f(x)≤g(x)0≤f(x)≤g(x)0≤f(x)≤g(x),则:
- 当∫a+∞g(x)dx\int_a^{+\infty}g(x)dx∫a+∞g(x)dx收敛时,∫a+∞f(x)dx\int_a^{+\infty}f(x)dx∫a+∞f(x)dx收敛。
- 当∫a+∞f(x)dx\int_a^{+\infty}f(x)dx∫a+∞f(x)dx收敛时,∫a+∞g(x)dx\int_a^{+\infty}g(x)dx∫a+∞g(x)dx收敛。
比较判别法的极限形式:设f(x),g(x)f(x),g(x)f(x),g(x)在(a,+∞](a,+\infty](a,+∞]上非负连续,且limx→+∞f(x)g(x)=λ\lim\limits_{x\to +\infty}\frac{f(x)}{g(x)}=\lambdax→+∞limg(x)f(x)=λ(有限或无穷),则:
- 当λ≠0\lambda≠0λ=0时,∫a+∞f(x)dx\int_a^{+\infty} f(x)dx∫a+∞f(x)dx与∫a+∞g(x)dx\int_a^{+\infty}g(x)dx∫a+∞g(x)dx同敛散。
- 当λ=0\lambda=0λ=0时,若∫a+∞g(x)dx\int_a^{+\infty}g(x)dx∫a+∞g(x)dx收敛,则∫a+∞f(x)dx\int_a^{+\infty}f(x)dx∫a+∞f(x)dx也收敛。
- 当λ=+∞\lambda=+\inftyλ=+∞时,若∫a+∞g(x)dx\int_a^{+\infty}g(x)dx∫a+∞g(x)dx发散,则∫a+∞f(x)dx\int_a^{+\infty}f(x)dx∫a+∞f(x)dx也发散。
常用结论:∫a+∞1xpdx{p>1,收敛p≤1,发散(a>0)\int_a^{+\infty}\frac{1}{x^p}dx\begin{cases}p>1,收敛\\p≤1,发散\end{cases}(a>0)∫a+∞xp1dx{p>1,收敛p≤1,发散(a>0)
无界函数的反常积分
如果函数f(x)f(x)f(x)在点aaa 的任何一邻域内都无界,那么点aaa称为f(x)f(x)f(x)的瑕点(也称为无界点),无界函数的反常积分也成为瑕积分。
- 设函数f(x)f(x)f(x)在(a,b](a,b](a,b]上连续,点aaa为f(x)f(x)f(x)的瑕点,如果极限limt→a+∫tbf(x)dx\lim\limits_{t\to a^+}\int_t^bf(x)dxt→a+lim∫tbf(x)dx存在,则称此极限为函数f(x)f(x)f(x)在区间[a,b][a,b][a,b]上的反常积分,记作∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx,即∫abf(x)dx=limt→a+∫tbf(x)dx\int_a^bf(x)dx=\lim\limits_{t\to a^+}\int_t^bf(x)dx∫abf(x)dx=t→a+lim∫tbf(x)dx。这时也称反常积分∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx收敛,如果上述极限不存在,则称反常积分∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx发散。
- 设函数f(x)f(x)f(x)在(a,b](a,b](a,b]上连续,点bbb为f(x)f(x)f(x)的瑕点,则可类似的定义函数f(x)f(x)f(x)在无穷区间[a,b][a,b][a,b]上的反常积分∫abf(x)dx=limt→b−∫atf(x)dx\int_{a}^bf(x)dx=\lim\limits_{t\to b^-}\int_a^tf(x)dx∫abf(x)dx=t→b−lim∫atf(x)dx。
- 设函数f(x)f(x)f(x)在[a,b][a,b][a,b]上除点c(a<c<b)c(a<c<b)c(a<c<b)外连续,点ccc为函数f(x)f(x)f(x)的瑕点,如果反常积分∫acf(x)dx\int_a^cf(x)dx∫acf(x)dx和∫cbf(x)dx\int_c^bf(x)dx∫cbf(x)dx都收敛,则称反常积分∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx收敛,且∫abf(x)dx=∫acf(x)dx+∫cbf(x)dx\int_a^bf(x)dx=\int_a^cf(x)dx+\int_c^bf(x)dx∫abf(x)dx=∫acf(x)dx+∫cbf(x)dx。如果反常积分∫acf(x)dx\int_a^cf(x)dx∫acf(x)dx和∫cbf(x)dx\int_c^bf(x)dx∫cbf(x)dx至少有一个发散,则称反常积分∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx发散。
比较判别法:设f(x),g(x)f(x),g(x)f(x),g(x)在[a,+∞)[a,+\infty)[a,+∞)上连续,且0≤f(x)≤g(x),x=a0≤f(x)≤g(x),x=a0≤f(x)≤g(x),x=a为f(x)f(x)f(x)和g(x)g(x)g(x)的瑕点,则:
- 当∫abg(x)dx\int_a^bg(x)dx∫abg(x)dx收敛时,∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx收敛。
- 当∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx收敛时,∫abg(x)dx\int_a^bg(x)dx∫abg(x)dx收敛。
比较判别法的极限形式:设f(x),g(x)f(x),g(x)f(x),g(x)在(a,b](a,b](a,b]上非负连续,且limx→a+f(x)g(x)=λ\lim\limits_{x\to a^+}\frac{f(x)}{g(x)}=\lambdax→a+limg(x)f(x)=λ(有限或无穷),则:
- 当λ≠0\lambda≠0λ=0时,∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx与∫abg(x)dx\int_a^bg(x)dx∫abg(x)dx同敛散。
- 当λ=0\lambda=0λ=0时,若∫abg(x)dx\int_a^bg(x)dx∫abg(x)dx收敛,则∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx也收敛。
- 当λ=+∞\lambda=+\inftyλ=+∞时,若∫abg(x)dx\int_a^bg(x)dx∫abg(x)dx发散,则∫abf(x)dx\int_a^bf(x)dx∫abf(x)dx也发散。
常用结论:
- ∫ab1(x−a)dx{p<1,收敛p≥1,发散\int_a^b\frac{1}{(x-a)}dx\begin{cases}p<1,收敛\\p≥1,发散\end{cases}∫ab(x−a)1dx{p<1,收敛p≥1,发散
- ∫ab1(b−x)dx{p<1,收敛p≥1,发散\int_a^b\frac{1}{(b-x)}dx\begin{cases}p<1,收敛\\p≥1,发散\end{cases}∫ab(b−x)1dx{p<1,收敛p≥1,发散
相关文章:

高等数学——定积分和不定积分
文章目录不定积分概念几何意义性质不定积分的基本公式三种主要积分法三类常见可积函数积分定积分概念几何意义性质积分上限的函数定积分的计算几何应用反常积分无穷区间的反常积分无界函数的反常积分不定积分 不定积分是导数的逆运算。 概念 原函数:设f(x)f(x)f(…...
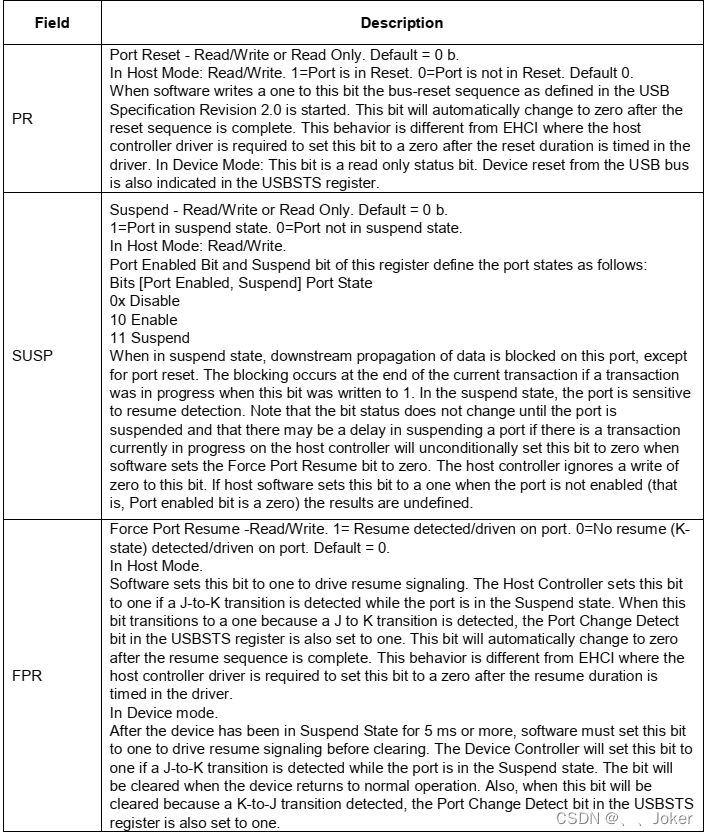
imx6 usb增强信号强度
USB信号 参考:官方文档 USB信号完整性取决于许多因素,如电路设计、PCB布局、堆叠和阻抗。每个产品可能彼此不同,因此客户需要微调参数,以获得最佳的信号质量。 测试板已经路由出两个USB端口:一个OTG1,一个主机。每个端…...

深入理解性能压测工具原理
如果没有性能测试工具如何通过手工实现 如果没有性能测试工具,通过手工进行性能测试,这是一个值得我们思考的问题。这时候需要一个协调员发送指令,一个操作员进行操作,对系统施加压力,多个操作员代表着多个用户进行并…...
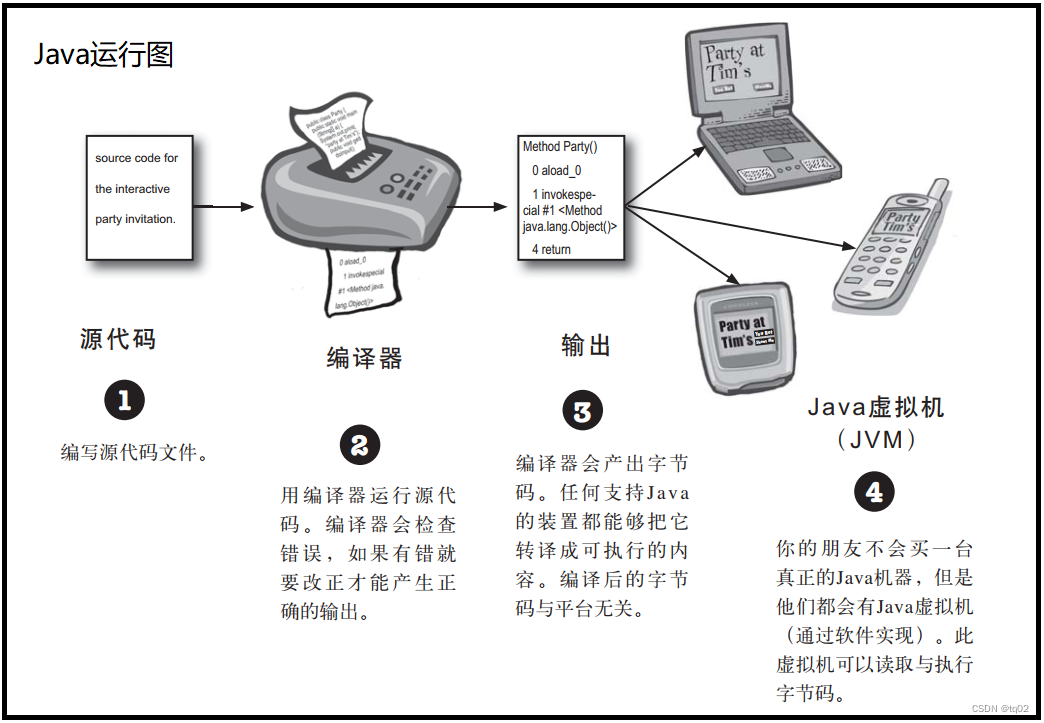
Java的概述和运行方式
目录 一.Java是什么? 1.1Java的目前状况和学习需求 1.2Java的平台分类和特点 二.Java程序的运行方式 2.1 Java的程序结构 2.2 JDK、JRE、JVM的关系 2.3 Java运行详情 总结 😽个人主页:tq02的博客_CSDN博客-领域博主 🌈理想…...

【C语言】每日刷题 —— 牛客
前言 大家好,今天带来一篇新的专栏 c_牛客,不出意外的话每天更新十道题,难度也是从易到难,自己复习的同时也希望能帮助到大家,题目答案会根据我所学到的知识提供最优解。 🏡个人主页:悲伤的猪大…...
JavaEE课程实践-Servlet的部署(tomcat服务器)
目录 Servlet简述 tomcat服务器的安装和运行 Servlet的部署 部署具体步骤 一、创建maven工程 二、创建Servlet类 三、导入相应jar包 四、编写Servlet代码 五、运行maven项目,启动tomcat服务器 六、测试访问是否成功。 Servlet简述 Servlet 是 Java EE 技术…...
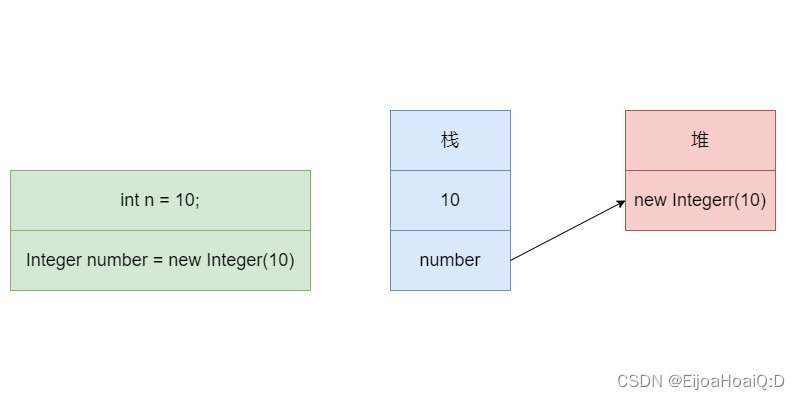
Java 中的拆箱和装箱
在 Java 中,每个基本数据类型都对应了一个包装类型,比如:int 的包装类型是 Integer,double 的包装类型是 Double…那么,基本数据类型和包装类型有什么区别呢? 大概有以下几点区别: 成员变量的…...

从0开始自制解释器——实现多位整数的加减法计算器
上一篇我们实现了一个简单的加法计算器,并且了解了基本的词法分析、词法分析器的概念。本篇我们将要对之前实现的加法计算器进行扩展,我们为它添加以下几个功能 计算减法能自动识别并跳过空白字符不再局限于单个整数,而是能计算多位整数 提…...
C#传智:File类,泛型,字典,FileStream,StreamReader,多态)
(12)C#传智:File类,泛型,字典,FileStream,StreamReader,多态
内容有点多,重点:泛型、字典,流与多态。 继续深入学习内容:List、Dictionary、using语句、FileStream 一、File类的继续学心 File.ReadAllLines(string path,Encoding,encoding)指定编码读取返回行字串数组 File.WriteAllText(string…...

Dubbo的服务暴漏与服务发现源码详解
服务暴漏 如果配置需要刷新则根据配置优先级刷新服务配置 如果服务已经导出,则直接返回 是否异步导出(全局或者服务级别配置了异步,则需要异步导出服务) 服务暴漏入口DefaultModuleDeployer#exportServices private void exp…...
Python 的IDE——PyCharm
IDE介绍与安装 介绍 集成开发环境(IDE) 集成开发环境(IDE,integrated Development Environment) —— 集成开发软件需要的所有工具,一般包括以下工具: 图形用户界面 代码编辑器(支持代码补全、自动缩进) 编译器/解释器 调试器…...
模块)
01 C语言使用链表实现队列(Queue、FIFO)模块
01 C语言使用链表实现队列(Queue、FIFO)模块 作者将狼才鲸创建日期2023-03-08Gitee源码仓库地址:C语言使用链表实现队列(Queue、FIFO)模块 Linux原生的队列KFIFO一次只能操作一个队列,操作变长元素时&…...
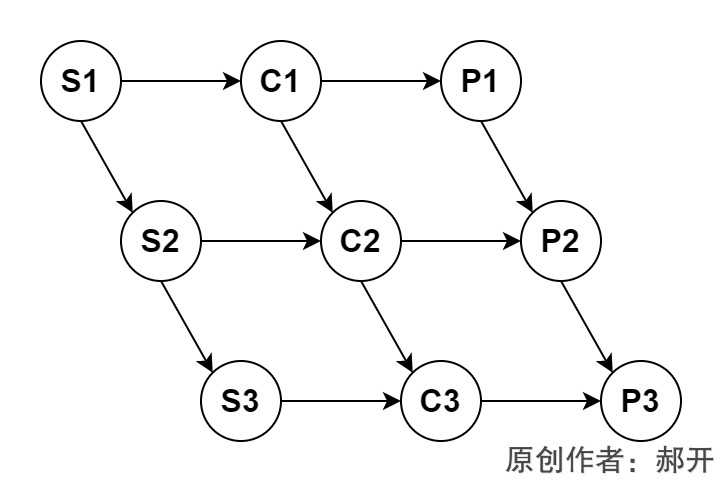
2.2操作系统-进程管理:前趋图、前趋图与PV操作
2.1操作系统-进程管理:前趋图\前趋图与PV操作前趋图前趋图与PV操作练习前趋图与PV操作,一般出现了,分值在2~3分左右,技巧性很强。 前趋图 前趋图是为了描述一个程序的各部分间的依赖关系,或者是一个大的计算的各个子…...

凤凰游攻略
凤凰游攻略1 装备📦1.1 证件1.2 日常用品1.3 药品1.4 衣物1.5 洗漱用品2 交通🚗3 住宿🏠4 美食🍕5 拍照📷5.1 租苗族服5.1.1 单租服装5.1.2 服装化妆5.2 一条龙旅拍6 路线🗺️景点🏙️7 注意⚠️…...
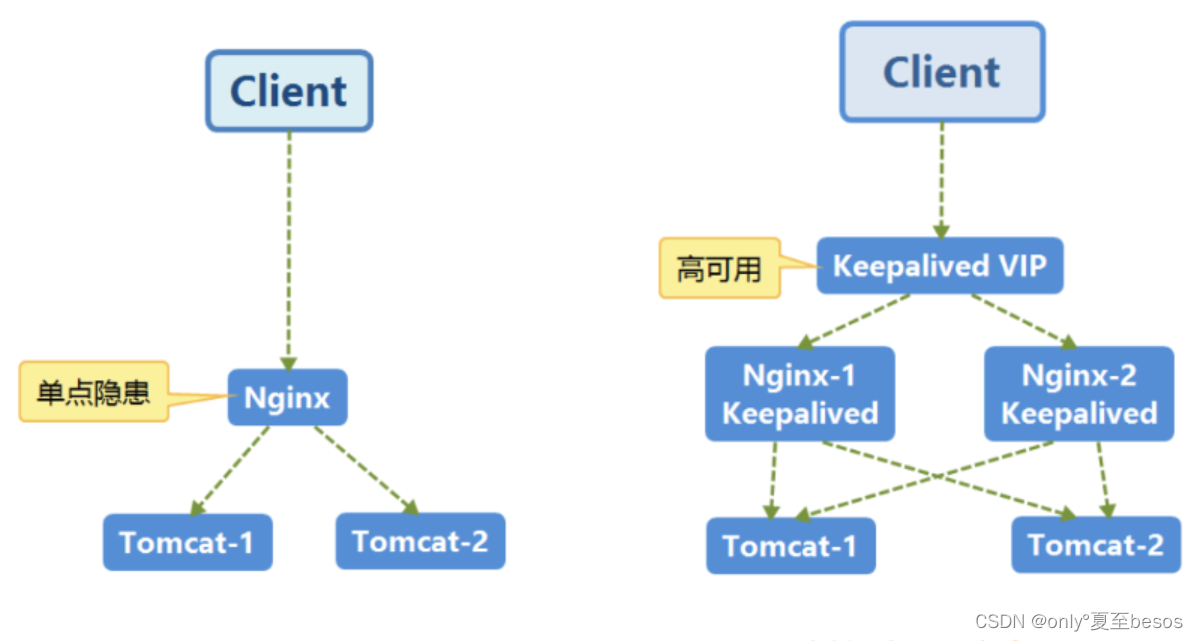
Nginx 高可用方案
准备工作 10.10.4.5 10.10.4.6 VIP:10.10.4.10 两台虚拟机。安装好Nginx 安装Nginx 更新yum源文件: rpm -ivh http://nginx.org/packages/centos/7/noarch/RPMS/nginx-release-centos-7-0.el7.ngx.noarch.rpm wget -O /etc/yum.repos.d/CentOS-Ba…...
Linux基本指令
文章目录 常用Linux命令常见Linux指令 1、ls指令 语法:ls [选项][目录或文件] 功能:对于目录,该命令列出该目录下的所有子目录与文件。对于文件,将列出文件名以及其他信息。常用选项: -a 列出目录下的所有文件…...

Linux系统基础命令(二)
一、浏览和切换目录 ls命令:列出文件和目录,主要用于列出文件和目录 CentOS的终端默认是有颜色标注的。一般来说:蓝色--->目录;绿色-->可执行文件;红色--->压缩文件;浅蓝色--->链接文件&#…...

【C++】C++11——简介|列表初始|简化声明|nullptr与范围for|STL中的变化
文章目录一、C11简介二、列表初始化三、简化声明四、nullptr与范围for五、STL中一些变化一、C11简介 在2003年C标准委员会曾经提交了一份技术勘误表(简称TC1),使得C03这个名字已经取代了C98称为C11之前的最新C标准名称。不过由于TC1主要是对C98标准中的漏洞进行修复…...
Python -- 函数
文章目录1、一个简单的函数2、多参数函数3、返回值3.1、简单的返回3.2、返回列表和字典4、传入列表5、传入任意数量的实参5.1、以元组和字典的形式5.2、形参的排列顺序6、将函数储存在模块中1、一个简单的函数 函数用关键字def来定义,传参时不用指定参数类型 para&…...

Pytorch中utils.data 与torchvision简介
Pytorch中utils.data 与torchvision简介1 数据处理工具概述2 utils.data简介3 torchvision简介3.1 transforms3.2 ImageFolder1 数据处理工具概述 Pytorch涉及数据处理(数据装载、数据预处理、数据增强等)主要工具包及相互关系如下图所示,主…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
