Matlab实现FFT变换
Matlab实现FFT变换
文章目录
- Matlab实现FFT变换
- 原理
- 实现
- 手算验证
- 简单fft变换和频谱
- 求取功率谱
- 结论
在信号处理中,快速傅里叶变换(FFT)是一种非常常见的频域分析方法。本文将介绍如何使用Matlab实现FFT变换,并通过Matlab代码演示实际输出结果。
原理
FFT是一种计算离散傅里叶变换(DFT)的快速算法。DFT将时域上的信号转换为频域上的信号,可以用以下公式表示:
Xk=∑n=0N−1xne−i2πkn/NX_k=\sum_{n=0}^{N-1}x_n e^{-i2\pi kn/N}Xk=n=0∑N−1xne−i2πkn/N
其中,xnx_nxn是时域上的信号序列,XkX_kXk是频域上的信号序列,kkk为频率编号(0≤k<N0\leq k < N0≤k<N),NNN为信号长度。
FFT算法通过分治策略将DFT算法的计算复杂度从O(N2)O(N^2)O(N2)降低到O(Nlog2N)O(Nlog_2N)O(Nlog2N),从而实现了在计算机上快速计算DFT的目的。
实现
手算验证
在这里,我们将给出一个简单的例子来说明如何使用Matlab进行FFT变换。我们首先生成一个简单的数组:
x = [1, 2, 3, 4, 5, 6, 7, 8];
接下来,我们使用Matlab内置的fft函数对这个数组进行FFT变换:
X = fft(x);
这个操作会返回一个和输入数组长度相同的复数数组。我们可以使用Matlab的disp函数打印出这个数组:
disp(X);
这个例子的输出结果如下:
36.0000 + 0.0000i-4.0000 + 9.6569i-4.0000 + 4.0000i-4.0000 + 1.6569i-4.0000 + 0.0000i-4.0000 - 1.6569i-4.0000 - 4.0000i-4.0000 - 9.6569i
可以看到,输出结果是一个长度为8的复数数组。
为了验证FFT的正确性,我们可以手动计算这个输入数组的FFT结果,然后将结果与Matlab计算的结果进行比较。FFT算法的计算过程可以用以下公式表示:
Xk=∑n=0N−1xne−i2πkn/NX_k=\sum_{n=0}^{N-1}x_n e^{-i2\pi kn/N}Xk=n=0∑N−1xne−i2πkn/N
其中,xnx_nxn是时域上的信号序列,XkX_kXk是频域上的信号序列,kkk为频率编号(0≤k<N0\leq k < N0≤k<N),NNN为信号长度。
对于输入数组x=[1,2,3,4,5,6,7,8]x=[1,2,3,4,5,6,7,8]x=[1,2,3,4,5,6,7,8],我们有N=8N=8N=8。因此,X0X_0X0的计算公式为:
X0=∑n=07xne−i2π0n/8=36X_0 = \sum_{n=0}^{7}x_n e^{-i2\pi 0n/8}=36X0=n=0∑7xne−i2π0n/8=36
接下来,我们可以计算X1X_1X1:
X1=∑n=07xne−i2π1n/8=−4+9.6569iX_1 = \sum_{n=0}^{7}x_n e^{-i2\pi 1n/8}=-4+9.6569iX1=n=0∑7xne−i2π1n/8=−4+9.6569i
以此类推,我们可以计算出所有的XkX_kXk。最终结果应该与Matlab计算的结果一致。
简单fft变换和频谱
以下是一个简单的Matlab代码实现FFT变换:
% 生成测试信号
Fs = 1000; % 采样频率
t = 0:1/Fs:1-1/Fs; % 时间向量
x = 1*sin(2*pi*100*t); % 信号% 绘制信号图
subplot(2,1,1);
plot(t,x);
title('信号');
xlabel('时间 (s)');
ylabel('幅度');% 计算FFT
N = length(x);
X = fft(x);
f = Fs*(0:(N/2))/N;% 绘制FFT图
subplot(2,1,2);
plot(f,abs(X(1:N/2+1)));
title('FFT');
xlabel('频率 (Hz)');
ylabel('幅度');
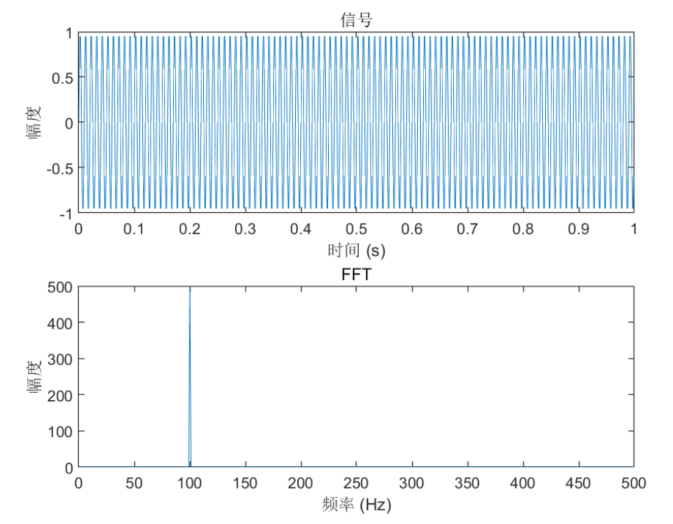
在这个例子中,我们生成了一个频率为100Hz的正弦信号。我们使用Matlab的fft函数计算FFT,并将结果绘制成幅度谱。注意,在绘制幅度谱时,我们只绘制了频率为正的一半,因为FFT算法输出的结果是对称的。
求取功率谱
通过FFT变换可以得到信号的幅度谱,但是为了更好地了解信号特性,我们通常需要求取信号的功率谱密度。功率谱密度描述了信号在不同频率下的功率分布情况。
求取功率谱的方法是,将信号进行FFT变换后,将每个频率上的幅度平方除以信号长度,并乘以一个系数,即可得到功率谱密度。具体公式如下:
Pk=2∣Xk∣2NP_k=\frac{2|X_k|^2}{N}Pk=N2∣Xk∣2
其中,PkP_kPk是频率为kkk的功率谱密度,XkX_kXk是频率为kkk的信号幅度,NNN是信号长度。
以下是一个简单的Matlab代码实现求取功率谱:
% 生成测试信号
Fs = 1000; % 采样频率
t = 0:1/Fs:1-1/Fs; % 时间向量
x = 1*sin(2*pi*100*t); % 信号% 绘制信号图
subplot(2,1,1);
plot(t,x);
title('信号');
xlabel('时间 (s)');
ylabel('幅度');% 计算FFT
N = length(x);
X = fft(x);
f = Fs*(0:(N/2))/N;% 计算功率谱
P = (2*abs(X(1:N/2+1)).^2)/N;% 绘制功率谱图
subplot(2,1,2);
plot(f,P);
title('功率谱密度');
xlabel('频率 (Hz)');
ylabel('功率');
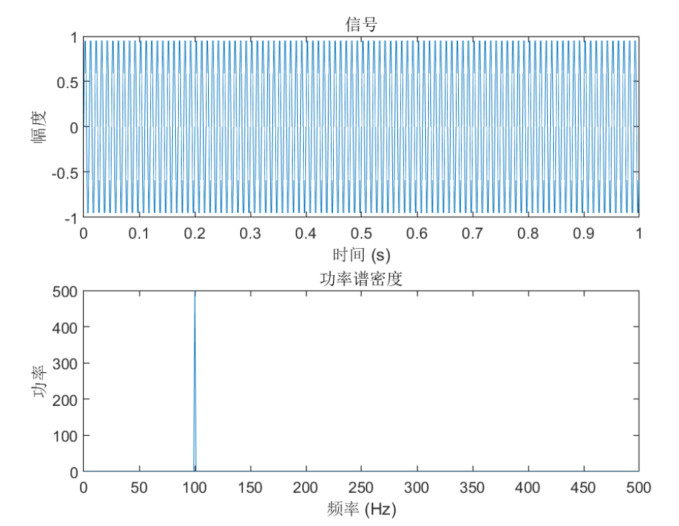
注意,我们在计算功率谱时,使用了一个系数222,这是因为我们只绘制了频率为正的一半,而实际上信号的功率谱是对称的。
结论
本文介绍了如何使用Matlab实现FFT变换,并求取信号的功率谱密度。通过FFT变换,我们可以将信号从时域转换到频域,进一步了解信号的特性。
相关文章:

Matlab实现FFT变换
Matlab实现FFT变换 文章目录Matlab实现FFT变换原理实现手算验证简单fft变换和频谱求取功率谱结论在信号处理中,快速傅里叶变换(FFT)是一种非常常见的频域分析方法。本文将介绍如何使用Matlab实现FFT变换,并通过Matlab代码演示实际…...
JVM调优面试题——垃圾回收专题
文章目录1、如何确定一个对象是垃圾?1.1、引用计数法1.2、可达性分析2、对象被判定为不可达对象之后就“死”了吗?3、都有哪些垃圾收集算法?3.1、 标记-清除(Mark-Sweep)3.2、标记-复制(Mark-Copying)3.3、标记-整理(Mark-Compact)3.4、分代收…...
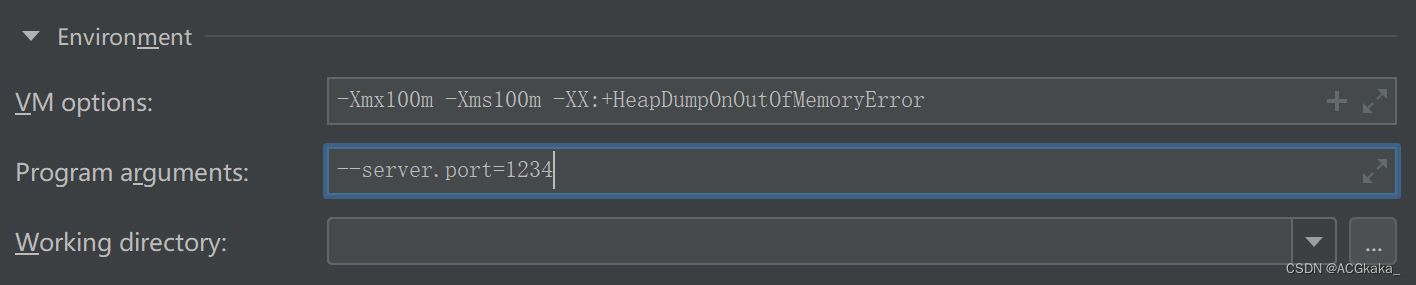
java启动命令中-D和--的区别
目录一、java -D 添加参数二、java -- 添加参数在 SpringBoot 项目中,启动时,通过 -D 或 -- 添加参数,都可以直接覆盖 yml 或 properties 配置文件中的同名配置,如果不存在则相当于添加了一个配置。 一、java -D 添加参数 java -D…...

QML Popup详解
1.简介 弹出式用户界面控件,它可以与Window或ApplicationWindow一起使用,默认不可见。 常用属性介绍,一些公用的基础属性就不作介绍,可以查看我前面写的文章。 closePolicy : enumeration :此属性决定弹出窗口关闭的…...
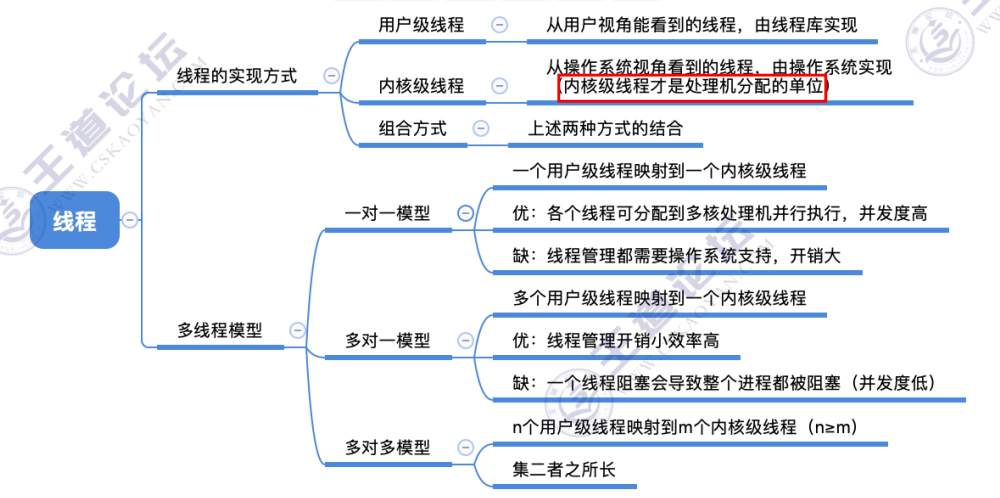
[2.1.6]进程管理——线程的实现方式和多线程模型
文章目录第二章 进程管理线程的实现方式和多线程模型一、线程的实现方式(一)用户级线程(二)内核级线程二、多线程模型(一)一对一模型(二)多对一模型(三)多对多…...

小白做什么兼职项目赚钱?宝妈拍短视频赚钱的方法
很多宝妈在家带孩子之余想做兼职赚点小钱,依靠互联网无疑是比较方便的途径,在刷单、微商等网上兼职成为过去式以后,很多宝妈选择了短视频创业。 宝妈怎么拍短视频? 宝妈因为要照顾宝宝还要兼顾家务,空闲的时间比较琐碎…...
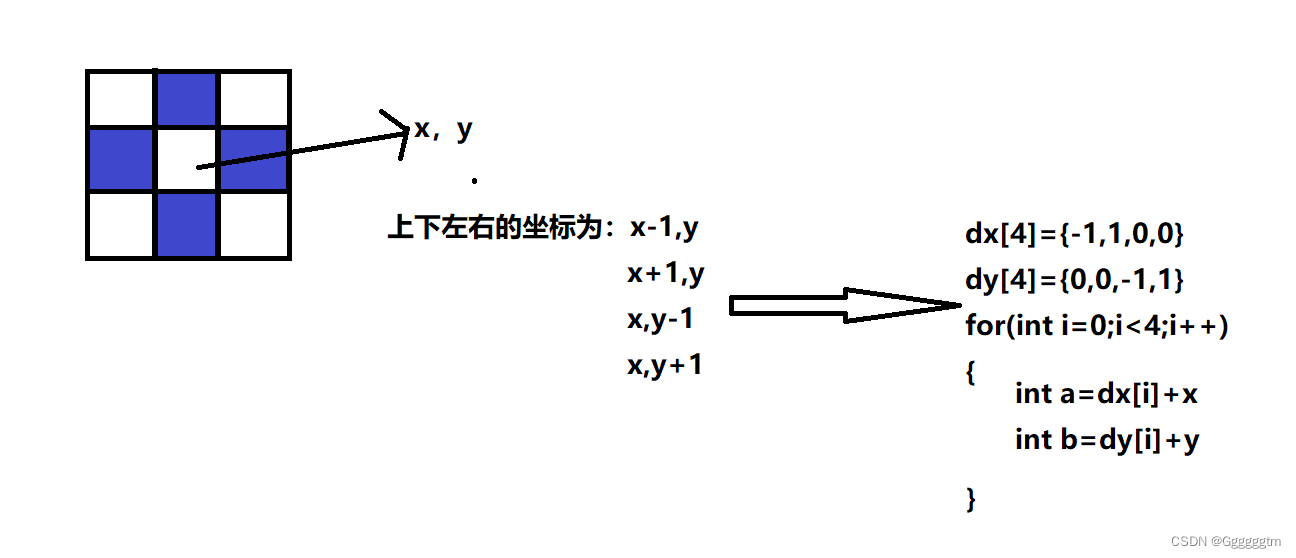
第十四届蓝桥杯第三期模拟赛 C/C++ B组 原题与详解
文章目录 一、填空题 1、1 找最小全字母十六进制数 1、1、1 题目描述 1、1、2 题解关键思路与解答 1、2 给列命名 1、2、1 题目描述 1、2、2 题解关键思路与解答 1、3 日期相等 1、3、1 题目描述 1、3、2 题解关键思路与解答 1、4 乘积方案数 1、4、1 题目描述 1、4、2 题解关…...

Linux中断操作
一、thread_irq在内核中, 除了可以通过request_irq() 、 devm_request_irq()申请中断以外, 还可以通过以下二个函数申请( 它们比request_irq和devm_request_irq多了一个参数thread_fn)。 用这两个API申请中断的时候, 内核会为相应的中断号分配…...

看看CabloyJS是如何异步加载并执行go wasm模块的
介绍 CabloyJS提供了一个内置模块a-wasmgo,将go wasm模块的异步加载运行机制进行了封装,使我们可以非常方便的在CabloyJS项目中引入go wasm,从而支持更多的业务场景开发 下面,我们以测试模块test-party为例,演示引入…...
嵌入式C语言九大数据结构操作方式详解
在C语言的开发过程中,灵活使用数据结构,对提高编程效率有极大的帮助。 目录 1 数组 2 链表 3 跳表 4 栈 5 队列 6 树 7 堆 8 散列表 9 图 10 总结 数据结构想必大家都不会陌生,对于一个成熟的程序员而言,熟悉和掌握数据…...

【C++学习】栈 | 队列 | 优先级队列 | 反向迭代器
🐱作者:一只大喵咪1201 🐱专栏:《C学习》 🔥格言:你只管努力,剩下的交给时间! 栈 | 队列 | 优先级队列 | 反向迭代器😼容器适配器🙈什么是适配器ὤ…...

Python—看我分析下已经退市的 可转债 都有什么特点
分析 需求分析 可转债退市原因的种类与占比是多少 强赎与非强赎导致的退市可转债 存续时间 维度占比 强赎与非强赎导致的退市可转债 发行资金 规模占比 强赎与非强赎导致的退市可转债 各个评级 的占比 强赎与非强赎导致的退市可转债 各个行业(一级行业…...

【第八课】空间数据基础与处理——数据结构转化
一、前言 数据结构即指数据组织的形式,是适合于计算机存储、管理和处理的数据逻辑结构。对空间数据则是地理实体的空间排列方式和相互关系的抽象描述。它是对数据的一种理解和解释,不说明数据结构的数据是毫无用处的,不仅用户无法理解,计算机程序也不能正确地处理,对同样一组数…...

MATLAB绘制三Y轴坐标图:补充坐标轴及字体设置
三轴坐标图 1 函数 MATLAB绘制三轴图函数可见MATLAB帮助-multiplotyyy 基础图形绘制是很简单,但坐标轴及字体设置该如何实现呢? 本文以以下几个例子为例,希望可以解决在利用MATLAB绘制三轴坐标图时常见的疑惑。 2 案例 2.1 案例1…...
springboot项目中Quartz
下面内容大家可在自己创建的 springboot项目中 玩1 定时清理垃圾图片定时任务组件Quartz,可以根据我们设定的周期,定时执行目标任务计划1.1 Quartz介绍(了解)Quartz是Job scheduling(作业调度)领域的一个开源项目&…...
Presto本地开发,plugin的设置
1. 新的问题 之前搭建Presto的本地开发环境时,一直使用config.properties中的plugin.bundles配置项定义需要加载的plugin模块,详细可以参考博客《win10基于IDEA,搭建Presto开发环境》presto服务启动时,指定加载哪些组件ÿ…...

2023年3月西安/杭州/深圳/东莞NPDP产品经理认证考试报名
产品经理国际资格认证NPDP是国际公认的唯一的新产品开发专业认证,集理论、方法与实践为一体的全方位的知识体系,为公司组织层级进行规划、决策、执行提供良好的方法体系支撑。 【认证机构】 产品开发与管理协会(PDMA)成立于1979年…...

Vue3笔记01 创建项目,Composition API,新组件,其他
Vue3 创建Vue3项目 vue-cli //查看vue/cli版本,确保在4.5.0以上 vue --version //安装或升级vue/cli npm install -g vue/cli //创建项目 vue create new_project //启动 cd new_project npm run serve 也可以通过vue ui进入图形化界面进行创建 vite 新一代前端…...
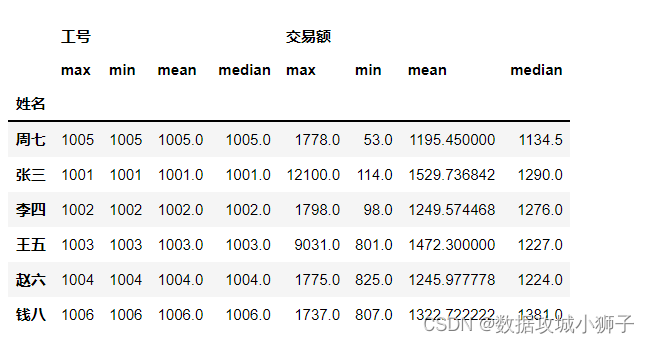
pandas数据分析(二)
文章目录DataFrame数据处理与分析读取Excel文件中的数据筛选符合特定条件的数据查看数据特征和统计信息按不同标准对数据排序使用分组与聚合对员工业绩进行汇总DataFrame数据处理与分析 部分数据如下 这个数据百度可以搜到,就是下面这个 读取Excel文件中的数据 …...

Spring实现[拦截器+统一异常处理+统一数据返回]
Spring拦截器 1.实现一个普通拦截器 关键步骤 实现 HandlerInterceptor 接口重写 preHeadler 方法,在方法中编写自己的业务代码 Component public class LoginInterceptor implements HandlerInterceptor {/*** 此方法返回一个 boolean,如果为 true …...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
