六西格玛项目的核心要素:理论学习、实践应用与项目经验
许多朋友担心,没有项目经验是否就意味着无法考取六西格玛证书。针对这一疑问,张驰咨询为大家详细解答。

首先,需要明确的是,六西格玛项目不仅仅是一种管理工具或方法,更是一种追求卓越、持续改进的思维方式。它强调通过数据分析、流程优化等方式,实现产品或服务质量的显著提升。因此,考取六西格玛证书更多的是考察你对这一理念的认同和理解,以及运用相关工具和方法的能力。
对于没有项目经验的朋友来说,这并不意味着你无法学习和掌握六西格玛。相反,你可以从理论学习入手,深入了解六西格玛的核心概念、流程(如DMAIC)和工具(如测量系统分析、失效模式与影响分析等)。这些理论知识是六西格玛项目的基石,掌握它们将为你后续的实践应用奠定坚实基础。
当然,理论知识的学习与实践应用的结合是至关重要的。即使你没有直接的项目经验,也可以寻找一些小型六西格玛项目或团队活动来实践六西格玛的方法。例如,你可以参与公司内部的质量改进项目、流程优化项目等,运用所学知识进行分析和改进。这样不仅能提升你的实践能力,还能为你的简历增添不少亮点。
因此,我们可以得出结论:没有项目经验并不是考取六西格玛证书的障碍。关键在于你是否愿意投入时间和精力去学习、去实践六西格玛项目、去追求卓越。只要你拥有这样的热情和决心,六西格玛的世界就会向你敞开大门。
最后,张驰咨询鼓励所有对六西格玛项目感兴趣的朋友,勇敢迈出那一步。无论你是初学者还是资深人士,我们都将为你提供最专业、最全面的咨询和培训服务。让我们一起在六西格玛项目的道路上不断前行,追求卓越、创造辉煌!
相关文章:

六西格玛项目的核心要素:理论学习、实践应用与项目经验
许多朋友担心,没有项目经验是否就意味着无法考取六西格玛证书。针对这一疑问,张驰咨询为大家详细解答。 首先,需要明确的是,六西格玛项目不仅仅是一种管理工具或方法,更是一种追求卓越、持续改进的思维方式。它强调通…...
)
21-ESP32-S3实时时钟(RTC)
ESP32-S3实时时钟(RTC)的使用 ESP32-S3是一款高性能的Wi-Fi和蓝牙集成的系统级芯片(SoC),它包含一个实时时钟(RTC)模块,可以在系统的其他部分关闭时继续运行,以节省电能…...
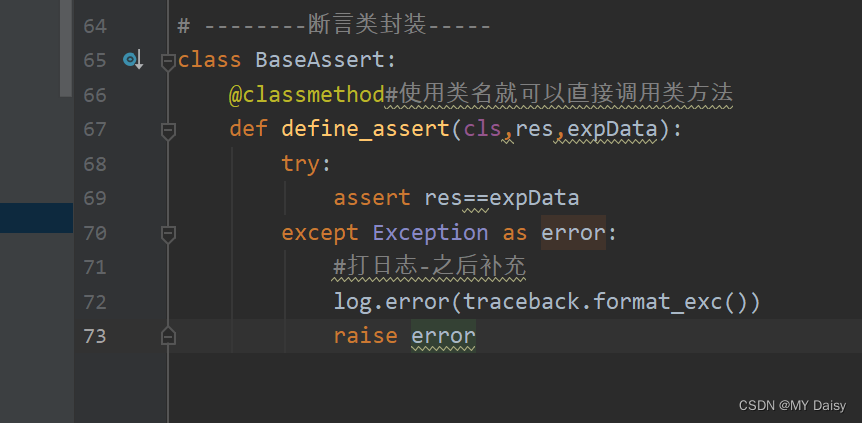
17.接口自动化学习-日志
1.日志输出渠道 (1)文件格式 xx.log (2)控制台输出 2.日志级别 debug<info<warnning<error<critical 3.代码实现 from utils.handle_path import log_path import logging import datetime def logger(fileLogTr…...

python直接发布到网站wordpress之二发布图片
在我的上一篇文章中已经给出了python操作wordpress的环境和发布文字的教程: python直接发布到网站wordpress之一只发布文字-CSDN博客 本篇实现发布带图片的内容,无图无真相嘛。 直接上代码: from wordpress_xmlrpc.methods.media import …...
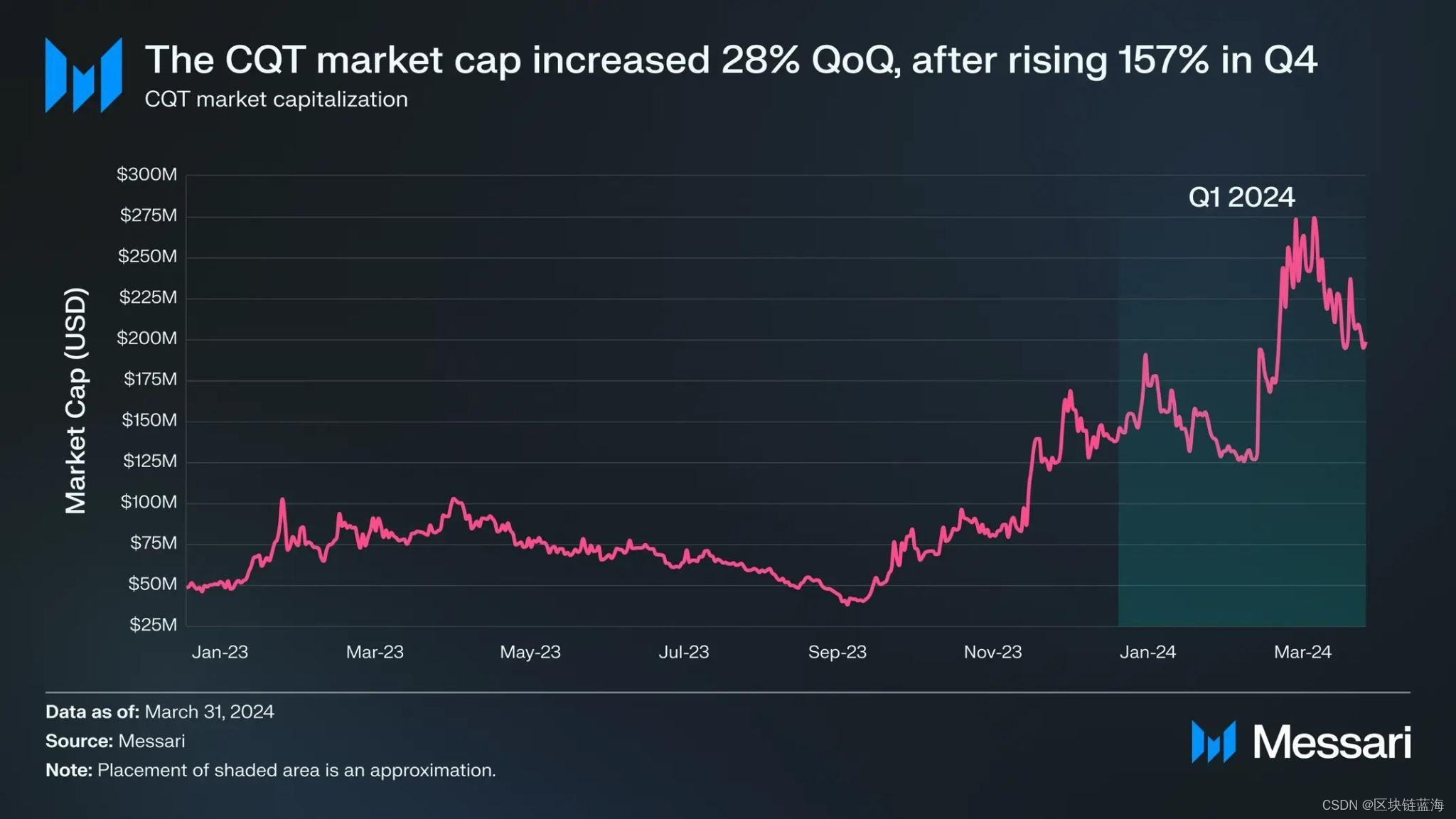
Messari 报告摘要 :Covalent Network(CQT)2024 年第一季度表现
摘要: 尽管 CQT 代币流通供应量增加了 20%(新增 1.04 亿枚 CQT),但 CQT 的质押百分比仅从 2023 年第一季度的 22% 增长到了 2024 年第一季度的 29%。 CQT 的市值季度环比增长了 28%,多次达到 2.75 亿美元,…...

PGP加密技术:保护信息安全的利器
随着数字化时代的到来,个人和企业对信息安全的需求日益增长。PGP(Pretty Good Privacy)加密技术作为一项强大的加密工具,为保护敏感数据提供了一种有效的方法。本文将探讨PGP加密技术的基本原理、应用场景以及其在现代信息安全中的…...
【C++】文件
目录 文件文件分类文本文件的读写(ASCII文件)的读写打开文件打开文件的方式关闭文件将数据写入ASCII文件从ASCII文件读入数据 二进制存储对比ASCII和二进制存储用成员函数read和write读写二进制文件打开方式文件的读入与读出 文件 所谓文件,一般指存储在外部介质上…...
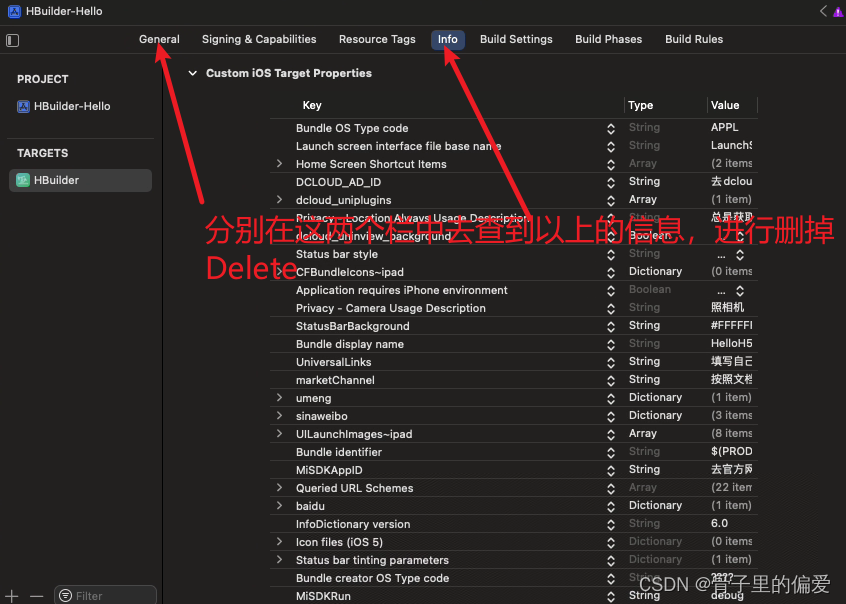
uniapp离线在Xcode上打包后提交审核时提示NSUserTrackingUsageDescription的解决方法
uniapp离线在Xcode上打包后提交审核时提示NSUserTrackingUsageDescription的解决方法 问题截图: 亲测有效的方法 方法一: 选择通过uniapp的开发工具Hbuilder来进行在线打包,取消默认勾选的以下选项。 然后进行在线打包就不会存在提交审…...
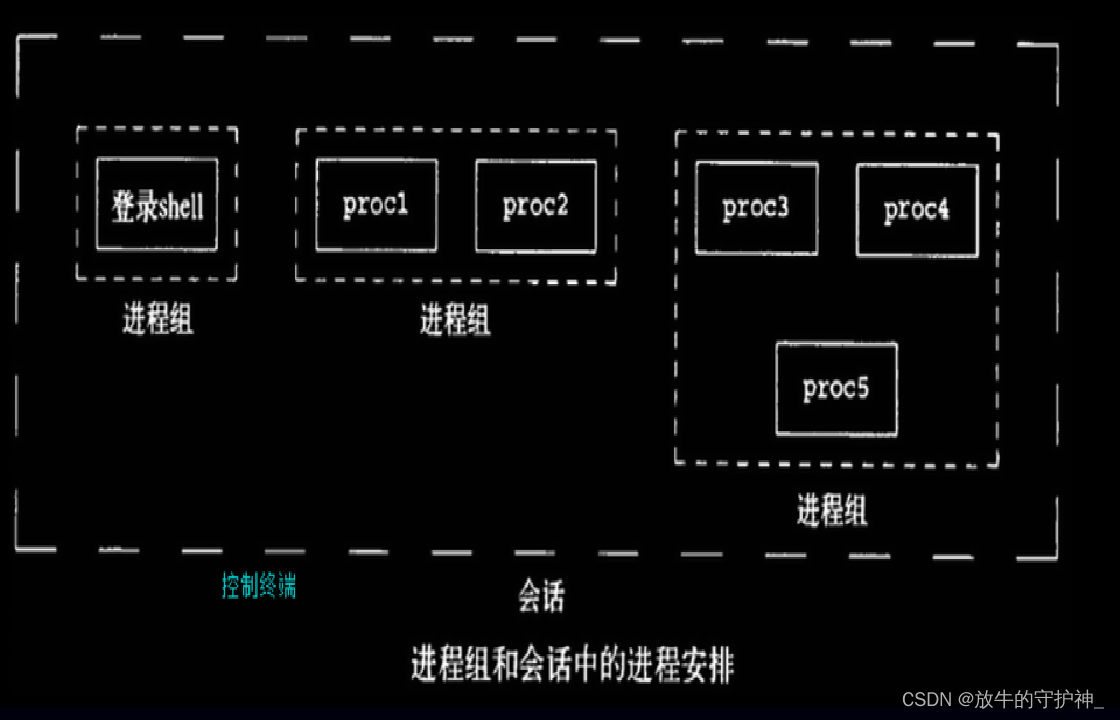
【Linux】进程exec函数族以及守护进程
一.exec函数族 1.exec函数族的应用 在shell下敲shell的命令都是在创建shell的子进程。而我们之前学的创建父进程和子进程代码内容以及通过pid与0的关系来让父子进程执行不同的代码内容都是在一个代码文件里面,而shell是如何做到不在一个文件里面写代码使之成为子进…...

为什么 ChatGPT 不火了?
不火了是有原因的,下面我来从大部分人拿到 ChatGPT 之后的两大痛点开始讲起: 很多朋友拿到 ChatGPT 后的第一个痛点就是:用的不好 你经常会感觉到 ChatGPT 回答的好空,没有太多参考价值。 而第二个痛点则是:无处去用…...

Ubuntu22.04下安装kafka_2.11-0.10.1.0并运行简单实例
目录 一、版本信息 二、安装Kafka 1.将Kafka安装包移到下载目录中 2.下载Spark并确保hadoop用户对Spark目录有操作权限 三、启动Kafka并测试Kafka是否正常工作 1.启动Kafka 2.测试Kafka是否正常工作 一、版本信息 虚拟机产品:VMware Workstation 17 Pro 虚…...

【S32K3 MCAL配置】-7.2-GPT Driver:仿OS,周期/定时调用APP SWC和BSW模块的主函数
"><--返回「Autosar_MCAL高阶配置」专栏主页--> 案例背景:当没有移至FreeRTOS时,如何仿OS,快速搭建“若干个周期执行的Task”,在其中周期/定时调用APP SWC和BSW模块的主函数。 并在这个简易的仿OS中,如何设置“主函数调用的先后顺序”,以及如何设置“主函…...

golang内置包里面的sort.Slice 切片排序函数使用示例
go语言里面用的最多的数据类型应该是切片Slice了, 今天就给大家介绍这个go内置包里面的切片排序函数的使用方法 函数原型 func Slice(x any, less func(i, j int) bool) 参数说明 这个函数有2个参数, 第一个是你要进行排序的slice切片,地个…...

Golang | Leetcode Golang题解之第70题爬楼梯
题目: 题解: func climbStairs(n int) int {sqrt5 : math.Sqrt(5)pow1 : math.Pow((1sqrt5)/2, float64(n1))pow2 : math.Pow((1-sqrt5)/2, float64(n1))return int(math.Round((pow1 - pow2) / sqrt5)) }...

区块链 | NFT 相关论文:Preventing Content Cloning in NFT Collections(三)
🐶原文: Preventing Content Cloning in NFT Collections 🐶写在前面: 这是一篇 2023 年的 CCF-C 类,本博客只记录其中提出的方法。 F C o l l N F T \mathbf{F_{CollNFT}} FCollNFT and Blockchains with Native S…...
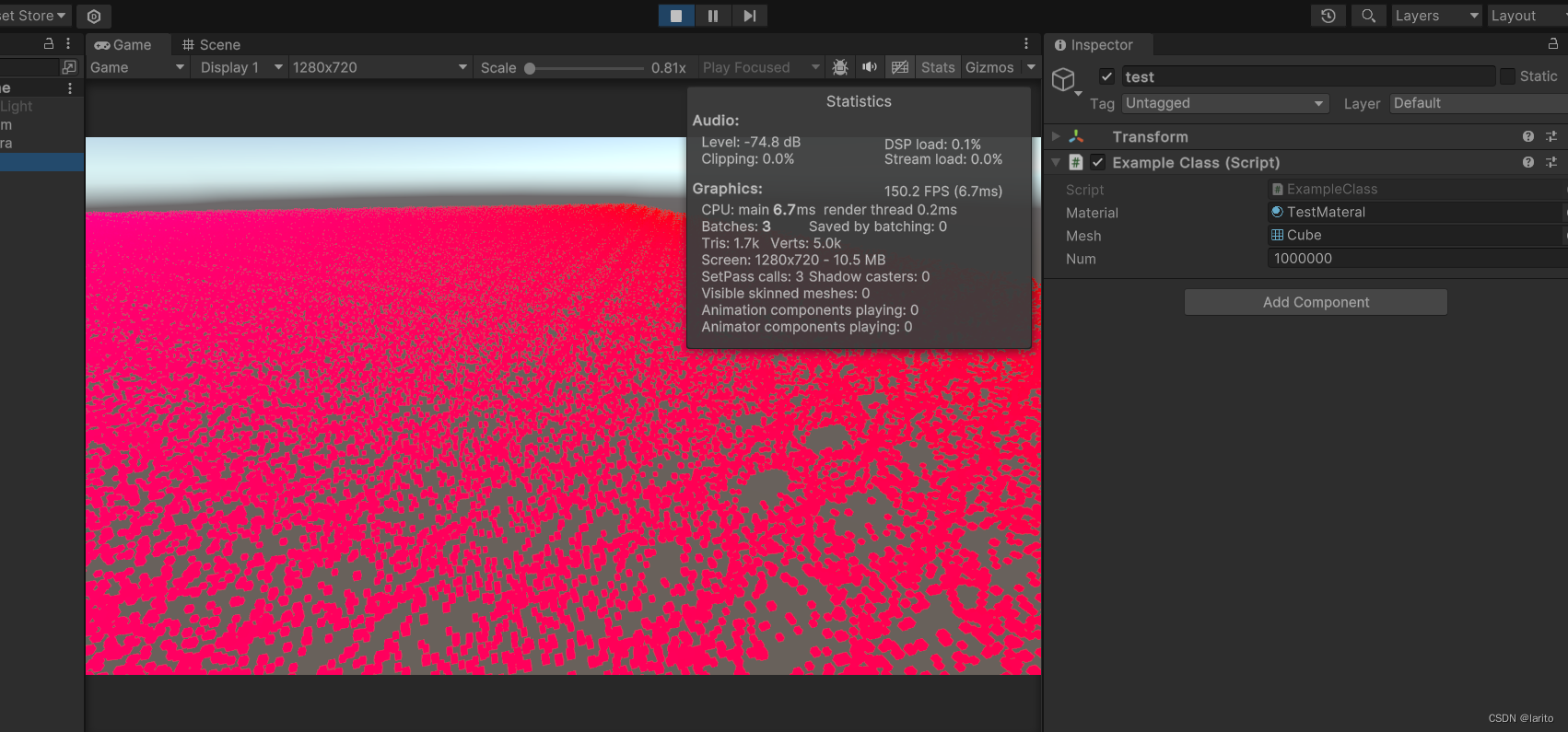
Unity技术学习:渲染大量物体的解决方案,外加RenderMesh、RenderMeshInstanced、RenderMeshIndirect的简单使用
叠甲:本人比较菜,如果哪里不对或者有认知不到的地方,欢迎锐评(不玻璃心)! 导师留了个任务,渲染大量的、移动的物体。 寻找解决方案: 当时找了几个解决方案: 静态批处…...

[数据概念|方案实操][最新]数据资产入表4月速递
“ 在各地数据资产变现“热辣滚烫”” 国家数据局全国数据工作会议前后,数据资源“入表”的尝试在各地持续热火朝天地展开,多地实现数据资产入表和利用数据资产进行融资实现“零的突破”。 我们今天就把4月前后的案例做一个小结,之前的案例大…...

C++中使用Multimap和Vector管理和展示数据
一: 在本文中,我们将探讨如何在C中使用vector和multimap容器来管理一个简单的员工数据系统。我们将创建一个员工类,随机生成员工数据,将员工分组,并展示各组员工的详细信息。此示例展示了C标准模板库(STL&…...

Java---类和方法的再学习
上一篇主要介绍了面向对象的思想以及内存实现,关于类与对象感觉写的不够好,因此才会有这一篇作为补充; 一:类与对象 (1)类 一些相同属性和行为的事物的统称,比较广泛、抽象,比如…...
)
C语言每日一练(12、水仙花数)
在编程的领域中,我们常常会遇到一些有趣而富有挑战性的问题。今天,让我们一起来探讨一个经典的编程题目——打印出所有的“水仙花数”。 所谓“水仙花数”,是指一个三位数,其各位数字的立方和等于该数本身。例如,153 …...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
