堆的应用2——TOPK问题
TOPK问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
情况1——数据量小
对于Top-K问题,能想到的最简单直接的方式就是排序,
就是我们建N个数的大堆,再Pop K次就行了
代码展示(最大的K个)
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
#include<string.h>
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType x = *p1;*p1 = *p2;*p2 = x;
}//堆的向下调整(大堆)
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1; // 计算左子节点的索引 // 当 child 索引在数组范围内时执行循环 while (child < n){// 如果右子节点存在且大于左子节点 if (child + 1 < n && a[child + 1] > a[child]){++child; // 更新 child 为右子节点的索引 }// 如果 child 节点(现在是左右子节点中较大的一个)大于 parent 节点 if (a[child] > a[parent]){Swap(&a[child], &a[parent]); // 交换 parent 和 child 的值 parent = child; // 更新 parent 为刚刚交换过的 child 的索引 child = parent * 2 + 1; // 重新计算左子节点的索引 }else{break; // child 节点不大于 parent 节点,无需继续调整,退出循环 }}
}void HeapInit(HP* php)
{assert(php);php->a = (HPDataType*)malloc(sizeof(HPDataType) * 4);if (php->a == NULL){perror("malloc fail");return;}php->size = 0;php->capacity = 4;
}bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}// 除了child这个位置,前面数据构成堆
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//while (parent >= 0)while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity *= 2;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}//打印堆
void HeapPrint(HP* php)
{assert(php);//按照物理结构进行打印int i = 0;for (i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));// 删除数据Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}HPDataType HeapTop(HP* php)
{assert(php);return php->a[0];
}int HeapSize(HP* php)
{assert(php);return php->size;
}int main()
{HP hp;HeapInit(&hp);HeapPush(&hp, 4);HeapPush(&hp, 180);HeapPush(&hp, 42);HeapPush(&hp, 12);HeapPush(&hp, 21);HeapPush(&hp, 3);HeapPush(&hp, 1);HeapPush(&hp, 2);HeapPush(&hp, 50);HeapPush(&hp, 5);HeapPush(&hp, 5);HeapPush(&hp, 150);HeapPush(&hp, 5);HeapPush(&hp, 45);HeapPush(&hp, 5);int k = 0;scanf("%d", &k);while (!HeapEmpty(&hp) && k--){printf("%d ", HeapTop(&hp));HeapPop(&hp);}printf("\n");return 0;
}
情况2——数据量大
但是:如果数据量非常大,排序就不太可取了(可能 数据都不能一下子全部加载到内存中)。
最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前K个元素来建堆
- 前k个最大的元素,则建小堆
- 前k个最小的元素,则建大堆
有人就好奇了,为什么找最大的要建小堆而不是大堆,原因很简单,
建小堆,最大的K个元素肯定可以进去,但是如果建的是大堆的话,假设前K个里就遇到了最大的,它就会阻止后面其他次大的元素进去堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比,如果这个数据比堆顶的数据大,就替代它进堆,遍历完后堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
代码展示
代码分两步执行
我们先来看看源码
#include<stdio.h>
#include<time.h>
#include<stdlib.h>
#include<assert.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType x = *p1;*p1 = *p2;*p2 = x;
}//堆的向下调整(小堆)—— 左右子树都是小堆
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){// 选出左右孩子中大的那一个if (child + 1 < n && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void PrintTopK(const char* file, int k)
{// 1. 建堆--用a中前k个元素建小堆int* topk = (int*)malloc(sizeof(int) * k);assert(topk);FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen error");return;}// 读出前k个数据建小堆for (int i = 0; i < k; ++i){fscanf(fout, "%d", &topk[i]);}for (int i = (k - 2) / 2; i >= 0; --i){AdjustDown(topk, k, i);}// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换int val = 0;int ret = fscanf(fout, "%d", &val);while (ret != EOF){if (val > topk[0]){topk[0] = val;AdjustDown(topk, k, 0);}ret = fscanf(fout, "%d", &val);}for (int i = 0; i < k; i++){printf("%d ", topk[i]);}printf("\n");free(topk);fclose(fout);
}void CreateNDate()
{// 造数据int n = 10000000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (size_t i = 0; i < n; ++i){int x = rand() % 10000;fprintf(fin, "%d\n", x);}fclose(fin);
}第一步创建数据
int main()
{CreateNDate();return 0;
}我们先运行一下上面的代码,然后就能在目录下看到我们创建了一个txt文件
这里就有我们要的超大量数据,我们可以把它添到目录下来,方便修改
我们创建的都是10000以内的数据,
第二步——修改数据
int main()
{PrintTopK("data.txt",10);return 0;
}我们先运行一下

确认都在10000内之后,就去修改数据
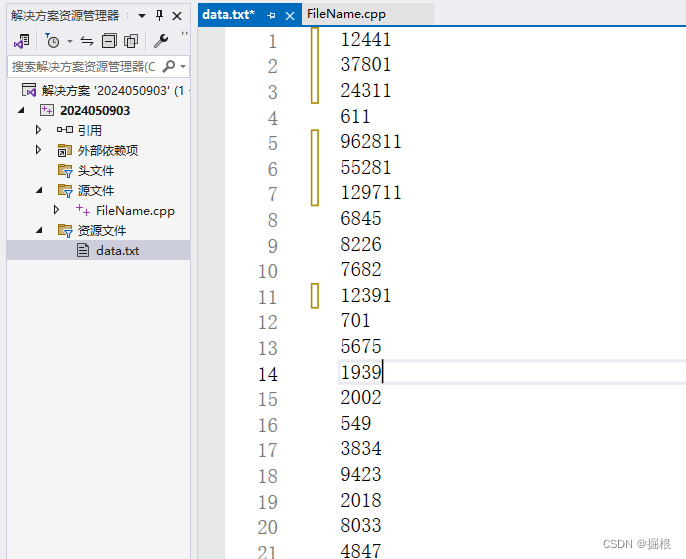
再运行上面的代码,得到下面结果

我们发现,修改后的7个数据全在里面,也就说明我们的代码没有问题
相关文章:

堆的应用2——TOPK问题
TOPK问题 TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。 比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。 情况1——数据量小 对于Top-K问题,能想到的最简单直接的方式就…...

leetcode-5. 最长回文子串
题目描述 给你一个字符串 s,找到 s 中最长的回文子串。 如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。 示例 1: 输入:s "babad" 输出:"bab" 解释:"aba"…...

【Flask 系统教程 1】入门及配置
当你开始学习 Flask 时,了解如何进行基本的配置是非常重要的。Flask 是一个简单而灵活的 Python Web 框架,它允许你快速构建 Web 应用程序,并且易于学习。在这篇博客中,我将介绍如何从零开始进行 Flask 的基础配置,适合…...

石家庄河北银行的
有些时候河北石家庄这边的甲方客户人员就是太苛刻了,尤其是银行业 比如河北银行的信息部的卢斌,兰州人,这个人的人品极度恶劣,对乙方的外包人员特别苛刻,像个大爷一样。自己什么都不会,连sql 都不会写&…...
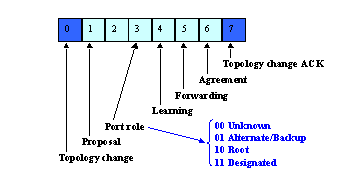
【CCNP ENCOR OCG】CHAPTER 2》Spanning Tree Protocol
目录 “Do I Know This Already?” Quiz Foundation Topics Spanning Tree Protocol Fundamentals 802.1D Port States Spanning Tree Path Cost Root Bridge Election Locating Root Ports Locating Blocked Designated Switch Ports Verification of VLANs on Trun…...

docker无法映射/挂载根目录
docker无法映射(挂载)根目录下的文件夹只能映射家目录 最近想要使用nas-tools做做刮削,电影存在一个机械磁盘里,机械磁盘被挂载到/data1下,发现一个很奇怪的问题,docker只能挂载成功home目录下的文件夹&am…...

C++中不要重新定义继承而来的non-virtual函数
在 C 中,重定义继承而来的 non-virtual(非虚)函数通常是不推荐的,原因如下: 隐藏父类的实现:如果在派生类中重定义了一个非虚函数,这将隐藏父类中具有相同名称和参数的函数。这意味着即使通过基…...
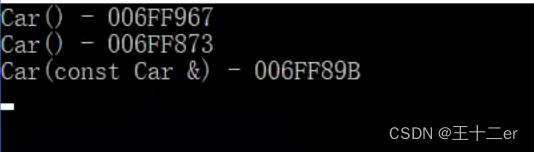
C++ 对象型参数和返回值
对象型参数和返回值 1.对象型类型作为函数的参数2.对象型参数作为函数的返回值 1.对象型类型作为函数的参数 使用对象类型作为函数的参数或者返回值,可能会产生一些不必要的中间对象 例子: // 使用对象类型作为函数的参数 void test1(Car car) {}完整代…...

LeetCode 字符串专题——KMP算法_28. 找出字符串中第一个匹配项的下标
字符串专题——KMP算法 KMP算法例题 KMP算法 待更新 例题 https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/description/ class Solution {vector<int> next;void getNext(string s){int j-1;next[0]-1;int lens.size();for(int i…...
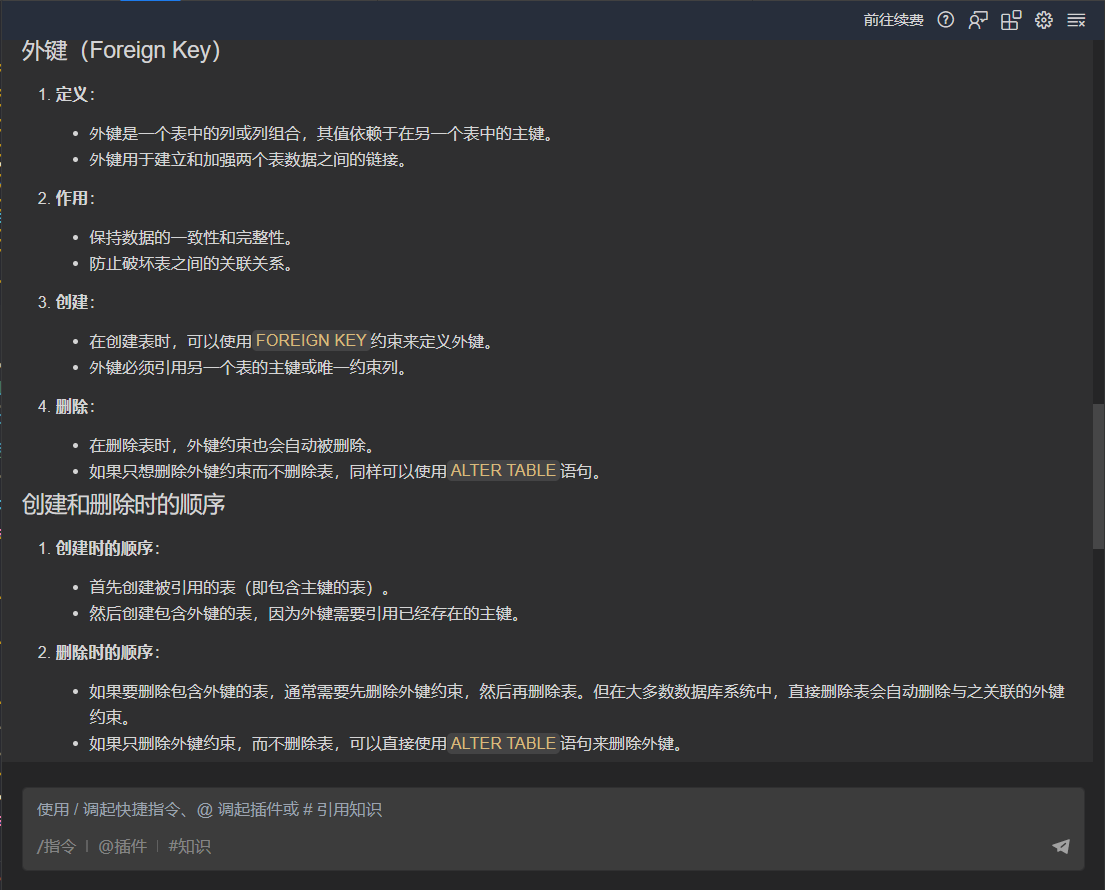
上班不想用脑子写代码了怎么办?那就试试Baidu Comate啊宝贝
本文目录 前言1、视频编程实战1.1、熟悉代码库中的代码1.2、参考现有代码编写新代码 2、下载使用教程3、使用体验3.1、AutoWork 产品测评3.2、解决有关ajax请求后重定向问题3.3、询问编程相关知识3.3.1、cookie和session的区别与联系3.3.2、数据库中主键外键的相关知识 4、问题…...

【管理咨询宝藏94】某国际咨询公司供应链财务数字化转型方案
本报告首发于公号“管理咨询宝藏”,如需阅读完整版报告内容,请查阅公号“管理咨询宝藏”。 【管理咨询宝藏94】某国际咨询公司供应链&财务数字化转型方案 【格式】PDF版本 【关键词】国际咨询公司、制造型企业转型、数字化转型 【核心观点】 - 172…...
实现有向图[完整示例及解释])
C++_使用邻接表(链表-指针)实现有向图[完整示例及解释]
这个程序是一个图的实现,使用邻接表来表示图的结构: 1. 结构定义部分: - AdjListNode 结构定义了邻接表中的节点,每个节点包含一个名称和一个指向下一个邻接节点的指针。 - Node 结构定义了图中的节点,每个节点…...
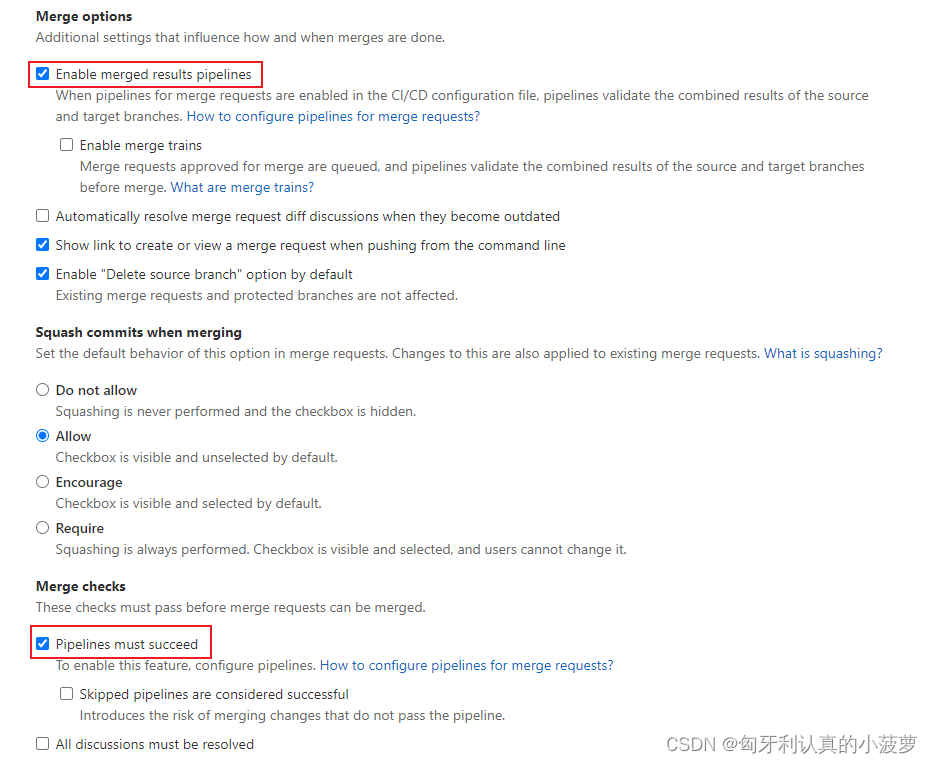
Gitlab自动化测试的配置
1. 代码分支命名规范检测 Setting → Repository → Push rules → Branch name,添加分支命名规范对应的正则表达式。如: ^(Release|Tag|Develop|Feature)_._.|Main$ 表示分支名只能以以下关键字之一开头:Release、Tag、Develop和Feature。 …...

Qwen-Audio:推动通用音频理解的统一大规模音频-语言模型(开源)
随着人工智能技术的不断进步,音频语言模型(Audio-Language Models)在人机交互领域变得越来越重要。然而,由于缺乏能够处理多样化音频类型和任务的预训练模型,该领域的进展受到了限制。为了克服这一挑战,研究…...

杭州破冰之举:全面取消住房限购,激发市场新活力
在房地产市场调控的浪潮中,杭州再次走在了前列,于2024年3月14日宣布全面取消二手房限购政策,此举在行业内引发了广泛关注。作为中国经济活力较强的二线城市之一,杭州的这一决策不仅体现了地方政府在房地产市场调控上的灵活应变,也释放出对市场流动性和经济发展的积极信号。…...

ICode国际青少年编程竞赛- Python-1级训练场-变量练习
ICode国际青少年编程竞赛- Python-1级训练场-变量练习 1、 a 8 for i in range(8):Dev.step(a)Dev.turnRight()a - 12、 a 3 for i in range(4):Dev.step(a)Dev.turnRight()a a 1 Dev.step(5)3、 a 4 for i in range(4):Dev.step(2)Dev.step(-5)Dev.step(3)Spaceship.…...

学习STM32第二十天
低功耗编程 一、修改主频 STM32F4xx系列主频为168MHz,当板载8MHz晶振时,系统时钟HCLK满足公式 H C L K H S E P L L N P L L M P L L P HCLK \frac{HSE \times PLLN}{PLLM \times PLLP} HCLKPLLMPLLPHSEPLLN,在文件stm32f4xx.h中可修…...
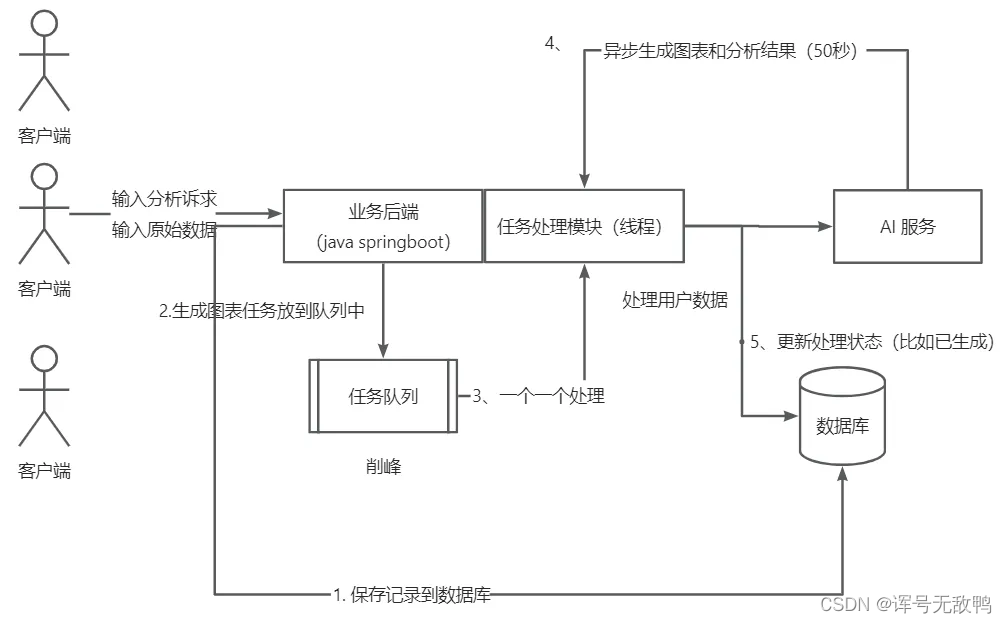
智能BI(后端)-- 系统异步化
文章目录 系统问题分析什么是异步化?业务流程分析标准异步化的业务流程系统业务流程 线程池为什么需要线程池?线程池两种实现方式线程池的参数线程池的开发 项目异步化改造 系统问题分析 问题场景:调用的服务能力有限,或者接口的…...

AI绘画Stable Diffusion 插件篇:智能标签提示词插件sd-danbooru-tags-upsampler
大家好,我是向阳。 关于智能标签提示词插件,在很早之前就介绍过很多款了,今天再给大家介绍一款智能标签提示词插件sd-danbooru-tags-upsampler。该智能提示词插件是今年2月23号才发布的第一版V0.1.0,算是比较新的智能提示词插件。…...
OMXStore)
Android OpenMAX(六)OMXStore
在前面两节的学习中我们知道了OMX Core是用来管理(查询/创建/销毁)Android平台上的硬件编解码组件的。这一节我们再向上一层,Android平台除了提供有硬件编解码组件支持,还内置了一些软件编解码组件,为了统一管理所有(软/硬)编解码组件,Android在OMX Core之上又抽象了一…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
