刷题记录2
文章目录
- 刷题记录2
- 1047.删除字符串中的所有相邻重复项
- 150.逆波兰表达式求值
- 239.滑动窗口最大值
- 347.前k个高频元素
- 144.二叉树前序遍历(145、94后序、中序)
- 102.二叉树的层序遍历
- 226.翻转二叉树
- 101.对称二叉树
- 104.二叉树的最大深度
- 111.二叉树的最小深度
- 222.完全二叉树的节点个数
刷题记录2
1047.删除字符串中的所有相邻重复项
class Solution {
public:string removeDuplicates(string s) {string res = "";for(char a : s){if(res.empty() || res.back() != a) res.push_back(a);else if(res.back() == a) res.pop_back();}return res;}
};
像这种消消乐类型的题目都是用到的栈这种数据结构来解决问题,而这里呢是将string来代替栈,就不需要用到stack容器,如果使用stack容器还需要将容器内的元素重新遍历赋值到string中,然后还需要一次reverse反转,如果直接使用string作为栈就节省了代码和时间。这里在解题的时候遇到了一个空间性能上的一个问题,就是我将res.push_back(a)改成了res = res+a这种写法会导致内存超限,并且耗时将近500ms。我就在像这是为什么呢?两个操作明明都是在字符串尾部添加字符a,为什么空间和时间性能就相差这么大呢?通过搜索得知:res = res+a这种操作是会重新生成一个string临时变量,先将原本的res拷贝到临时变量中再添加上a再返回给res,这个操作又是在循环当中,假如题目中给出的s十分长,那么就相当于是On^2的时间复杂度了,再加上每个循环开辟一个临时变量,所以空间消耗也十分大。对于res.push_back来说它仅仅只是在res的基础上在后面添加字符a,这样要比运算符+要节省空间和时间很多。所以在遇到对字符串进行添加或删除时最好用push_back和pop_back。其他相关函数front(), back(), append()。
150.逆波兰表达式求值
class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> s;for(int i = 0; i < tokens.size(); i++){if(tokens[i] == "+"){int num1 = s.top();s.pop();s.top() += num1;}else if(tokens[i] == "-"){int num1 = s.top();s.pop();s.top() -= num1;}else if(tokens[i] == "*"){int num1 = s.top();s.pop();s.top() *= num1;}else if(tokens[i] == "/"){int num1 = s.top();s.pop();s.top() /= num1;}else s.push(stoi(tokens[i]));}return s.top();}
};
这一题其实只要读懂题目的意思就行了,然后按照题目给的要求编程就行了,关键是要明白这个题要用栈来写,看到提示:遇到数字则入栈,遇到运算符则取出栈顶两个数字进行计算,并将结果压入栈中,这里着重强调一下一个数字字符串转换数字的方法:int num = stoi(“12345”);但是呢,好像int num = "12345"也是能实现的,都记住吧,技多不压身。。。
239.滑动窗口最大值
class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {vector<int> ans;deque<int> dq;for(int i = 0; i < nums.size(); i++){//入while(!dq.empty() && nums[i] >= nums[dq.back()]) dq.pop_back();dq.push_back(i);//出if(i-dq.front() >= k) dq.pop_front();//记录数据if(i >= k-1) ans.push_back(nums[dq.front()]);}return ans;}
};
以前绝对遇到过这种题!我记得当时我单纯用for循环嵌套都写不出来着,现在至少能用for循环嵌套能够写出来了,当然如果暴力的话怎么可能解决力扣的困难题呢,果然不出意外的运行超时了。当然有提升是肯定的,加油!
这里用到的数据结构是单调队列,做这么多题下来好像确实没怎么写过队列的题目。这里用到的思想是维护一个单调的队列来记录nums[i]的值,这里题目求的是滑动窗口的最大值,那么我们就需要维护一个单调递减的一个队列,将最大的元素一直停留在队列的首位。首先是入队操作,循环判断队尾的元素是不是小于要插入进来的元素,如果尾元素小于要插入的元素的话就不断地将尾元素剔除,目的就在于使这个队列是递减的。然后就是出操作:插入元素后通过下标的循环不变量i-dq.front() >= k时就需要将首元素剔除掉。最后是记录数据操作,由于不同测试样例的窗口大小不同,所以前k个数据插入的时候是不需要记录数据的,所以当下标i=k-1的时候才开始记录结果。
347.前k个高频元素
144.二叉树前序遍历(145、94后序、中序)
递归法:
class Solution {
public:void preorder(TreeNode* root, vector<int>& res){if(root == nullptr) return;res.push_back(root->val);preorder(root->left, res);preorder(root->right, res);}vector<int> preorderTraversal(TreeNode* root) {vector<int> res;preorder(root, res);return res;}
};
中序和后序的递归方法还是很简单的,就是分别将res.push_back(root->val);放到两个递归函数的中间和后面,这样就分别达到了中序遍历和后序遍历的效果。
迭代法:
前序
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> s;vector<int> res;if(root == nullptr) return {};s.push(root);while(!s.empty()){TreeNode* temp = s.top();s.pop();res.push_back(temp->val);if(temp->right) s.push(temp->right);if(temp->left) s.push(temp->left);}return res;}
};
首先回顾前序遍历,它的递归方式是中左右。这样就不难写出前序遍历的递归写法。题目中的提升中给出要写出其迭代写法,最开始还是没有思路的,甚至想到的是用队列这种数据结构,但是经过脑袋一次思考之后回想起用队列的话是实现树的层序遍历,这并不能达到前中后序遍历的效果。看了一眼题解发现用的是栈,而且在使用栈的时候也是有需要注意的点:首先是入栈要判断树是否为空树,再就是入栈顺序,这里是右子树先入栈,左子树后入栈,由于栈是先入后出,所以是先右后左,还有就是入栈前需要对左右节点进行判空操作,如果为空那么就不能入栈,如果入栈了的话会导致空指针异常。
后序
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> s;vector<int> res;if(root == nullptr) return {};s.push(root);while(!s.empty()){TreeNode* temp = s.top();res.push_back(temp->val);s.pop();if(temp->left) s.push(temp->left);if(temp->right) s.push(temp->right);}reverse(res.begin(), res.end());return res;}
};
最开始想借着前序遍历的写法来写后序遍历,结果还是卡住了,卡尔给出的方法也实在是妙啊,前序遍历是中左右,而后序遍历是左右中,它采用的方法就是在指针入栈方面进行了改动,先将左右指针入栈的顺序颠倒了一下,就使结果变成了中右左,然后将res数组进行翻转就变成了最后的左右中,我天,这是人能想出来的办法吗555,真的佩服!
中序
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {stack<TreeNode*> s;vector<int> res;TreeNode* cur = root;while(!s.empty() || cur != nullptr){if(cur != nullptr){s.push(cur);cur = cur->left;}else{cur = s.top();s.pop();res.push_back(cur->val);cur = cur->right;}}return res;}
};
中序和其他两个差别还是很大的,主要难点在于用栈来模拟递归的逻辑这一点第一次来写确实有点难写,这方面还是有点薄弱,虽说考试不可能考迭代法写二叉树遍历、但这也是考试和以后面试的两手准备吧!
102.二叉树的层序遍历
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {deque<TreeNode*> dq;vector<vector<int>> res;if(root == nullptr) return {};dq.push_back(root);while(!dq.empty()){int n = dq.size();vector<int> temp;for(int i = 0; i < n; i++){TreeNode* tmp = dq.front();dq.pop_front();temp.push_back(tmp->val);if(tmp->left) dq.push_back(tmp->left);if(tmp->right) dq.push_back(tmp->right);}res.push_back(temp);}return res;}
};
这也是第二次做这道题了,唉又没做出来,还是忘得快啊,这才过了一个多月的题,就忘得一干二净了,当时在思考的时候还是想到的是以前自己的思路,就是没有回忆到以前题解的思路。这一题的层序遍历与其他不同点就在于每层的数据是一个一维数组,然后最后的结果是一个二维数组。其实感觉自己也是把题目想复杂化了,其实就是层多少个元素就将每层的元素传入到临时的一维数组中,多少个元素直接用dq.size()就能获取到。唉,给我最大的感觉就是还得回头看,重点的确不是在于多,还是在于你要掌握这个方法。
226.翻转二叉树
class Solution {
public:void reverse(TreeNode* root){if(root == nullptr) return;swap(root->left, root->right);if(root->left) reverse(root->left);if(root->right) reverse(root->right);}TreeNode* invertTree(TreeNode* root) {reverse(root);return root;}
};最开始我想着能不能取巧只交换节点的值是否能够达到效果,答案是不能,不能被题干中的示例给迷惑了,可能出现问题的情况是一个节点可能只有左右子树中的一个,这样就不能够通过交换左右节点的值来达到交换的效果,会出现空指针异常的错误。所以这里只能够用交换指针来达到目的,最开始我也对交换完指针之后是否会对后续递归产生问题产生疑惑,其实是不会的,无论是左右节点哪个先递归,最终目的是让所有其左右节点指针互换就行,所以只需要关注遍历整个树,这样就能达到我们最后想要的效果。
101.对称二叉树
class Solution {
public:bool isSame(TreeNode* p, TreeNode* q){//这一行包含了很多条件://1、左空右非空返回false//2、左非空右空返回false//3、左右都空返回trueif(p == nullptr || q == nullptr) return p == q;//左右都非空bool outside = isSame(p->left, q->right);bool inside = isSame(p->right, q->left);bool val = p->val == q->val;return val && outside && inside;}bool isSymmetric(TreeNode* root) {return isSame(root->left, root->right);}
};打开这一道题显示是1个月前做的题,现在一看,感觉跟新题没什么差别,唉还是没有思路。感觉前面跟灵神学做的算法题还是过于草率了,慢慢看出差别了,灵神讲题更注重于代码简洁和方法的灵活上面,这对于我们这种普通人来说接受起来只有那种昙花一现的效果,并不能将方法牢记于心,卡尔讲题确确实实落实在了干货上面,落在了基础上面,这才是真正的好讲师啊!
对于这一次提交的代码,我结合了灵神和卡尔的思路。首先对于递归退出的条件我只用一行解决了,但那一行代表的含义是丰富的,具体请看代码注释,再就是左右都非空的情况,这里就要用到后序遍历,为什么用后序遍历?卡尔给出的解释是:由于每一个节点都需要其孩子的真假信息才能判断当前节点的真假信息,需要将孩子的信息回溯到当前节点综合判断,所以用到的是后序遍历,解决二叉树问题无非就是四种遍历方式,但是具体采用哪一种一定要根据题意来采用,不同的遍历方式对于不同的题目产生的答案有可能不同,有时候一个题可以采用多种遍历方式,而有些题仅能采用某一种方式解题,这就是我之前刷题所遗漏的地方。最后解释一下val那一行,先进行的 == 运算,==运算的结果返回到val中,那一行也能写成bool val = p->val == q->val ? 1 : 0;还有就是return返回的值需要val、outside和inside综合判断真价值
这一道题给了我很大的感触吧,刷题确实不能图快,有时回过头来做的题其实又是一个新题。。。不能一个劲的追求简洁,扎实才是王道啊!
104.二叉树的最大深度
class Solution {
public:int func(TreeNode* root){if(root == nullptr) return 0;int leftNum = func(root->left);int rightNum = func(root->right);return max(leftNum, rightNum)+1;}int maxDepth(TreeNode* root) {return func(root);}
};这里给出二叉树的两个定义:深度:指节点到根节点的距离,根节点的深度为1;高度:节点到叶子节点的距离,叶子节点的高度为1。所以求深度最好是用前序遍历采用迭代方法比较好,但是写的话会比较麻烦,这里采用的是后序遍历,为什么会是后序遍历呢?题干求的是最大深度,那么是不是可以理解成求二叉树的最大高度呢?求最大高度也就是求根节点的高度,这样由叶子节点一步一步往上传递就用到的是后序遍历。
111.二叉树的最小深度
class Solution {
public:int minDepth(TreeNode* root) {if(root == nullptr) return 0;int leftnum = minDepth(root->left);int rightnum = minDepth(root->right);if(root->left == nullptr && root->right != nullptr) return 1+rightnum;else if(root->right == nullptr && root->left != nullptr) return 1+leftnum;else return min(leftnum, rightnum)+1;}
};整体上与前面一道题是相同的解法,也是用到的后序遍历的方法,但是再返回值上有一点不同,需要对二叉树的各种情况进行讨论,先是左空右不空的情况—>返回根节点右子树的最小深度+1、右空左不空与前面上一个情况相反,最后是都不空的情况,直接返回根节点的最小深度。
结合前面的对称二叉树的题目,我发现其实在一般情况你写完提交后不能通过全部样例时就需要考虑二叉树的几个特殊情况:左空右不空、左不空右空、左右都不空、左右都空。
222.完全二叉树的节点个数
方法一:
class Solution {
public:int countNodes(TreeNode* root) {if(root == nullptr) return 0;return countNodes(root->left) + countNodes(root->right)+1;}
};方法二:
class Solution {
public:int countNodes(TreeNode* root) {if(root == nullptr) return 0;TreeNode* p_left = root->left, *p_right = root->right;int leftDepth = 1, rightDepth = 1;while(p_left){leftDepth++;p_left = p_left->left;}while(p_right){rightDepth++;p_right = p_right->right;}if(leftDepth == rightDepth) return pow(2, leftDepth)-1;int leftNum = countNodes(root->left);int rightNum = countNodes(root->right);return leftNum+rightNum+1;}
};方法一用的普通的后序遍历求完全二叉树的个数,因为遍历了整棵树所以时间复杂度是On的,而方法二用到了题干给出的完全二叉树的性质,利用完全二叉树的性质使时间复杂度降低了。具体的逻辑:在递归到每个节点的时候写一段代码来判断以当前节点为根节点的二叉树是否为完全二叉树,如果是,直接将2^深度-1返回给上一级,如果不是那么就继续后序遍历该树。如何判断一个子树是否为完全二叉树?—>由于题目中给出的树一定是完全二叉树,那么我们只需要从当前节点定义两个指针,分别一直往左迭代和往右迭代直到指为空,迭代的过程中用两个int型的变量记录各自的深度,最后判断两个深度是否相等,如果相等那么这个子树就是完全二叉树,反之则不是。
相关文章:

刷题记录2
文章目录 刷题记录21047.删除字符串中的所有相邻重复项150.逆波兰表达式求值239.滑动窗口最大值347.前k个高频元素144.二叉树前序遍历(145、94后序、中序)102.二叉树的层序遍历226.翻转二叉树101.对称二叉树104.二叉树的最大深度111.二叉树的最小深度222.完全二叉树的节点个数 …...

【配置】Docker搭建JSON在线解析网站
一个python朋友需要,顺便做一下笔记 正常用菜鸟的就够了,点下面 JSON在线解析 云服务器打开端口8787 连接上docker运行 docker run -id --name jsonhero -p 8787:8787 -e SESSION_SECRETabc123 henryclw/jsonhero-webhttp://ip:8787访问 Github&…...

2024.5.2 —— LeetCode 高频题复盘
目录 151. 反转字符串中的单词129. 求根节点到叶节点数字之和104. 二叉树的最大深度101. 对称二叉树110. 平衡二叉树144. 二叉树的前序遍历543. 二叉树的直径48. 旋转图像98. 验证二叉搜索树39. 组合总和 151. 反转字符串中的单词 题目链接 class Solution:def reverseWords(s…...

ThreeJS:光线投射与3D场景交互
光线投射Raycaster 光线投射详细介绍可参考:https://en.wikipedia.org/wiki/Ray_casting, ThreeJS中,提供了Raycaster类,用于进行鼠标拾取,即:当三维场景中鼠标移动时,利用光线投射,…...
docker挂载数据卷-以nginx为例
目录 一、什么是数据卷 二、数据卷的作用 三、如何挂载数据卷 1、创建nginx容器挂载数据卷 2、查看数据卷 3、查看数据卷详情 4、尝试在宿主机修改数据卷 5、查看容器内对应的数据卷目录 6、 访问nginx查看效果 一、什么是数据卷 挂载数据卷本质上就是实…...

Docker-compose部署Fastapi项目
Docker-compose部署Fastapi、postgres、Redis、Nginx) 之前有写过使用容器部署的方式,这次尝试使用Docker-compose试一次大胆的尝试 使用容器的方式部署只是掌握这项技能的基础,在使用Docker-compose的过程中会有些稍许的不同。毕竟踩过的坑才算是跨过去…...
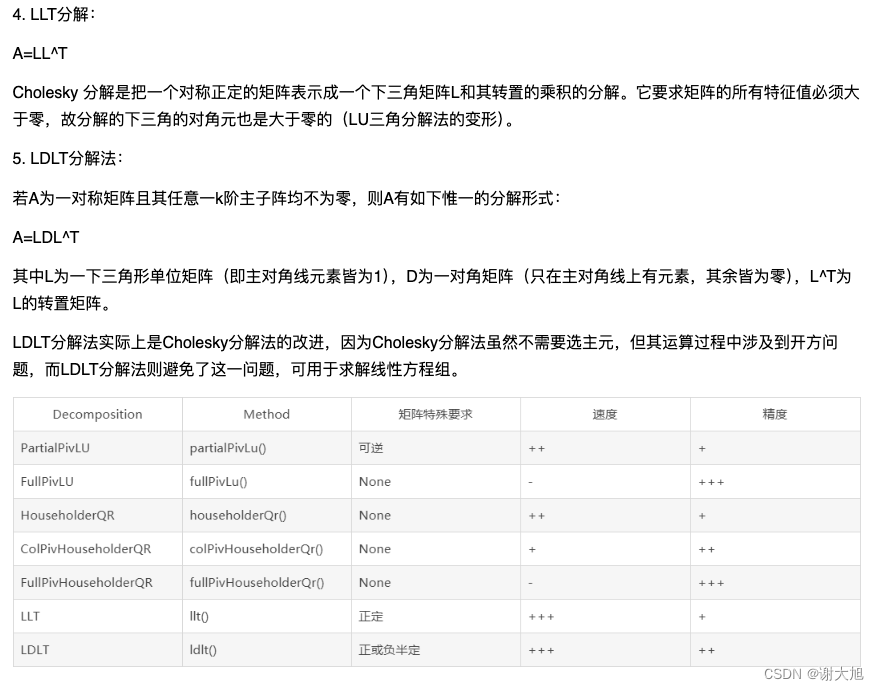
Eigen求解线性方程组
1、线性方程组的应用 线性方程组可以用来解决各种涉及线性关系的问题。以下是一些通常可以用线性方程组来解决的问题: 在实际工程和科学计算中,求解多项式方程的根有着广泛的应用。 在控制系统的设计中,我们经常需要求解特征方程的根来分析…...

7、Java基本数据类型的使用细节探讨(超详细版本)
Java基本数据类型的使用细节探讨 一、整数类型二、浮点数三、字符型四、布尔型 我觉得基本数据类型大家学计算机的应该都懂,但是韩顺平老师讲的基本类型的使用细节我觉得有必要记录一下,重新学的时候才发现有了新的感悟! 一、整数类型 使用细…...
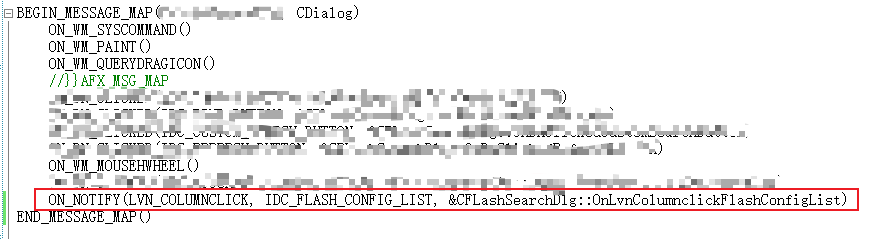
MFC实现点击列表头进行排序
MFC实现点击列表头排序 1、添加消息处理函数 在列表窗口右键,类向导。选择 IDC_LIST1(我的列表控件的ID),消息选择LVN_COLUMNCLICK。 2、消息映射如下 然后会在 cpp 文件中生成以下函数 void CFLashSearchDlg::OnLvnColumnclic…...
用龙梦迷你电脑福珑2.0做web服务器
用龙梦迷你电脑福珑2.0上做web服务器是可行的。已将一个网站源码放到该电脑,在局域网里可以访问网站网页。另外通过在同一局域网内的一台windows10电脑上安装花生壳软件,也可以在外网访问该内网服务器网站网页。该电脑的操作系统属于LAMP。在该电脑上安装…...

秋招后端开发面试题 - JVM类加载机制
目录 JVM类加载机制前言面试题能说一下类的生命周期吗?类加载的过程知道吗?类加载器有哪些?什么是双亲委派机制?为什么要用双亲委派机制?如何破坏双亲委派机制?如何判断一个类是无用的类? JVM类…...

OceanBase 分布式数据库【信创/国产化】- OceanBase 配置项和系统变量概述
本心、输入输出、结果 文章目录 OceanBase 分布式数据库【信创/国产化】- OceanBase 配置项和系统变量概述前言OceanBase 数据更新架构OceanBase 配置项和系统变量概述配置项配置项分类配置项查询系统变量系统变量分类系统变量查询配置项与系统变量的区分OceanBase 分布式数据库…...

单单单单单の刁队列
在数据结构的学习中,队列是一种常用的线性数据结构,它遵循先进先出(FIFO)的原则。而单调队列是队列的一种变体,它在特定条件下保证了队列中的元素具有某种单调性质,例如单调递增或单调递减。单调队列在处理…...
电脑windows系统压缩解压软件-Bandizip
一、软件功能 Bandizip是一款功能强大的压缩和解压缩软件,具有快速拖放、高速压缩、多核心支持以及广泛的文件格式支持等特点。 Bandizip软件的功能主要包括: 1. 支持多种文件格式 Bandizip可以处理多种压缩文件格式,包括ZIP, 7Z, RAR, A…...
图片公式识别@文档公式识别@表格识别@在线和离线OCR工具
文章目录 abstract普通文字识别本地软件识别公式扩展插件下载小结 在线识别网站/API👺Quicker整合(推荐)可视化编辑和识别公式其他多模态大模型识别图片中的公式排版 开源模型 abstract 本文介绍免费图片文本识别(OCR)工具,包括普通文字识别,公式识别,甚至是手写公…...
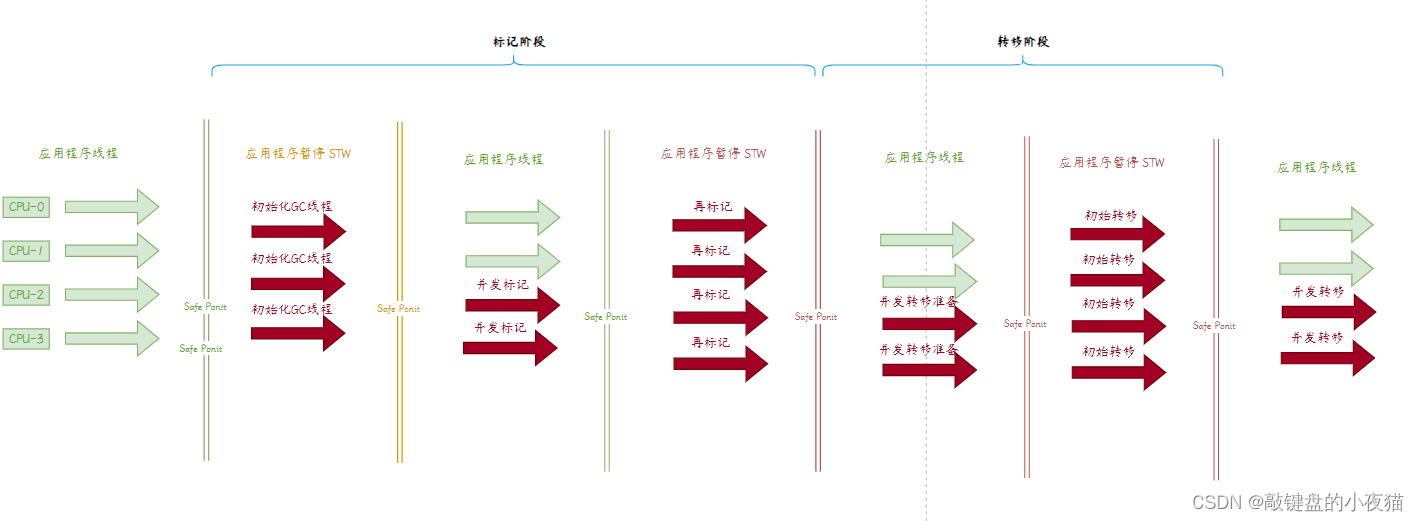
Java高阶私房菜:JVM分代收集算法介绍和各垃圾收集器原理分解
目录 什么是分代收集算法 GC的分类和专业术语 什么是垃圾收集器 垃圾收集器的分类及组合 编辑 应关注的核心指标 Serial和ParNew收集器原理 Serial收集器 ParNew收集器 Parallel和CMS收集器原理 Parallel 收集器 CMS收集器 新一代垃圾收集器G1和ZGC G1垃圾收集器…...

为什么IB损失要在100epochs后再用?
在给定的代码中,参数start_ib_epoch用于控制从第几轮开始使用IB(Instance-Balanced)损失函数进行训练。具体来说,如果start_ib_epoch的值大于等于100,那么在训练的前100轮中将使用普通的交叉熵损失函数(CE&…...
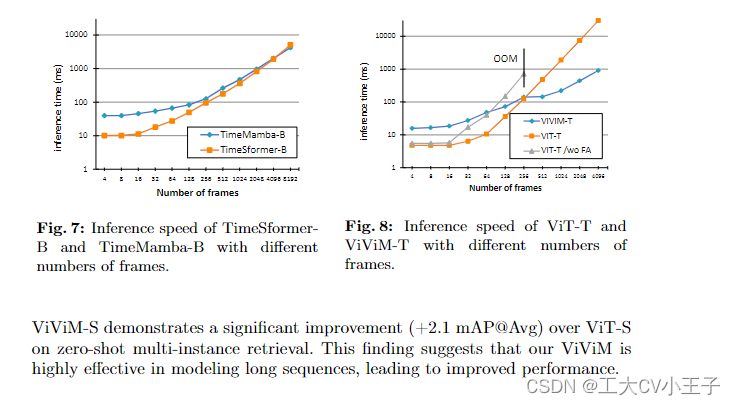
《Video Mamba Suite》论文笔记(4)Mamba在时空建模中的作用
原文翻译 4.4 Mamba for Spatial-Temporal Modeling Tasks and datasets.最后,我们评估了 Mamba 的时空建模能力。与之前的小节类似,我们在 Epic-Kitchens-100 数据集 [13] 上评估模型在zero-shot多实例检索中的性能。 Baseline and competitor.ViViT…...
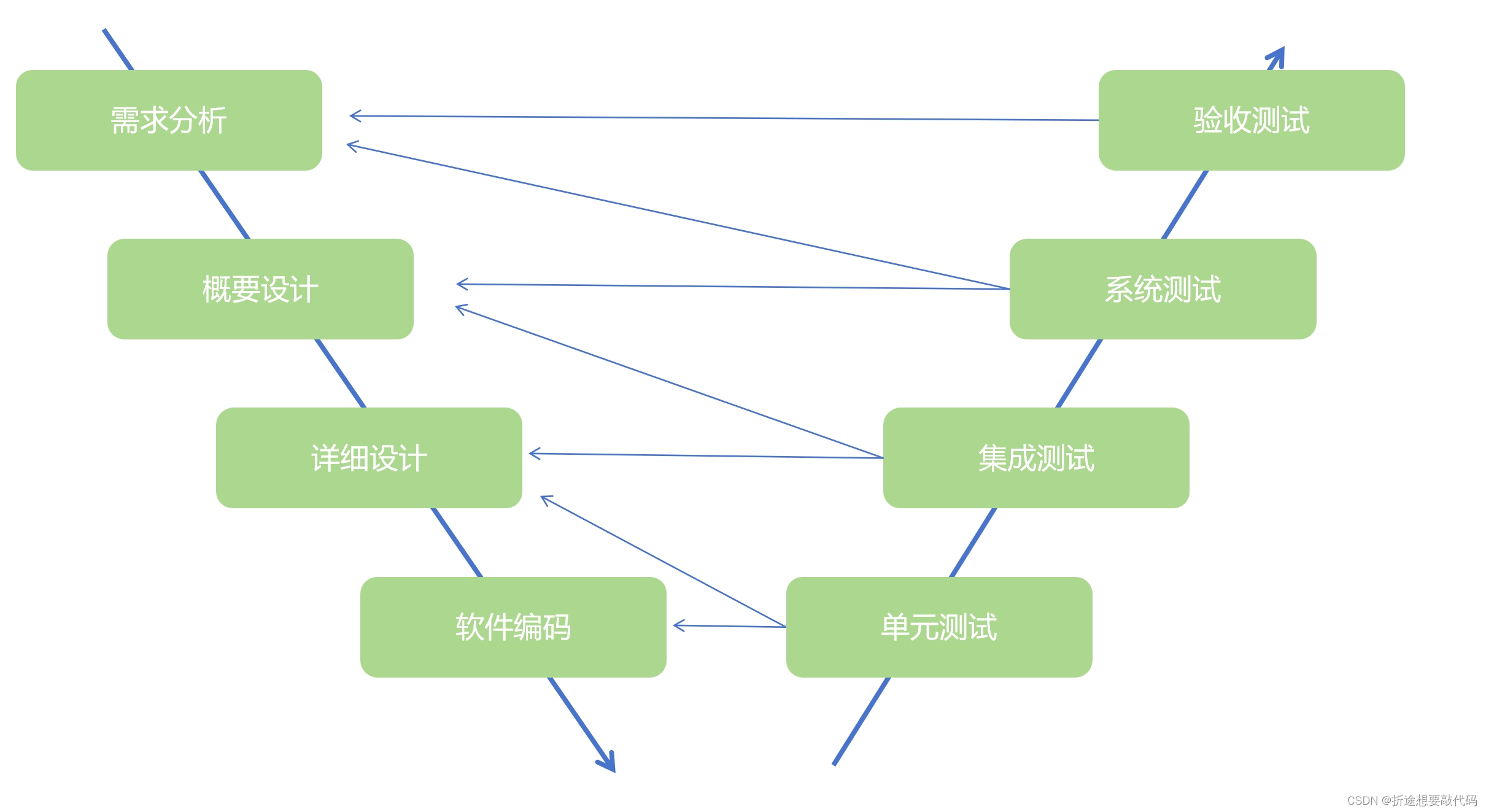
【备战软考(嵌入式系统设计师)】10 - 软件工程基础
这一部分的内容是概念比较多,不要理解,去感受。 涉及的知识点是嵌入式系统开发和维护的部分,也就是和管理相关的,而不是具体如何进行嵌入式系统开发的细节。 系统开发生命周期 按照顺序有下面几个阶段,我们主要要记…...

随手笔记-GNN(朴素图神经网络)
自己看代码随手写的一点备忘录,自己看的,不喜勿喷 GNN (《------ 代码) 刚开始我还在怀疑为什么没有加weigth bias,已经为什么权重才两个,原来是对node_feats进行的network的传播,而且自己内部直接进行了。 下面是一…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...
