Java 7大排序
🐵本篇文章将对数据结构中7大排序的知识进行讲解

一、插入排序
有一组待排序的数据array,以升序为例,从第二个数据开始(用tmp表示)依次遍历整组数据,每遍历到一个数据都再从tmp的前一个数据开始(下标用j表示)从后往前依次和其进行比较,如果tmp比它小,则令array[j + 1] = array[j];
1.1 实例讲解
第一趟:

第二趟:

第三趟和第四躺:
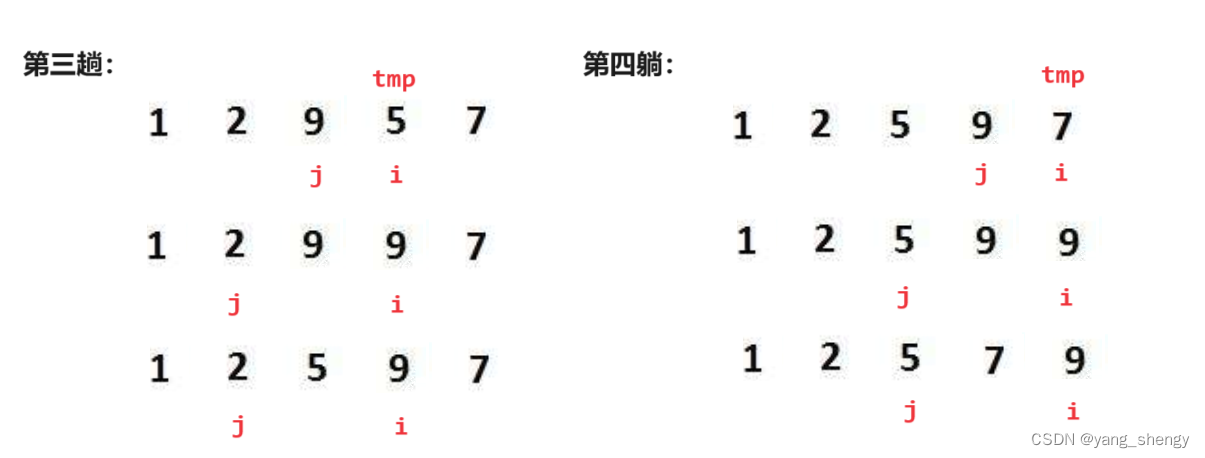
1.2 代码实现
public void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i - 1;for (; j >= 0; j--) {if (tmp < array[j]) {array[j + 1] = array[j]; //将tmp移动到当前数据顺序的最小位置处,此步操作相当于给tmp腾位置} else {break;}}array[j + 1] = tmp;}}
在该排序算法中,当tmp前面出现比其小的元素时,则再往前的数据也一定比tmp小,所以插入排序是元素越有序,其效率越快的排序算法
时间复杂度:O(N²)
空间复杂度:O(1)
稳定
二、希尔排序
希尔排序是对直接插入排序的优化,它会将一组数据进行分组,然后针对每一组进行直接插入排序,那么该如何进行分组:定义一个gap,代表同一组数据的间隔,比如由一组数据:6,5,4,3,2,1;gap = 2,则6,4,2为一组,5,3,1为一组。在gap = 2的情况下的每一组数据排序完毕后,要缩小gap并再进行分组,然后再对每一组进行插入排序,随着gap的减小,该组数据会变得越来越有序,当gap = 1时,此时数据已经接近有序了,所以效率会非常快
2.1 实例讲解
第一躺:
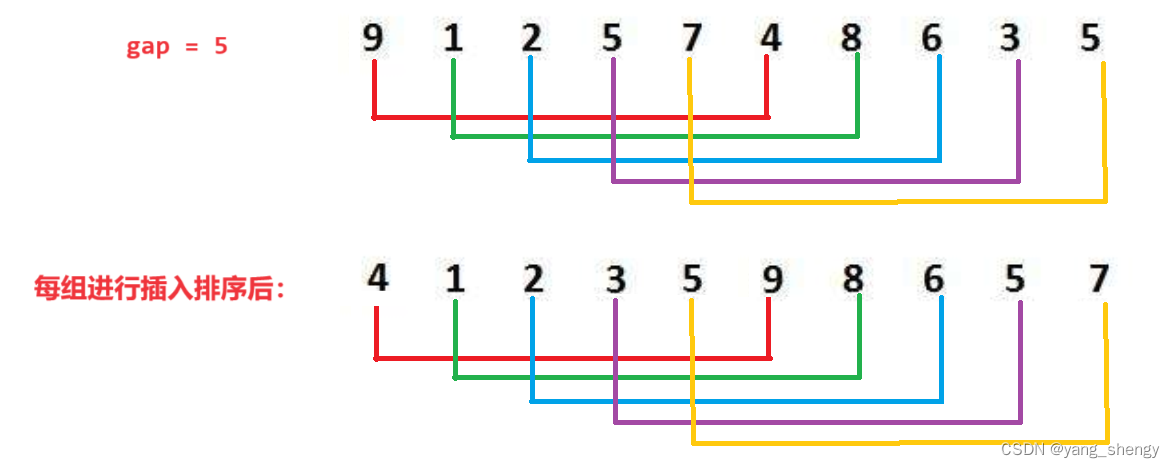
第二趟:
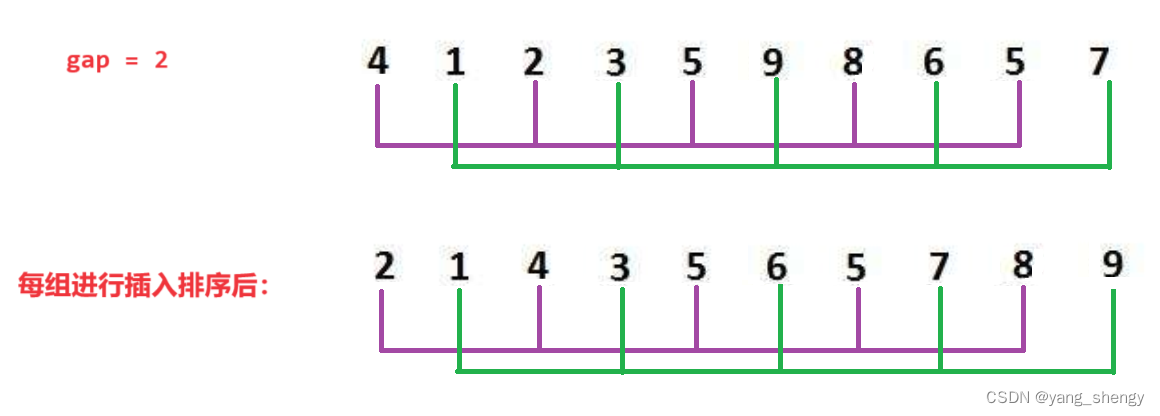
第三趟:

2.2 代码实现
public void shellSort(int[] array) {int gap = array.length;while(gap > 1) { //当gap = 1时分组结束gap = gap / 2;shell(array, gap);}}private void shell(int[] array, int gap) {for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i - gap;for (; j >= 0; j -= gap) {if (tmp < array[j]) {array[j + gap] = array[j];} else {break;}}array[j + gap] = tmp;}}
希尔排序不稳定
三、选择排序
选择排序较为简单,这里直接讲实例
3.1 实例讲解
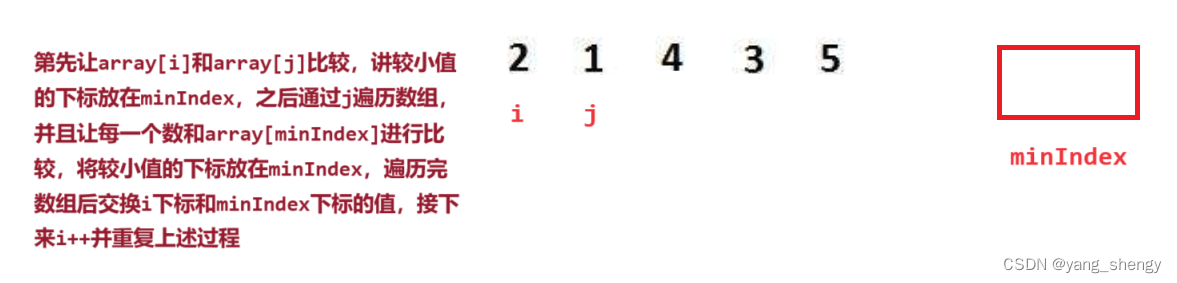
第一躺:

第二趟:

第三趟:

第四躺和第五躺也都是如此排序的,由于数据已经有序,这里就不再演示
3.2 代码实现
public void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;int j = i + 1;for (; j < array.length; j++) {if (array[j] < array[minIndex]) {minIndex = j;}}swap(array, minIndex, i);}}private void swap(int[] array, int minIndex, int i) {int tmp = array[minIndex];array[minIndex] = array[i];array[i] = array[minIndex];}
选择排序的效率不是很高,日常开发使用较少
时间复杂度:O(N²)
空间复杂度:O(1)
不稳定
四、堆排序
在上篇文章:Java优先级队列(堆)中进行了讲解,这里只给出代码:
4.1 代码实现
public void createHeap(int[] array) { //创建大根堆int usedSize = array.length;for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {siftDown(array, parent, usedSize);}}private void siftDown(int[] array, int parent, int end) { //向下调整int child = 2 * parent + 1;while(child < end) {if (child + 1 < end && array[child] < array[child + 1]) {child++;}if (array[parent] < array[child]) {swap(array, parent, child);parent = child;child = 2 * parent + 1;} else {break;}}}private void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}public void heapSort(int[] array) { //堆排序createHeap(array);int end = array.length - 1;while(end > 0) {swap(array, 0, end);siftDown(array, 0, end - 1);end--;}}堆排序:
时间复杂度:O(N * logN)
空间复杂度:O(1)
不稳定
五、冒泡排序
冒泡排序在C语言阶段也进行了详细讲解,这里也只给出代码:
5.1 代码实现
public void bubbleSort(int[] array) {for (int i = array.length - 1; i > 0; i--) {for (int j = 0; j < i; j++) {if (array[j] > array[j + 1]) {int tmp = array[j];array[j] = array[j + 1];array[j + 1] = tmp;}}}}
冒泡排序
时间复杂度:O(N²)
空间复杂度:O(1)
稳定
六、快速排序
6.1 实例讲解
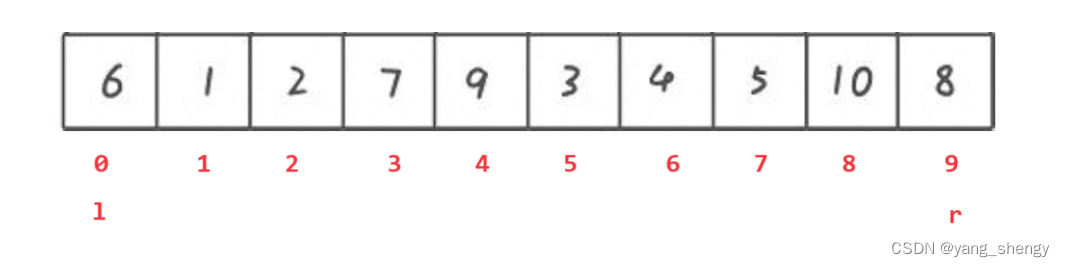
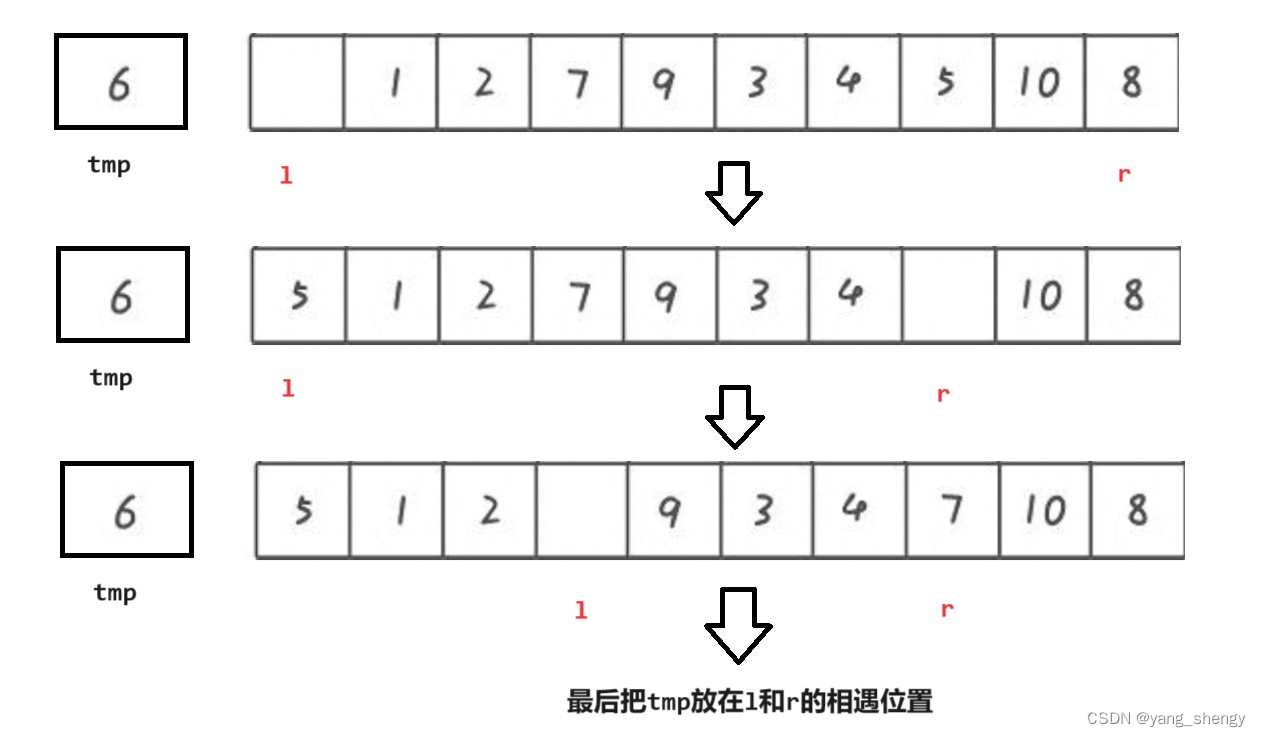
以最左边的数作为基准,先从数组的最右边开始遍历,当找到比基准小的数时停止,然后从数组的最左边开始遍历,当找到比基准大的数时停止,这时将 l 和 r 所对应的值进行交换,之后重复上述过程直到 left 和 right 相遇,相遇的下标定义为pivot,最后将pivot下标的值和tmp进行交换
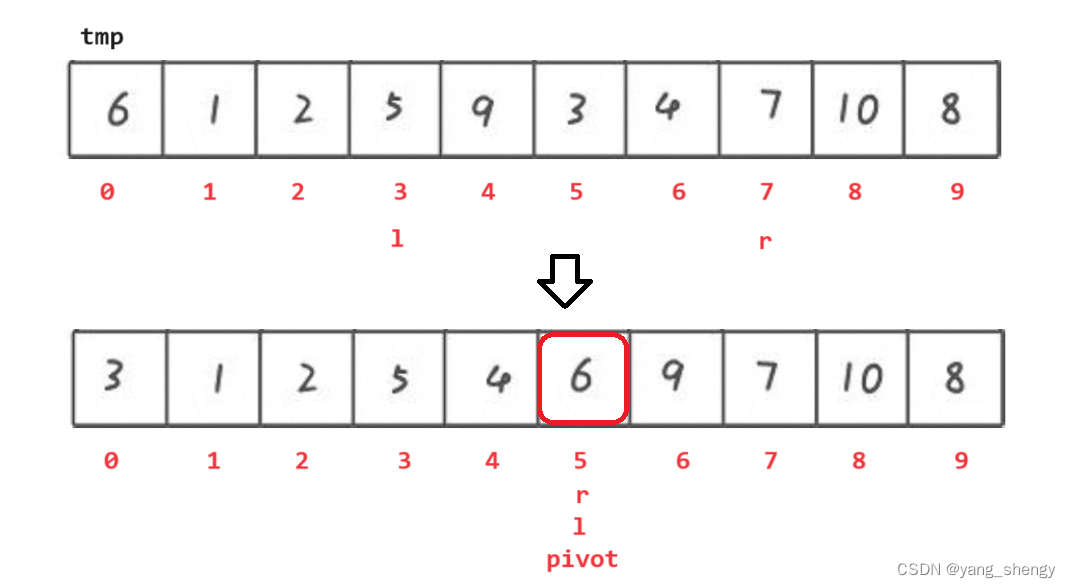
此时6的左边都是比其小的数,6的右边都是比其大的数;之后分别对6左边的数据和右边的数据进行重复的操作
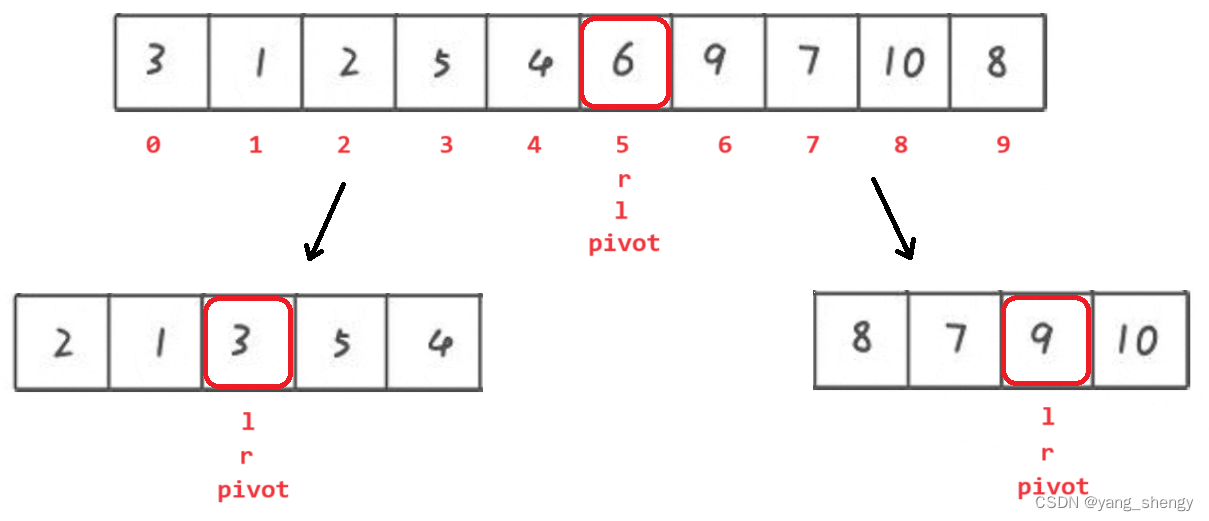
之后再对这两组数据的pivot的两边进行重复操作,由此可以联想到使用递归,类似于二叉树
6.2 代码实现
public void quickSort(int[] array) {quick(array, 0, array.length - 1);}private void quick(int[] array, int start, int end) {int pivot = partition(array, start, end); //通过paratition方法得到 left 和 right 相遇的下标 (paratition后续再实现)quick(array, start, pivot - 1); //递归 pivot 的左边quick(array, pivot + 1, end); //递归 pivot 的右边}上述的 quick 方法中还缺少递归结束的条件,第一种不难想到就是left 和 right相遇时
第二种情况如下图:
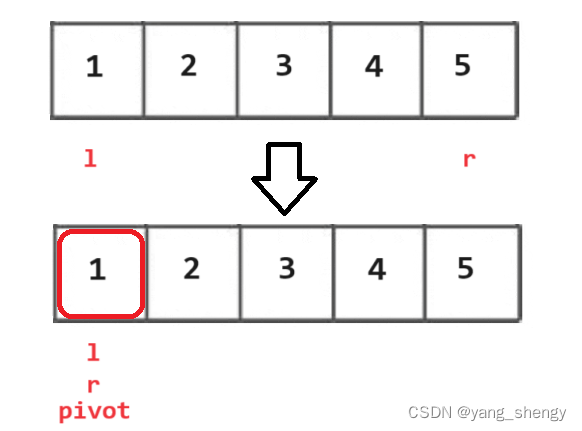
上图的下一步是r = pivot - 1;开始递归pivot的左边,但其左边并没有数据,所以当left > right时结束递归
public void quickSort(int[] array) {quick(array, 0, array.length - 1);}private void quick(int[] array, int start, int end) {if (start >= end) {return;}int pivot = partition1(array, start, end);quick(array, start, pivot - 1);quick(array, pivot + 1, end);}private int partition(int[] array, int left, int right) { //确定pivotint tmp = array[left]; //基准int i = left;while(left < right) {while(left < right && array[right] >= tmp) {right--;}while(left < right && array[left] <= tmp) {left++;}swap(array, left, right);}swap(array, i, right);return left;}上述的 partition 确定pivot的下标被称为Hoare法,接下来再介绍一种 “挖坑法”

仍然是先从右边开始遍历,找到比tmp小的数则放在空出来的位置,此时right下标的位置就空出来了,然后从左边开始遍历找到比tmp大的数则放在空出来的位置,重复上述过程
// 挖坑法private int partition(int[] array, int left, int right) {int tmp = array[left];while(left < right) {while(left < right && array[right] >= tmp) {right--;}array[left] = array[right];while(left < right && array[left] <= tmp) {left++;}array[right] = array[left];}array[left] = tmp;return left;}
6.3 快速排序的优化
一组数据在较为理想的情况下,每次找到的基准元素都可以将这组数据分为大致相等的两部分,此时的快速排序算法的时间复杂度为 O(nlogn) ,但是也会存在一些极端的情况:每次找到的基准元素都是这组数据的最大值或最小值,此时会出现"单分支"的情况,时间复杂度为O(n^2)

6.3.1 三数取中法
改优化方法主要针对趋于有序的待排数组(升序或逆序),比如有这样一组数据:1,2,3,4,5在每一次取基准元素之前,分别取该数组的第一个数,最后一个数和中间的数,取这三个数的中间大的数和第一个数进行交换,交换完后上述数组就会变成:3,2,1,4,5,这样就是上述提到的较为理想的情况
private static void quick(int[] array, int start, int end) {if (start >= end) {return;}//如果待排数组趋于有序,则采用三数取中法进行优化int index = middleNum(array, start, end);swap (array, start, index);int pivot = partition(array, start, end);quick (array, start, pivot - 1);quick (array, pivot + 1, end);}
6.3.2 递归到小的子区间时,进行直接插入排序
之前有说道:待排数据的有序性越强,直接插入排序的效率越高,所以可以考虑当快排的递归深度较深或者说递归到的子区间较小时,采用直接插入排序,这样也可以提升快速排序的效率
private static void quick(int[] array, int start, int end) {if (start >= end) {return;}//如果区间较小,则使用这种优化if (end - start + 1 <= 10) {insertSort(array, start, end);return;}int pivot = partition(array, start, end);quick (array, start, pivot - 1);quick (array, pivot + 1, end);}public static void insertSort(int[] array, int start, int end) { //这里不能只传数组,因为并不是对整个数组进行插入排序,而是某一个子区间进行直接插入排序for (int i = start + 1; i <= end; i++) { //由于只是对特定的区间进行插入排序,所以这里要限定空间int tmp = array[i];int j = i - 1;for (; j >= start; j--) { // >=startif (array[j] > tmp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = tmp;}}
快速排序时间复杂度:最好:O(N*logN),最坏:O(N²),平均:O(N*logN)
空间复杂度:O(logN)
不稳定
七、归并排序
7.1 实例讲解
归并排序是先将待排数组递归的进行两两分组,直到每组只有一个元素,之后两两递归的进行有序合并
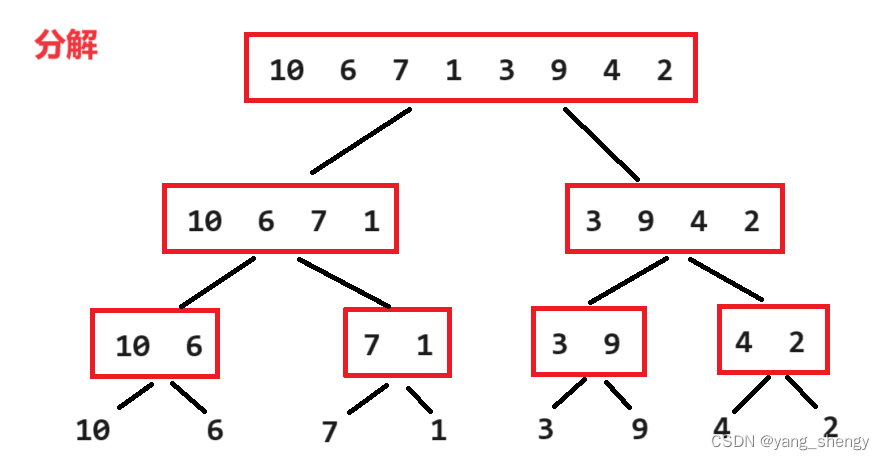
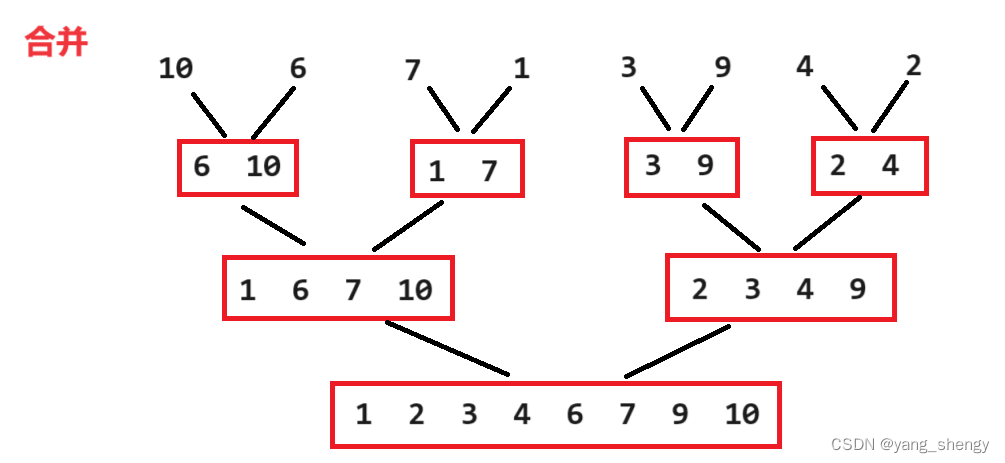
7.2 代码实现
先进行分解
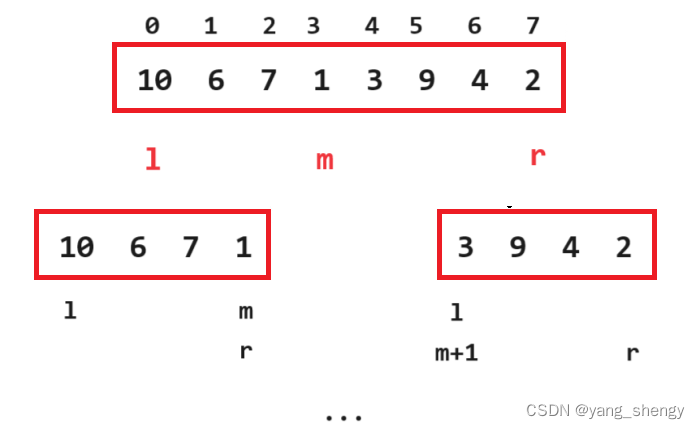
public static void mergeSort (int[] array) {//将待排数组进行分解mergeFunc(array, 0, array.length - 1);}private static void mergeFunc (int[] array, int left, int right) {if (left >= right) {return;}int mid = left + ((right - left) >> 1); //得到改组数据的中间下标//分别分解数组的左边和右边mergeFunc (array, left, mid);mergeFunc (array, mid + 1, right);//将分解后的数组进行 二路归并merge (array, left, mid, right);}
之后进行合并,以下面这一组为例:

将上面这两组数据进行有序合并,可以给这两组数据的第一个元素和最后一个元素的下标分别定义为s1,e1,s2,e2;之后再创建一个数组tmpArr,每次比较s1和s2的值,并将较小的值放在tmpArr中,(如果s1的值较小则s1++,反之s2++),然后将tmpArr中的数据再拷贝到原数组中
private static void merge (int[] array, int left, int mid, int right) {int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;int[] tmpArr = new int[right - left + 1];int k = 0;//1.保证两个表都有数据while (s1 <= e1 && s2 <= e2) {if (array[s1] < array[s2]) {tmpArr[k++] = array[s1++];} else {tmpArr[k++] = array[s2++];}}//2.上个循环走完之后,可能还有一个表的数据没有全部放到tmpArr中while (s1 <= e1) {tmpArr[k++] = array[s1++];}while (s2 <= e2) {tmpArr[k++] = array[s2++];}//3.将tmpArr中的数据拷贝回原数组中for (int i = 0; i < k; i++) {array[i + left] = tmpArr[i]; //array[i + left]是因为合并的两组数据不一定是原数组的0下标开始}}
时间复杂度:O(N*logN)
空间复杂度:O(N)
不稳定
🙉本篇文章到此结束
相关文章:

Java 7大排序
🐵本篇文章将对数据结构中7大排序的知识进行讲解 一、插入排序 有一组待排序的数据array,以升序为例,从第二个数据开始(用tmp表示)依次遍历整组数据,每遍历到一个数据都再从tmp的前一个数据开始࿰…...

vue3 - 图灵
目录 vue3简介整体上认识vue3项目创建Vue3工程使用官方脚手架创建Vue工程[推荐] 主要⼯程结构 数据双向绑定vue2语法的双向绑定简单表单双向绑定复杂表单双向绑定 CompositionAPI替代OptionsAPICompositionAPI简单不带双向绑定写法CompositionAPI简单带双向绑定写法setup简写⽅…...

java设计模式八 享元
享元模式(Flyweight Pattern)是一种结构型设计模式,它通过共享技术有效地支持大量细粒度的对象。这种模式通过存储对象的外部状态在外部,而将不经常变化的内部状态(称为享元)存储在内部,以此来减…...

ELK原理详解
ELK原理详解 一、引言 在当今日益增长的数据量和复杂的系统环境中,日志数据的收集、存储、分析和可视化成为了企业运营和决策不可或缺的一部分。ELK(Elasticsearch、Logstash、Kibana)堆栈凭借其高效的性能、灵活的扩展性和强大的功能&…...
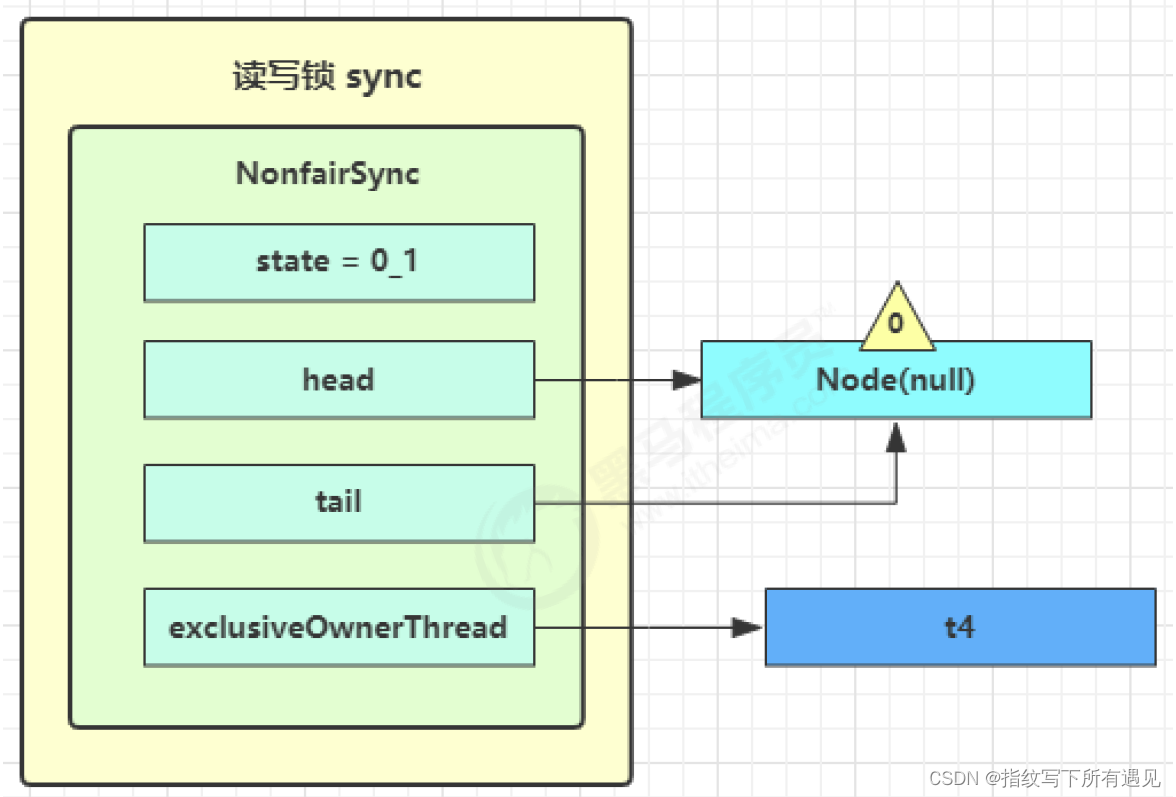
多线程学习Day09
10.Tomcat线程池 LimitLatch 用来限流,可以控制最大连接个数,类似 J.U.C 中的 Semaphore 后面再讲 Acceptor 只负责【接收新的 socket 连接】 Poller 只负责监听 socket channel 是否有【可读的 I/O 事件】 一旦可读,封装一个任务对象&#x…...

第33次CSP认证Q1:词频统计
🍄题目描述 在学习了文本处理后,小 P 对英语书中的 𝑛n 篇文章进行了初步整理。 具体来说,小 P 将所有的英文单词都转化为了整数编号。假设这 𝑛n 篇文章中共出现了 𝑚m 个不同的单词,则把它们…...
pytorch加载模型出现错误
大概的错误长下面这样: 问题出现的原因: 很明显,我就是犯了第一种错误。 网上的修改方法: 我觉得按道理哈,确实,蓝色部分应该是可以把问题解决了的。但是我没有解决,因为我犯了另外一个错…...
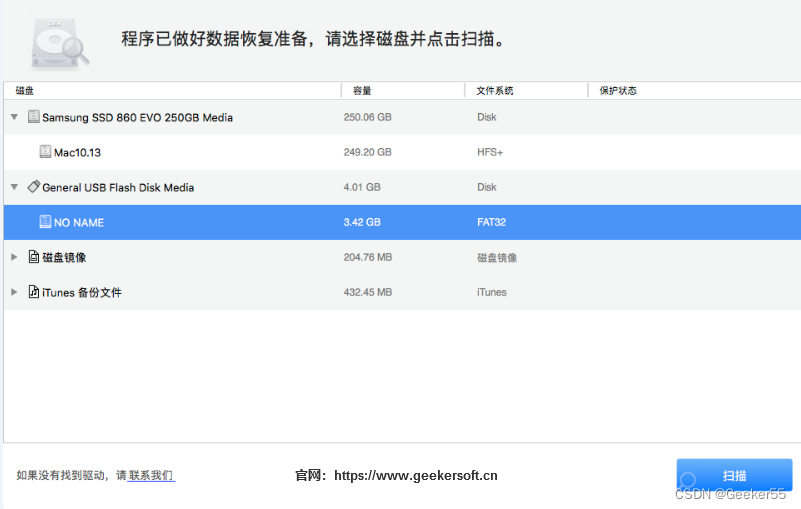
如何在Mac上恢复格式化硬盘的数据?
“嗨,我格式化了我的一个Mac硬盘,而没有使用Time Machine备份数据。这个硬盘被未知病毒感染了,所以我把它格式化为出厂设置。但是,我忘了备份我的文件。现在,我想恢复格式化的硬盘驱动器并恢复我的文档,您能…...

华为OD机试 - 手机App防沉迷系统(Java 2024 C卷 100分)
华为OD机试 2024C卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试(JAVA)真题(A卷B卷C卷)》。 刷的越多,抽中的概率越大,每一题都有详细的答题思路、详细的代码注释、样例测试…...
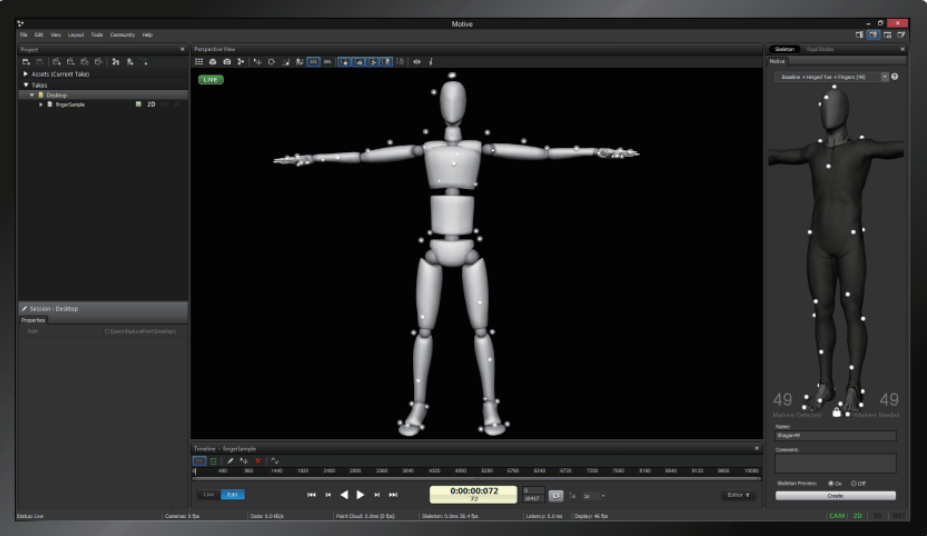
搜维尔科技:光学动作捕捉系统用于城市公共安全智慧感知实验室
用户名称:西安科技大学 主要产品:Optitrack Priime41 光学动作捕捉系统(8头) 在6米8米的空间内,通过8个Optitrack Priime41光学动作捕捉镜头,对人体动作进行捕捉,得到用户想要的人体三维空间坐…...
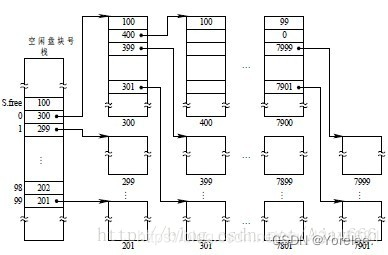
保研面试408复习 4——操作系统、计网
文章目录 1、操作系统一、文件系统中文件是如何组织的?二、文件的整体概述三、UNIX外存空闲空间管理 2、计算机网络一、CSMA/CD 协议(数据链路层协议)二、以太网MAC帧MTU 标记文字记忆,加粗文字注意,普通文字理解。 1、…...

实战攻防中关于文档的妙用
一、PPT钓鱼 简单制作一个用于钓鱼的PPTX文件 一般那种小白不知道PPT也能拿来钓鱼,这里主要是借用PPT中的”动作按钮”, 我们在插入的地方,选择“动作按钮” 然后在弹出的窗口处: 比如填入上线CS的语句:powershell.exe -nop -w …...

【使用ChatGPT的API之前】OpenAI API提供的可用模型
文章目录 一. ChatGPT基本概念二. OpenAI API提供的可用模型1. InstructGPT2. ChatGPT3. GPT-4 三. 在OpenAI Playground中使用GPT模型-ing 在使用GPT-4和ChatGPT的API集成到Python应用程序之前,我们先了解ChatGPT的基本概念,与OpenAI API提供的可用模型…...

【C语言】模拟实现深入了解:字符串函数
🔥引言 本篇将模拟实现字符串函数,通过底层了解更多相关细节 🌈个人主页:是店小二呀 🌈C语言笔记专栏:C语言笔记 🌈C笔记专栏: C笔记 🌈喜欢的诗句:无人扶我青云志 我自…...

钩子函数onMounted定义了太多访问MySQL的操作 导致数据库异常
先放几种后端遇到的异常,多数和数据库有关 pymysql.err.InternalError: Packet sequence number wrong - got 102 expected 1 127.0.0.1 - - [09/May/2024 17:49:37] "GET /monitorLastTenList HTTP/1.1" 500 AttributeError: NoneType object has no at…...
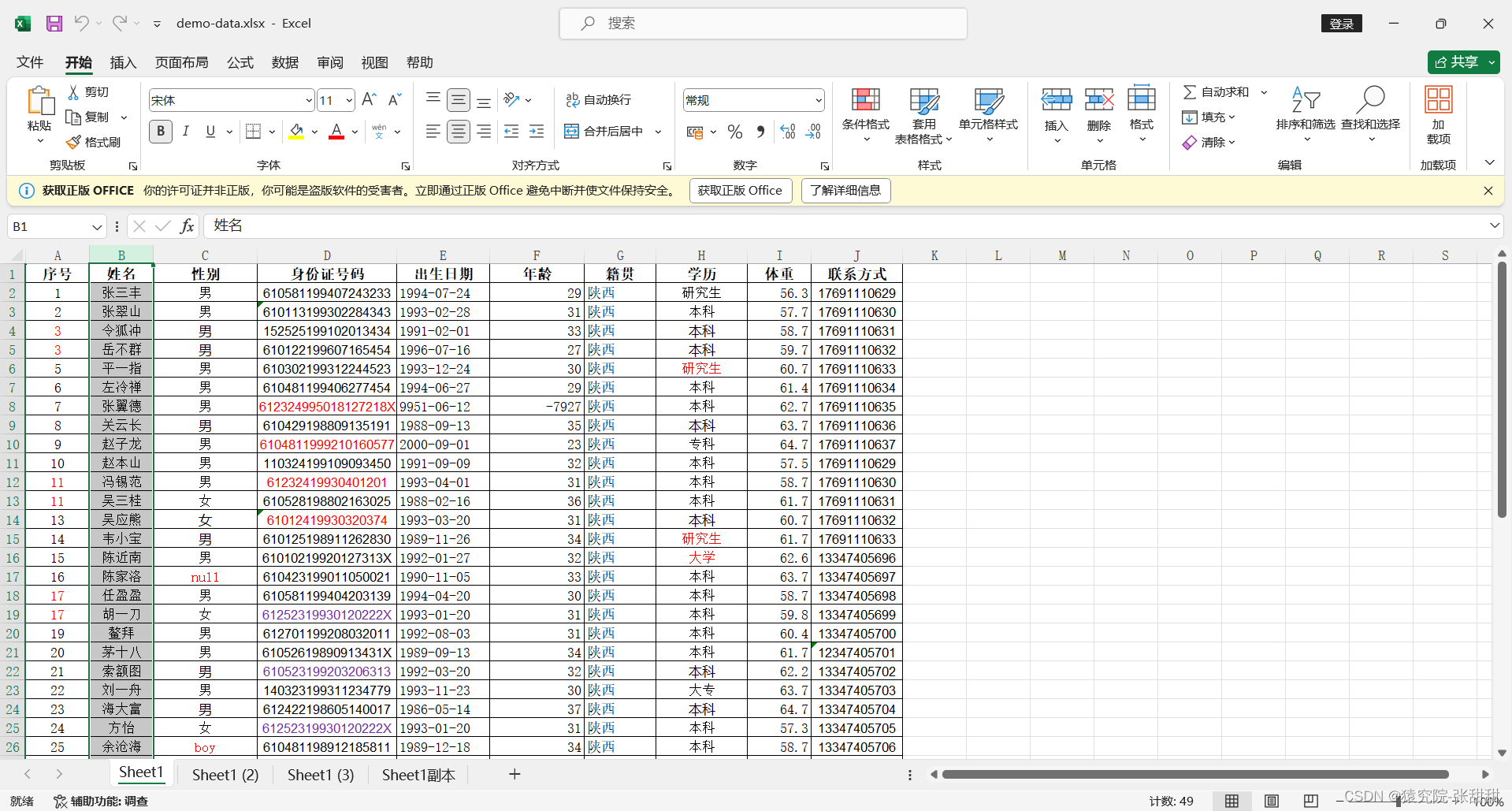
Excel文件解析---超大Excel文件读写
1.使用POI写入 当我们想在Excel文件中写入100w条数据时,使用XSSFWorkbook进行写入时会发现,只有将100w条数据全部加载到内存后才会用write()方法统一写入,效率很低,所以我们引入了SXXFWorkbook进行超大Excel文件读写。 通过设置 …...

TypeScript基础:类型系统介绍
TypeScript基础:类型系统介绍 引言 TypeScript,作为JavaScript的一个超集,引入了类型系统,这为开发大型应用程序带来了诸多好处。本文将介绍TypeScript类型系统的基础知识,帮助初学者理解其概念和用法。 基础知识 …...
【Unity】Unity项目转抖音小游戏(一) 项目转换
UnityWEBGL转抖音小游戏流程 业务需求,开始接触一下抖音小游戏相关的内容,开发过程中记录一下流程。 相关参考: 抖音文档:https://developer.open-douyin.com/docs/resource/zh-CN/mini-game/develop/guide/game-engine/rd-to-SC…...

element-ui 中修改loading加载样式
element-ui 中的 loading 加载功能,默认是全屏加载效果 设置局部,需要自定义样式或者修改样式,方法如下: import { Loading } from element-uiVue.prototype.$baseLoading (text) > {let loadingloading Loading.service({…...
)
QT登录界面,(页面的切换)
以登陆界面为例,(QDialog) 1.主界面先构造login 的对话框类 int main(int argc, char *argv[]) {QApplication a(argc, argv);//先显示Login的界面Study_Login_Dialog login;............ }2.Login的类,可以用自定义的信号&#…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
