704. 二分查找
Problem: 704. 二分查找
🐷我的leetcode主页
文章目录
- 题目
- 分类
- 思路
- 什么是二分查找
- 如何理解时间复杂度
- 解题方法
- Code
题目
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
-
你可以假设 nums 中的所有元素是不重复的。
-
n 将在 [1, 10000]之间。
-
nums 的每个元素都将在 [-9999, 9999]之间。
分类
二分查找
思路
什么是二分查找
二分查找是一种查找算法,它的基本思想是:通过比较元素的大小来缩小查找范围,直到找到目标元素或查找范围为空。
场景样例:
-
假设要在电话簿中找一个名字以 K 打头的人,(现在谁还用电话簿!)可以从头开始翻页,直到进入以 K 打头的部分。但你很可能不这样做,而是从中间开始,因为你知道以 K 打头的名字在电话簿中间。所以你会直接从中间开始找。
-
两个人玩游戏,A想一个1-100的数字(比如是60),B来猜。
如果B从1开始猜,一直猜到99才能猜到,那么时间复杂度是O(n)
如果B从50开始猜,A会告诉B猜小了,那么B肯定会在50-100里面猜,那么就排除了一半1-50的数字
B再从75开始猜,A会告诉B猜大了,下次一B肯定在50-75里面猜,又排除了一半75-100的数字
这样依次类推,最终最多猜测O(logn)次,就能猜到最终共的答案。
如何理解时间复杂度
大 O 表示法指出了最糟情况下的运行时间
比如上面的例子,1-100采用线性放大依次猜,猜到100才能猜对的话,那么就需要猜测n次,所以复杂度是O(n);
如果采用二分查找,那么最多需要猜测100对2取对数的次数,那么时间复杂度是O(logn)。
通俗理解的话可以理解为操作数
比如要在一张正方形的纸上面画16个格子,那么最坏情况下,一个一个画,需要画16次,所以时间复杂度是O(n)。
如果采用折叠的方式,对折一次,产生2个格子,两次产生4个格子,3次产生8个格子,4次产生16个格子,那么时间复杂度是O(logn)。
解题方法
Code
def search(self, nums, target):""":type nums: List[int]:type target: int:rtype: int"""low = 0high = len(nums) - 1while low <= high:mid = (low + high) // 2if nums[mid] == target:return midelif nums[mid] < target:low = mid + 1else:high = mid - 1return -1
相关文章:

704. 二分查找
Problem: 704. 二分查找 🐷我的leetcode主页 文章目录 题目分类思路什么是二分查找如何理解时间复杂度 解题方法Code 题目 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target&a…...

php回车变br、php显示br
在 PHP 中,如果你想将回车符(\n)转换为 HTML 的 <br> 标签来实现换行显示,可以使用内置函数 nl2br()。这个函数会将文本中的换行符替换为 <br> 标签。以下是使用 nl2br() 函数的示例代码: <?php $tex…...
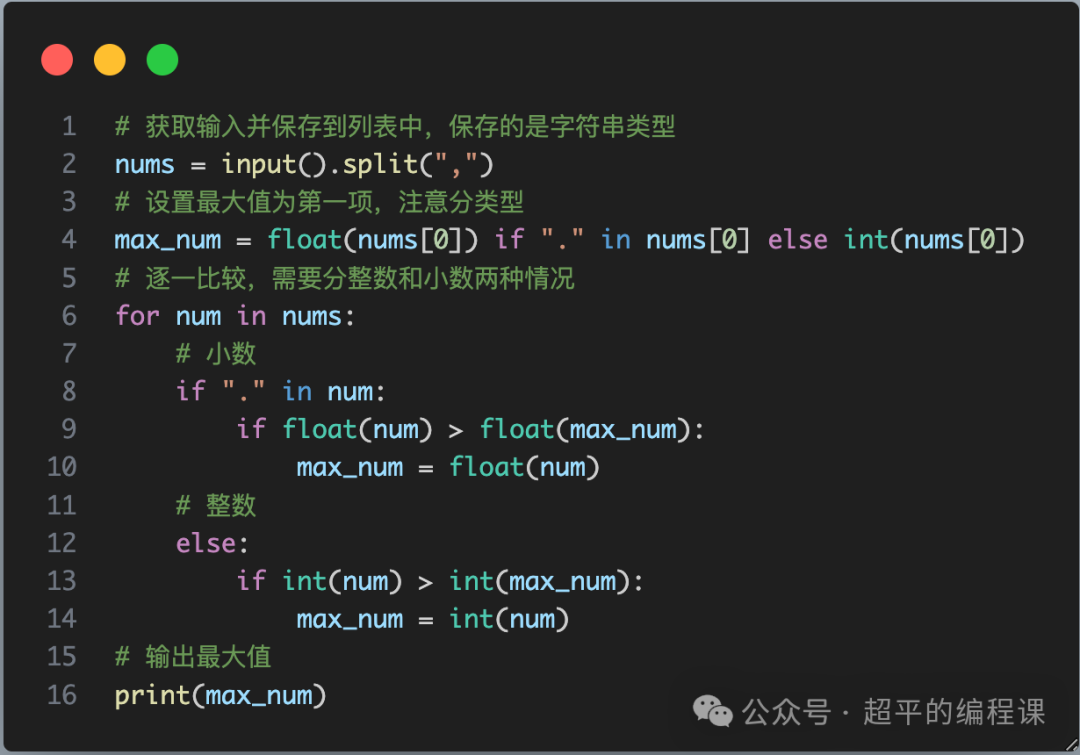
找最大数字-第12届蓝桥杯国赛Python真题解析
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第60讲。 找最大数字&#…...

蓝桥杯 算法提高 ADV-1170 阶乘测试 python AC
找规律题,遍历i中有几个m就加几,和m的多少次数有关 第一版👇 try:while True:n, m map(int, input().split())ll [i for i in range(1, n 1) if i % m 0]ans len(ll)M mwhile ll:lll []M * mfor i in ll:if i % M 0:lll.append(i)a…...

阿里巴巴杭州全球总部正式启用,创新“减碳大脑”科技减碳 | 最新快讯
来源:封面新闻 封面新闻记者付文超 5 月 10 日,记者获悉,位于未来科技城的阿里巴巴杭州全球总部新园区正式启用,这是阿里巴巴目前最大的综合性办公园区。从空中俯瞰,园区正中央呈现阿里标志性的笑脸 logo,这…...
)
蓝桥杯国赛练习题真题Java(矩阵计数)
题目描述 一个 NM 的方格矩阵,每一个方格中包含一个字符 O 或者字符 X。 要求矩阵中不存在连续一行 3 个 X 或者连续一列 3 个 X。 问这样的矩阵一共有多少种? 输入描述 输入一行包含两个整数 N,M (1≤N,M≤5)。 输出描述 输出一个整数代表答案。…...
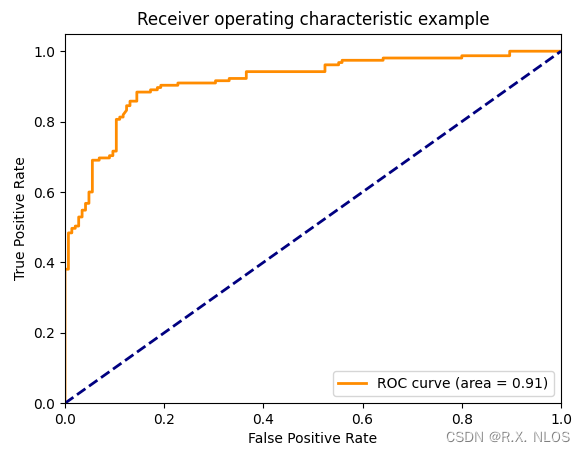
概念解析 | ROC曲线:评估分类模型
注1:本文系"概念解析"系列之一,致力于简洁清晰地解释、辨析复杂而专业的概念。本次辨析的概念是:ROC曲线的含义和绘制 概念解析 | ROC曲线:评估分类模型 第一部分:通俗解释 在我们的日常生活中,经常会遇到需要做出判断和选择的情况。比如,当你收到一封邮件时…...
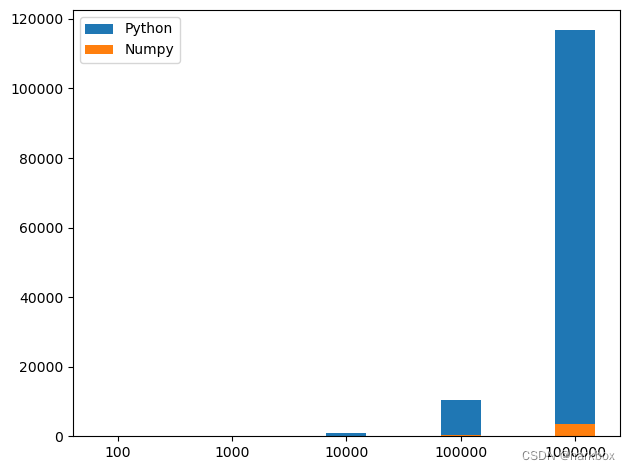
数据可视化训练第二天(对比Python与numpy中的ndarray的效率并且可视化表示)
绪论 千里之行始于足下;继续坚持 1.对比Python和numpy的性能 使用魔法指令%timeit进行对比 需求: 实现两个数组的加法数组 A 是 0 到 N-1 数字的平方数组 B 是 0 到 N-1 数字的立方 import numpy as np def numpy_sum(text_num):"""…...
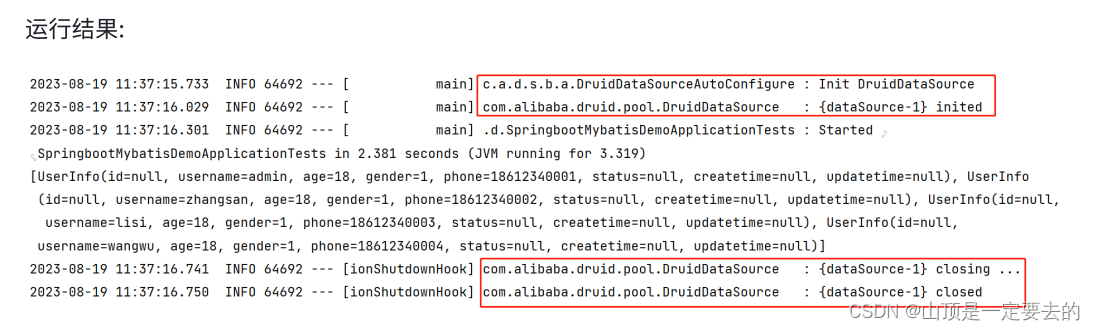
【Java EE】数据库连接池详解
文章目录 🎍数据库连接池🌸Hikari🌸Druid 🍀MySQL开发企业规范⭕总结 🎍数据库连接池 在上⾯Mybatis的讲解中,我们使⽤了数据库连接池技术,避免频繁的创建连接,销毁连接 下⾯我们来了解下数据库连接池 数据库连接池负…...

正点原子[第二期]Linux之ARM(MX6U)裸机篇学习笔记-15.4讲 GPIO中断实验-IRQ中断服务函数详解
前言: 本文是根据哔哩哔哩网站上“正点原子[第二期]Linux之ARM(MX6U)裸机篇”视频的学习笔记,在这里会记录下正点原子 I.MX6ULL 开发板的配套视频教程所作的实验和学习笔记内容。本文大量引用了正点原子教学视频和链接中的内容。…...

如何平衡RPA机器人的安全性与业务敏捷性,同时不牺牲用户体验?
平衡RPA机器人的安全性与业务敏捷性,同时不牺牲用户体验,是RPA实施中的一个关键挑战。以下是一些策略和最佳实践: ### 1. 安全设计原则 从设计阶段就将安全性纳入考虑,遵循安全设计原则。这意味着在开发RPA解决方案时࿰…...
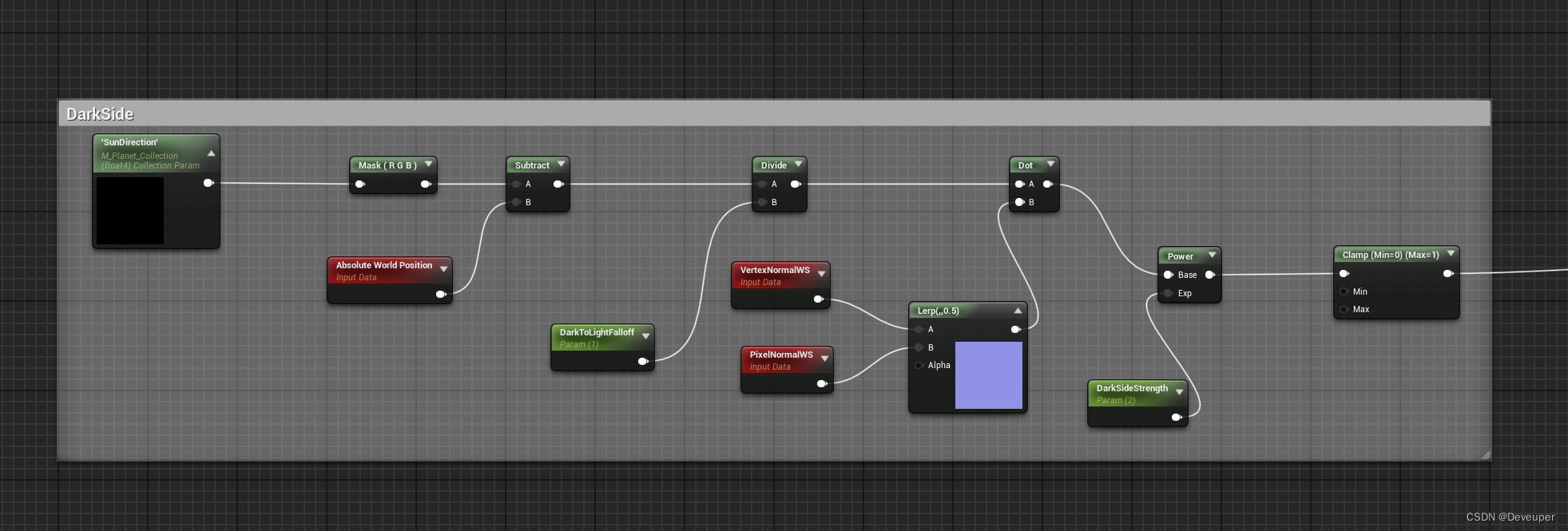
地球行星UE5和UE4
地球行星,包含多种地球风格,可蓝图控制自转和停止,可材质自转. 支持版本4.21-5.4版本 下载位置:https://mbd.pub/o/bread/ZpWZm5lv b站工坊:https://gf.bilibili.com/item/detail/1105582041 _______________________…...

7.k8s中的名称空间namespace
目录 一、Namespace(命名空间) 二、查看系统的名称空间 1.查看系统中的名称空间列表 2.单独查看一个名称空间下的对应资源 三、名称空间的管理 1.创建名称空间 1.1响应式创建 1.2声明式创建 2.删除名称空间 四、资源引用名称空间 一、Namespace(命名空间) 命名空间(Name…...

上海企业源代码防泄密解决方案,企业源代码防泄密如何应对?
随之互联网的发展,企业员工因离职把企业源代码泄露或删库跑路的事情屡见不鲜,各大互联网公司基本都会出现源代码泄露的事情,这样的问题也成了企业在发展过程中不可避免的问题。企业源代码泄露会给企业带来的损失也是不可估量的,据…...

将要上市的自动驾驶新书《自动驾驶系统开发》中摘录各章片段 4
第十三章 车联网 数字化设备正变得越来越普遍并且相互联系。这些设备向数字生态系统智能部分的演进创造了迄今为止尚未解决安全问题的新颖应用。一个特定的例子是车辆,随着车辆从简单的交通方式发展到具有新的感知和通讯功能的智能实体,就成为智能城市的…...

OpenSearch 与 Elasticsearch:7 个主要差异及如何选择
OpenSearch 与 Elasticsearch:7 个主要差异及如何选择 1. 什么是 Elasticsearch? Elasticsearch 是一个基于 Apache Lucene 构建的开源、RESTful、分布式搜索和分析引擎。它旨在处理大量数据,使其成为日志和事件数据管理的流行选择。 Elasti…...

[Docker]容器的网络类型以及云计算
目录 知识梗概 1、常用命令2 2、容器的网络类型 3、云计算 4、云计算服务的几种主要模式 知识梗概 1、常用命令2 上一篇已经学了一些常用的命令,这里补充两个: 导出镜像文件:[rootdocker ~]# docker save -o nginx.tar nginx:laster 导…...
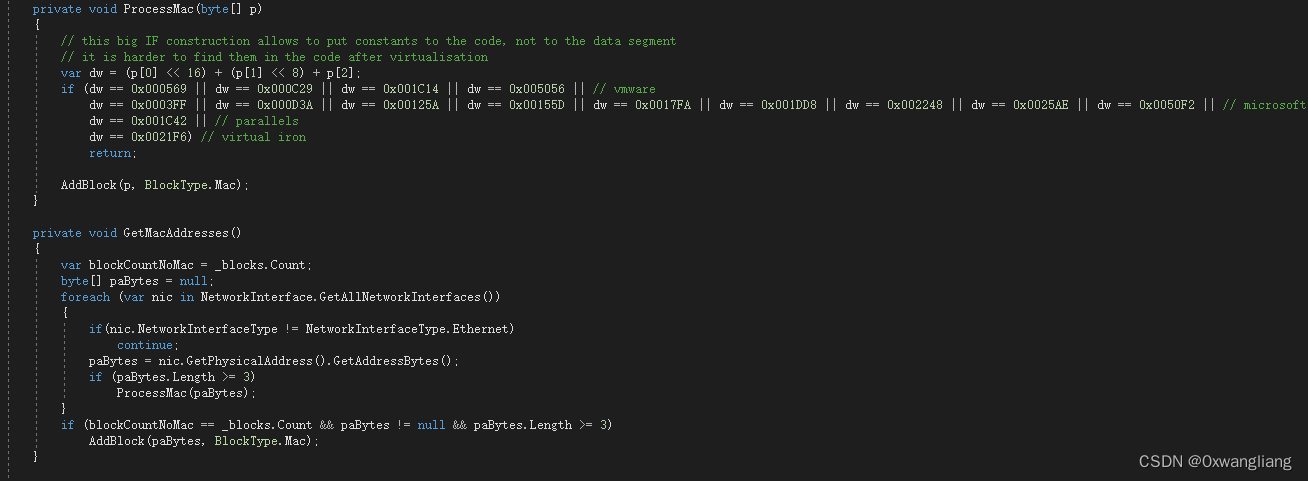
VMP 简单源码分析(.net)
虚拟机 获取CPU的型号 实现了一个指令集解释器,每个操作码对应一个特定的处理函数,用于执行相应的指令操作。在执行字节码时,解释器会根据操作码查找并调用相应的处理函数来执行指令。 截获异常 先由虚拟机处理 处理不了再抛出异常 priva…...

数据结构与算法学习笔记-二叉树的顺序存储表示法和实现(C语言)
目录 前言 1.数组和结构体相关的一些知识 1.数组 2.结构体数组 2.二叉树的顺序存储表示法和实现 1.定义 2.初始化 3.先序遍历二叉树 4.中序遍历二叉树 5.后序遍历二叉树 6.完整代码 前言 二叉树的非递归的表示和实现。 1.数组和结构体相关的一些知识 1.数组 在C语…...

如何在Windows和Linux中杀死Python进程
在开发和运行Python脚本的过程中,有时我们需要强制结束正在运行的Python进程。这可能是因为脚本运行出现了不可预见的错误,或者我们需要停止一个长时间执行的任务。无论原因如何,了解如何在不同操作系统中正确、安全地终止Python进程都是一项…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
