【数学】泰勒公式
目录
引言
一、泰勒公式
1.泰勒公式及推导
(1)推导
(2)公式
2.泰勒中值定理
(1)定理1(佩亚诺余项)
(2)定理2(拉格朗日余项)
(3)两个定理的区别
3.麦克劳林公式
二、常用的泰勒公式
三、泰勒公式核心考点
1.求极限
2.求高阶导
3.证明题
总结
ID:HL_5461
引言
对于任意无穷数,这里以为例,我们可以用多个
的次方将其不断展开,即
类比的,对于一个函数,我们也可以将它写作无穷多x的次方展开,即
这也就是泰勒公式的诞生。
当然就像有限个的次方不能精确表示一个无穷小数一样,上述式子肯定有一定的误差,这个后文讨论。
一、泰勒公式
1.泰勒公式及推导
(1)推导
我们将引言中所写式子记作,所以有:
正如前面所说,这个式子有一定的误差,不能准确表示,所以我们退而求其次,选择让这个式子无限接近
,即
是
的高阶无穷小。
接下来的任务是确定系数。我们先定一个条件:设
在
处n阶可导。
那么如何让非常接近
呢?只需满足两个条件:1.
与
在
处函数值相等;2.
与
在
处直到n阶倒数相等。
我们可以这样理解上面两个条件:函数值相等说明在同一个点处,导数相等说明函数变化一样,值一样变化一样,所以可以近似看作相等。以下是的推导过程:
1
与
在
处函数值相等
,
2
对
与
求一阶导,并带入
,
3
对
与
求二阶导,并带入
,
4
不断求导、总结,所以:
(2)公式
将前面算出的带入
,所以:
由于在引言中说过,如果与
相比有一定误差,所以这里补充一个误差项就能与
相等了。我们将这个误差项称为余项,记作
。
所以泰勒公式就是如下形式:
除了
的前半部分是
在
处的n次多项展开式
称为余项,也是一个误差项
2.泰勒中值定理
泰勒中值定理是对余项的讨论。
(1)定理1(佩亚诺余项)
设
在
处具有直到n阶的导数,则有
其中,
,
称为佩亚诺(Peano)余项。
该展开式称为
在点
邻域的带佩亚诺余项的n阶泰勒公式。
(2)定理2(拉格朗日余项)
设
在包含
的区间
内有直到n+1阶的导数,在区间
上有n阶连续导数,则对任意
时有
其中,
,(
在
与
之间)称为拉格朗日余项。
该展开式称为
在区间
的带拉格朗日余项的n阶泰勒公式。
注:对于拉格朗日余项的泰勒公式,根据定义,题目如果说在区间上有n+1阶的导数,那么做题时需展到n阶,n+1阶留给余项。
(3)两个定理的区别
这里可以结合前面定理内容加粗部分理解
1.成立条件不同。定理2对
的可导性要求更高。2要求区间可导,1只要求点可导;2要求可导至n+1阶,1只要求可导至n阶。
2.x的取值范围不同。定理1需满足
,仅适用于求极限问题;定理2中
可在符合条件的区间
上任取,甚至能取到任意实数,因此中值定理2更广泛地适用于证明题和近成似计算问题。
3.余项形式不同,佩亚诺余项便于求极限,而拉格朗日余项能具体估算近似误差的大小。
3.麦克劳林公式
麦克劳林公式就是令时的泰勒公式:
二、常用的泰勒公式
三、泰勒公式核心考点
1.求极限
方法:按上面给的重要泰勒公式无脑代入
例1:
求极限
将上面式子带入极限:
例2:
设求a,b
代入极限
例3:
设二阶可导,
,求极限
由泰勒公式形式可得:
代入极限:
2.求n阶导数值
方法:依旧上述重要泰勒公式无脑往里代
例1:
求函数在
处的n阶导数
由泰勒公式的唯一性,第n项为
3.证明题
方法:
1.使用拉格朗日余项,对n+1阶可导,展到第n阶
2.和
依题目选择
(证明题比较难,下面讲解会解释思路)
例1:
设在
上二阶可导,且
,求证:
思路:
首先写出公式,因为二阶可导所以展到一阶:
,(
在
与
之间)
由于题目中告知
和
,所以不妨猜测
,代入公式:
在定义域内。
又
代入证毕
这题因为告知导数所以优先猜测
的值,将
代入和相关条件用完之后会发现已经做出来了,所以
的值就无需考虑了
例2:
在
上二阶可导,
,证明
,使得
思路:
首先写出公式,因为二阶可导所以展到一阶:
,(
在
与
之间)
由于题目中未提及导数相关,所以不妨猜测0和1是
,代入公式:
..............1
......2
0和1的相关条件似乎已经用完了
仔细查看上两式,会感觉
的缺少真的很碍眼,难道0和1应该用作
吗?但是如果换作
会发现这样只会减少
一个未知量,并且这样做还会多
一个未知量,好像和上两式没什么区别,所以暂时假定这个思路还是对的,接着往下看(下面是难点)
仔细思考一下
,由于
的缺少所以尽量往
上去想:如何才能有一个
和一个
?结合在区间上的最大值,我们可以联想到极大值。
假定极大值为
,则
,令
取
,则1、2式分别为:
于题目中未提及导数相关,所以不妨猜测0和1是
,代入公式:
..............3
..........4
在
的取值范围内,
和
有确定值,分类讨论能得出
和
的范围
再看题目要求是“存在”,找到一个就OK,所以证毕
这题没有告知导数相关,所以优先猜测
的值,将
代入后发现条件不够,再往后考虑
相关,联系极值,假设并代入,最后可以求得范围
例3:
设在
上二阶可导,且
,其中a,b都是非负常数,证明
思路:
首先写出公式,因为二阶可导所以展到一阶:
,(
在
与
之间)
由于题目中提及
和
,猜测告知条件为
,又加上
在
的取值范围内这一常用隐含条件,则:
到这一步已经条件用完,但是已经无路可走了,所以推翻重来
但是如果改用
,除了泰勒公式原式整个小于等于
啥也做不了,所以再换个思路,试着找点代代
题目没告知什么特殊值,那就只有拿0和1这两个端点试一试了
还是顾及题目给了导数,优先考虑
......................................1
................2
两式相减再取绝对值进行放缩,发现和前面没什么区别,那就改取
.................3
.........4
4-3得:
跟题目要求的
好像有点相像,既然有可能那就先往下做了再说
考虑一下如何把这个碍眼的
替换成题目需要的
(重点)
往定义上想,
是指代确定的
值,但是对于泰勒公式本身,
是可以在定义域上任取的,也就说对定义域上的任意
其实都有上式成立
也就说当
,都有
,这样一来
就成了题目需要的
了
(这里只是为了便于讲解所以放到了后面讨论,写题时可以在写3、4式时直接把
写成
)
对上式取绝对值
然后进行放缩:
把题目给的小于等于条件代入继续放缩:
由于
,继续代入放缩,证毕
这题比较难,还是按照一贯的思路来:因为告知导数所以优先猜测使用
,没用换成
,还是做不出来,继续代值考虑
、
最后发现
可以一试。这题主要还是在于端点值也可以使用这一容易忽视的细节和如何将
考虑作整个定义域上的
值两个难点。
总结
对于泰勒公式题目,首先还是几个重要公式熟背,这样就可以解决大部分题目了。
证明题是泰勒公式的难点,一般使用定理二结合放缩就能解决了,关键在于如何选择和
,这是解决证明题的核心。
若有错误,欢迎大家批评斧正!
相关文章:
【数学】泰勒公式
目录 引言 一、泰勒公式 1.泰勒公式及推导 (1)推导 (2)公式 2.泰勒中值定理 (1)定理1(佩亚诺余项) (2)定理2(拉格朗日余项) …...

C++基础-编程练习题及答案
文章目录 前言一、查找“支撑数”二、数组元素的查找三、爬楼梯四、数字交换五、找高于平均分的人 前言 C基础-编程练习题和答案 一、查找“支撑数” 【试题描述】 在已知一组整数中, 有这样一种数非常怪, 它们不在第一个, 也不在最后一个&…...
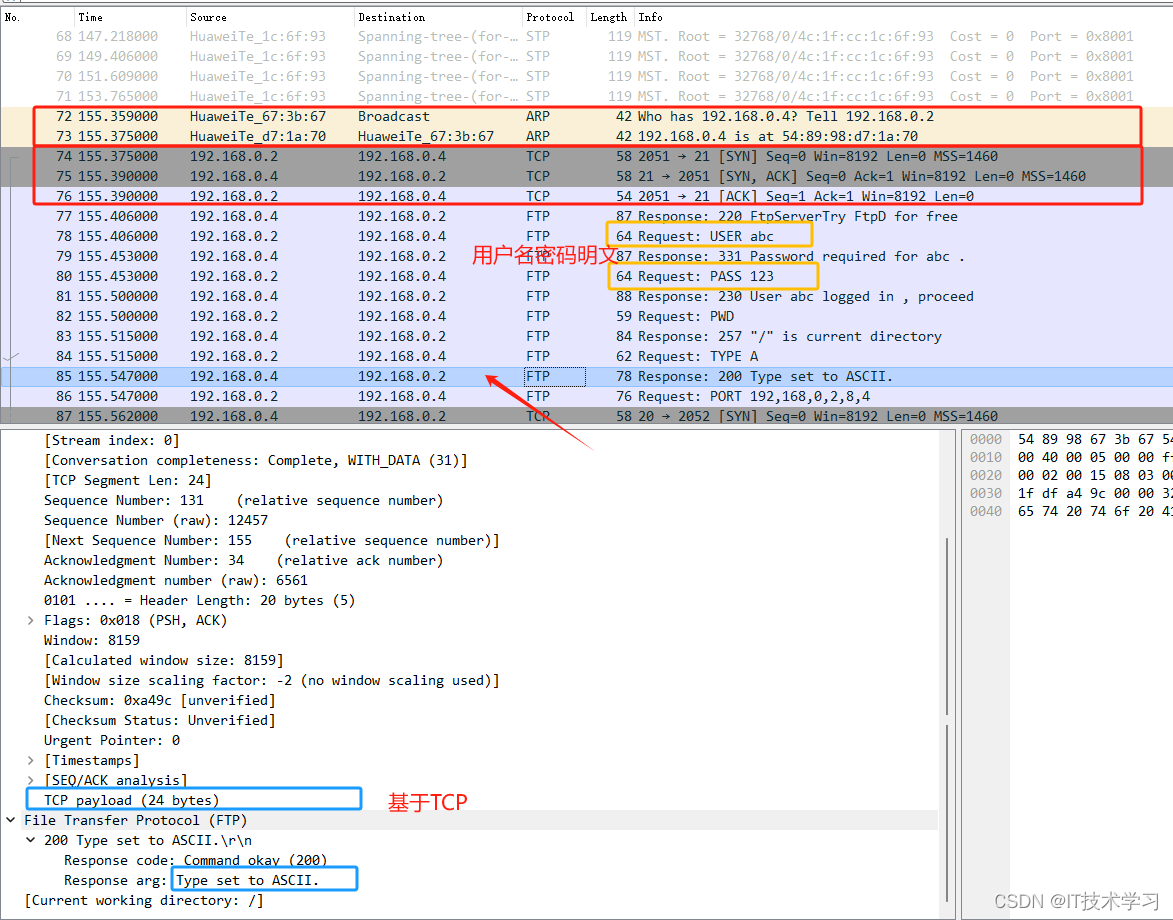
eNSP-抓包解析HTTP、FTP、DNS协议
一、环境搭建 1.http服务器搭建 2.FTP服务器搭建 3.DNS服务器搭建 二、抓包 三、http协议 1.HTTP协议,建立在TCP协议之上 2.http请求 3.http响应 请求响应报文参考:https://it-chengzi.blog.csdn.net/article/details/113809803 4.浏览器开发者工具抓包…...
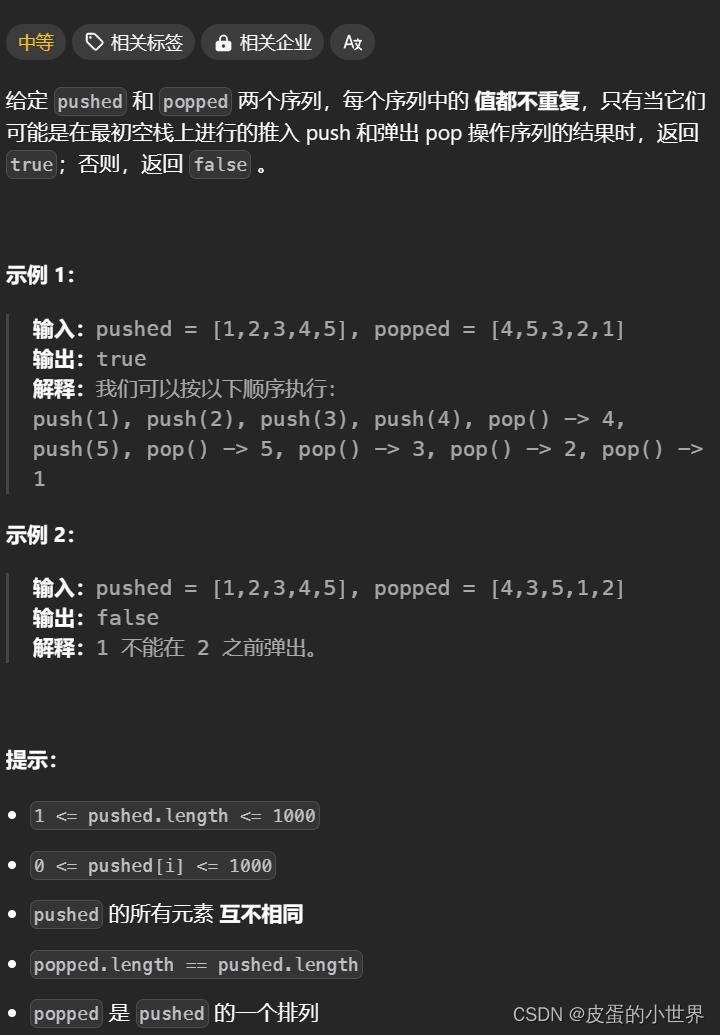
【栈】Leetcode 验证栈序列
题目讲解 946. 验证栈序列 算法讲解 在这里就只需要模拟一下这个栈的出栈顺序即可:使用一个stack,每次让pushed里面的元素入栈,如果当前栈顶的元素等于poped容器中的当前元素,因此就需要让栈顶元素出栈,poped的遍历…...
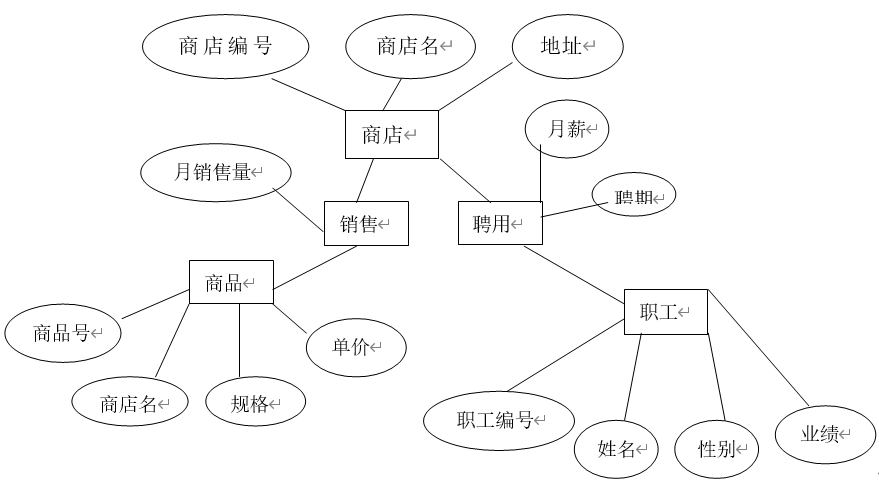
【数据库原理及应用】期末复习汇总高校期末真题试卷08
试卷 一、选择题(每题 2 分,共 30 分) 1. ___ ____是长期存储在计算机内的有组织,可共享的数据集合. A.数据库管理系统 B.数据库系统 C.数据库 D.文件组织 2. 数据库类型是按照 来划分…...
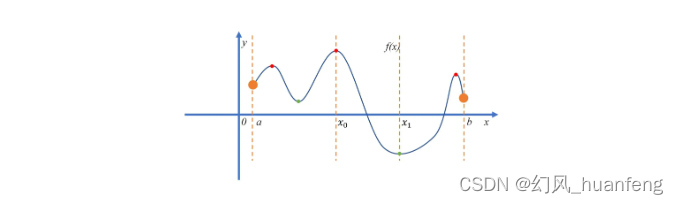
每天五分钟深度学习:数学中的极值
本文重点 在数学领域中,极值是一个极其重要的概念,它不仅在纯数学理论研究中占据核心地位,而且在工程、物理、经济等实际应用领域也发挥着不可替代的作用。极值问题涉及函数的最大值和最小值,是微积分学中的一个基本问题。本文旨在详细介绍数学中的极值概念、性质、求解方…...

【Linux】Linux——Centos7安装Tomcat
1.下载Tomcat 安装包 官网地址:Apache Tomcat - Apache Tomcat 9 Software Downloadshttps://tomcat.apache.org/download-90.cgi 2.将下载的安装包上传到 Xftp 上,我是直接放到 usr 下了 3.将安装包解压到 /usr/local/ tar -zxvf apache-tomcat-9.0.8…...

SpringBoot+vue实现右侧登录昵称展示
目录 1. 定义User数据 1.1.在created方法获取数据 1.2.头部导航栏绑定User数据 1.3.在data中定义User数据 2. 获取数据 2.1.接收父组件传递的值 2.2.展示数据 3. 页面效果 在SpringBoot和 Vue.js 结合的项目中实现右侧登录昵称展示,通常涉及到前端的用户界面…...

【网络原理】UDP协议 | UDP报文格式 | 校验和 | UDP的特点 | 应用层的自定义格式
文章目录 一、UDP协议1.UDP的传输流程发送方接收方 2.UDP协议报文格式:长度受限校验和如何校验:CRC算法:循环冗余算法md5算法: 2.UDP的特点 二、开发中常见的自定义格式1.xml(古老)2.json(最流行…...

NodeJs入门知识
**************************************************************************************************************************************************************************** 1、配置Node.js与npm下载(精力所致,必有精品) …...

代码随想录学习Day 34
62.不同路径 题目链接 讲解链接 动归五部曲: 1.确定dp数组及其下标的含义:dp[i][j]的含义是从(0, 0)走到(i, j)所需的步数; 2.确定递推公式:因为只能往右或者往下,所以dp[i][j] dp[i - 1][j] dp[i][j - 1]。 3.…...
由于找不到MSVCP120D.dll,无法继续执行代码。重新安装程序可能会解决此问题
由于找不到MSVCP120D.dll,无法继续执行代码。重新安装程序可能会解决此问题 一、问题详细描述二、问题产生背景三、问题原因四、解决办法1、安装缺少的库2、直接更换更高版本的opencv 五、vs版本对应vc1、版本对应2、vs对应vc查看方法 一、问题详细描述 同样可能会报 ÿ…...

【前端】输入时字符跳动动画实现
输入时字符跳动动画实现 在前端开发中,为了提升用户体验,我们经常需要为用户的交互行为提供即时的反馈。这不仅让用户知道他们的操作有了响应,还可以让整个界面看起来更加生动、有趣。本文将通过一个简单的例子讲解如何实现在用户输入字符时…...

C语言面试重点问题
1. 冒泡排序法 2. strlen、strcpy、strcat、strcmp的用法和原理 3. 大小端的区分 3.1 主函数区分大小端 #include <stdio.h>int main(void) {int num 0x11223344;char *p (char *)#if (0x11 *p){printf("大端!\n");}else if (0x44 *p){printf(…...

antlr4略解
文章目录 1. antlr4是用来干什么的?2. 什么是lexer和parser?3. 使用antlr4生成某语言的lexer和parser的具体过程4. 其他 1. antlr4是用来干什么的? 是用来生成某语言lexer和parser的。 通俗点说,就是输入一个语言的规则描述文件&…...

超级好用的C++实用库之文件目录操作
💡 需要该C实用库源码的大佬们,可扫码关注文章末尾的微信公众号二维码,或搜索微信公众号“希望睿智”。添加关注后,输入消息“超级好用的C实用库”,即可获得源码的下载链接。 概述 文件和目录操作是操作系统层面上的基…...
结合kimi chat的爬虫实战思路
背景 想钻研一下项目组件,找找之后的学习方向。不能自以为是,所以借着网开源项目网站上公布的项目内容看一下,那些是我可以努力去学习的(入门的)。首先需要获取相关内容,于是爬取整理。 任务1:…...

UnsupportedClassVersionError异常如何解决?
下面是异常报错的详细描述 java -version java version "17.0.11" 2024-04-16 LTS Java(TM) SE Runtime Environment (build 17.0.117-LTS-207) Java HotSpot(TM) 64-Bit Server VM (build 17.0.117-LTS-207, mixed mode, sharing) 环境变量已经是jdk17,但…...

LeetCode热题100|动态规划Part.1|70.爬楼梯、118.杨辉三角、198.打家劫舍
70.爬楼梯 代码随想录原题,看这篇文章:C动态规划Part.1|动态规划理论基础、509.斐波那契数、70.爬楼梯、746.使用最小花费爬楼梯 118.杨辉三角 题目链接:118.杨辉三角 一刷代码 时间复杂度和空间复杂度都造到 O ( n u m R o w s 2 ) O(num…...
python 根据网址和关键词批量下载影像
最近用到了GLASS的LAI产品,但这个产品的文件夹分得很细,我需要的影像又有8个瓦片,一个一个点击很麻烦,于是探索了批量下载的方法 一、下载1幅 import requests import re import os import requests import re# 网页URLurl &…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
