LeetCode:两数之和
文章收录于LeetCode专栏
LeetCode地址
两数之和
给定一个整数数组nums和一个整数目标值target,请你在该数组中找出和为目标值的那两个整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案。
示例 1:
输入:nums = [2, 7, 11, 15], target = 9
输出:[0, 1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1]
示例 2:
输入:nums = [3, 2, 4], target = 6
输出:[1, 2]
示例 3:
输入:nums = [3, 3], target = 6
输出:[0, 1]
题解
第一步审题
给定一个数组求得其中任意两数之和为目标值,题目很简单就是从数组中得得等于目标值的元素的下标。
第二步列出所有解
求解该题目可以采用暴力求解和hash表两种方式。
解法一(暴力枚举)
所谓暴力枚举就是采用两层循环,每层循环取出数组中一个元素,判断两层循环取出的两个元素相加是否等于目标值。
class Solution{public int[] twoSum(int[] nums, int target){for(int i=0; i<nums.length-1; i++){for(int j=i+1; j<nums.length; j++){if(nums[i] + nums[j] == target){return new int[]{i, j};}}}return null;}
}
解法二(hash表)
暴力枚举法采用了两层循环时间复杂度较高,所以可以采用采用的空间换时间的方式,定义一个hash表来记录遍历过程中用过的元素及其下标,这样再下一轮判断的时候可以直接通过map.get(y)= target-x来判断是否等于目标值。
class Solution{public int[] twoSum(int[] nums, int target){Map<Integer, Integer> map = new HashMap<>();for(int i=0; i<nums.length; i++){int sub = target - nums[i];if(map.containsKey(sub)){return new int[]{map.get(sub), i};}map.put(nums[i], i);}return null;}
}
第三步复杂度分析
暴力枚举法使用了两层循环且没有使用额外的内存空间,所以时间复杂度为O(n2),空间复杂度为O(1);hash表使用空间换时间的方法,所以时间复杂度为O(n),空间复杂度为O(n)。
相关文章:

LeetCode:两数之和
文章收录于LeetCode专栏 LeetCode地址 两数之和 给定一个整数数组nums和一个整数目标值target,请你在该数组中找出和为目标值的那两个整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是数组中同一个元素在答案里不能重复出现。…...
CSDN我的创作纪念日128天||不忘初心|努力上进|勇往直前
机缘 Hello,大家好,我是景天,其实很早之前我就加入到了CSND的大军,彼时我还是个刚毕业的小白白,时常过来CSND汲取养料,就这样,慢慢的来提升自己,强大自己。工作锻炼了我,…...

MySQL数据库中的浮点类型和高精度类型有什么区别?为什么不推荐使用浮点类型?
在软件开发中,作为后端,无可避免的需要熟练使用 MySQL 数据库进行数据存储和读取。对于信息系统而言,数据库的的地位不言而喻。那作为软件开发工程师,在使用 MySQL 过程中,又有哪些需要注意的呢?我们从实际…...
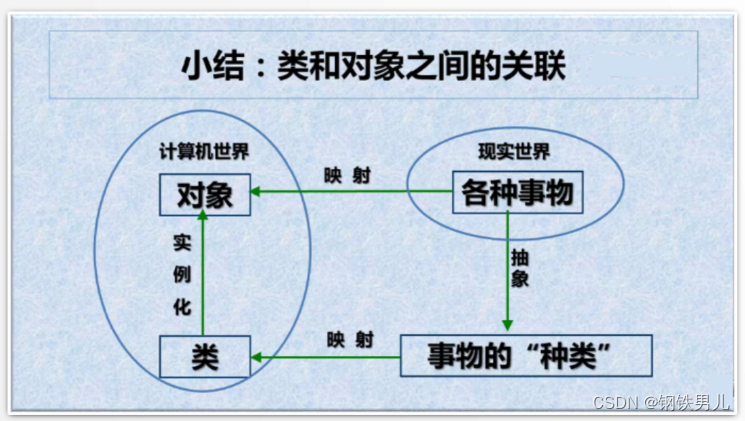
C++ 抽象与封装
一 抽象 抽象实例:时钟 数据抽象: 具有表面当前时间的时、分、秒 行为抽象: 具有设置时间和显示时间两个最基本的功能。 抽象实例:人 数据抽象:姓名、年龄、性别等。 行为抽象: 生物属性:吃…...

antV X6的简要使用教程
🧑🎓 个人主页:《爱蹦跶的大A阿》 🔥当前正在更新专栏:《VUE》 、《JavaScript保姆级教程》、《krpano》、《krpano中文文档》 ✨ 前言 在我们的日常开发工作中,我们经常需要构建复杂的交互式图…...
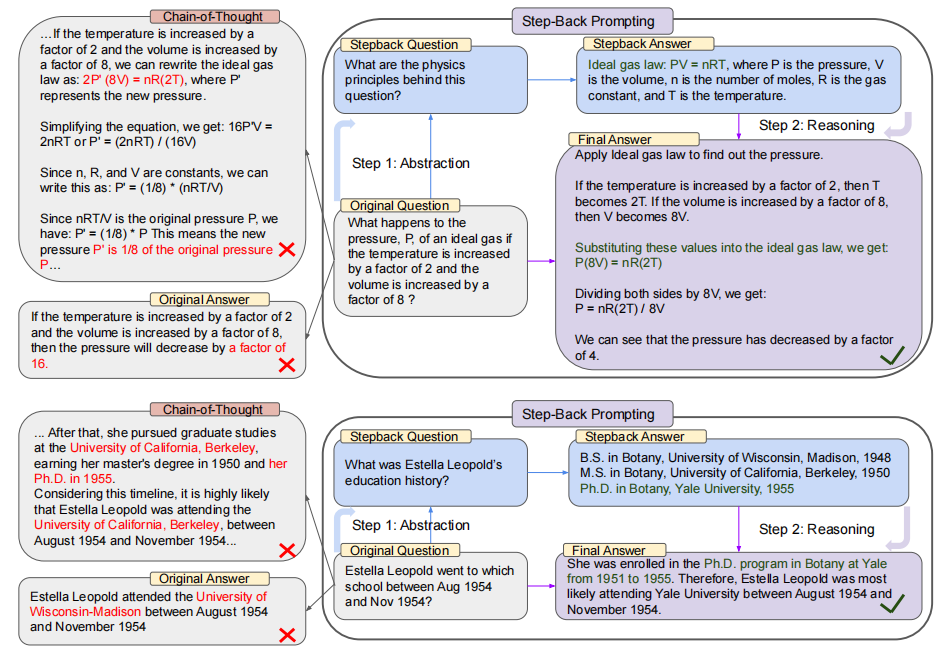
【LLM 论文】Step-Back Prompting:先解决更高层次的问题来提高 LLM 推理能力
论文:Take a Step Back: Evoking Reasoning via Abstraction in Large Language Models ⭐⭐⭐⭐ Google DeepMind, ICLR 2024, arXiv:2310.06117 论文速读 该论文受到的启发是:人类再解决一个包含很多细节的具体问题时,先站在更高的层次上解…...

Java——接口的补充
目录 一:接口的注意事项 1. 接口中不能有方法块; 2. 接口没有构造方法: 3.接口是可以多继承的; 4. 多个接口抽象方法重复 5. 类的父类方法与接口方法重复 二:类与接口 1. 继承与实现 2. 多个父接口的抽象…...

word转pdf的java实现(documents4j)
一、多余的话 java实现word转pdf可用的jar包不多,很多都是收费的。最近发现com.documents4j挺好用的,它支持在本机转换,也支持远程服务转换。但它依赖于微软的office。电脑需要安装office才能转换。鉴于没在linux中使用office,本…...

基于K8S构建Jenkins持续集成平台
文章目录 安装和配置NFSNFS简介NFS安装 在Kubernetes安装Jenkins-Master创建NFS client provisioner安装Jenkins-Master Jenkins与Kubernetes整合实现Jenkins与Kubernetes整合构建Jenkins-Slave自定义镜像 JenkinsKubernetesDocker完成微服务持续集成拉取代码,构建镜…...
PHPStudy 访问网页 403 Forbidden禁止访问
涉及靶场 upload-labd sqli-labs pikachu dvwa 以及所有部署在phpstudy中的靶场 注意:一定要安装解压软件 很多同学解压靶场代码以后访问报错的原因是:电脑上没有解压软件。 这个时候压缩包看起来就是黄色公文包的样子,右键只有“全部提取…...

热爱电子值得做的电子制作实验
加我zkhengyang,进嵌入式音频系统研究开发交流答疑群(课题组) AM/FM收音机散件制作,磁带随声听散件,黑白电视机散件制作,功放散件制作,闪光灯散件制作,声控灯散件,等等,可提高动手能…...

.class文件启动过程以及文件内容结构讲解
当你直接启动一个.class文件时,实际上是在操作系统中调用Java虚拟机(JVM),并将该.class文件传递给JVM以执行。现在让我们来解释一下.class文件的启动过程以及文件内容结构: 启动过程:操作系统通过指定的命…...
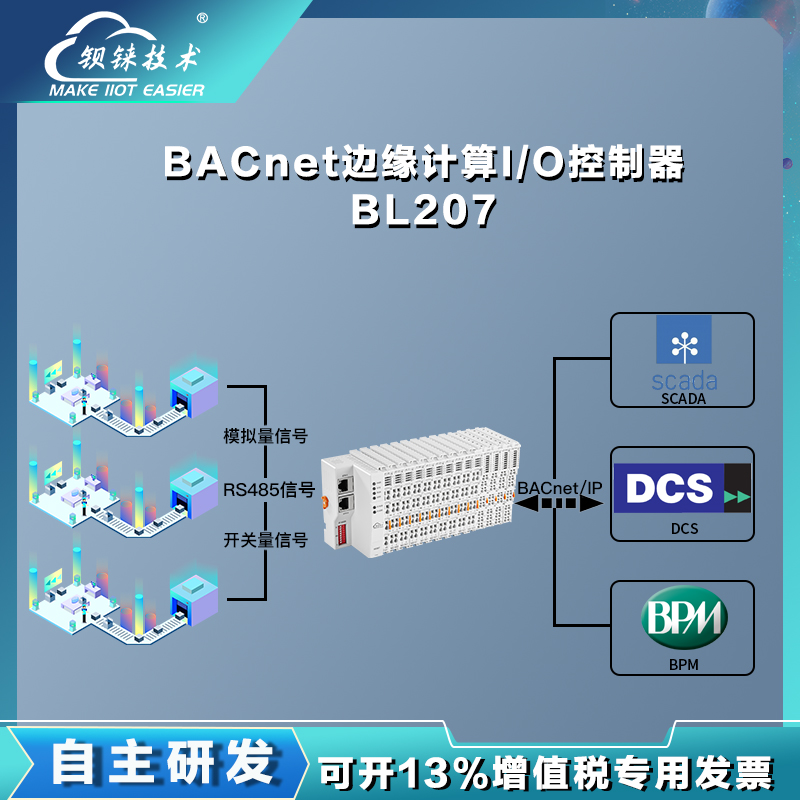
解锁楼宇自动化新维度西门子Insight+BACnet IP I/O控制器
数字城市的楼宇自动化已不再是一个遥不可及的概念,而是成为了现代建筑的标配。特别是在大型商业综合体、高端写字楼和公共设施中,高效的楼宇管理系统是确保环境舒适度与能源效率的关键。当提及楼宇自动化领域的佼佼者,西门子Insight楼宇自动化…...

2024.05.10作业
TCP服务器 头文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTcpServer> #include <QTcpSocket> #include <QList> #include <QMessageBox> #include <QDebug>QT_BEGIN_NAMESPACE namespace Ui { class Widget; …...

基于POSIX标准库的读者-写者问题的简单实现
文章目录 实验要求分析保证读写、写写互斥保证多个读者同时进行读操作读者优先实例代码分析写者优先读写公平法示例代码分析实验要求 创建一个控制台进程,此进程包含n个线程。用这n个线程来表示n个读者或写者。每个线程按相应测试数据文件的要求进行读写操作。用信号量机制分别…...
重生我是嵌入式大能之串口调试UART
什么是串口 串口是一种在数据通讯中广泛使用的通讯接口,通常我们叫做UART (通用异步收发传输器Universal Asynchronous Receiver/Transmitter),其具有数据传输速度稳定、可靠性高、适用范围广等优点。在嵌入式系统中,串口常用于与外部设备进…...
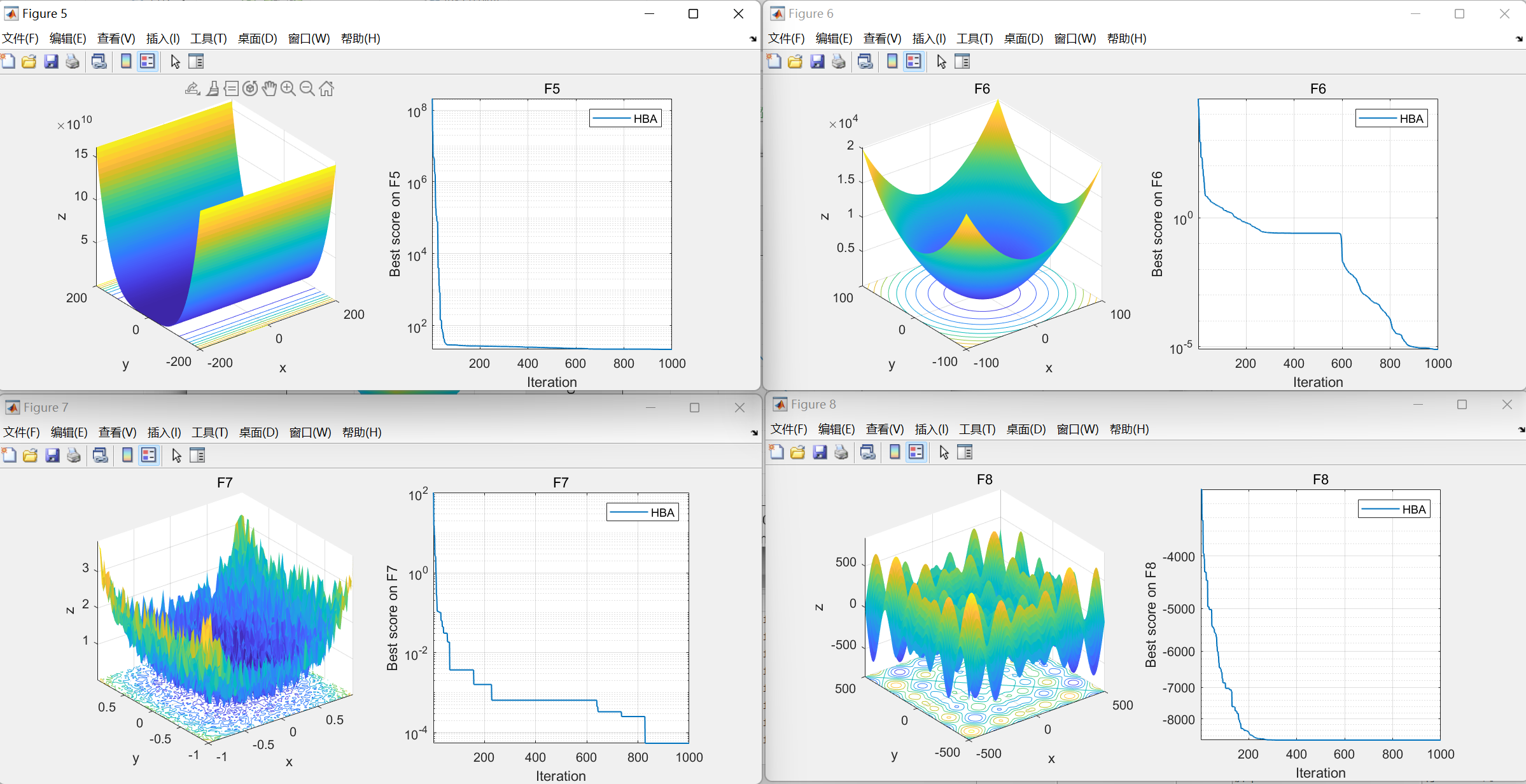
【智能优化算法】蜜獾优化算法(Honey Badger Algorithm,HBA)
蜜獾优化算法(Honey Badger Algorithm,HBA)是期刊“MATHEMATICS AND COMPUTERS IN SIMULATION”(IF 3.6)的2022年智能优化算法 01.引言 蜜獾优化算法(Honey Badger Algorithm,HBA)受蜜獾智能觅食行为的启发,从数学上发展出一种求解优化问题的…...
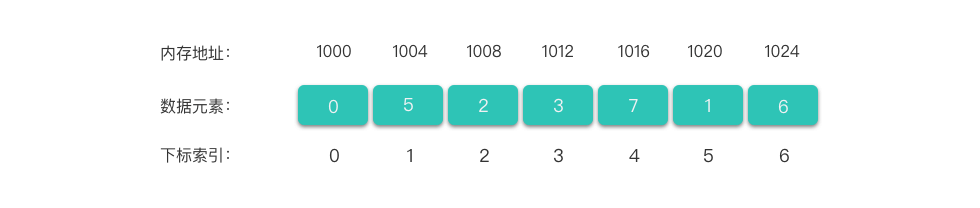
【算法与数据结构】数组
文章目录 前言数组数组的定义数组的基本操作增加元素删除元素修改元素查找元素 C STL 中的数组arrayvector Python3 中的列表访问更改元素值遍历列表检查列表中是否存在某元素增加元素删除元素拷贝列表总结 Python3 列表的常用操作 参考资料写在最后 前言 本系列专注更新基本数…...
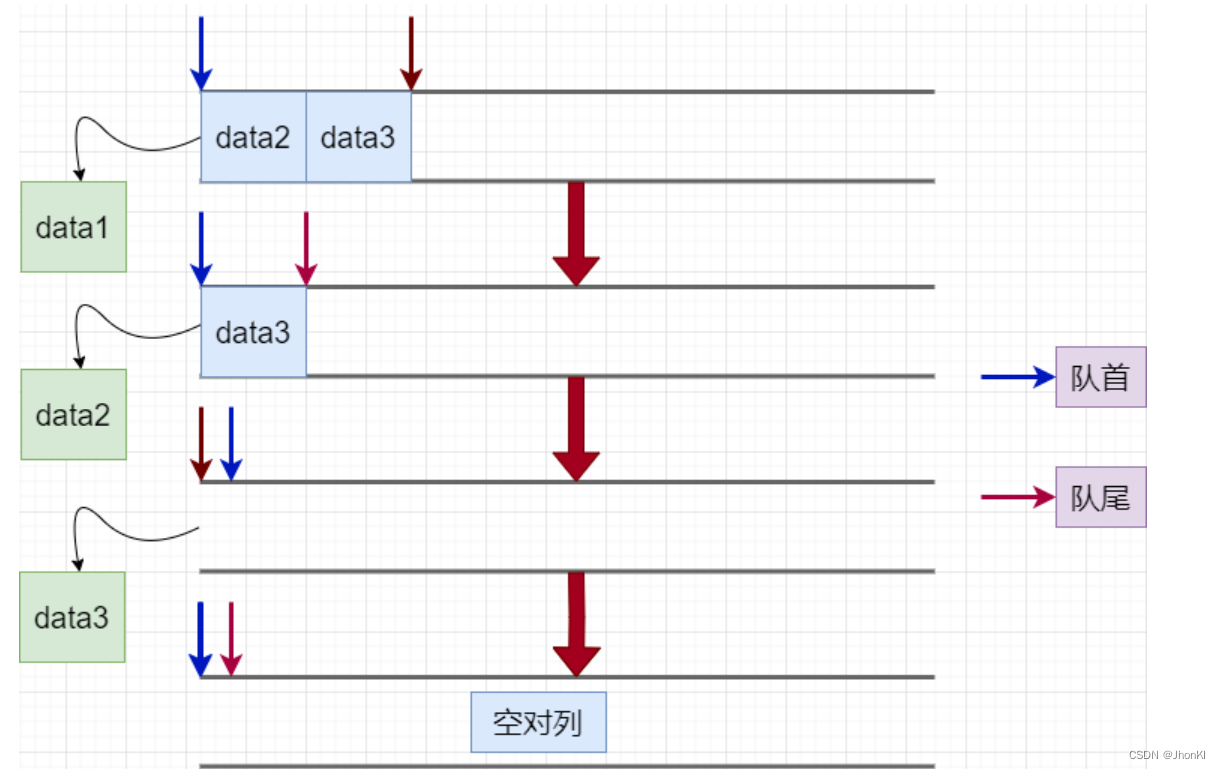
【数据结构】队列详解(Queue)
文章目录 有关队列的概念队列的结点设计及初始化队列的销毁判空和计数入队操作出队操作 有关队列的概念 队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out)入队列:进行插入操作的一端…...
)
Baumer工业相机堡盟工业相机如何通过NEOAPISDK获取相机的Statistics图像传输统计信息(C#)
Baumer工业相机堡盟工业相机如何通过NEOAPISDK获取相机的Statistics图像传输统计信息(C#) Baumer工业相机Baumer工业相机NEOAPI SDK和相机Statistics图像传输统计信息的技术背景Baumer工业相机通过NEOAPISDK获取相机的Statistics图像传输统计信息技术1.引…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
