细说蛮力法(一)
细说蛮力法(一)
- 蛮力法
- 百元买百鸡
- 传统暴力枚举
- 减少无用枚举
- 最优解法
蛮力法
蛮力法通常在算法题中经常用到,也称为暴力枚举,其核心为遍历,即通过列举所有可能的情况,从而得到合适的解。从人的思维角度来看,其实这是一种非常笨的方法。
优点
- 通俗易懂,能后很好的模拟人的思维
- 几乎能够解决所有可计算领域的问题
缺点
- 需要遍历出现的每一种情况,算法时间开销较大
- 适合解决问题规模较小的问题,一旦规模较大,算法时间性能将大大下降
百元买百鸡
这是一个非常经典的循环问题,相信大家在刚学习编程时都会接触到,通俗来讲,就是:
你有100元,现有公鸡5元一只,母鸡3元一只,小鸡1元3只,那么你如何分配所买鸡的种类从而使得鸡数为100且100元恰好花光!
传统暴力枚举
传统思路:我直接枚举每一种方案,只要符合我设置的条件
//假设公鸡数x,母鸡数y,小鸡数z
①x+y+z==100;
②5x+3y+z/3==100
此种情况下,我所得到的各鸡的数量一定是符合要求的
void Chicken(
int x,y;z;
int count-0;
for(x=0;x<=100;x++)//公鸡{for (y=0;y<=100;y++)//母鸡{z=100-x-y;//小鸡if((z%3==0)&&(5*x+3*y+z/3==100))//设置条件{count++;//解的个数count<<"公鸡:"<<x<<"母鸡:"<<y<<"小鸡:"<<z<<endl;}}}if(!count)cout<<"无解"<<endl;
减少无用枚举
再来想,那么每种鸡的数量是不是有个最大值呢?
公鸡5元,我买再多,最多买20只
母鸡3元,最多33只
小鸡=100-公鸡-母鸡
也就是说,各鸡数量不可能超过这个最大值,若超过,一定是不满足条件的,可以直接舍去!!!
void Chicken(
int x,y;z;
int count-0;
for(x=0;x<=20;x++){for (y=0;y<=33;y++){z=100-x-y;if((z%3==0)&&(5*x+3*y+z/3==100)){count++;count<<"公鸡:"<<x<<"母鸡:"<<y<<"小鸡:"<<z<<endl;}}}if(!count)cout<<"无解"<<endl;
最优解法
此处主要运用数学知识来进行简化算法,可见数学在算法中的地位!
根据关系式:
x+y+z=100
5x+3y+z/3=100
可得
①0<=x<=20
②0<=y<=33(必为整数)
所以可推出③47<=z<=100;
根据数学知识转化
3②-1=>*b=25-(7/4)a
由于鸡的数量都是大于等于0的整数,所以a必须是4得倍数。假如num是一个大于等于0的整数则a可表示为4num;则b可表示为25-7num,c可表示为75+3*num
我们根据0<=a<=20;得到num得范围为0<=num<=5;
根据0<=b<=33;得到num得范围为0<=num<=3;
根据c;得到num得范围为0<=num<=8;
所以num的最终范围为0<=num<=3;
for(int num=0;num<=3;++num){cout<<"公鸡:"<<4*num;cout<<"母鸡:"<<25-7*num;cout<<"小鸡:"<<75+3*num<<endl;
}
此解法四次遍历即可搞定,大大降低了时间复杂度,也可以从中看到数学的魅力!!!
相关文章:
)
细说蛮力法(一)
细说蛮力法(一)蛮力法百元买百鸡传统暴力枚举减少无用枚举最优解法蛮力法 蛮力法通常在算法题中经常用到,也称为暴力枚举,其核心为遍历,即通过列举所有可能的情况,从而得到合适的解。从人的思维角度来看&am…...

关于推荐系统的详细介绍
简介推荐系统是一种信息过滤系统,能够自动预测用户对特定产品或服务的偏好,并向其提供个性化的推荐。它通常基于用户的历史行为、个人喜好、兴趣和偏好等,通过数据挖掘和机器学习算法,在大数据的支持下生成个性化的推荐内容&#…...

leetCode刷题笔记
文章目录1. 把两个有序链表整合成一个新的有序列表2. 两数之和3. 有效括号的字符串1. 把两个有序链表整合成一个新的有序列表 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 package com.example.demo.main.Domain; impo…...

数学小课堂:数学和哲学的互动关系(自洽的哲学思想受益于数学思维)
文章目录 引言I 数学是“有底”的学问(止于公理)II 数学对哲学的影响2.1 哲学思想受益于数学思维2.2 笛卡尔的贡献2.3 莱布尼茨的哲学思想III 哲学对数学的影响引言 数学和科学各个分支之间在方法上却具有相通性和普适性,这些通用的方法常常让很多学科同时受益,依靠数学逻…...
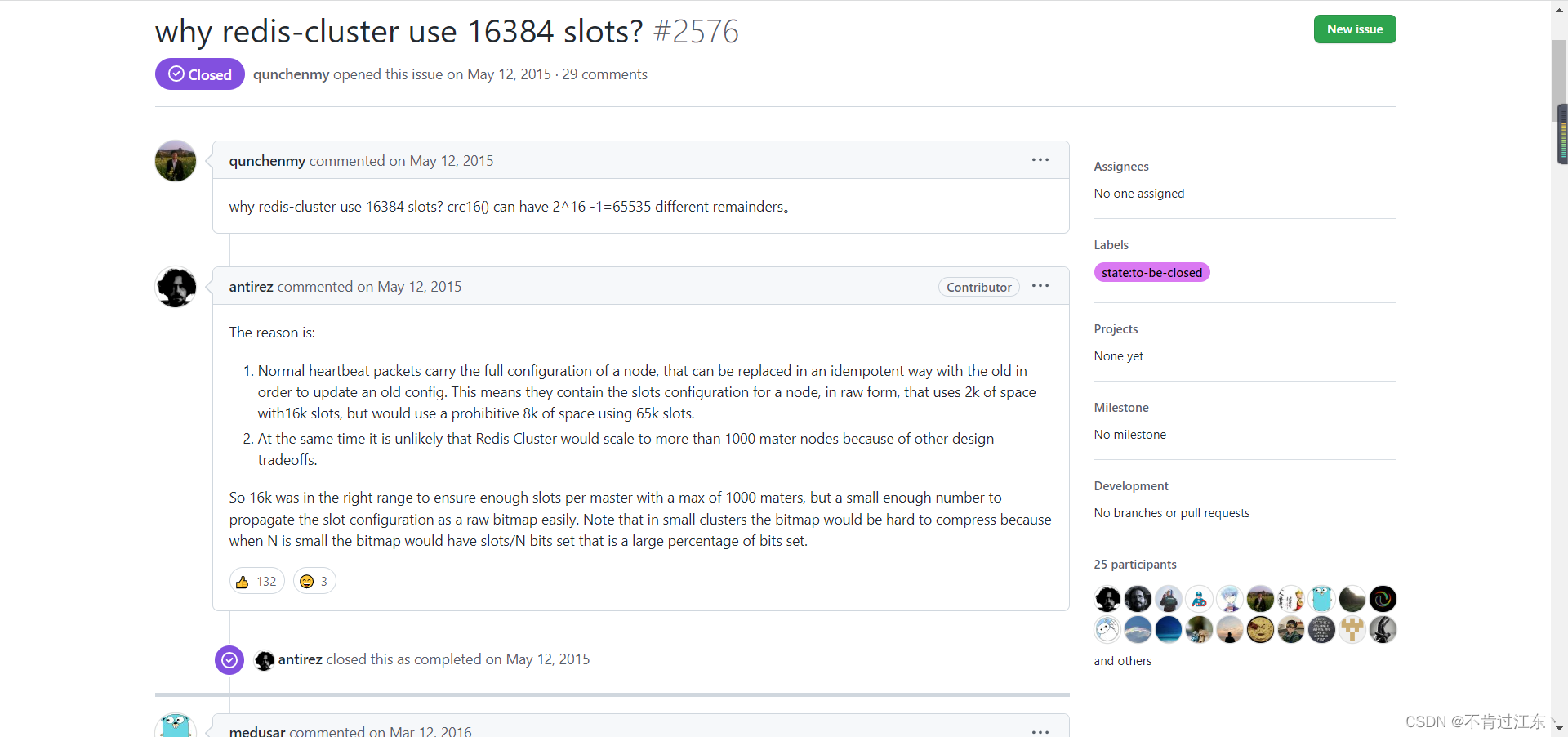
大聪明教你学Java | 带你了解 Redis 的三种集群模式
前言 🍊作者简介: 不肯过江东丶,一个来自二线城市的程序员,致力于用“猥琐”办法解决繁琐问题,让复杂的问题变得通俗易懂。 🍊支持作者: 点赞👍、关注💖、留言Ǵ…...
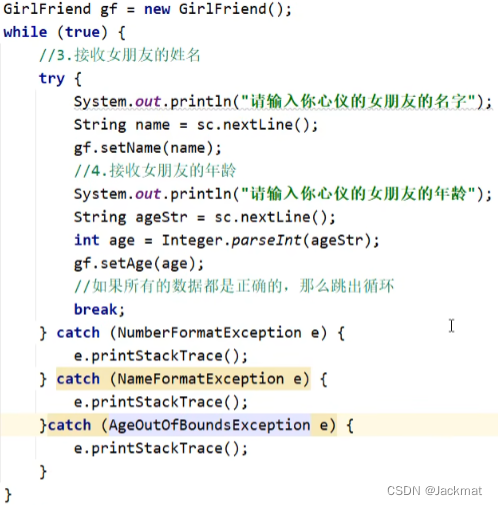
Java中异常(异常的处理方式(JVM默认的处理方式、自己处理(灵魂四问)、抛出异常(throws、throw))、异常中的常见方法、小练习、自定义异常)
编译时异常:在编译阶段,必须要手动处理,否则代码报错(提醒程序员检查本地信息) 运行时异常:在编译阶段是不需要处理的,是代码运行时出现的异常(代码出错而导致程序出现的问题&#…...

液氮恒温器概述
恒温器是直接或间接控制一个或多个热源和冷源来维持所要求的温度的一种装置。 恒温器要实现这种功能,就必须具有一个敏感元件和一个转换器,敏感元件量度出温度的变化,并对转换器产生所需的作用。转换器把来自敏感元件的作用转换成对改变温度…...

Shiro核心——Realm
RealmRealm的作用Realm的实现Realm的配置实例在Shiro中,Realm是一个非常灵活和强大的安全组件,它能够与各种数据源进行集成,满足各种安全需求。通过实现自定义的Realm,我们可以轻松地定制身份验证、授权和加密逻辑,实现…...
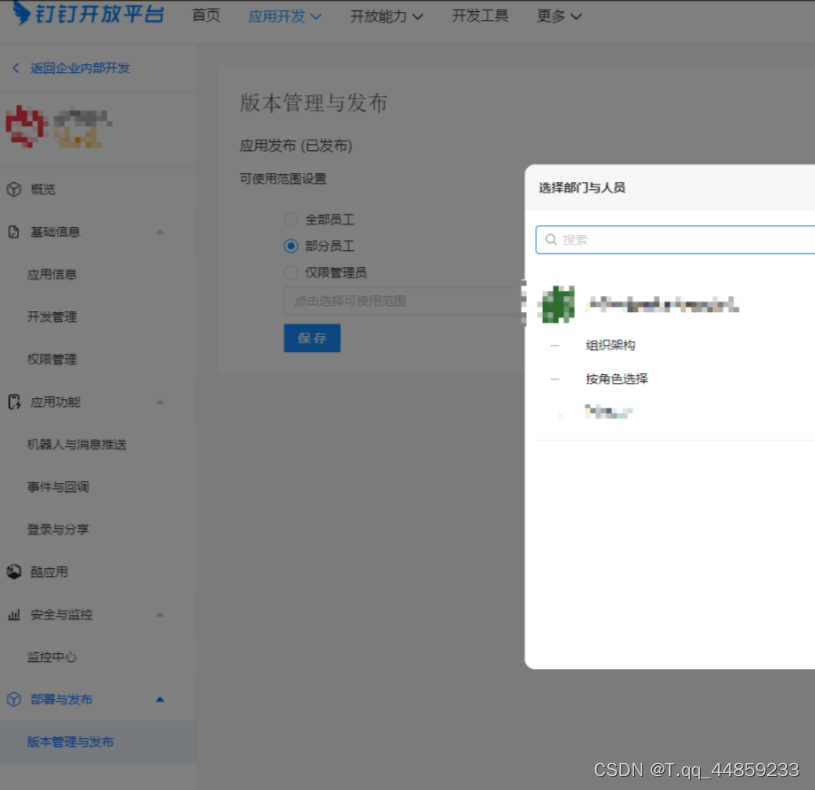
开发钉钉微应用,实现免登+调试
1.创建h5微应用 https://open.dingtalk.com/document/orgapp/develop-org-h5-micro-applications 根据里面的三个步骤,创建h5微应用 2.免登之前必须要先进行JSAPI的授权 文档说明: https://open.dingtalk.com/document/orgapp/jsapi-authentication 根据文档中的说明 步骤…...

0308java基础-注解,反射
一,注解 1.什么是注解: Annotation是从jdk5.0开始引入的新技术作用: 不是程序本身,可以对程序作出解释可以被其他程序读取格式: 以注释名在代码中存在,还可以添加一些参数值SuppressWarnings(value"…...
【鸿蒙应用ArkTS开发系列】- 页面跳转及传参
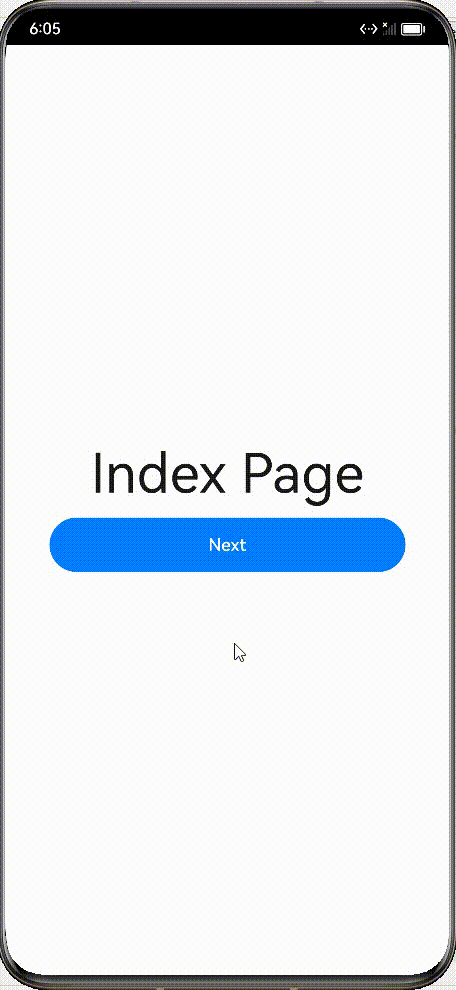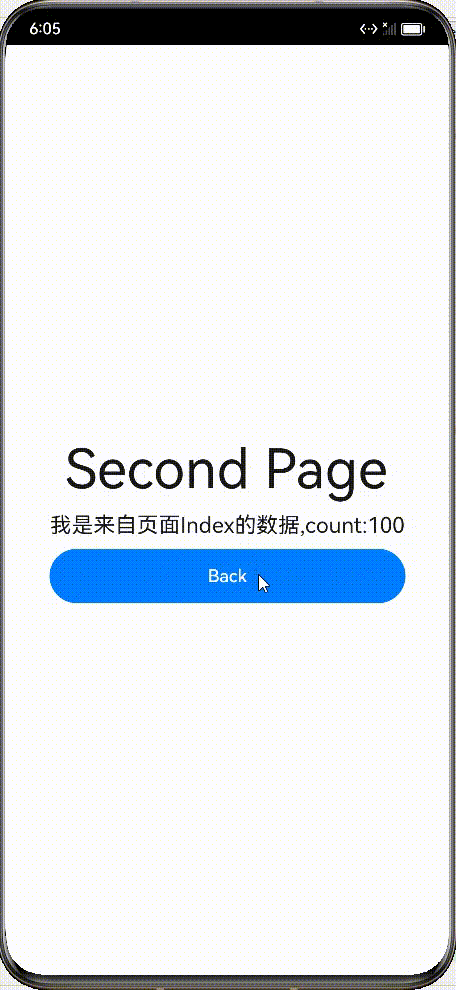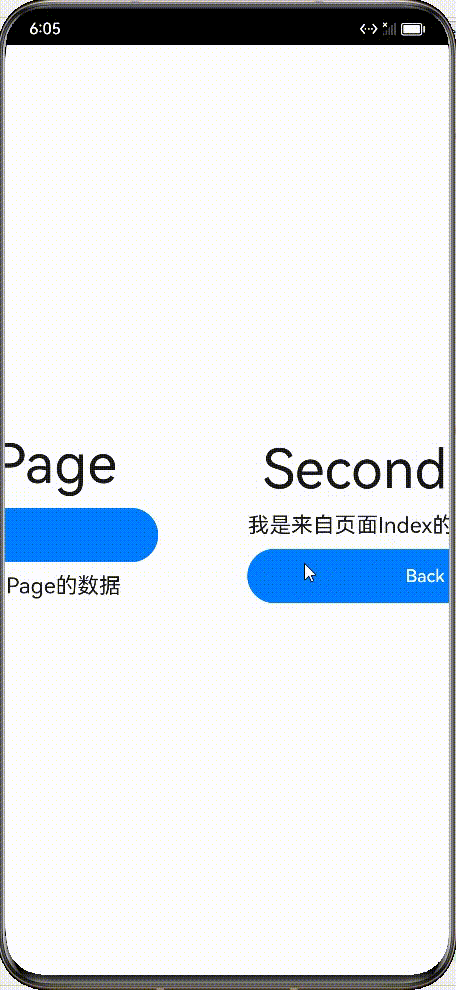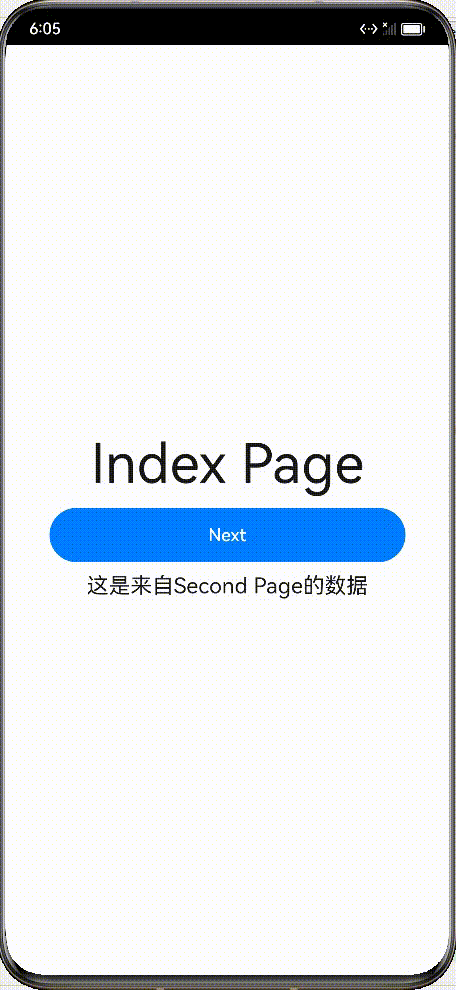
先看下效果图 大致实现的功能点: 从Indext页面跳转到Second页面,传递两个参数,一个字符串,一个数量;Second获取Index页面传递的数据;Second页面点击返回弹窗;Second页面返回携带参数数据&#…...

StringBuilder 类
Java StringBuilder类是一个可变字符串缓冲区,它提供了丰富的方法可以方便地进行字符串操作。与Java StringBuffer类类似,Java StringBuilder类的主要作用是优化字符串的拼接操作,提高代码的效率。在本篇文章中,我们将详细介绍Jav…...

kubectl-k8s用户切换
kubernetes默认使用$HOME/.kube/config配置文件。可以在配置文件中定义多个USER和Cluster的上下文。所以就有两种方式切换用户同一个config中,切换不同用户上下文切换不同的config配置文件同config切换不同用户上下文查看config文件kubeconfig config view查看当前上…...

【面试题】三道面试题让你掌握JavaScript中的执行上下文与作用域以及闭包
前言大厂面试题分享 面试题库前后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库大家好,笔者呢最近再回顾JavaScript知识时,又看到了JavaScript的一些较为常见的内容,仔细看了之后发现…...
计算机网络-- 应用层(day08)
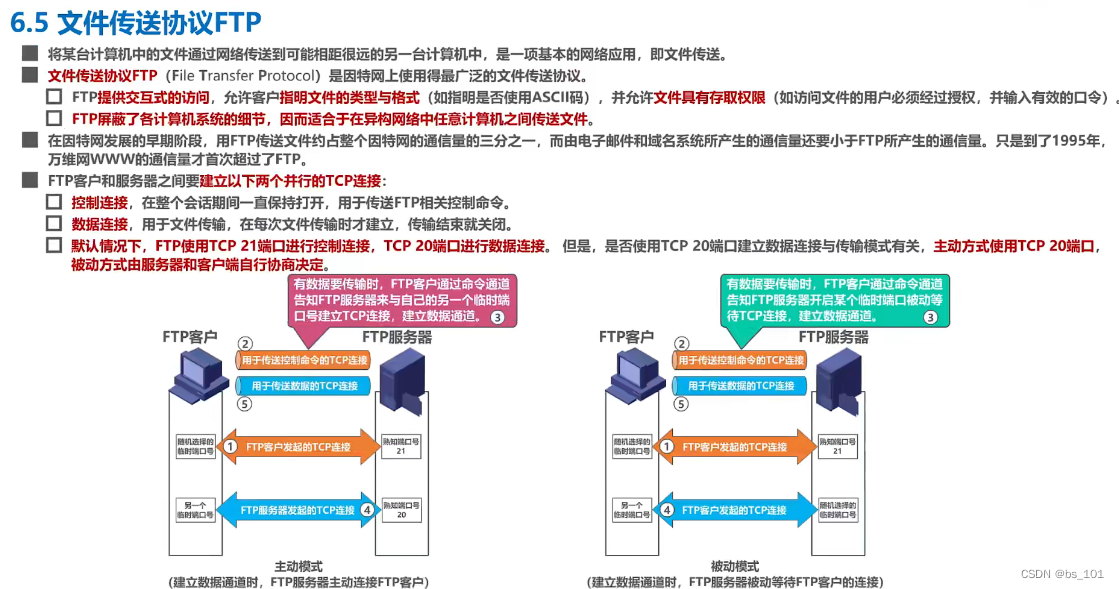
计算机网络两种方式 网络应用程序运行再处于网络边缘的不同端系统上,通过彼此间的通信来共同完成某项任务。 开发一种新的网络应用首先要考虑的问题就是网络应用程序在各种端系统上的组织方式和它们之间的关系。 目前流行的主要有以下两种: 客户/服务器…...

English Learning - L2-5 英音地道语音语调 弹力双元音 [ɪə] [ʊə] [eə] 2023.03.6 周一
English Learning - L2-5 英音地道语音语调 弹力双元音 [ɪə] [ʊə] [eə] 2023.03.6 周一朗读节奏元音的长度元音发音在清辅音和浊辅音前的区别元音发音跟后面浊辅音节数的区别元音在重读音节中复习大小元音发音对比/ʌ/ 舌中音/ɒ/ 舌后音/ʊ/ 舌后音/ɪ/ 舌前音[ɑ:] VS […...
SpringBoot——统一功能处理
处理登陆拦截 上一片博客中讲到SpringAOP可以对页面进行拦截,我们可以用SpringAOP实现对登陆的拦截 但是由于拦截需要HttpSession对象,并且之后还需要页面重定向,因此在实际应用中,并不用SpringAOP进行登陆拦截,而是…...

ORACLE SQL格式化小数点
ORACLE SQL格式化小数点 select CONCAT(TO_CHAR(0.00100,‘990.999’),‘%’) as a0 , CONCAT(TO_CHAR(1100,‘990.999’),‘%’) as a1 , CONCAT(TO_CHAR(0.236100,‘990.999’),‘%’) as a2 , CONCAT(TO_CHAR(0.0200100,‘990.999’),‘%’) as a3 , CONCAT(TO_CHAR(1.0310…...

【信息学奥数】—— 第一部分 C++语言 知识总结
【信息学奥数】—— 第一部分 C语言 知识总结C语言一、C语言入门二、顺序结构程序设计运算符和表达式常量和变量标准数据类型数据输入输出三、控制结构程序设计if语句switch语句四、循环结构程序设计for语句while语句do-while语句五、数组一维数组二维数组字符数组六、函数七、…...
)
video层级过高,以及界面使用多个video时,在安卓APP上同时播放的问题(uniapp)
1、video层级过高的问题 问题一: 我的界面由于是自定义导航栏,所以使用video时,上滑界面video会直在最上层,盖着 头部导航栏 解决方法:使用cover-view,自定义头部使用cover-view替换view 问题二:自定义…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
