对于C++STL及其时间复杂度的总结
由于本次在山东CCPC邀请赛中,对于堆的时间复杂度记忆不清晰,导致第4题没有做出来,与铜牌失之交臂,故觉应整理STL的时间复杂度。
本文仅整理有用(竞赛)的stl及其用法,并且不阐述过于基础的内容。
vector
头文件#include<vector>
vector开在局部或者全局都是开的堆空间,不会爆栈。
也就是说你能把vector开到1e18的长度都没事。
函数
1.vec.front(); //返回第一个元素,时间复杂度O(1)2.vec.back(); //返回最后一个元素,时间复杂度O(1)3.vec.pop_back(); //删除最后一个元素,O(1)4.vec.push_back(x); //在尾部加入一个元素x,O(1)5.vec.size(); //返回vec的长度,O(1)6.vec.begin(); //返回vec的起始位置7.vec.end(); //返回vec的结束位置加一个位置8.vec.empty(); //返回vec是否为空9.vec.clear(); //清空vec,**O(N)**
如果要清空二维vec,就需要循环行数进行clear10.vec.inesrt(pos,x); //在下标pos出插入x元素,**O(N)**
其中pos必须以这样的格式:vec.begin() + n,即插入到n位值(下标从0开始)11.vec.erase(start,end); //删除[first,end)范围内的元素,**O(N)**
创建一维vector
1.普通的创建
vector<数据类型> vec;2.指定长度和初始值的创建
vector<数据类型> vec(长度) //长度被指定,默认值为0
vector<数据类型> vec(长度,默认值); //长度与默认值被指定3.创建默认有多个元素的vector
vector<数据类型> vec{值1,值2,值3}; //创建了长度为3,并填充了三个指定值的vector4.复制创建
(1).
vector<int> a;
vector<int> b(a); //创建出和a有相同数据类型,相同长度,相同初始值的vector,不实用
(2).
vector<数据类型> b = a; //相当于把a数组赋给了b,数据类型要保证相同
创建二维vector
1.指定行数的二维vector
vector<数据类型> vec[N]; //行数不可扩展只能为N,列数可扩展,vec[1]就相当于一个普通一维vector2.行列均可变化的二维vector
vector<vector<数据类型>>vec; //行和列均可扩展,但是必须push_back进去一个完整的数组3.指定行列和默认值
vector<vector<数据类型>> vec(行,vector<数据类型>(列,0));
stack(不如数组模拟)
头文件#include<stack>
创建
stack<数据类型>s;
函数
1.s.push(x); //将x压入栈中,O(1)2.s.pop(); //弹出栈顶,O(1)3.s.top(); //返回栈顶元素,O(1)4.s.empty(); //返回栈是否为空,O(1)5.s.size(); //返回栈元素个数,O(1)
无法直接遍历栈,必须一个个弹出来遍历,当然不如直接用数组模拟能够直接遍历。
queue
头文件#include<queue>
创建
queue<数据类型>q
函数
均为O(1)时间复杂度
1.q.front(); //返回队首元素2.q.back();3.q.push(x);4.q.pop();5.q.size();6.q.empty();
deque
头文件#include<deque>
创建
deque<数据类型>q;
函数
1.q.push_back(x)/q.push_front(x) //压入首/尾,O(1)2.q.back()/q.front() //返回首/尾元素,O(1)3.q.pop_back()/q.pop_front() //O(1)4.q.erase(pos)/q.erase(st,ed) //删除pos处元素或删除[st,ed)的元素,**O(N)**5.q.empty() //O(1)6.q.size() //O(1)7.q.clear() //**O(N)**8.q.insert(pos,x) //**O(N)**
priority_queue
头文件#include<queue>
创建
priority_queue<int>heap 或 priority_queue< int,vector<int>,less<int> >heap; //大根堆,top是最大
priority_queue< int,vector<int>,greater<int> >heap; //小根堆,top是最小
创建对结构体的优先队列时,需要在结构体内定义好排序规则(重载运算符)
struct Node{int a,b;bool friend operator <const (Node &A,Node &B){return A.a < B.a;}
};
函数
牢牢记住优先队列的两个logN,血的教训
1.q.top() //返回堆顶元素,O(1)2.q.push(x) //压入x元素,**O(logN)**3.q.pop() //弹出x元素,**O(logN)**4.q,size() //返回堆中元素数量,O(1)5.q.empty() //O(1)
map/unordered_map
头文件#include<map>及#include<unordered_map>
map基于红黑树,unordered_map基于哈希表
map按照值排序,unordered_map不排序
map的指引可以分成两种,第一种是迭代器,就是下标,第二种是键。
基础用法不赘述
创建
map<数据类型(键),数据类型(值)>map
函数
1.m.find(x) //返回值为key的键,如果没有就返回最后一个下标的下一个值,**O(logN)**2.m.erase(pos) //删除pos位置的键及其值,O(1)3.m.erase(key) //删除key键及其值4.m.size() //返回已经存入了多少个键或值,O(1)5.m.clear() //清空,O(N)6.m.insert({key,value}) //插入元素7.m.rbegin() //返回最后一个元素的迭代器8.m.begin() //返回第一个元素的迭代器9.m.count(key) //查询是否存在键key10.m.lower_bound(x) //返回键大于等于x的第一个键的迭代器,O(logN)11.m.upper_bound(x) //返回键大于x的第一个键的迭代器,O(logN)
对于map,修改和查询都相当于对红黑树进行修改,即时间复杂度都为O(logN),而unordered_map的修改查询操作都接近O(1)
multimap
头文件#include<map>
与map不同的地方在于multimap可以存储多个相同的键及其对应的值
创建
multimap<数据类型(key),数据类型(值)>m
函数
1.m.count(key) //返回键为key的键值对的个数2.m.emplace() //指定位置构建键值对,比insert效率高
大多数函数与map相同,值得注意的是,multimap不能通过直接给出键来查询值。
set/unordered_set
头文件#include<set>以及#include<unordered_set>
并且也有multiset
创建
set<数据类型>s
函数
1.s.begin() //返回第一个元素的迭代器,O(1)2.s.rbegin() //返回最后一个元素迭代器,O(1)3.s.clear() //清空,O(N)4.s.empty() //O(1)5.s.insert() //O(logN)6.s.size() //O(1)7.erase(key) //删除键为key的值,O(logN)8.s.find(x) //查找x,并返回迭代器,O(logN)9.s.count(x) //查询x是否出现过,O(logN)10.s.lower_bound(x) //返回大于等于x的第一个元素的迭代器,O(logN)11.s.upper_bound(x) //返回大于x的第一个元素的迭代器,O(logN)
set可以改变排序方式
set<int>s //从小到大set<int,greater<int>>s //从大到小
string
头文件#include<sring>
特性
支持比较运算符,即可直接按照字典序比较两个字符串,并且更长的更大。
两个字符串可以直接用加法运算法加起来
读入
cin >> str遇到空格就停止
getline(cin,s)遇到换行符停止
函数
1.s.size()/s.length() //返回长度2.s.insert(pos,x) //在pos位置插入字符串x3.s.push_back(x) //在结尾插入字符x,效率较高4.s.erase(pos) //删除pos处的字符5.s.erase(st,ed) //删除[st,ed)中的字符6.s.clear() //清空7.s.replace(pos,len,str) //从pos开始的长度为len替换为字符串str8.s.replace(pos,len,cnt,c) //从pos开始的长度为len替换为cnt个字符c9.s.replace(it1,it2,str) //把从[it1,it2)替换为str10.tolower(s[i]) //字符s[i]变为小写11.toupper(s[i]) //字符s[i]变为大写12.s.substr(pos,len) //截取从pos开始,长度为len的字符串13.s.find(str,pos) //从pos开始查找字符串str或字符14.s.rfind(str,pos) //从pos倒着找字符串str或字符
bitset
头文件#include<bitset>
只能存0和1
创建
1.bitset<n>a //创建n位,每一位都是02.bitset<n>a(s) //用string类型创造bitset
特性
可以像二进制数一样进行位运算
函数
1.b.any() //返回b中是否有1的数位2.b.none() //返回b中是否没有1的数位3.b.count() //返回b中1的个数4.b.size() //返回二进制位有多少5.b[pos] //直接查询pos数位是什么数6.b.set() //把b所有数位设为17.b.set(pos) //把pos数位设为18.b.reset() //b所有数位设为09.b.reset(pos) //bpos数位设为010.b.flip() //b的所有二进制数位取反11.b.flip(pos)12.b.to_ulong() //用b返回一个unsigned long值
array
头文件#include<array>
大小固定,更像普通数组,比vector快
创建
1.array<数据类型,len>a; //开一个len长度的,但是默认值不确定2.array<数据类型,len>a{}; //开一个len长度的,默认值为0
函数
1.a.begin() //返回第一个元素的迭代器2.a.end() //返回最后一个元素后一个位置的迭代器3.a.rbegin() //返回最后一个元素的迭代器4.a.size() //返回a的长度5.a.at(n) //返回a[n]6.a.front() //返回第一个元素7.a.back() //返回最后一个元素8.a.data() //返回一个指向a的第一个元素的指针9.a.fill(x) //用x给a初始化10.a1.swap(a2) //交换相同长度的a1和a2的所有元素11.fill(st,ed,x)//初始化[st,ed)为x12.get<n>(a) //相当于a[1],并且n只能为具体数字
STL函数
这里有众多神器啊
__builtin_ffs(x)
返回x的二进制数位中从后往前找的第一个1所在的位置。
__builtin_popcount(x)
返回x的二进制形式中1的个数
__builtin_ctz
返回x的二进制形式中末尾0的个数(从后往前第一个1之后的)
以上函数都可以在结尾出加上ll来转化为对long long的函数
accumulate(a + st,a + ed,original) O(N)
对取件[st,ed]以original为初始值来求和
并且可以定义函数来定义对结构体的求和方式
atoi(char*) / stoi(string)
把字符串转化为int
fill(a + st,a + ed,value) O(N)
对数组把[st,ed]范围内转化为value值
is_sorted(a + st,a + ed) O(N)
判断数组在[st,ed]范围内是否排序好了
lower_bound(a+st,a+ed,target) / upper_bound(a+st,a+ed,target) O(logN)
在范围内lower_bound查找第一个大于等于target的值,upper_bound查找第一个大于target的值
max_element(a+st,a+ed) / min_element(a+st,a+ed)O(N)
返回数组在范围内的最大值和最小值
nth_element(a+st,a+nth,a+ed)O(N)
返回数组在范围内第nth小的值
next_permutation(a + st,a + ed)O(N)
求下一个字典序大一的排列,并且有返回值,如果是最大的排列就返回false
```prev_permutation(a + st,a + ed)````O(N)
求下一个字典序小一的排列,并且有返回值,如果是最小的排列就返回false
stable_sort()O(NlogN)
与sort一样,只不过不会改变大小相同的元素的位置
to_string
将整数或小数转化为字符串
unique()O(N)
去重
__lg(x)O(1)
求 l o g 2 x log_2x log2x 下取整
相关文章:

对于C++STL及其时间复杂度的总结
由于本次在山东CCPC邀请赛中,对于堆的时间复杂度记忆不清晰,导致第4题没有做出来,与铜牌失之交臂,故觉应整理STL的时间复杂度。 本文仅整理有用(竞赛)的stl及其用法,并且不阐述过于基础的内容。…...

Docker搭建FRP内网穿透服务器
使用Docker搭建一个frp内网穿透 在现代网络环境中,由于防火墙和NAT等原因,内网设备无法直接被外网访问。FRP (Fast Reverse Proxy) 是一款非常流行的内网穿透工具,它能够帮助我们将内网服务暴露给外网。本文将介绍如何在Linux服务器上使用Do…...

【NumPy】掌握NumPy的divide函数:执行高效的数组除法操作
🧑 博主简介:阿里巴巴嵌入式技术专家,深耕嵌入式人工智能领域,具备多年的嵌入式硬件产品研发管理经验。 📒 博客介绍:分享嵌入式开发领域的相关知识、经验、思考和感悟,欢迎关注。提供嵌入式方向…...
您的虚拟机未能继续运行,原因是遇到一个可纠正的错误。请保留挂起状态并纠正错误,或放弃挂起状态。
镜像:应急响应靶机 错误信息 此虚拟机的处理器所支持的功能不同于保存虑拟机状态的虚拟机的处理器所支持的功能。 从文件"E:\XXX.vmss"还原 CPU 状态时出错。 您的虚拟机未能继续运行,原因是遇到一个可纠正的错误。请保留挂起状态并纠正错误…...
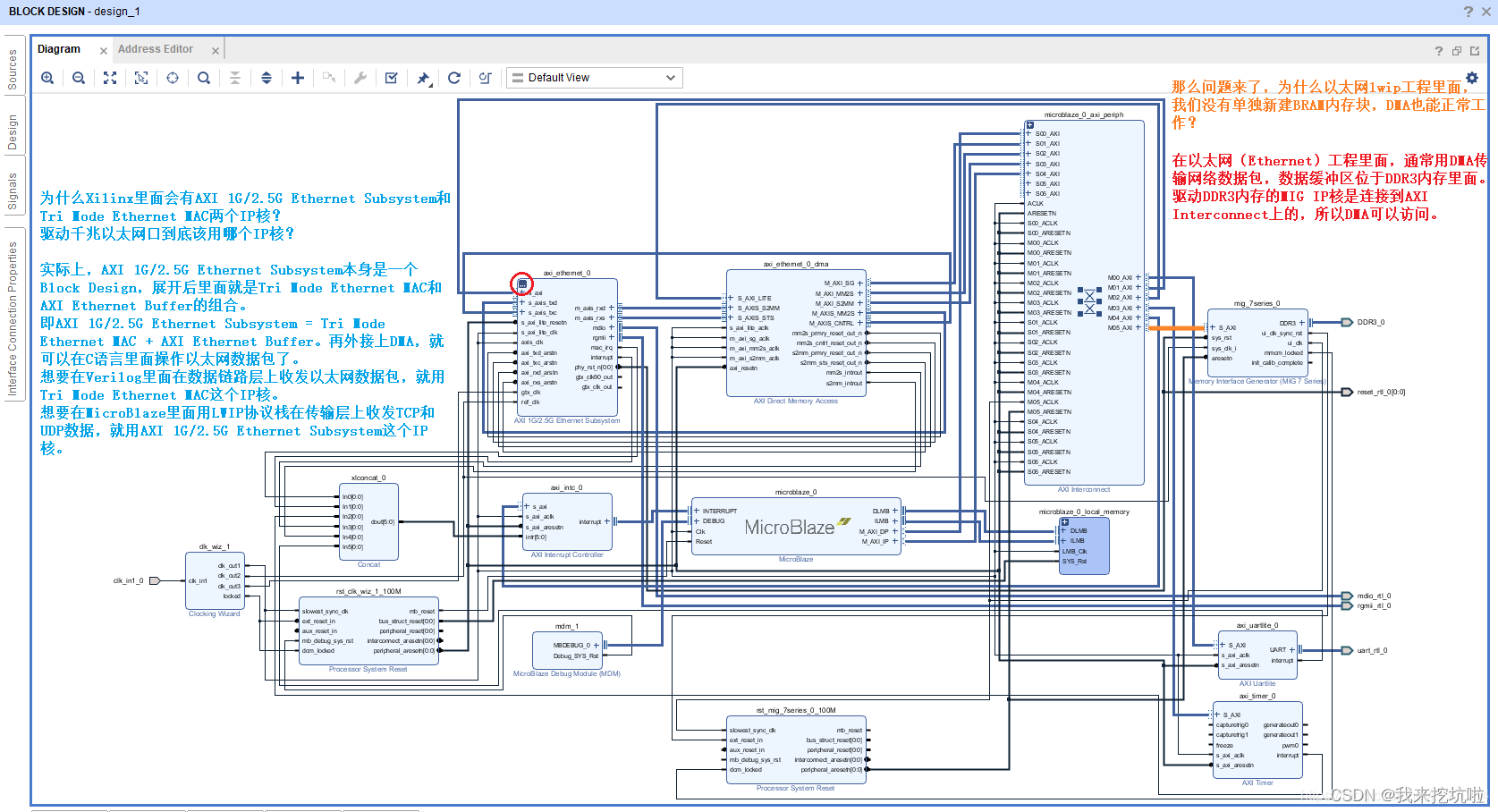
FPGA DMA IP核使用指南
摘要 本文旨在介绍FPGA中DMA(Direct Memory Access)IP核的使用,包括其基本框架、测试代码编写以及仿真波形的分析。DMA是一种允许外围设备直接与内存进行数据交换的技术,无需CPU的介入,从而提高了数据传输的效率。 1. 引言 在现代FPGA设计中,DMA IP核因其…...
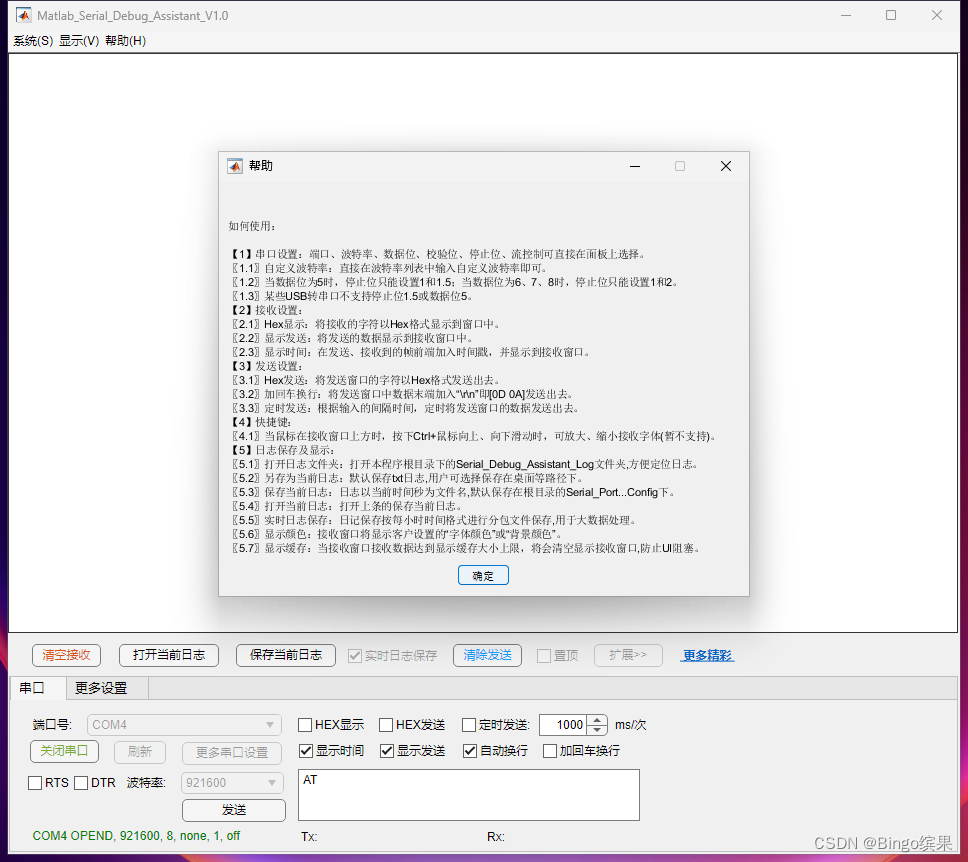
【博客20】缤果Matlab串口调试助手V1.0(中级篇)
超级好用的Matlab串口调试助手 开发工具: MATLAB 2024a中文版 (编程语言matlab) -> Matlab APP Designer 目录 前言 一、软件概要: 二、软件界面: 1.App演示 ---- ◇♣♡♠ ---- 2.其他扩展App展示 编辑 三、获取 >> 源码以及G…...

南京威雅学校:2024年度大戏《Tinkerbell(小叮当)》震撼落幕
三天连演三场 两小时十六幕高潮迭起的舞台故事 一百五十余名师生台前幕后全统筹 逾千名观众现场观演 四个城市五大平台同步直播 南京威雅2024年度大戏 《Tinkerbell(小叮当)》震撼落幕 它以商演级别的舞台设计 宏大而精密的舞台调度 直击心灵的…...

Kotlin 函数
文章目录 函数的定义函数的返回值参数默认值 & 调用时参数指定函数作用域Lambda 表达式匿名函数内联函数扩展函数中缀函数递归函数 & 尾递归函数 函数的定义 函数可以理解成一个小小的加工厂,给入特定的原材料,它就会给出特定的产品。 fun [接…...
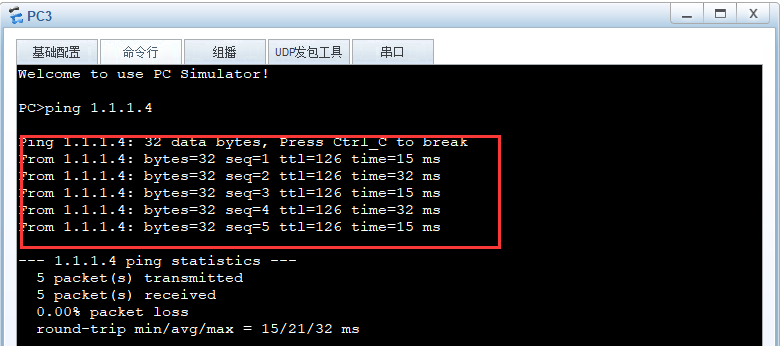
动态路由协议实验——RIP
动态路由协议实验——RIP 什么是RIP RIP(Routing Information Protocol,路由信息协议)是一种内部网关协议(IGP),是一种动态路由选择协议,用于自治系统(AS)内的路由信息的传递。RIP协议基于…...
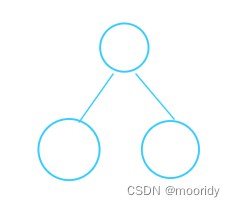
数据结构 | 二叉树(基本概念、性质、遍历、C代码实现)
1.树的基本概念 树是一种 非线性 的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。 把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 有一个特殊的结点,称为根…...

很多Oracle中的SQL语句在EF中写不出来
很多复杂的Oracle SQL语句在Entity Framework(EF)中很难直接表达出来。虽然EF提供了一种方便的方式来使用C#代码查询和操作数据库,但它在处理某些复杂的SQL特性和优化时可能会有局限性。 以下是一些在EF中可能难以直接实现的Oracle SQL功能和…...

浏览器打开PHP文件弹出下载而不是运行代码
说明 使用phpstudy,极少会出现这种情况。 这里主要是帮助大家理解,为什么上传的木马不运行。 问题原因 首先需要理解,访问PHP文件弹出下载,说明服务端的容器(比如Apache或者Nginx)把文件当成了一个普通二…...

安卓自定义UI组件开发流程
安卓自定义ui组件开发流程 开发安卓自定义UI组件的流程大致可以分为以下几个步骤: 确定需求和设计: 确定需要自定义的UI组件的功能和外观。设计组件的交互逻辑和视觉效果。 创建自定义组件类: 创建一个新的Java类,继承自View、V…...
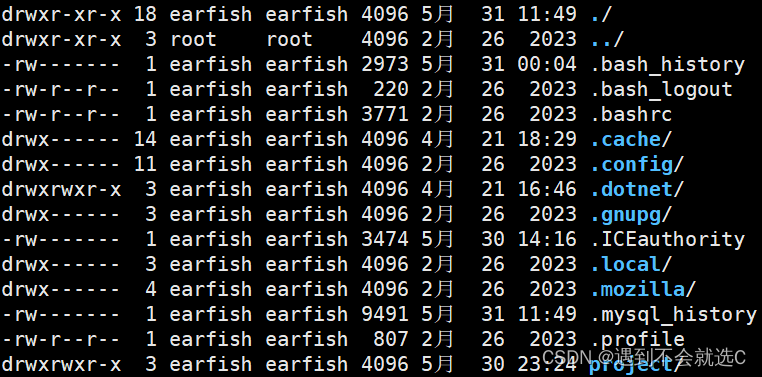
【LINUX】LINUX基础(目录结构、基本权限、基本命令)
文章目录 LINUX的目录结构LINUX的基本权限LINUX基本命令 LINUX的目录结构 /:表示根目录bin:存放二进制可执行文件(命令ls、cat、mkdir等)boot:存放系统引导文件dev:存放设备文件etc:存放系统配置文件home:…...

Aigtek功率放大器的主要性能要求有哪些
功率放大器是电子系统中的重要组件,用于将低功率信号放大到高功率水平。功率放大器的性能直接影响到信号的放大质量和系统的整体性能。下面西安安泰将介绍功率放大器的主要性能要求。 增益:功率放大器应当具有足够的增益,即将输入信号的幅度放…...
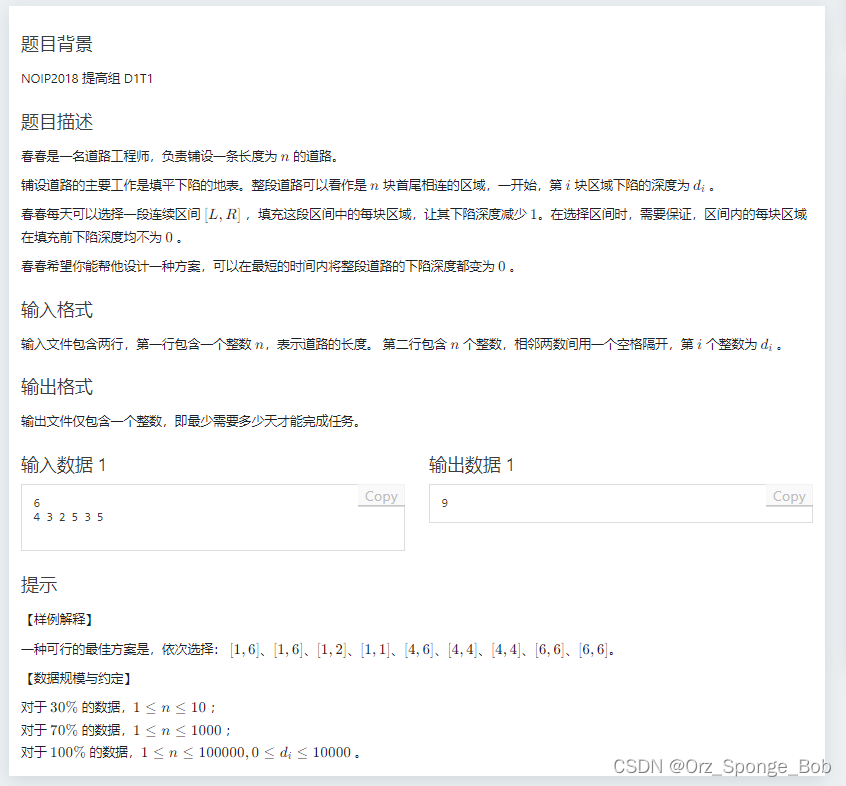
2024.5.29晚训参考代码
因为本套题没有BFS例题,所以我先把BFS模板放着 #include<bits/stdc.h> using namespace std; int n,m;//n*m的棋盘 int dis[402][402]; bool vis[402][402]; int X[]{-2,-2,-1,-1,1,1,2,2};//偏移量的表 int Y[]{-1,1,-2,2,-2,2,-1,1};//定义一个数组&…...
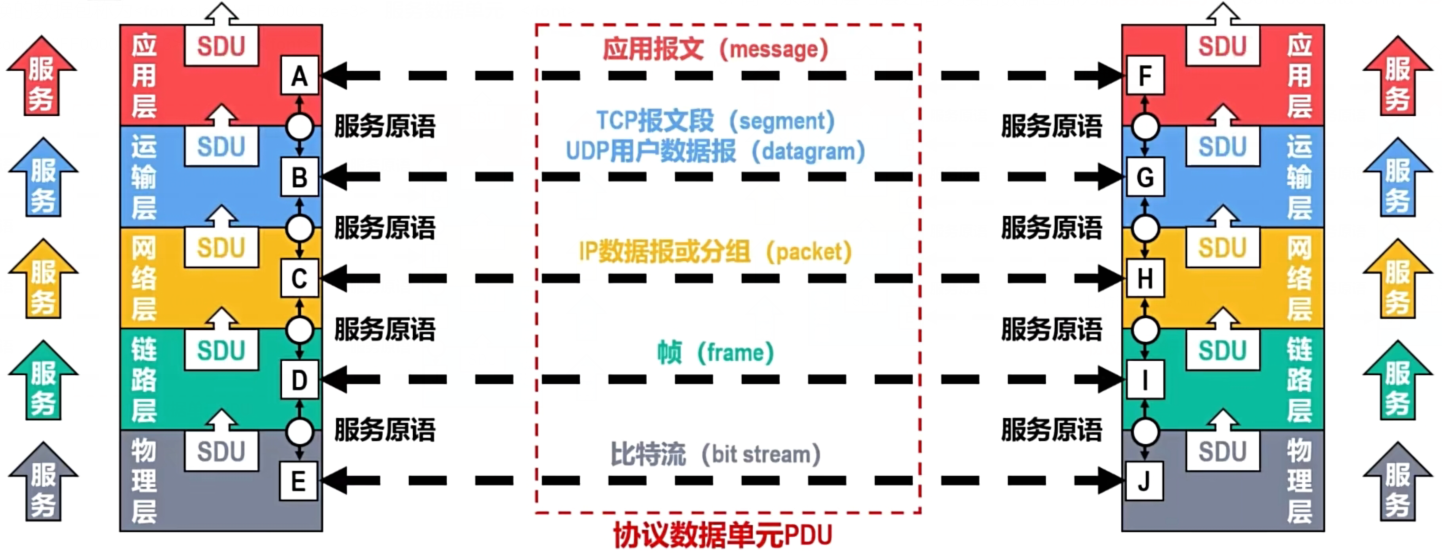
【计算机网络】——概述(图文并茂)
概述 一.信息时代的计算机网络二.互联网概述1.网络,互连网,互联网(因特网)1.网络2.互连网3.互联网(因特网) 2.互联网简介1.互联网发展的三个阶段2.互联网服务提供者(ISP)3.互联网的组…...
C语言多个源程序编译的CMakeList文件编写/源程序生成动态库
1.编译多个源程序时CMakeLists文件编写 1.若源程序目录结构如下: main.cpp中include“LCD_2inch4.h”头文件,而LCD_2inch4.h中include其它源程序,则CmakeLists.txt文件可为如下: # 设置项目名称 cmake_minimum_required(VERSI…...

C# list集合
一、list集合基本使用 1.添加元素 ① 单个元素添加 List<int> list new List<int>();for (int i 0; i < 3; i){list.Add(i);}//输出:0,1,2 ②初始化时添加元素 List<int> list2 new List<int> { 1, 2, 3 };//输出:0,1…...

****三次握手和四次挥手
一、三次握手 1.简要描述TCP三次握手的过程 第一次握手,客户端发送SYN包到服务器; 第二次握手,服务器收到SYN包,回复一个SYNACK包; 第三次握手,客户端收到服务器的SYNACK包后,回复一个ACK包…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
