【1800】【5.22-5.24】
E1. String Coloring (easy version)
E2. String Coloring (hard version)
【细节参考了题解】
题意:序列拆分为最少的若干条不降序列。
思路:简单版可以 n 2 n^2 n2 dp。定义 b o o l d p ( i , j ) bool ~dp(i, j) bool dp(i,j) 表示是否存在方案使得两个序列最终位置为 i , j i, j i,j 。自己定义的时候定义得很麻烦。
还有贪心的思路,类似二分求lis,维护一个序列 l s ls ls ,表示当前第 i i i 个序列的末尾值是多少,并降序排序(方便新增加序列)。贪心的找到第一个序列,然后放下当前增量的字符。
AC代码(dp):https://codeforces.com/contest/1296/submission/262129471
AC代码(贪心):https://codeforces.com/contest/1296/submission/262130727
E. Increasing Subsequences
思路:容易想到二进制拆分,划分为 l o g log log 个长度为 l o g log log 的 lis 。这样显然不满足限制。考虑如何重复利用使得 lis 交集更大,可以先构造一个 lis ,如果要继续增加 2 k 2^k 2k 个lis,那么利用原 lis 的一个后缀即可。注意插入的位置。
AC代码:https://codeforces.com/contest/1922/submission/262134310
D. Zookeeper and The Infinite Zoo
思路:首先考虑到,一次操作可以拆分为若干子操作: u = u + 2 k ( u & 2 k = 2 k ) u=u+2^k(u\&2^k=2^k) u=u+2k(u&2k=2k) 。这样的话就相当于把 u 的二进制 1 向高位移动,1 的数量不会增多。判断是否可以配对即可。也可以前缀和。
AC代码:https://codeforces.com/contest/1491/submission/262154328
D. Letter Picking
【看了洛谷的 tag 】
思路:区间 dp 。难点在于博弈决策。只考虑长度为偶数的局面,即 a 面对的局面。先考虑 a 是否有策略能赢,否则考虑是否有策略能平手,否则就输了。
AC代码:https://codeforces.com/contest/1728/submission/262276717
D. Lucky Permutation
思路:这道题思路也是比较典。考虑置换环,如果一个环上有编号相邻的节点,那么余下这一对即可;否则,都拆为孤立点,然后随便连上两个点即可。
AC代码:https://codeforces.com/contest/1768/submission/262351844
D. Range = √Sum
思路:好长时间憋出来的。首先偶数好考虑。如何考虑奇数?开始找性质,假设 a 1 = 1 a_1=1 a1=1 ,发现 a n a_n an 和 n n n 大概是同阶的。先考虑 = n 2 =\sqrt {n^2} =n2 ,发现构造不出来。最后打表发现某种方法可以构造出 = 4 × n 2 =\sqrt{4\times n^2} =4×n2 。遂过。
AC代码:https://codeforces.com/contest/1758/submission/262357393
D. Take a Guess
思路:这题我是拆位转化为 01 序列求解的,查询次数 2 × n − 1 2\times n - 1 2×n−1 但特别麻烦。
利用到性质就非常好写了。划重点: ( x & y ) + ( x ∣ y ) = x + y (x \& y)+(x|y)=x+y (x&y)+(x∣y)=x+y 。这样的话就好构造了,查询次数 2 × n 2\times n 2×n ,方法见题解。
AC代码(拆位):https://codeforces.com/contest/1556/submission/262366785
AC代码(性质):https://codeforces.com/contest/1556/submission/262370912
相关文章:

【1800】【5.22-5.24】
E1. String Coloring (easy version) E2. String Coloring (hard version) 【细节参考了题解】 题意:序列拆分为最少的若干条不降序列。 思路:简单版可以 n 2 n^2 n2 dp。定义 b o o l d p ( i , j ) bool ~dp(i, j) bool dp(i,j) 表示是否存在方案…...
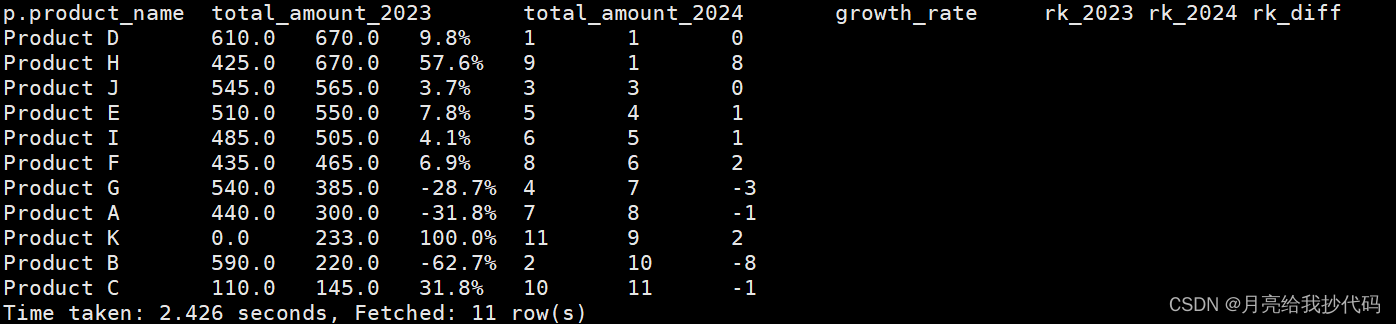
统计各个商品今年销售额与去年销售额的增长率及排名变化
文章目录 测试数据需求说明需求实现分步解析 测试数据 -- 创建商品表 DROP TABLE IF EXISTS products; CREATE TABLE products (product_id INT,product_name STRING );INSERT INTO products VALUES (1, Product A), (2, Product B), (3, Product C), (4, Product D), (5, Pro…...
)
华为校招机试 - 矿车运输成本(20240522)
题目描述 露天矿采矿作业的特点是规模大,矿石和废料的移动量达到百万吨,运输成本开销较大,需要寻求一种最优的运输路径节省成本。 已知矿场可以划分成 N * M 的网格图,每个网格存在地形的差异,因此通过不同网格时,成本开销存在差异。 网格有以下 5 种类型: 标志为 S …...
)
【C++奇技淫巧】CRTP(奇特重现模板模式)
CRTP(Curiously Recurring Template Pattern,奇特重现模版模式),是一种在C中使用模板来实现的设计模式,主要用于实现编译时多态性(静态多态)。这种模式通过类模板和模板继承机制来实现,使得派生…...
)
web学习笔记(六十一)
目录 如何使用公共组件来编写页面 如何使用公共组件来编写页面 1.导入公共组件nav.vue import Catenav from "/components/nav.vue"; 2.在页面插入子组件 如果使用了setup语法糖此时就可以直接在页面插入 <Catenav ></Catenav>标签, …...

Nginx在Docker中的应用:容器化部署与扩展
在当今的云计算和微服务时代,Docker容器技术因其轻量级、可移植性和可扩展性而受到广泛关注。Nginx,作为一个高性能的HTTP和反向代理服务器,也在Docker中找到了其广泛的应用场景。本文将探讨Nginx在Docker中的容器化部署和扩展策略࿰…...

vscode编译和调试wsl环境的c语言程序
直接f5会报错,提示你改一下json文件 launch.json { “version”: “0.2.0”, “configurations”: [ { “name”: “(gdb) Launch”, “type”: “cppdbg”, “request”: “launch”, “program”: “ w o r k s p a c e F o l d e r / a . o u t " , " …...
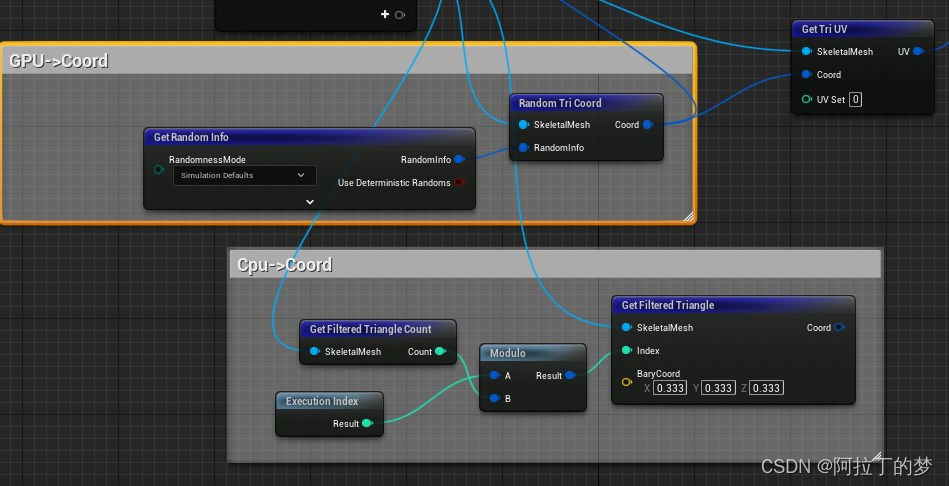
(CPU/GPU)粒子继承贴图颜色发射
GetRandomInfo节点(复制贴进scratch pad Scripts) Begin Object Class/Script/NiagaraEditor.NiagaraClipboardContent Name"NiagaraClipboardContent_22" ExportPath/Script/NiagaraEditor.NiagaraClipboardContent"/Engine/Transient.NiagaraClipboardConten…...

【C#】 一个窗体能够显示、最小化、最大化、关闭时分别触发方法
在C#的WPF应用程序中,窗体(即继承自System.Windows.Window的类)能够通过处理以下事件来响应显示、最小化、最大化和关闭操作: 1.显示: 窗体显示时没有直接对应的事件,但你可以通过覆盖OnLoaded方法或订阅…...

pgsql基本操作
查看已经存在的数据库 postgres# \lList of databasesName | Owner | Encoding | Collate | Ctype | Access privileges ----------------------------------------------------------------------postgres | postgres | UTF8 | C | C | runoobdb …...
3d渲染的常用概念和技术,渲染100邀请码1a12
之前我们介绍了3D渲染的基本原理和流程,这次说下几个常用概念和技术。 3D渲染中涉及到很多专业的概念和技术,它们决定了渲染质量和效果,常用的有以下几个。1、光线追踪 光线追踪是一些专业渲染器(如V-Ray和Corona等)…...
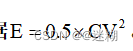
热敏电阻的设计
热敏电阻(NTC)的作用:抑制开机时的浪涌电流。防止开机瞬间产生的浪涌电流损坏后面的元件。 取值依据:根据对开机的脉冲电流(浪涌电流)小于多少A? 由,这个U是指最大输入电压,I为要求的浪涌电流。 NTC是负温度系数的热…...
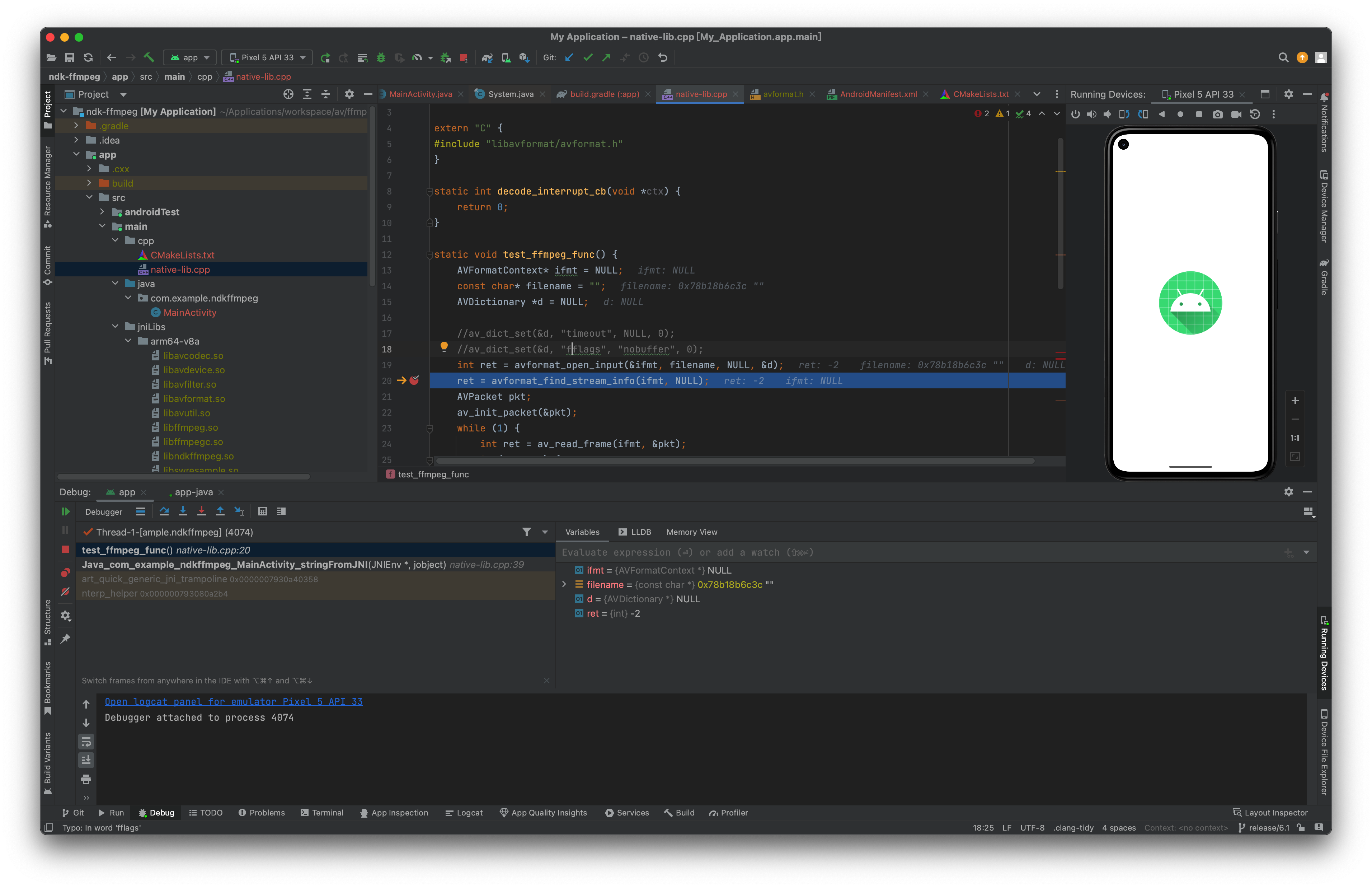
macOS上编译android的ffmpeg及ffmpeg.c
1 前言 前段时间介绍过使用xcode和qt creator编译调试ffmepg.c,运行平台是在macOS上,本文拟介绍下android平台如何用NDK编译链编译ffmepg库并使用。 macOS上使用qt creator编译调试ffmpeg.c macOS上将ffmpeg.c编译成Framework 大体思路: 其…...
RxSwift - 实现一个MVVM架构的TableView
文章目录 RxSwift - 实现一个MVVM架构的TableView前沿MVVM架构的Tableview目录结构1、模型(Model)2、视图模型(ViewModel)3、视图(View) 界面效果 RxSwift - 实现一个MVVM架构的TableView 前沿 MVVM架构在…...

在 CentOS 7 上安装并配置 Redis 允许远程连接的详细教程
第一部分:安装 Redis Redis 是一款高性能的键值存储系统,广泛应用于缓存、消息队列及数据库场景。下面是如何在 CentOS 7 系统上安装 Redis 的步骤。 步骤1:安装 EPEL 仓库 EPEL (Extra Packages for Enterprise Linux) 提供了许多 CentOS 默…...
越来越多企业选择开源批发订货系统
在当今竞争激烈的市场环境中,越来越多的企业选择开源批发订货系统来提高运营效率、降低成本并实现业务的数字化转型。以下是开源批发订货系统的四大优势及其重要功能: 首先,开源批发订货系统具有高度的灵活性和定制性。由于其源代码开放&…...
KT6368A双模蓝牙芯片上电到正常发送AT指令或指令复位需要多久
一、简介 KT6368A芯片上电到正常发送AT指令,或者开启蓝牙广播被搜索到,或者指令复位需要多久等等系列问题总结 详细描述 其实这些问题归结到一起,就还是一个问题,芯片上电需要多久的时间 在另外一份文档里面,是有描…...

代码随想录算法训练营第38天 | 509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
代码随想录算法训练营第38天 | 509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯 理论基础自己看到题目的第一想法看完代码随想录之后的想法 链接: 509. 斐波那契数 链接: 70. 爬楼梯 链接: 746. 使用最小花费爬楼梯 理论基础 五部曲: 1.确定dp数组…...

变现实谈,我要的不是灵光一现,而是真实的实现!——感悟篇
变现要的是行动不是想法 正文时代奇点奇迹 点题以己及人 正文 每当我看到了一个有趣的事情 我会在脑中构思一些想法 会贴合我当下的想要做的事情 比如 在我写下这篇文章之前 我看到了 二战期间的诞生的一个奇迹 可口可乐 我就思考 咦 原来可口可乐居然是在这么个时间点成长…...

Matlab操作Excel筛选指定数据的对应数据
Matlab中在表格中寻找指定汉字,并返回其所在行数, 将该行数的另一列提取出来。 目录 一、前言 二、直接在命令行输出 三、保存筛选数据excel 一、前言 源数据excel: 指定汉子:买,得到下面数据: 二、直接…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
