一维时间序列信号的改进小波降噪方法(MATLAB R2021B)
目前国内外对于小波分析在降噪方面的方法研究中,主要有小波分解与重构法降噪、小波阈值降噪、小波变换模极大值法降噪等三类方法。
(1)小波分解与重构法降噪
早在1988 年,Mallat提出了多分辨率分析的概念,利用小波分析的多分辨率特性进行分解。小波分解能将含噪信号分解,得到一组小波系数,然后在重构时对噪声所在频带小波系数进行舍弃,从而有效的进行信号的降噪。其文章中也给出了小波分解和重构的快速算法,称为 Mallet 算法。小波分解与重构法降噪是小波分析被应用于降噪领域最为基本的方法,也是后续一些降噪方法的基础。
(2)小波阈值降噪
小波阈值降噪的基本原理是将混合信号进行不同层次的小波分解,在每个层次利用阈值对小波系数进行处理,过滤掉噪声所在频带,然后对信号进行重构,达到降噪的目的。噪声信号一般在高频部分,所以一般对每层的高频系数进行阈值处理。
(3)小波变换模极大值降噪方法
在信号领域,信号的重要信息往往包含在其突变部分和奇异点之中,所以对于信号奇异点的检测研究至关重要。在小波变换的理论中,lip指数直接影响着模极大值和分解尺度之间的关系。通常情况下,若lip指数大于零,则该信号的模极大值随着分解尺度的增大而增大;若lip指数小于零,则该信号的模极大值随着分解分解尺度的增大而减小。通常的实测信号之中,有用信号的lip指数大于零,而噪声的lip指数小于零,这样就能对有用信号和噪声进行区分,在选出有用信号产生的模极大值点之后,利用这些有用的模极大值点对信号进行重建,就可以达到降噪的目的。
鉴于此,提出一种改进小波降噪方法,该方法提供了一种分解层数选择策略,并使用一个新公式来估计噪声阈值,运行环境为MATLAB R2021B。
%---------------------通过计算peak-to-sum ratio来确定分解层数----------------
%变量初始化
Sj = [1:14]; %每层的peak-to-sum值
Tr = 0.5; %稀疏性判定指标,可调超参数
k = 0; %分解层数%循环遍历所有的细节系数
for level = 1 : 1 : 14%分解到第j层时的细节系数向量wj = cell2mat(cD(level)); %分为L(负数)与H(正数)两组wj_L = []; %负系数数组wj_H = []; %正系数数组for index = 1 : 1 : length(wj)if wj(index) <= 0wj_L = cat(1, wj_L, wj(index));elsewj_H = cat(1, wj_H, wj(index));endend%分别用元胞数组记录cD_L{level, 1} = wj_L; cD_H{level, 1} = wj_H; %计算peak-to-sum值,裁定第j的稀疏性maxwj = max(abs(wj)); %第j层最大的细节系数sumwj = sum(abs(wj)); %第j层细节系数绝对值之和Sj(level) = maxwj / sumwj;完整代码:https://mbd.pub/o/bread/mbd-ZpWWm59wend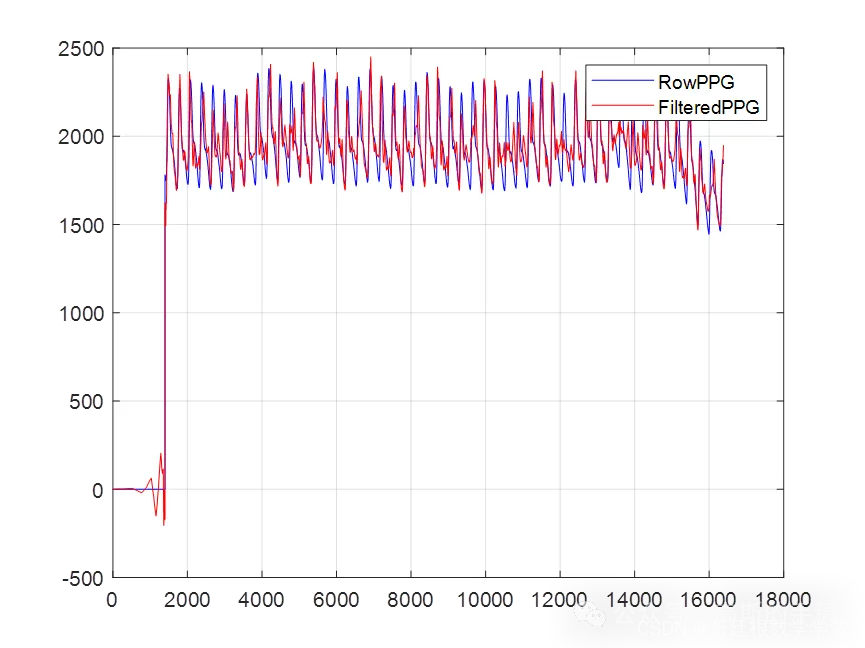
相关文章:

一维时间序列信号的改进小波降噪方法(MATLAB R2021B)
目前国内外对于小波分析在降噪方面的方法研究中,主要有小波分解与重构法降噪、小波阈值降噪、小波变换模极大值法降噪等三类方法。 (1)小波分解与重构法降噪 早在1988 年,Mallat提出了多分辨率分析的概念,利用小波分析的多分辨率特性进行分…...
Java整合EasyExcel实战——3(上下列相同合并单元格策略)
参考:https://juejin.cn/post/7322156759443095561?searchId202405262043517631094B7CCB463FDA06https://juejin.cn/post/7322156759443095561?searchId202405262043517631094B7CCB463FDA06 准备条件 依赖 <dependency><groupId>com.alibaba</gr…...
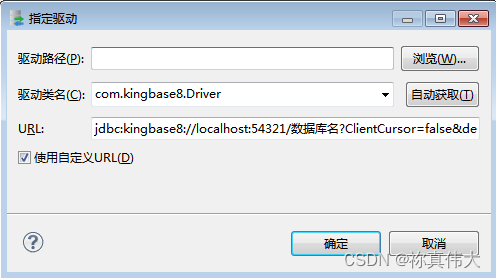
dmdts连接kingbase8报错
dmdts连接kingbase报错 环境介绍1 人大金仓jdbc配置2 dmdts 人大金仓jdbc默认配置3 dmdts 修改jdbc配置4 达梦产品学习使用列表 环境介绍 dts版本 使用dmdts连接kingbase金仓数据库报错 无效的URL 对比jdbc连接串,修改配置解决 1 人大金仓jdbc配置 配置URL模版信息等 类名…...

【算法训练 day44 分割等和子集】
目录 一、分割等和子集-LeetCode 416思路实现代码1.二维dp代码2.一维dp代码 问题总结 一、分割等和子集-LeetCode 416 Leecode链接: leetcode 416 文章链接: 代码随想录 视频链接: B站 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集&…...
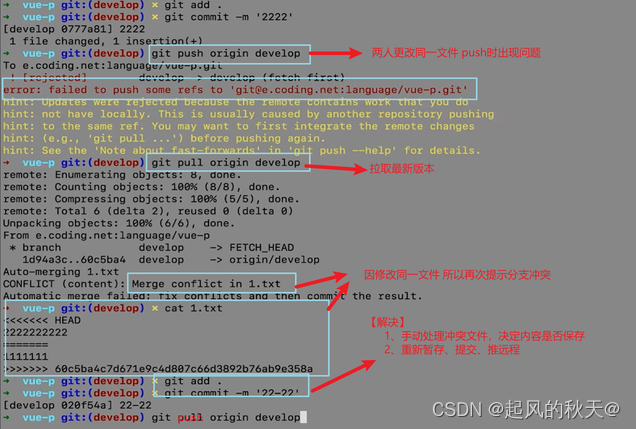
前端实习记录——git篇(一些问题与相关命令)
1、版本控制 (1)版本回滚 git log // 查看版本git reset --mixed HEAD^ // 回滚到修改状态,文件内容没有变化git reset --soft HEAD^ // 回滚暂存区,^的个数代表几个版本git reset --hard HEAD^ // 回滚到修改状态ÿ…...

XML Web 服务技术解析:WSDL 与 SOAP 原理、应用案例一览
XML Web服务是一种用于在网络上发布、发现和使用应用程序组件的技术。它基于一系列标准和协议,如WSDL、SOAP、RDF和RSS。下面是一些相关的内容: WSDL(Web服务描述语言):用于描述Web服务的基于XML的语言,定义…...

解析Java中1000个常用类:FunctionalInterface类,你学会了吗?
Java 8 引入了一系列新的特性和改进,其中之一便是函数式编程。函数式接口(Functional Interface)是函数式编程的核心概念之一。本文将深入探讨 FunctionalInterface 注解,介绍其用法、重要性,并通过示例展示如何在实际开发中应用函数式接口。 什么是函数式接口? 函数式…...

Kafka自定义分区器编写教程
1.创建java类MyPartitioner并实现Partitioner接口 点击灯泡选择实现方法,导入需要实现的抽象方法 2.实现方法 3.自定义分区器的使用 在自定义生产者消息发送时,属性配置上加入自定义分区器 properties.put(ProducerConfig.PARTITIONER_CLASS_CONFIG,&q…...

python移动文件
测试1(直接把B文件夹移动到了A里,成为了A的子文件夹) import os import shutil# 移动文件夹,B文件夹在当前目录没有了,跑到了A的子文件里 ## shutil.move(./example1/B/, ./example1/A/)测试2(B文件不动,将B文件里的所有的子文件夹移动到A内…...
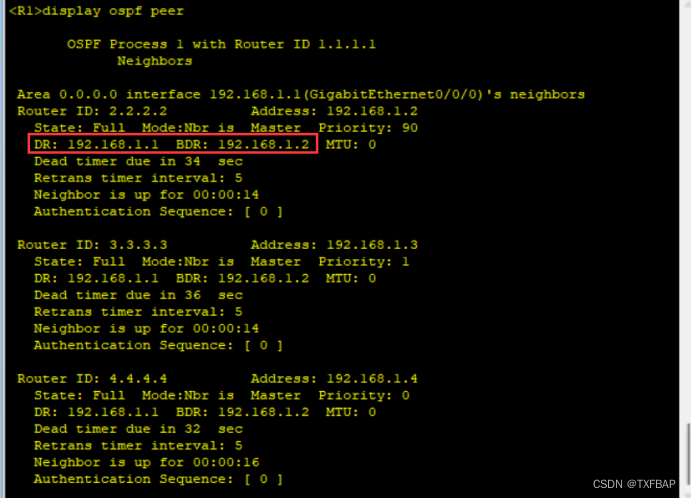
eNSP学习——OSPF的DR与BDR
目录 相关命令 原理概述 实验内容 实验目的 实验拓扑 实验编址 实验步骤 1、基本配置 2、搭建基本的OSPF网络 3、查看默认情况下的DR/BDR状态 4、根据现网需求影响DR/BDR选举 相关命令 [R4]int g0/0/0 [R4-GigabitEthernet0/0/0]ospf network-type p2mp //在接…...
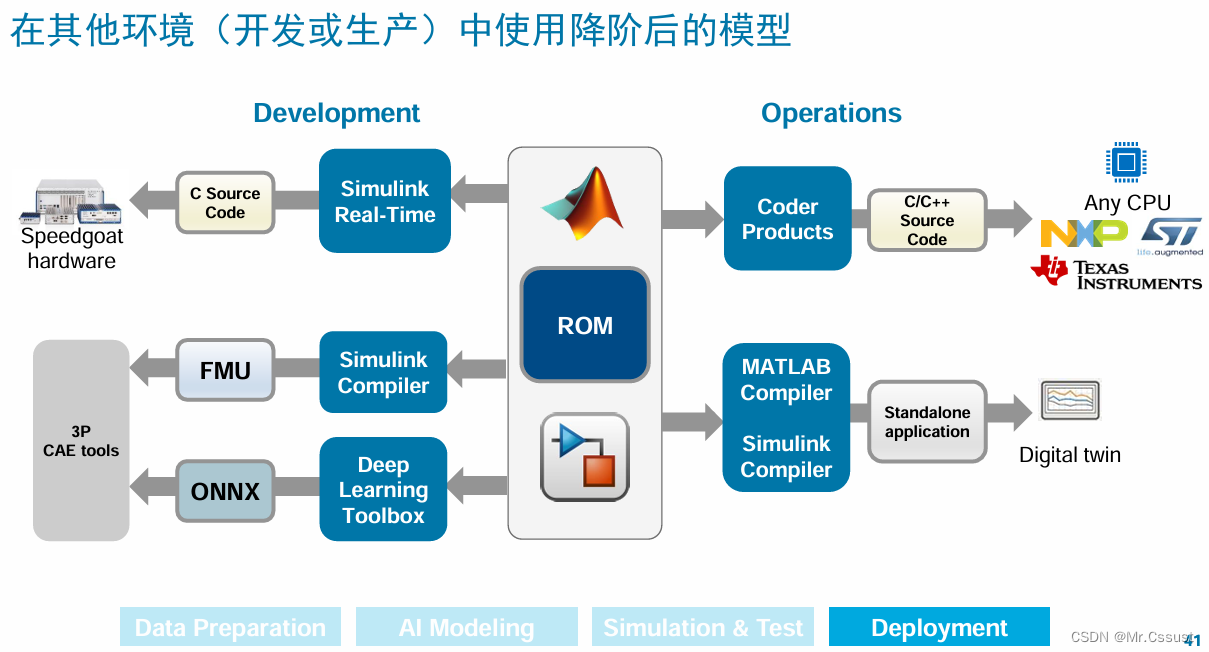
【文献阅读】应用人工智能在Simulink中开发软件
参考文献:《AI用于Simulink模型的降阶方法和应用场景》Mathworks在2024年MATLAB XEPO大会的演讲 文章目录: 1、模型框架 2、数据准备 3、AI建模 4、仿真和测试 5、部署应用 Tips:降阶模型(Reduced Order Modeling࿰…...

【计算机毕设】基于SpringBoot的房产销售系统设计与实现 - 源码免费(私信领取)
免费领取源码 | 项目完整可运行 | v:chengn7890 诚招源码校园代理! 1. 研究目的 随着房地产市场的发展和互联网技术的进步,传统的房产销售模式逐渐向线上转移。设计并实现一个基于Spring Boot的房产销售系统࿰…...
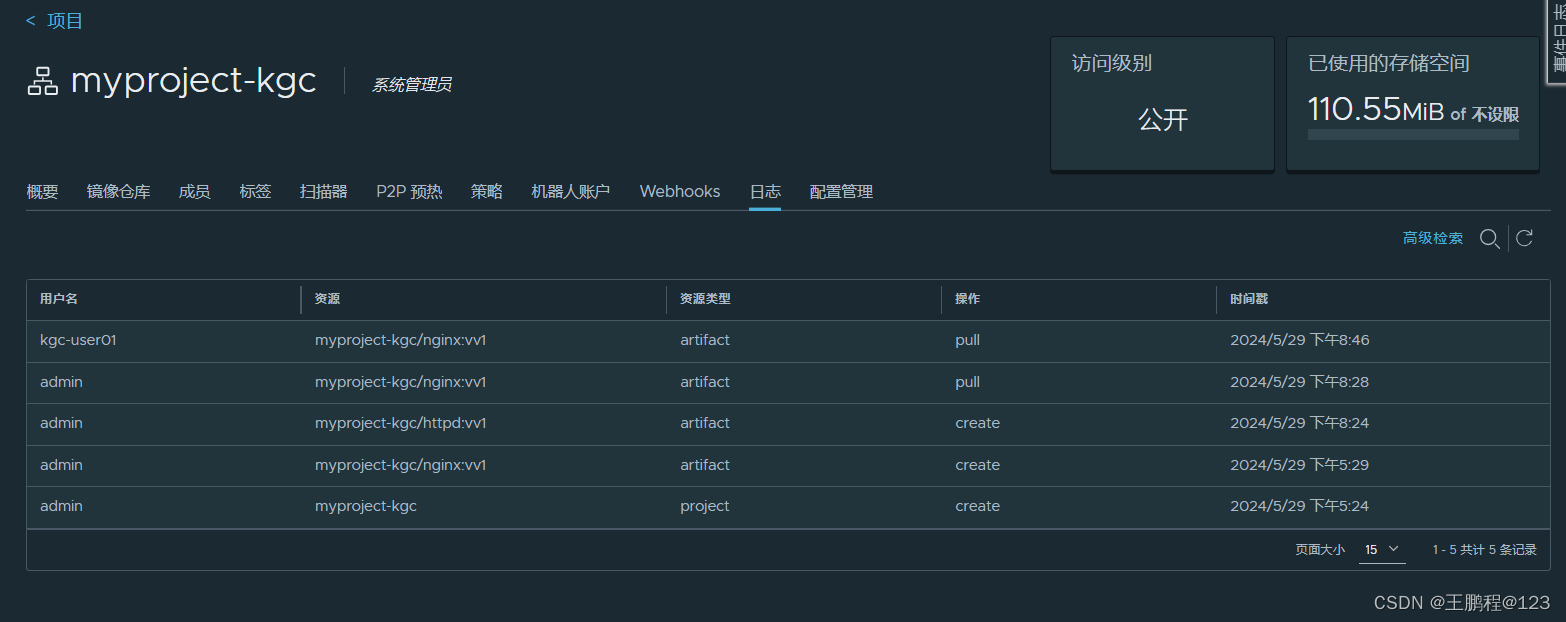
Docker 私有仓库部署和管理
目录 一、案例一 概述 二、案例一 前置知识点 2.1、什么是 Docker Compose 2.2、什么是 Consul 三、案例一 使用 docker Compose 搭建 Consul 集群环境 3.1、案例实验环境 3.2、案例需求 四、案例实施 4.1、Docker 网络通信 1)端口映射 2…...
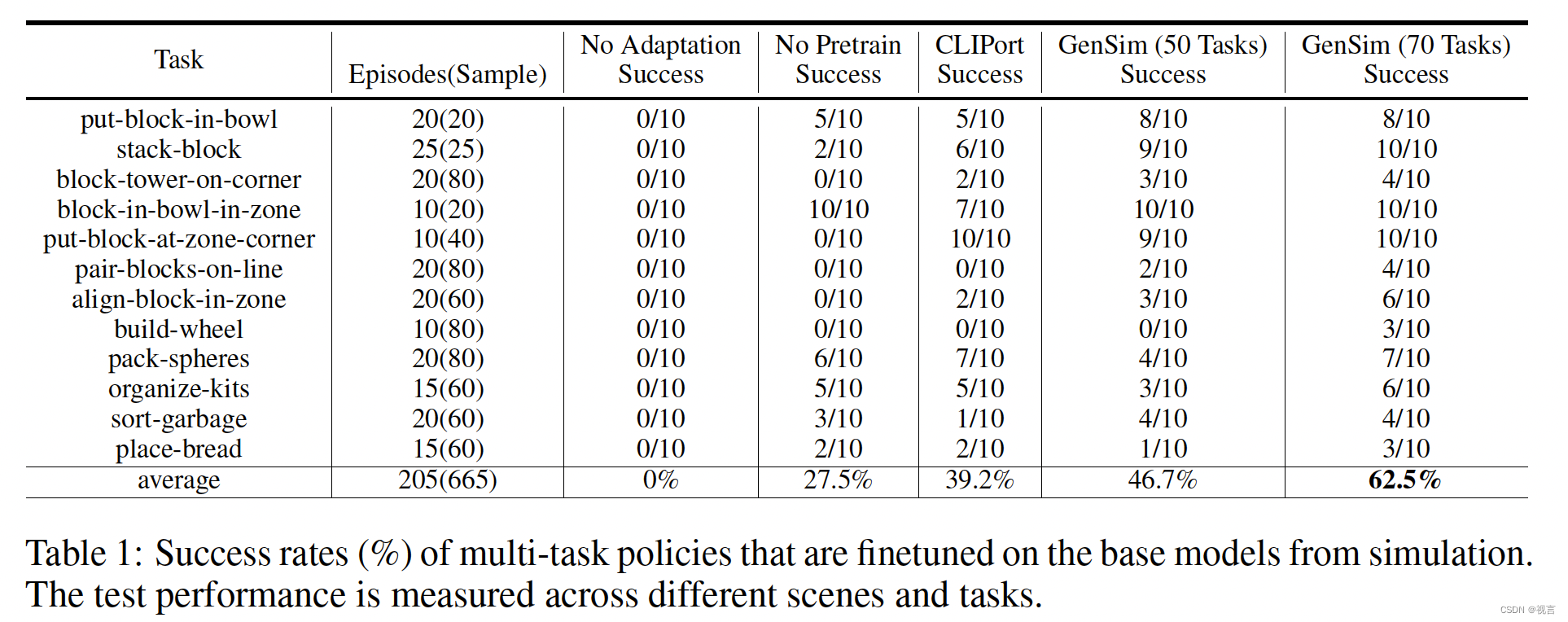
大模型时代的具身智能系列专题(六)
UCSD 王小龙组 王小龙是UCSD电子与计算机工程系的助理教授。他曾在加州大学伯克利分校与Alexei Efros和Trevor Darrell一起担任博士后研究员,在CMU RI获得了机器人学博士学位,师从Abhinav Gupta。他的研究重点是通过视频和物理机器人交互数据来学习3D和…...
Pytorch入门需要达到的效果
会搭建深度学习环境和依赖包安装 使用Anaconda创建环境、在pytorch官网安装pytorch、安装依赖包 会使用常见操作,例如matmul,sigmoid,softmax,relu,linear matmul操作见文章torch.matmul()的用法 sigmoid࿰…...
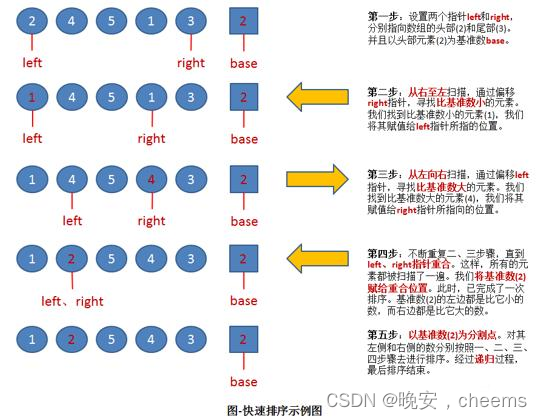
数据结构的快速排序(c语言版)
一.快速排序的概念 1.快排的基本概念 快速排序是一种常用的排序算法,它是基于分治策略的一种高效排序算法。它的基本思想如下: 从数列中挑出一个元素作为基准(pivot)。将所有小于基准值的元素放在基准前面,所有大于基准值的元素放在基准后面。这个过程称为分区(partition)操作…...
)
数据结构基础篇(4)
十六.循环链表 概念 循环链表是一种头尾相接的链表(最后一个结点的指针域指向头结点,整个链表形成一个环)优点 从表任一结点出发均可找到表中其他结点判断终止 由于循环链表中没有NULL指针,所以涉及遍历操作时,终止条…...
使用cad绘制一个螺旋输送机
1、第一步,绘制一个矩形 2、使用绘图中的样条线拟合曲线,绘制螺旋线。 绘制时使用上下辅助线、阵列工具绘制多个竖线保证样条线顶点在同一高度。 3、调整矩形右侧的两个顶点,使其变形。 矩形1和矩形2连接时,使用blend命令&#…...

迭代器模式(行为型)
目录 一、前言 二、迭代器模式 三、总结 一、前言 迭代器模式(Iterator Pattern)是一种行为型设计模式,提供一种方法顺序访问一个聚合对象中各个元素,而又不暴露该对象的内部表示。总的来说就是分离了集合对象的遍历行为,抽象出…...
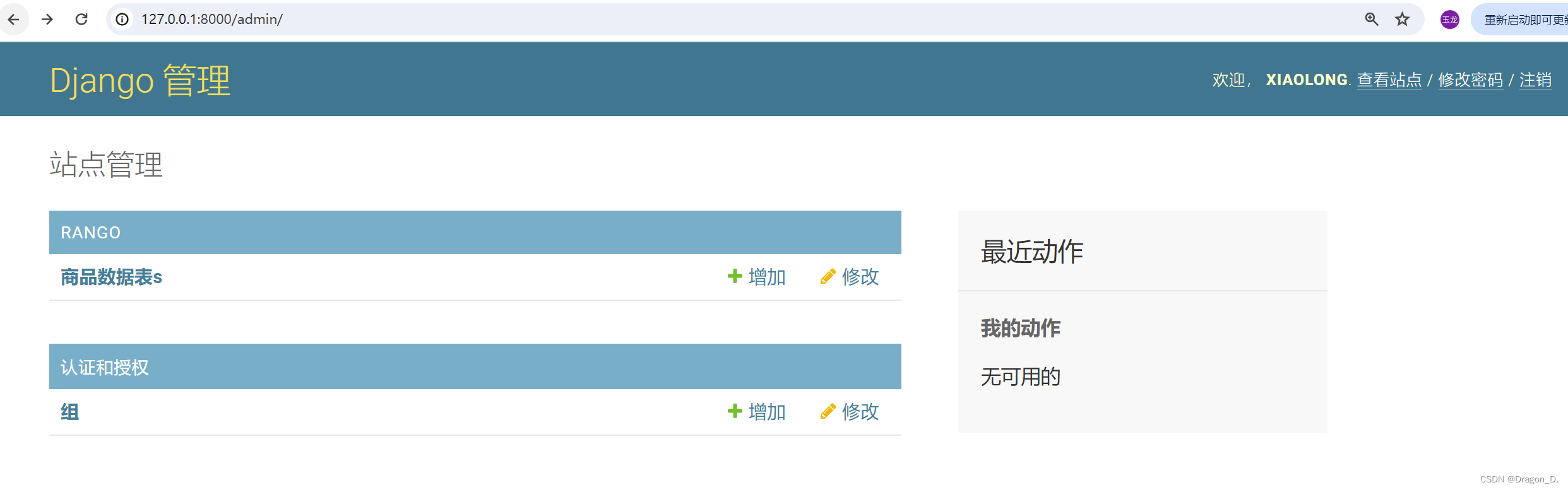
Django——Admin站点(Python)
#前言: 该博客为小编Django基础知识操作博客的最后一篇,主要讲解了关于Admin站点的一些基本操作,小编会继续尽力更新一些优质文章,同时欢迎大家点赞和收藏,也欢迎大家关注等待后续文章。 一、简介: Djan…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...
