当前位置： 首页 > news >正文

Window系统安装Docker

news 2025/12/16 1:28:46

        因为docker只适合在liunx系统上运行，如果在window上安装的话，就需要开启window的虚拟化，打开控制面板，点击程序，在程序和功能中可以看到启动和关闭window功能，点开后，找到Hyper-V，Window虚拟机监控程序平台，适用于liunx的window子系统，虚拟机平台，这四个。然后勾选点击确定，全部打开后会要求重启系统，等待重启结束

然后打开docker官网，选择上面的Products下选择Docker Desktop，意思是下载桌面版本的Docker，

 

 然后选择Download for Windows，下载windows版本的Docker

下载后得到一个exe文件，双击安装运行，中途如果让安装东西就确定，然后next，直到安装完成

安装完成后双击打开docker Desktop，点击接受，

Docker会提示需要登录，可以去docker官网创建账号登录，也可以点击下方的Continue without signing in（不登录继续）

 如果登录会提示选择角色，这个根据自己选一个就可以

然后没有问题的话就可以进入到docker主页面了

 如果遇到相关报错，可以尝试升级下wsl --update

至此在window上安装docker就完成了

相关文章：

Window系统安装Docker

因为docker只适合在liunx系统上运行，如果在window上安装的话，就需要开启window的虚拟化，打开控制面板，点击程序，在程序和功能中可以看到启动和关闭window功能，点开后，找到Hyper-V，Wi…...

编程日记 2024/6/1 5:39:41

RabbitMQ不完整的笔记

同步的不足 1、拓展性差，当要添加功能时，需要在原来的功能代码上做修改，高耦合。 2、性能下降，调用者需要等待服务提供者执行完返回结果后，才能继续向下执行 3、级联失败，由于我们是基于OpenFeign调用交易…...

编程日记 2024/6/1 5:37:38

微软Edge浏览器深度解析：功能、同步、隐私与安全

微软Edge浏览器是微软公司开发的一款网页浏览器，它基于Chromium内核，提供了快速、安全和兼容性良好的网页浏览体验。以下是关于微软Edge浏览器的详细信息和使用指南： 微软Edge浏览器的主要特点： 1. 基于Chromium内核： 渲染引擎：Chromium内核是基于开源项目Blink的，它…...

编程日记 2024/6/1 5:34:35

网络性能测试工具：iperf3介绍

文章目录 前言一、iperf3 的安装和使用下载和安装参数说明 二、iperf3 测试服务端启动客户端启动服务端输出反向测试客户端服务端 前言 新接触的网络环境如何评估网络带宽和吞吐量呢，有的项目没有对业务流量进行合理规划，服务或者中间件出口带宽经常有被…...

编程日记 2024/6/1 5:33:34

scp：Linux系统本地与远程文件传输命令

scp 是Linux系统中用于在本地主机和远程主机之间进行文件传输的命令。 详细说明： scp 命令用于安全地将文件从一个主机传输到另一个主机，所有传输数据都是加密的。语法： scp [参数] [源文件路径] [目标主机:目标路径] 参数说明&#xff1a…...

编程日记 2024/6/1 5:32:33

python基础（习题、资料）

免费提取资料： 练习、资料免费提取。持续更新迅雷云盘https://pan.xunlei.com/s/VNz6kH1EXQtK8j-wwwz_c0k8A1?pwdrj2x# 本文为Python的进阶知识合辑，包括列表（List）、元组（Tuple）、字典（Dic…...

编程日记 2024/6/1 5:29:31

shell脚本免交互

shell脚本的编写一方面为了减少我们命令的输入，另一方面也可以进行简单的自动化运行，其中为了实现自动化过程，一个很重要的点就是免交互，本篇文章跟大家简单分享两个常用的免交互的方法。 Here Document Here document 通过内联重…...

编程日记 2024/6/1 5:28:29

WPF学习笔记：给文字添加线性渐变效果

<TextBox Text"XXX信息管理系统" VerticalAlignment"Center" Background"Transparent" HorizontalAlignment"Center" FontSize"35" FontWeight"Normal"> <TextBox.Effect> <…...

编程日记 2024/6/1 5:27:28

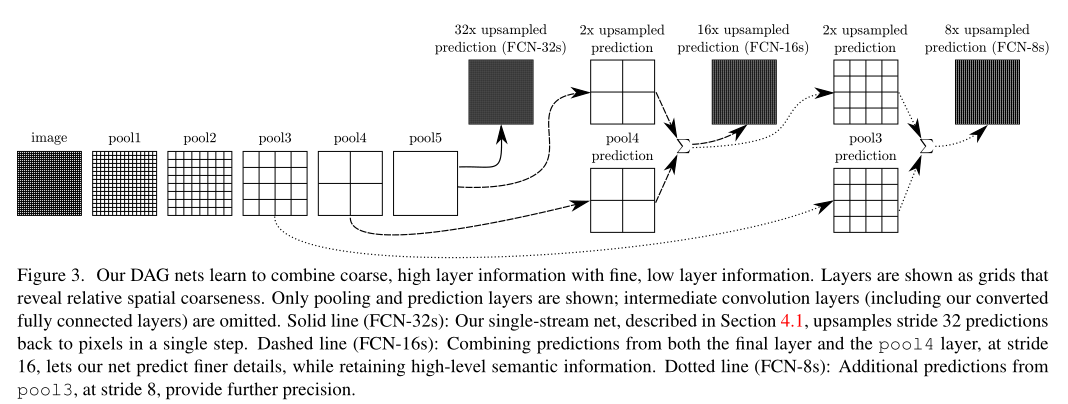
Fully Convolutional Networks for Semantic Segmentation--论文笔记

论文笔记 资料 1.代码地址 2.论文地址 https://arxiv.org/abs/1411.4038 3.数据集地址 论文摘要的翻译 卷积网络是强大的视觉模型&#xff0c;可以产生特征层次结构。我们表明&#xff0c;卷积网络本身&#xff0c;经过端到端&#xff0c;像素对像素的训练&#xff0c;在…...

编程日记 2024/6/1 5:26:27

Camworks编程怎么样：深度解析其四大特点、五大应用领域、六大优势与七大挑战

Camworks编程怎么样&#xff1a;深度解析其四大特点、五大应用领域、六大优势与七大挑战 Camworks编程&#xff0c;作为计算机辅助制造&#xff08;CAM&#xff09;领域的一款重要软件&#xff0c;近年来在制造业中得到了广泛的应用。那么&#xff0c;Camworks编程究竟怎么样呢…...

编程日记 2024/6/1 5:24:24

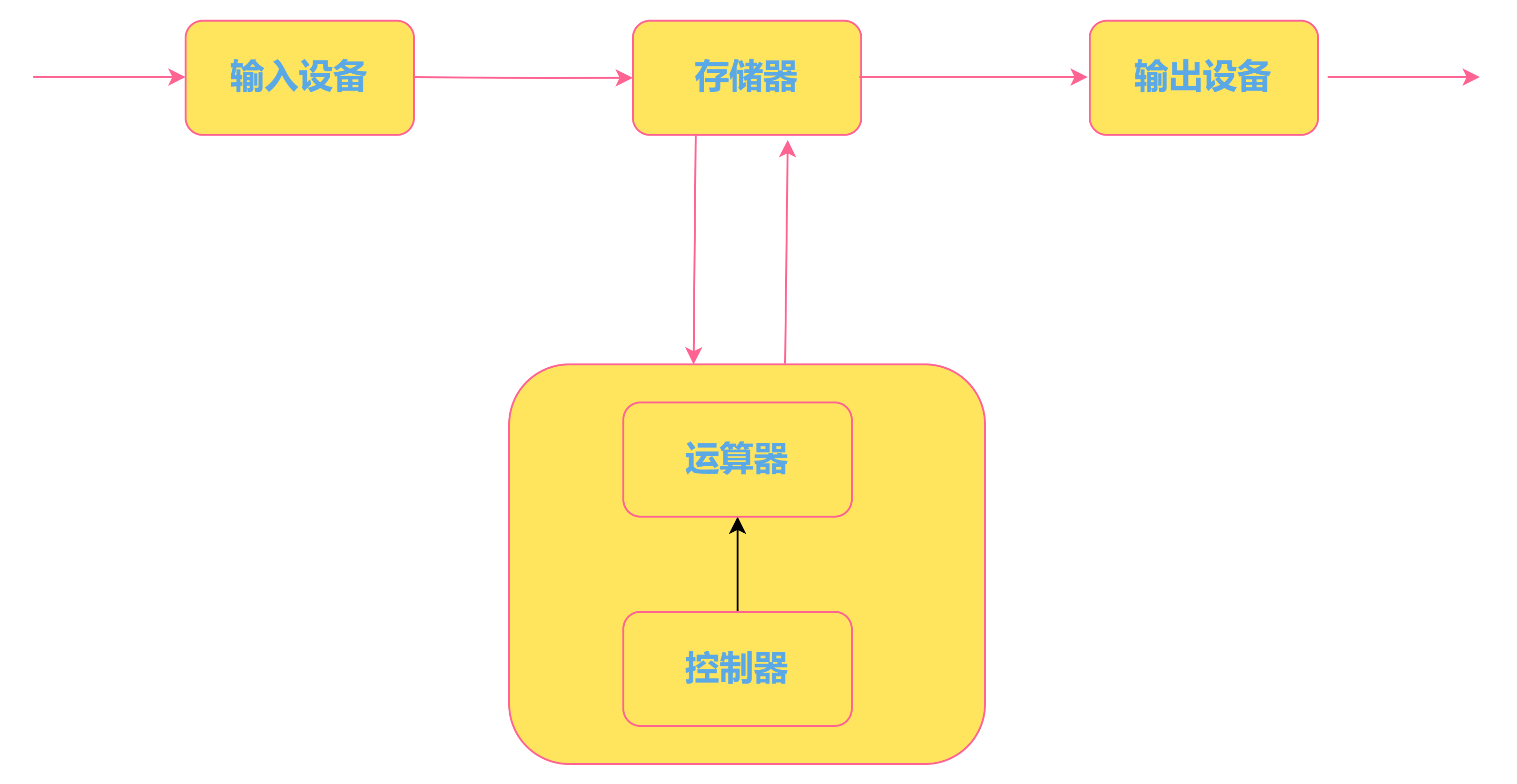
【Linux】操作系统之冯诺依曼体系

&#x1f389;博主首页&#xff1a; 有趣的中国人 &#x1f389;专栏首页&#xff1a; Linux &#x1f389;其它专栏&#xff1a; C初阶 | C进阶 | 初阶数据结构 小伙伴们大家好&#xff0c;本片文章将会讲解 操作系统中 冯诺依曼体系 的相关内容。 如果看到最后您觉得这篇文…...

编程日记 2024/6/1 5:23:22

c++ QT 实现QMediaPlayer播放音频显示音频级别指示器

文章目录 效果图概述代码总结 效果图 概述 QMediaPlayer就不介绍了&#xff0c;就提供了一个用于播放音频和视频的媒体播放器 QAudioProbe 它提供了一个探针&#xff0c;用于监控音频流。当音频流被捕获或播放时&#xff0c;QAudioProbe 可以接收到音频数据。这个类在需要访问…...

编程日记 2024/6/1 5:21:20

失之毫厘差之千里之load和loads

起源 最近在读pandas库的一些文档的时候&#xff0c;顺便也会将文档上的一些demo在编辑器中进行运行测试&#xff0c;其中在读到pandas处理Json数据这一节的时候&#xff0c;我还是像往常一样&#xff0c;将文档提供的demo写一遍&#xff0c;结果在运行的时候&#xff0c;直接…...

编程日记 2024/6/1 5:20:19

element ui在移动端的适配问题

element ui在移动端的适配问题 问题1&#xff1a; 给el-table表头添加背景色&#xff0c;使用以下代码 :header-row-style“{ background: ‘linear-gradient(90deg, #0079FA 0%, #00C7DD 100%)’ }” 在安卓手机上显示正常&#xff0c;在ios手机上显示背景色添加到每一个th中…...

编程日记 2024/6/1 5:19:18

堆排序详细理解

目录 一、前备知识 二、建堆 2.2.1 向上调整算法建堆 2.2.2 向下调整算法建堆 三、排序 3.1 常见问题 3.2 思路 3.3 源码 一、前备知识 详细图解请点击&#xff1a;二叉树的顺序实现-堆-CSDN博客 本文只附上向上/向下调整算法的源码 //交换 void Swap(int* p, int* …...

编程日记 2024/6/1 5:18:17

RK3588+FPGA+AI高性能边缘计算盒子，应用于视频分析、图像视觉等

搭载RK3588&#xff08;四核 A76四核 A55&#xff09;&#xff0c;CPU主频高达 2.4GHz &#xff0c;提供1MB L2 Cache 和 3MB L3 &#xff0c;Cache提供更强的 CPU运算能力&#xff0c;具备6T AI算力&#xff0c;可扩展至38T算力。 产品规格 系统主控CPURK3588&#xff0c;四核…...

编程日记 2024/6/1 5:15:14

07-操作元素（键盘和鼠标事件）

在前面的文章中重点介绍了一些元素的定位方法&#xff0c;定位到元素后&#xff0c;就需要操作元素了。本篇总结了web页面常用的一些操作元素方法&#xff0c;可以统称为行为事件。 一、简单操作 点击按钮&#xff08;鼠标左键&#xff09;&#xff1a;click()清空输入框&…...

编程日记 2024/6/1 5:14:13

3389，为了保障3389端口的安全，我们可以采取的措施

3389端口&#xff0c;作为远程桌面协议&#xff08;RDP&#xff09;的默认端口&#xff0c;广泛应用于Windows操作系统中&#xff0c;以实现远程管理和控制功能。然而&#xff0c;正因为其广泛使用&#xff0c;3389端口也成为许多潜在安全威胁的入口。因此&#xff0c;确保3389…...

编程日记 2024/6/1 5:11:09

Java集合【超详细】2 -- Map、可变参数、Collections类

文章目录 一、Map集合1.1 Map集合概述和特点【理解】1.2 Map集合的基本功能【应用】1.3 Map集合的获取功能【应用】1.4 Map集合的两种遍历方式 二、HashMap集合2.1 HashMap集合概述和特点【理解】2.2 HashMap的组成、构造函数2.3 put、查找方法2.4 HashMap集合应用案例【应用】…...

编程日记 2024/6/1 5:10:08

最佳 Mac 数据恢复：恢复 Mac 上已删除的文件

尝试过许多 Mac 数据恢复工具&#xff0c;但发现没有一款能达到宣传的效果&#xff1f;我们重点介绍最好的 Mac 数据恢复软件 没有 Mac 用户愿意担心数据丢失&#xff0c;但您永远不知道什么时候会发生这种情况。无论是意外删除 Mac 上的重要文件、不小心弄湿了 Mac、感染病毒…...

编程日记 2024/6/1 5:08:07

wordpress后台更新后 前端没变化的解决方法

使用siteground主机的wordpress网站&#xff0c;会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后&#xff0c;网站没有变化的情况。 不熟悉siteground主机的新手&#xff0c;遇到这个问题&#xff0c;就很抓狂&#xff0c;明明是哪都没操作错误&#x…...

编程新知 2025/12/15 5:20:00

springboot 百货中心供应链管理系统小程序

一、前言 随着我国经济迅速发展&#xff0c;人们对手机的需求越来越大&#xff0c;各种手机软件也都在被广泛应用&#xff0c;但是对于手机进行数据信息管理&#xff0c;对于手机的各种软件也是备受用户的喜爱&#xff0c;百货中心供应链管理系统被用户普遍使用&#xff0c;为方…...

编程新知 2025/12/10 15:27:46

基于FPGA的PID算法学习———实现PID比例控制算法

基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容&#xff1a;参考网站&#xff1a; PID算法控制 PID即&#xff1a;Proportional&#xff08;比例&#xff09;、Integral&#xff08;积分&…...

编程新知 2025/12/13 22:32:24

UE5 学习系列（三）创建和移动物体

这篇博客是该系列的第三篇&#xff0c;是在之前两篇博客的基础上展开&#xff0c;主要介绍如何在操作界面中创建和拖动物体&#xff0c;这篇博客跟随的视频链接如下&#xff1a; B 站视频&#xff1a;s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

编程新知 2025/12/9 0:41:46

智能在线客服平台：数字化时代企业连接用户的 AI 中枢

随着互联网技术的飞速发展&#xff0c;消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁&#xff0c;不仅优化了客户体验&#xff0c;还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用&#xff0c;并…...

编程新知 2025/12/14 22:40:49

优选算法第十二讲：队列 + 宽搜 优先级队列

优选算法第十二讲&#xff1a;队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

编程新知 2025/12/15 22:17:46

在Ubuntu24上采用Wine打开SourceInsight

1. 安装wine sudo apt install wine 2. 安装32位库支持，SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库（解决显示问题） sudo apt install fonts-wqy…...

编程新知 2025/10/14 0:47:25

【分享】推荐一些办公小工具

1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由&#xff1a;大部分的转换软件需要收费&#xff0c;要么功能不齐全&#xff0c;而开会员又用不了几次浪费钱&#xff0c;借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

编程新知 2025/12/9 1:25:37

解读《网络安全法》最新修订，把握网络安全新趋势

《网络安全法》自2017年施行以来&#xff0c;在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂&#xff0c;网络攻击、数据泄露等事件频发&#xff0c;现行法律已难以完全适应新的风险挑战。 2025年3月28日&#xff0c;国家网信办会同相关部门起草了《网络安全…...

编程新知 2025/12/14 0:28:04

基于单片机的宠物屋智能系统设计与实现（论文+源码）

本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢&#xff0c;连接红外测温传感器&#xff0c;可实时精准捕捉宠物体温变化&#xff0c;以便及时发现健康异常&#xff1b;水位检测传感器时刻监测饮用水余量&#xff0c;防止宠物…...

编程新知 2025/12/9 5:10:14