纯C++做多项式拟合
一、多项式拟合用途
当前有一组对应的x、y数据,希望通过这些数据点做出近似的多项式曲线:Y=···+nX^2+mX+c
其中多项式最高次数可调,返回各个参数及曲线的拟合度R^2
二、函数实现
参数中的order为设置的多项式最高次次数,coefficients为各次的系数
double polynomialFit(vector<double>& x, vector<double>& y, unsigned char order, vector<double>& coefficients){if (x.size() <= order || y.size() <= order) {return 0;}// 构建矩阵A和向量bint m = x.size();int n = order + 1;vector<vector<double>> A(n, vector<double>(n, 0));vector<double> b(n, 0);for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {for (int k = 0; k < m; k++) {A[i][j] += pow(x[k], i+j);}}for (int k = 0; k < m; k++) {b[i] += y[k] * pow(x[k], i);}}n = A.size();for (int i = 0; i < n; i++) {// 列主元素消去int maxRow = i;double maxVal = fabs(A[i][i]);for (int k = i + 1; k < n; k++) {if (fabs(A[k][i]) > maxVal) {maxVal = fabs(A[k][i]);maxRow = k;}}if (maxRow != i) {std::swap(A[i], A[maxRow]);std::swap(b[i], b[maxRow]);}// 消元过程for (int k = i + 1; k < n; k++) {double factor = A[k][i] / A[i][i];for (int j = i; j < n; j++) {A[k][j] -= factor * A[i][j];}b[k] -= factor * b[i];}}// 回代求解vector<double> result(n, 0);for (int i = n - 1; i >= 0; i--) {double temp = b[i];for (int j = i + 1; j < n; j++) {temp -= A[i][j] * result[j];}result[i] = temp / A[i][i];}coefficients = result;double SSR=0;double SST=0;double sumY = std::accumulate(std::begin(y),std::end(y),0.0);double avgY = sumY/y.size();for(uint16_t i=0;i<y.size();i++){double actY=0;for(unsigned char j=0;j<=order;j++){actY+=pow(x[i],j)*result[j];}SSR += pow(actY-y[i],2);SST += pow(y[i]-avgY,2);}double R = 1-SSR/SST;return R;
}
三、函数调用
vector<double> xs{0,0,0,0};
vector<double> selectX;
vector<double> selectY;
selectX.push_back(..);
...
selectY.push_back(..);
...
double R = polynomialFit(selectX,selectY,3,xs);
相关文章:

纯C++做多项式拟合
一、多项式拟合用途 当前有一组对应的x、y数据,希望通过这些数据点做出近似的多项式曲线:YnX^2mXc 其中多项式最高次数可调,返回各个参数及曲线的拟合度R^2 二、函数实现 参数中的order为设置的多项式最高次次数,coefficients为…...
vulnhub靶场之FunBox-9
一.环境搭建 1.靶场描述 Its a box for beginners, but not easy. Gather careful !!! Hint: Dont waste your time ! Every BruteForce-Attack at all ports can be stopped after 1500 trys per account. Enjoy the game and WYSIWYG ! This works better with VirtualBox…...

C# 变量与参数详解
在C#编程中,变量和参数是构建程序逻辑的基础。本篇博客将深入探讨C#中的变量作用域、参数传递方式、以及一些高级特性,如in、ref、out参数,params修饰符,可选参数和命名参数等。 变量作用域 在C#中,变量的作用域分为…...
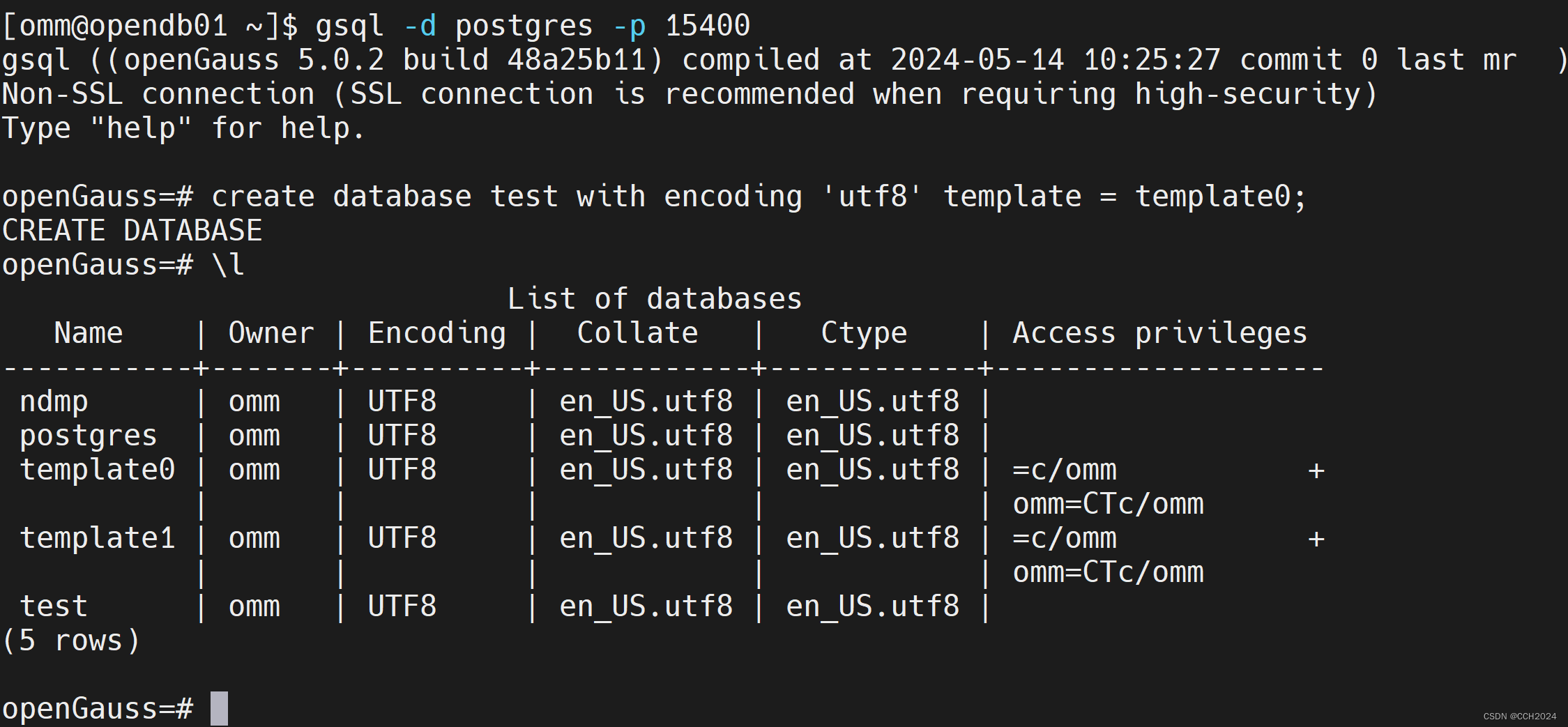
CentOS7.9部署安装OpenGauss 5.0.2企业版
1、更新系统: yum update -y 2、更改主机名: hostnamectl set-hostname opendb01 3、关闭透明页: echo never > /sys/kernel/mm/transparent_hugepage/enabled echo never > /sys/kernel/mm/transparent_hugepage/defrag# 加入开机自启动 echo …...

java基础-chapter15(io流)
io流:存储和读取数据的解决方案 I:input O:output io流的作用:用于读写数据(本地文件,网络) io流按照流向可以分为: 输出流:程序->文件 输入流:文件->程序 io流按照操作文件…...

mysql去除重复数据
需求描述 doc表有很多重复的title,想去除掉重复的记录 表结构 CREATE TABLE doc (id INT PRIMARY KEY,title VARCHAR(255),content TEXT );去重SQL -- 创建临时表 CREATE TEMPORARY TABLE temp_doc AS SELECT * FROM doc WHERE 10;-- 插入唯一的记录(每个title最…...
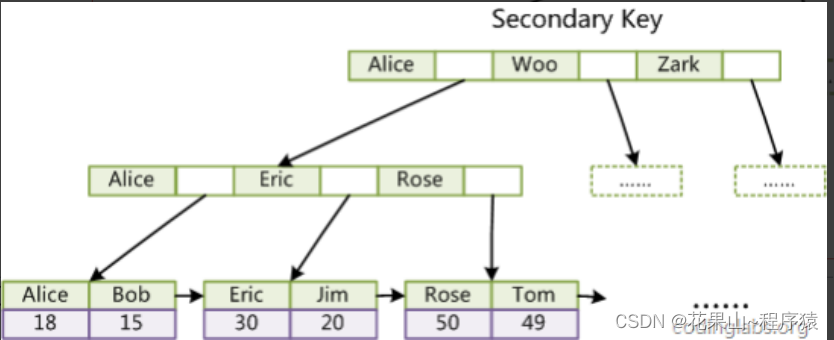
MySQL基础索引知识【索引创建删除 | MyISAM InnoDB引擎原理认识】
博客主页:花果山~程序猿-CSDN博客 文章分栏:MySQL之旅_花果山~程序猿的博客-CSDN博客 关注我一起学习,一起进步,一起探索编程的无限可能吧!让我们一起努力,一起成长! 目录 一,索引用…...

SJ601-II垂直法阻燃性能测试仪
一、主要用途 主要用于有阻燃要求的纺织品如机织物、针织物、涂层产品、层压产品、服装织物、装饰织物、帐篷织物、窗帘幕布、建材装饰织物等材料阻燃性能的测定。并用于窗帘幕布阻燃等级的测定和防火封堵材料的型式过证。 二、仪器特征 1、脉冲自动点火,安全可靠…...
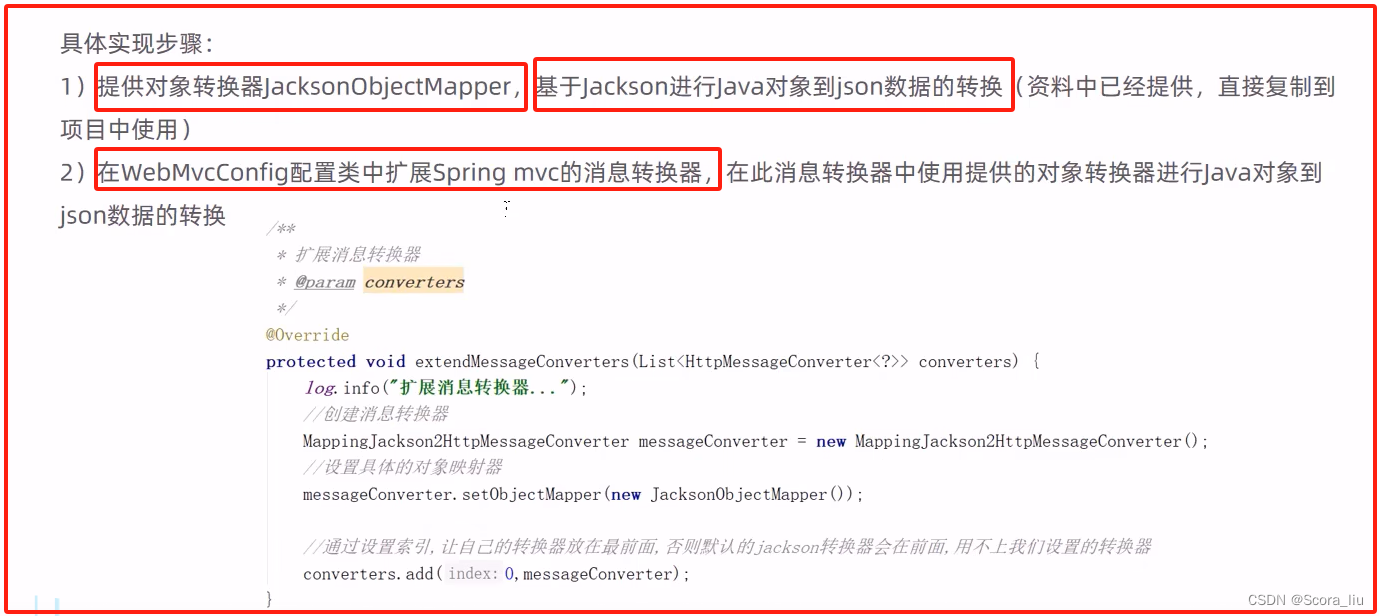
瑞吉外卖项目学习笔记(二)后台系统的员工管理业务开发
一、完善登录功能 1.1 问题分析 1.2 代码实现 package com.itheima.reggie.filter;//这是一个过滤器类 //登录检查过滤器import com.alibaba.fastjson.JSON; import com.itheima.reggie.common.R; import lombok.extern.slf4j.Slf4j; import org.slf4j.Logger; import org.slf…...

Unity OutLine 模型外描边效果
效果展示: 下载链接...
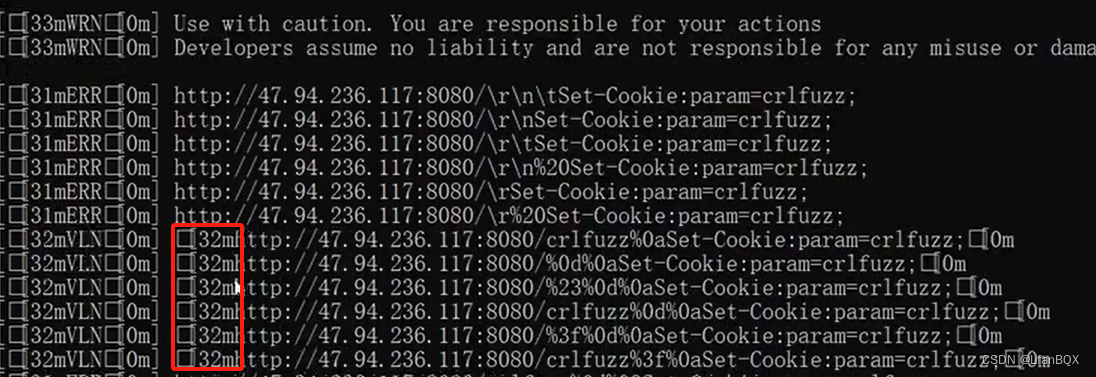
CRLF注入漏洞
1.CRLF注入漏洞原理 Nginx会将 $uri进行解码,导致传入%0a%0d即可引入换行符,造成CRLF注入漏洞。 执行xss语句 2.漏洞扩展 CRLF 指的是回车符(CR,ASCII 13,\r,%0d) 和换行符(LF,ASCII 10,\n&am…...

理解接口回调及其在 RabbitMQ 中的实际运用
介绍 接口回调是一种常见的编程模式,它在异步编程中发挥着重要作用。本文将通过一个简单的示例介绍接口回调的概念和原理,并探讨它在 RabbitMQ 中的实际应用。 接口回调的概念 接口回调是一种编程模式,用于在异步编程中实现回调机制。它允许…...

大模型日报2024-05-31
大模型日报 2024-05-31 大模型资讯 Anthropic揭示Claude大语言模型的内部机制 摘要: 研究人员将大语言模型的活动模式与特定概念关联起来,并展示了他们可以通过调整这些模式来控制AI模型的行为。 Mistral AI开源新款代码语言模型Codestral 摘要: 人工智能初创公司Mi…...

HarmonyOS 鸿蒙DevEco:导入无法运行提示Sync failed
场景:导入官网下载的案例后导入发现无法运行模拟机,Notifications提示Sync failed... 解决:查看Cause发现是版本问题,通过修改相关内容来解决该问题 1、打开案例地址找到hvigor文件夹 2、打开hvigor-config.json5,将&…...

kafka的安装
windows下kafka的安装 【Kafka】Windows下安装Kafka(图文记录详细步骤)_windows安装kafka-CSDN博客 kafka生产消息 kafka消费消息...

代码随想录算法训练营第36期DAY45
DAY45 1两数之和 [https://www.bilibili.com/video/BV1pt421u7qG/?spm_id_from333.880.my_history.page.click&vd_sourcebaa5f3043be10f96febc0c68c5983df5] 出自B站热血编程系列,主要是复习双指针sum写法、重载比较运算符 class Solution {public: vec…...

springboot+vue 社区养老服务系统
Springbootvue社区居家养老服务系统,数据库mysql,mybatis框架,有可视化页面。 功能: 用户管理 养老服务管理 护理人员管理 服务类型管理 健康状况管理 社区管理 服务区管理 娱乐资讯管理 咨询分类管理 反馈建议 系统简历管理 轮播…...

AI 赋能前端 -- 文本内容概要生成
幸福不在于你获得了什么,而在于你比他人多获得了什么 是比较出来的 大家好,我是柒八九。一个专注于前端开发技术/Rust及AI应用知识分享的Coder 此篇文章所涉及到的技术有 OpenAILangChainRust/WebAssemblyWeb Workerreact+ts+vite配置环境变量(env)因为,行文字数所限,有些概…...
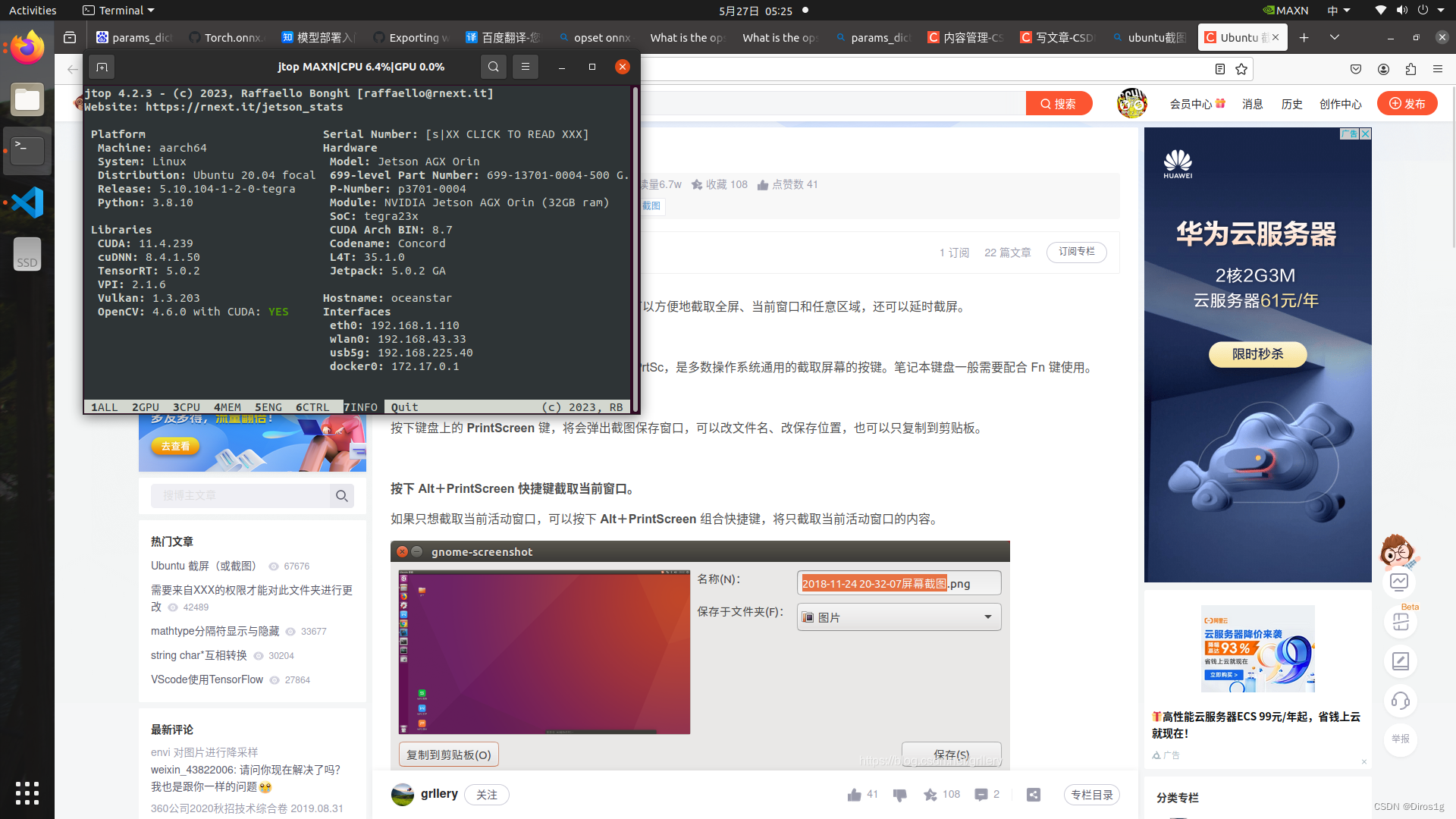
orin部署tensorrt、cuda、cudnn、pytorch、onnx
绝大部分参考https://blog.csdn.net/qq_41336087/article/details/129661850 非orin可以参考https://blog.csdn.net/JineD/article/details/131201121 报错显卡驱动安装535没法安装、原始是和l4t-cuda的部分文件冲突 Options marked [*] produce a lot of output - pipe it t…...

使用javacv对摄像头视频转码并实现播放
要实现Java接受RTSP流解码,并推送给前端实现播放实时流,可以使用一些流媒体处理库,比如JavaCV或者FFmpeg等。以下是一个简单的示例代码: 1.控制层方面的 根据视频rtsp流链接打开转换,通过响应写出流到前台使用flvjs播…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
