模板进阶(仿函数,特化等介绍)
非类型模板参数
模板参数有类型形参和非类型形参;
类型形参:使用typename或者class修饰的参数类型名称
非类型形参:一个普通常量作为模板参数形参,不能为浮点数,字符类型以及类对象;
#include<iostream>
using namespace std;template<class T, size_t N = 64>
class test {private:T data = 10;
public:void print(){cout << data << endl << N << endl;}};int main()
{test<int> a;a.print();return 0;
}上面的代码中,T就是典型的类型形参,N为非类型形参,这个N我们在类函数成员中可以直接使用
模板的特化
我们都知道,使用模板能够很方便的做出能够适应各种场景的函数,比如比较大小,加减法等函数:
template<class T>
bool Less(T a, T b)
{return a < b;
}int main()
{cout << Less(1, 2) << endl;Date a(2022, 7, 8);Date b(2022, 7, 7);cout << Less(a, b)<< endl;return 0;
}
比如这样,就能够比较 int,double 之类的类型,但是有时候我们的类型可能无法满足我们的需求
比如:

我们需要比较的是Date类中的日期大小,但是我们传 Date* 类型进行比较时;
却发现比较的结果实际上是按照地址的大小来进行比较的。
对于这种情况,就需要我们的函数模板的特化出场了;
函数模板特化的步骤
1.有一个基础的函数模板
2.有一个template关键字,后面跟着一个空的<>
3.函数名后跟着一个<>,尖括号中指定需要特化的类型
4.函数形参表必须和模板函数的基础参数类型完全相同,否则会报错
比如上面的 Less 模板函数如何特化?
template<class T>
bool Less(T a, T b)
{return a < b;
}template<>
bool Less<Date*>(Date* a, Date* b)
{return *a < *b;
}我们对比基础函数模板,我们发现,特化的函数模板不仅template后面跟着空的 <> ,而且函数名后还有一个 <> ,并且里面有特化的类型,且形参名都是相同的;
这样我们就能够顺利比较 Date* 类型的参数了;

即然有函数的模板特化,那么就有类的模板特化
类的模板特化和函数的模板特化的规则类似。
类的模板特化
类的模板特化分为两种——全特化和偏特化;
我们先了解简单的全特化
全特化
template<class T1,class T2>
class Test {
public:Test(){cout << "Test(T1,T2)" << endl;}private:T1 a;T2 b;
};template<>
class Test<char, char> {
public:Test(){cout << "Test(char,char)" << endl;}
};int main()
{Test<int, int> t1;Test<char, char> t2;return 0;
}
全特化和函数特化一样,需要有基础的类模板,并且还得有其他一些条件才能实现特化;
若是创建的类对象和特化的类型一致,就会使用特化的类;
偏特化
所谓偏特化就是指这个类并非全都是指定一个类型,而是有特化有没特化的。
template<class T1>
class Test<T1, int> {
public:Test(){cout << "Test(T1,int)" << endl;}
};
就比如这个,我们指定特化第二个参数是 int 类型的,因此若是后面使用 int 类型当做第二个模板参数,就会使用这个类型;
int main()
{Test<int, int> t1;Test<char, char> t2;Test<char, int> t3;return 0;
}
而偏特化里面还有一个更特殊的——针对模板参数进一步条件限制设计出来的特化版本
这个和普通的偏特化不同,它的规则不同,我们先来看看实例;
template<class T1,class T2>
class Test<T1&, T2&> {
public:Test(){cout << "Test(T1&,T2&)" << endl;}
};我们发现,它的template后不是跟着空 <>,其内部有正常的模板参数;
但是类名后面跟着不同指定特化的类型。
这就是进一步限制条件的特化版本。
模板特化应用示例
比如我们使用一个仿函数用来比较函数时,我们有时单纯靠模板无法满足需求,就需要特化版本来满足需求;
template<class T>
class Less {bool operator()(const T&x,const T& y)const {return x < y;}比如这个,我们比较普通的类型无所谓,但是若是比较的是 Date* 的类型时,就会比较地址大小导致出错,因此需要特化。
template<>
class Less<Date*>
{bool operator()(const Date* x, const Date* y){return *x < *y;}
};
模板分离编译
当我们写模板类的时候需要注意一个点——模板类不能分离编译。
什么是分离编译?就是指模板函数或者模板类的函数声明和定义分别在不同的文件。
而模板函数和模板类的声明和定义在不同位置会导致出错。
这是因为编译器对于每个源文件都是独立编译的,若是分离编译则会导致源文件之间没有交互,导致对应的模板没有实例化,从而出错。
具体解决办法就是将声明定义放在一起,从而避免出错。
相关文章:

模板进阶(仿函数,特化等介绍)
非类型模板参数 模板参数有类型形参和非类型形参; 类型形参:使用typename或者class修饰的参数类型名称 非类型形参:一个普通常量作为模板参数形参,不能为浮点数,字符类型以及类对象; #include<iostrea…...
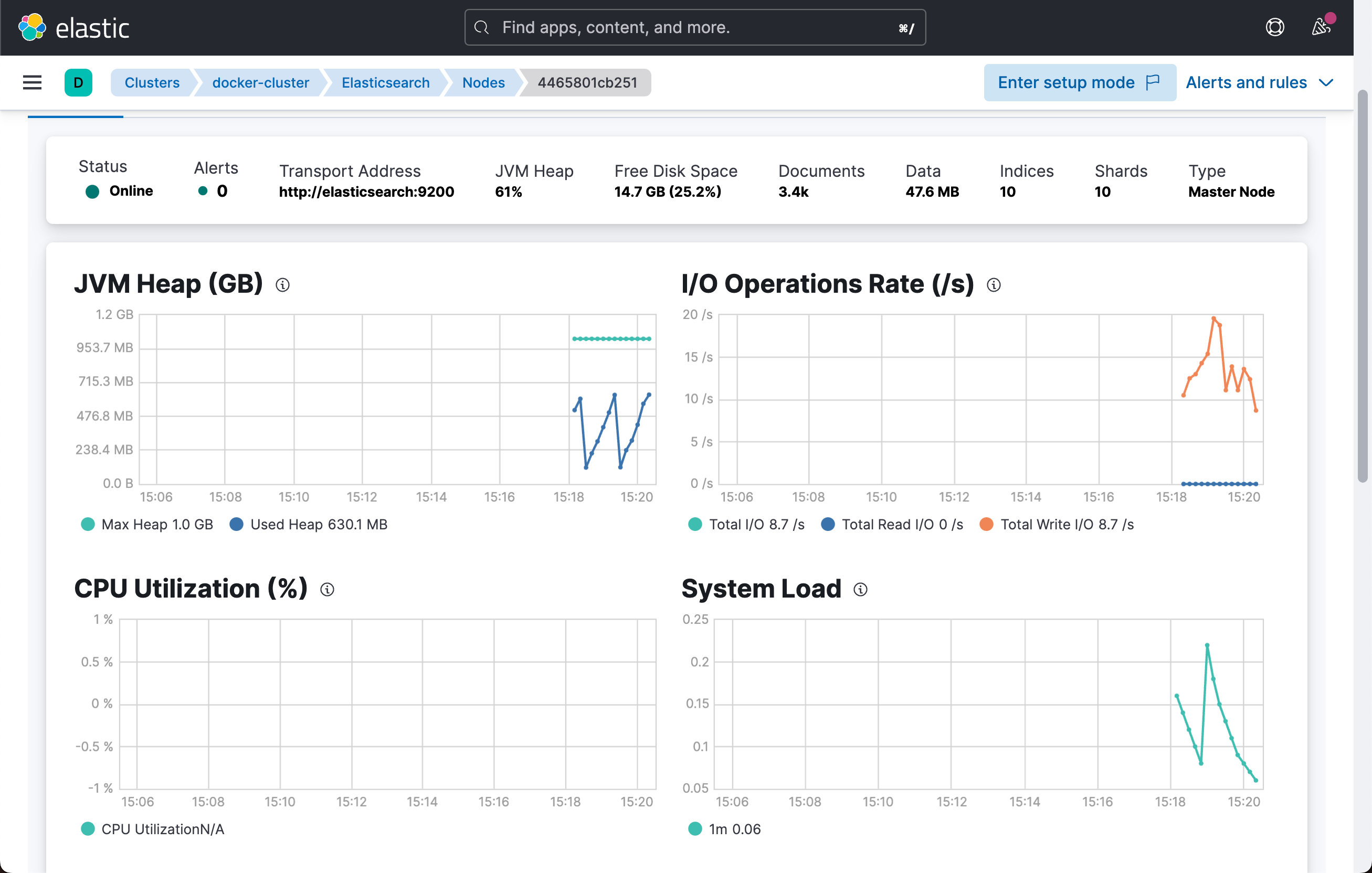
Beats:在 Docker 中同时部署 Metricbeat 和 Elasticsearch
在本教程中,我们将部署一个 metricbeat 来监控正在运行的容器的健康状况和系统指标。 为什么需要监控,为什么需要 Metricbeat? 一个常见的问题,但很少有人回答。 首先,无论我们部署的是 docker 容器还是老式的金属箱&…...

编码技巧——Redis Pipeline
本文介绍Redis pipeline相关的知识点及代码示例,包括Redis客户端-服务端的一次完整的网络请求、pipeline与client执行多命令的区别、pipeline与Redis"事务"、pipeline的使用代码示例; pipeline与client执行多命令的区别 Redis是一种基于客户…...
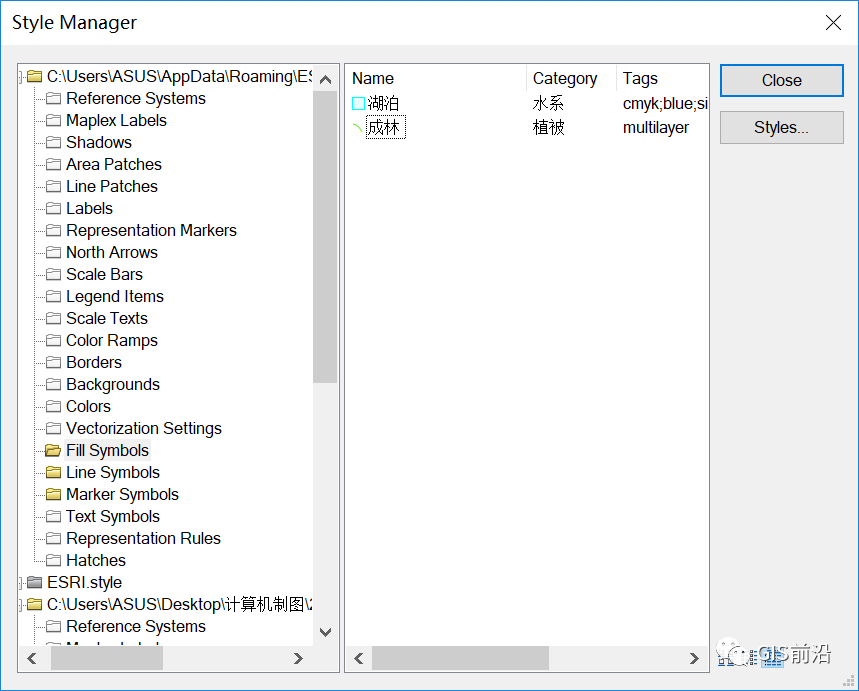
ArcGIS制图技巧:制图入门与点、线、面状符号制作
目的: 1、了解地图制作目的; 2、了解在ArcMap平台中制作地图大致过程。 3、掌握地形图生成的操作; 4、掌握地形图的正确输出方法。 5、理解点状符号、线状符号、面状符号的基本概念; 6、理解地形点状符号、线状符号、面状符…...

Java基础 关于字典数据维护接口设计
开发环境 Eclipse2022JDK1.8 目录 1. 概述 2. 实现步骤 2.1 定义通用接口 2.2 定义实体类 2.3 接口扩展 2.4 接口实现 2.5 功能测试 3. 结语 1. 概述 每一个信息系统或多或少都带有一些数据字典,在维护上,基本上分为增删改查,也就是对数据…...
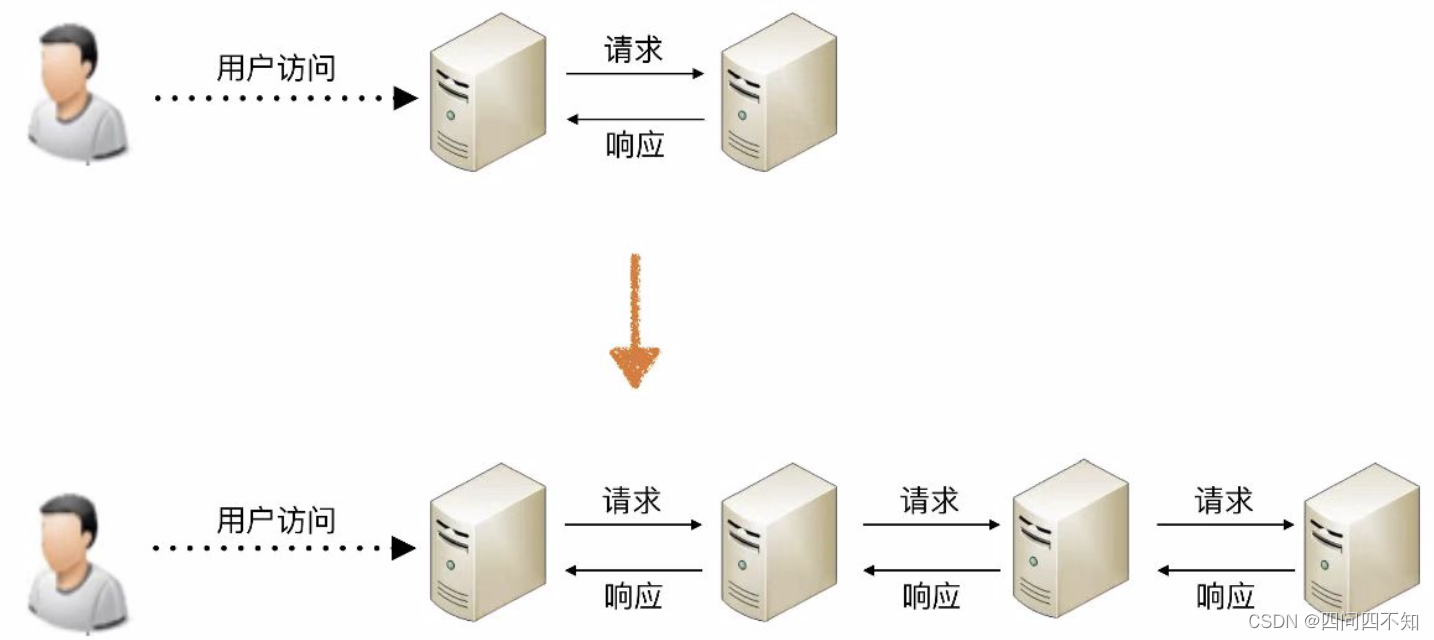
从零开始学架构——复杂度来源
复杂度来源——高性能 对性能孜孜不倦的追求是整个人类技术不断发展的根本驱动力。例如计算机,从电子管计算机到晶体管计算机再到集成电路计算机,运算性能从每秒几次提升到每秒几亿次。但伴随性能越来越高,相应的方法和系统复杂度也是越来越高。现代的计算机CPU集成…...

什么时候需要分表分库?
在当今互联网时代,海量数据基本上是每一个成熟产品的共性,特别是在移动互联网产品中,几乎每天都在产生数据,例如,商城的订单表、支付系统的交易明细以及游戏中的战报等等。对于一个日活用户在百万数量级的商城来说&…...
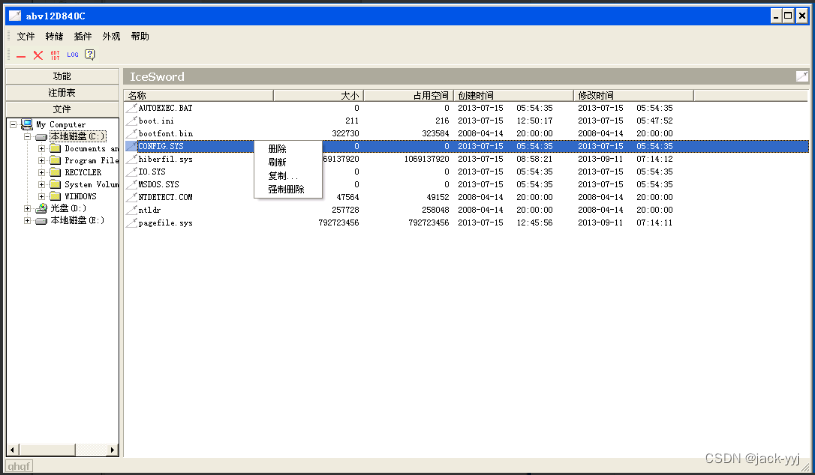
冰刃杀毒工具使用实验(29)
实验目的 (1)学习冰刃的基本功能; (2)掌握冰刃的基本使用方法;预备知识 windows操作系统的基本知识,例如:进程、网络、服务和文件等的了解。 冰刃是一款广受好评的ARK工…...
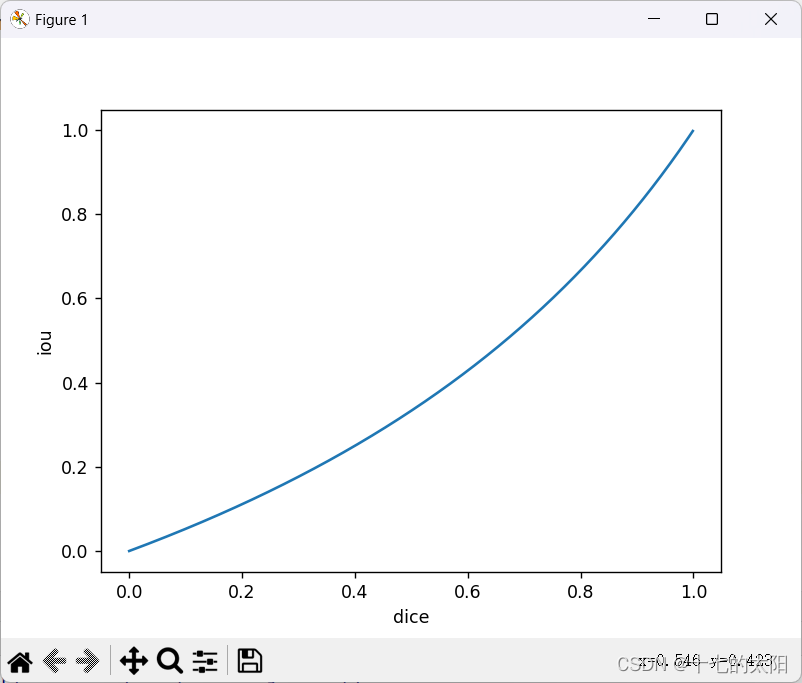
聊聊图像分割的DICE和IOU指标
目录 1. 介绍 2. dice 和 iou 的联系 3. 代码实现 3.1 dice 3.2 iou 3.3 test 3.4 dice 和 iou 的关系曲线 4. 代码 1. 介绍 dice 和 iou 都是衡量两个集合之间相似性的度量 dice计算公式: iou计算公式: iou的集合理解: iou 其实就…...

软件设计师教程(十)计算机系统知识-结构化开发
软件设计师教程 软件设计师教程(一)计算机系统知识-计算机系统基础知识 软件设计师教程(二)计算机系统知识-计算机体系结构 软件设计师教程(三)计算机系统知识-计算机体系结构 软件设计师教程(…...
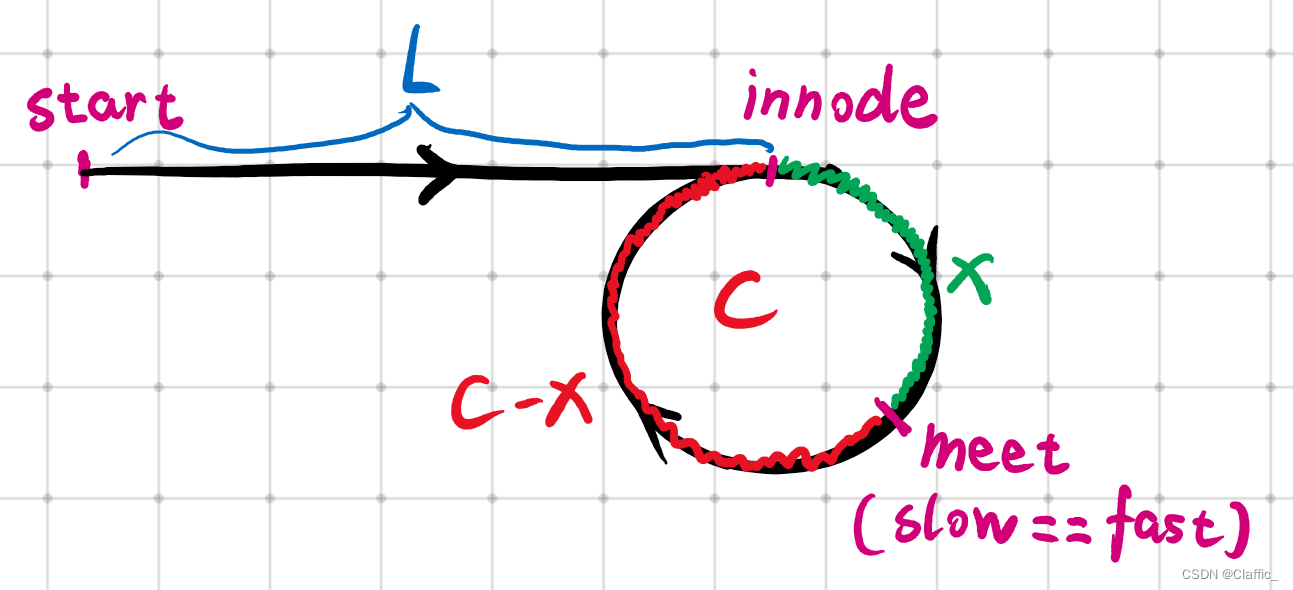
链表OJ之 快慢指针法总结
欢迎来到 Claffic 的博客 💞💞💞 前言: 快慢指针指的是每次指针移动的步长,是解决链表相关的题目的一大利器,下面我将以例题的形式讲解快慢指针法。 目录 一. 链表的中间结点 思路: 代码实…...

C++STL详解(五)——list的介绍与使用
文章目录list的介绍list的使用list的定义方法list迭代器失效问题list插入和删除inserteraselist迭代器的使用begin,end 和 rbegin,rendlist元素访问front 和 backlist容量控制与数据清理resizeclearlist操作函数spliceremove 和 remove_ifuniquemergerev…...
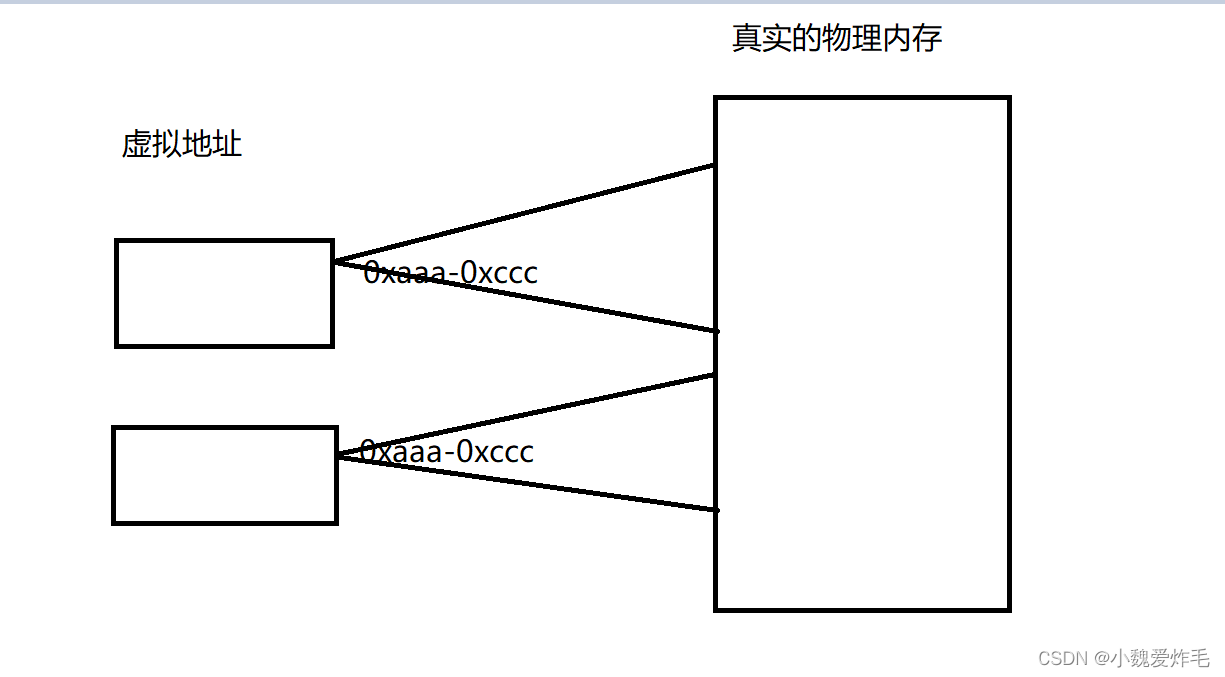
进程和进程的调度
今天,为大家带来进程和进程的调度的学习 1.认识计算机 2.什么是操作系统 3.什么是进程 4.进程管理 5.进程的属性 6.进程的调度 7.进程调度的过程 8.内存分配 1.认识计算机 计算机的组成有五大部分 1.CPU(是计算机的大脑,负责逻辑运算和控制) 2.内存 3.外存 4.输入…...
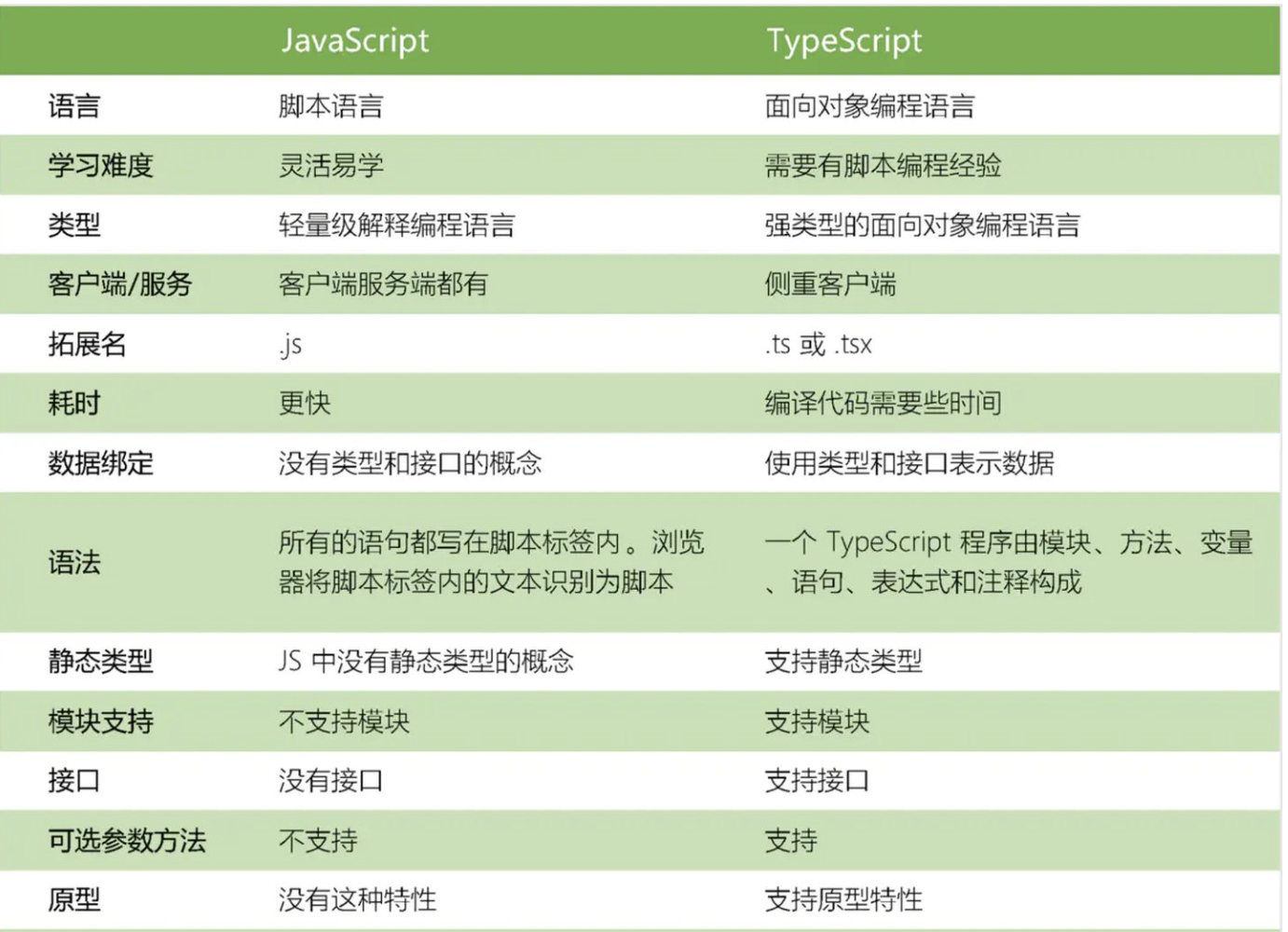
TypeScript 深度剖析:TypeScript 的理解?与 JavaScript 的区别?
一、是什么 TypeScript 是 JavaScript 的类型的超集,支持ES6语法,支持面向对象编程的概念,如类、接口、继承、泛型等 超集,不得不说另外一个概念,子集,怎么理解这两个呢,举个例子,如…...

美颜SDK关键技术讲解——人脸识别与人脸美化
拍摄,自从智能手机普及之后就已经不再是小众爱好,使用手机拍摄记录生活几乎成了人们的日常。在巨量的需求下,美颜工具、美颜SDK已经被广泛应用于各大视频拍摄平台。虽然经常听到美颜SDK,但是大多数人并不了解它,下文小…...
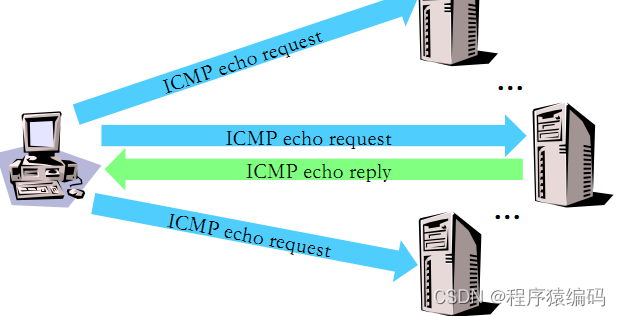
Linux下C/C++ 网络扫描(主机扫描技术)
主机扫描是网络扫描的基础,通过对目标网络中主机IP地址的扫描,从一堆主机中扫描出存活的主机,然后以他们为目标进行后续的攻击。一般会借助于ICMP、TCP、UDP等协议的工作机制,检查打开的进程,开放的端口号等等。 主机…...

无法将“vue-cli-service”项识别为 cmdlet、函数、脚本文件或不是内部命令的原因和解决方案
经常有小伙伴问我说,为什么我们在开发vue项目的时候,需要在package.json的script对象中,去设置命令启动项目,而不是直接的通过"vue-cli-service serve"命令去把项目跑起来。带着这些疑问,小生在此总结了以下…...

逆流程 场景下 处理状态机变化的方案
背景: 针对某些业务场景下,存在逆流程。 比如场景的场景 正向流程如,发起某项申请->对某项申请进行审批。(审批为通过/驳回)。这样这个工作流程就算到最终态。 常见的状态机如, 申请未提交࿰…...

【剧前爆米花--爪哇岛寻宝】Java实现无头单向非循环链表和无头双向链表与相关题目
作者:困了电视剧 专栏:《数据结构--Java》 文章分布:这是关于数据结构链表的文章,包含了自己的无头单向非循环链表和无头双向链表实现简单实现,和相关题目,想对你有所帮助。 目录 无头单向非循环链表实现 …...
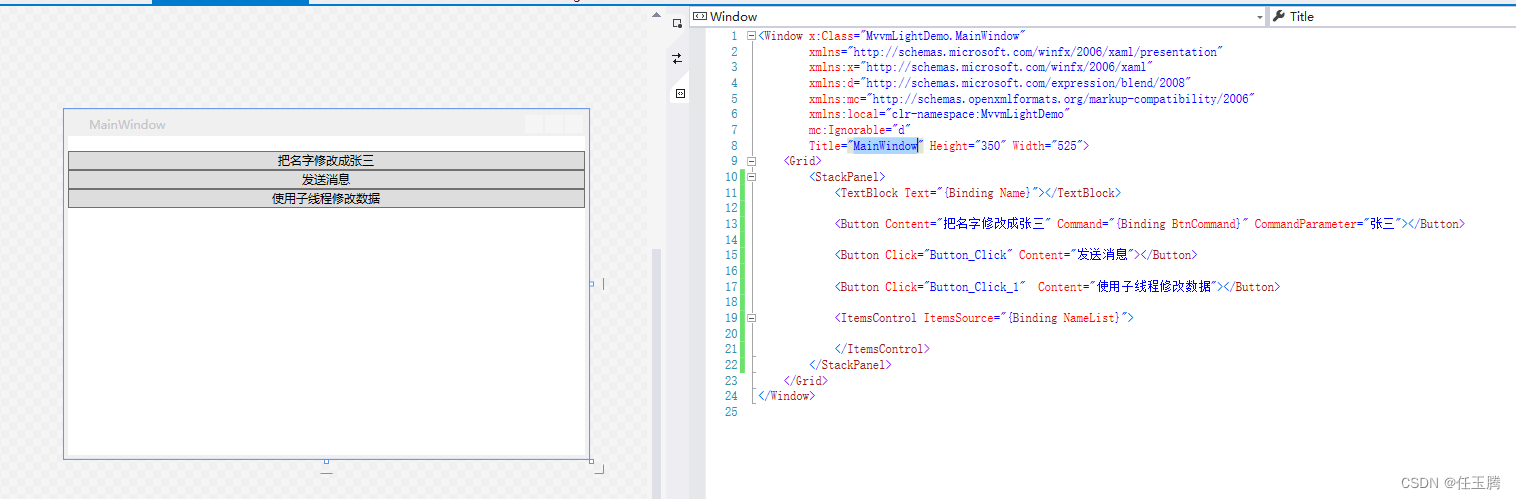
学习MvvmLight工具
最近学习了一下MvvmLight,觉得有些功能还是挺有特色的,所以记录一下 首先新建也给WPF程序 然后在Nuget里面安装MvvmLightLib 包,安装上面那个也可以,但是安装上面那个会自动在代码里面添加一些MvvmLight的demo ,安装M…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
