L3-021 神坛
在古老的迈瑞城,巍然屹立着 n 块神石。长老们商议,选取 3 块神石围成一个神坛。因为神坛的能量强度与它的面积成反比,因此神坛的面积越小越好。特殊地,如果有两块神石坐标相同,或者三块神石共线,神坛的面积为 0.000。
长老们发现这个问题没有那么简单,于是委托你编程解决这个难题。
输入格式:
输入在第一行给出一个正整数 n(3 ≤ n ≤ 5000)。随后 n 行,每行有两个整数,分别表示神石的横坐标、纵坐标(−109≤ 横坐标、纵坐标 <109)。
输出格式:
在一行中输出神坛的最小面积,四舍五入保留 3 位小数。
输入样例:
8
3 4
2 4
1 1
4 1
0 3
3 0
1 3
4 2
输出样例:
0.500
样例解释
输出的数值等于图中红色或紫色框线的三角形的面积。

当你不会时:请记住最简单粗暴的方法(暴力版)

分析原因:是哪超时了呢,是因为什么超时的
得到结论:第三层for循环时,大部分时间都在进行无效的重复计算
大胆尝试:有没有什么办法可以让它不重复或者少重复呢

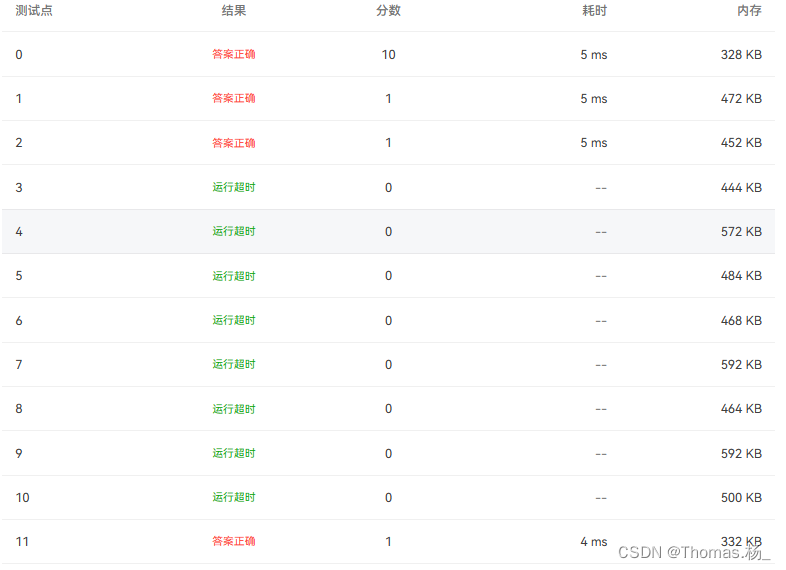
很不幸,还是如此,并没有得到跟多的分数,怎么办
--》时间不够,那就只能放弃了
--》还有时间,我能行,我可以的,我一定行
总结:三层循环嵌套肯定是不行了,我已经进全力优化了,到达极限了,不行啊。
极限分析:既然三层不行,那两层能不能实现呢,多写几个第二层的循环代替第三层行不行呢,试试???!!!

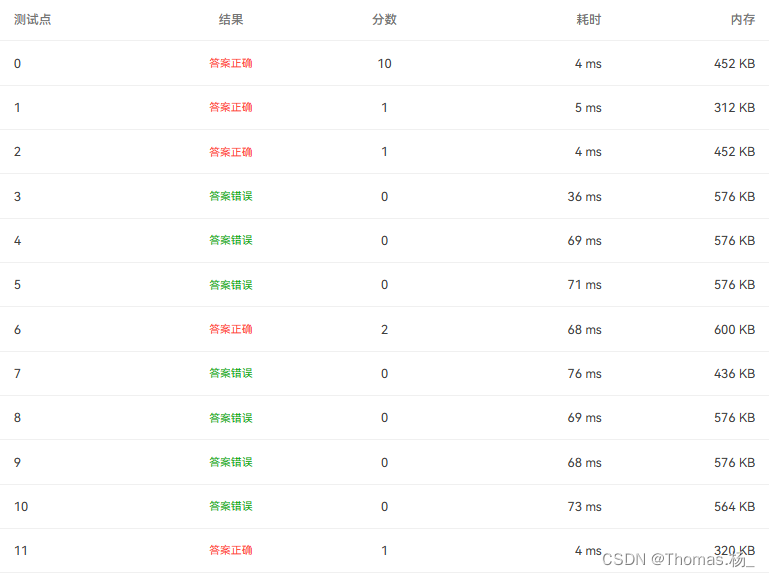
分析:很不错,又混了两分,目的达到了,超时问题已解决,接下来再试试能不能解决答案错误问题。为什么错了呢??????????????
结论:原来是因为 不相邻的两条边组成的三角形也可能比相邻的要小。
再想想办法,马上就要出来了。

//高数下第八章知识 向量的外积 = |a||b|sin <a,b>
// 而三角形的面积公式 S =1/2 |a||b|sin <a,b>

没注意横纵坐标范围(+10^9),MinArea给小了,而且由于有乘法,bouble把不够用
上天总是会眷顾努力的人,不是吗
相信自己,你可以的,你能行
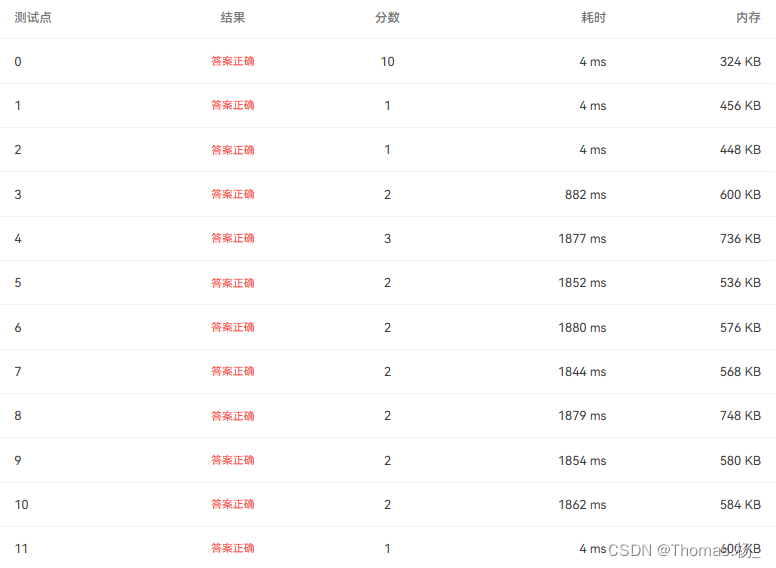
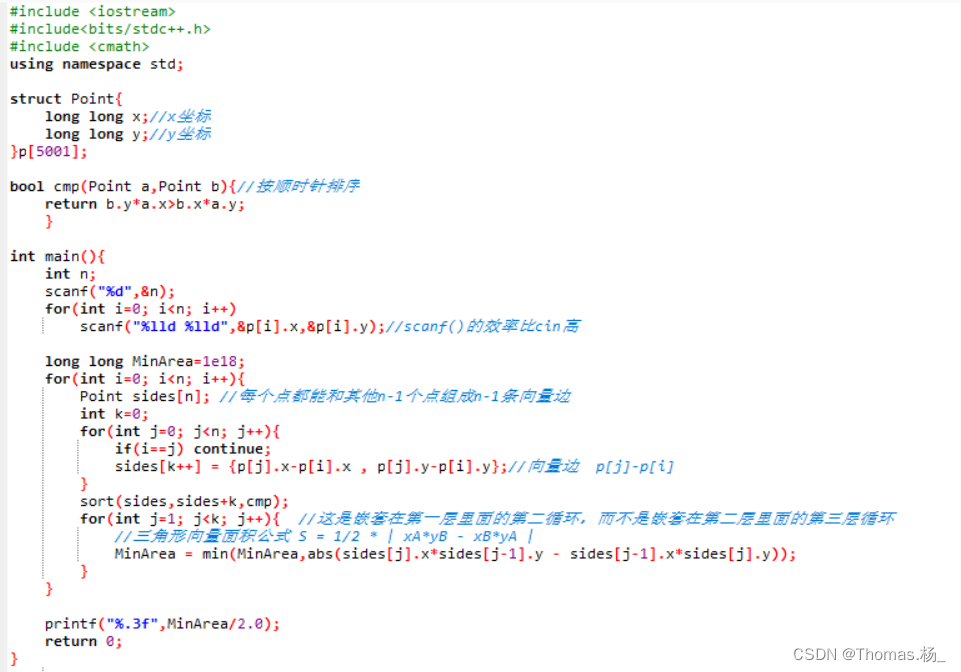
完整源代码:
#include <iostream>
#include<bits/stdc++.h>
#include <cmath>
using namespace std;struct Point{long long x;//x坐标long long y;//y坐标
}p[5001];bool cmp(Point a,Point b){//按顺时针排序return b.y*a.x>b.x*a.y;}int main(){int n;scanf("%d",&n);for(int i=0; i<n; i++)scanf("%lld %lld",&p[i].x,&p[i].y);//scanf()的效率比cin高 long long MinArea=1e18;for(int i=0; i<n; i++){Point sides[n]; //每个点都能和其他n-1个点组成n-1条向量边 int k=0;for(int j=0; j<n; j++){if(i==j) continue; sides[k++] = {p[j].x-p[i].x , p[j].y-p[i].y};//向量边 p[j]-p[i] }sort(sides,sides+k,cmp);for(int j=1; j<k; j++){ //这是嵌套在第一层里面的第二循环,而不是嵌套在第二层里面的第三层循环 //三角形向量面积公式 S = 1/2 * | xA*yB - xB*yA |MinArea = min(MinArea,abs(sides[j].x*sides[j-1].y - sides[j-1].x*sides[j].y)); } } printf("%.3f",MinArea/2.0); return 0;
} 相关文章:

L3-021 神坛
在古老的迈瑞城,巍然屹立着 n 块神石。长老们商议,选取 3 块神石围成一个神坛。因为神坛的能量强度与它的面积成反比,因此神坛的面积越小越好。特殊地,如果有两块神石坐标相同,或者三块神石共线,神坛的面积…...

ArrayList和LinkedList区别
List<TreeNode> list new ArrayList<TreeNode>(); List<TreeNode> allTrees new LinkedList<TreeNode>(); 这两行代码都是用来创建一个存储多个 TreeNode 对象的列表,但是它们使用的底层实现不同。 ArrayList 是一种数组实现的动态数组&…...

977. 有序数组的平方 1. 两数之和 349. 两个数组的交集
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 示例 1: 输入:nums [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:平方后,数组变为 …...
Mysql问题:[Err] 1055 - Expression #1 of ORDER BY clause is not in GROUP BY clause
1 问题描述 使用Navicat连接到MySQL(版本:8.0.18),执行查询: select * from t_user WHERE user_name admin查询结果没有问题,但是报错: [Err] 1055 - Expression #1 of ORDER BY clause is not in GROUP BY claus…...

Idea springboot springCloud热加载热调试常用的两种方式
场景描述 在项目开发的过程中,需要修改调试的时候偶每次都需要重启项目浪费时间,下面是我整理的两种常用的两种方式方式一 修改启动配置方式(主要针对debug模式下) 点击启动配置》edit configrations… configration下面修改Upd…...
银河麒麟V10SP1高级服务器版本离线RPM方式升级openssl openssh 自动化升级系统补丁实战实例全网唯一
银河麒麟高级服务器操作系统简介: 银河麒麟高级服务器操作系统V10是针对企业级关键业务,适应虚拟化、云计算、大数据、工业互联网时代对主机系统可靠性、安全性、性能、扩展性和实时性等需求,依据CMMI5级标准研制的提供内生本质安全、云原生支…...

2023-3-9-一篇简短的文章把C++左右值关系讲的透透彻彻
目录前言C左值和右值二、右值引用二、右值引用前言 对于C的左值和右值相信很多人都没有一个很透彻的了解,之前我也是不懂的时候查阅了好多文章,但是讲完我还是一头雾水,直到我遇到一篇宝藏文章,讲的左值右值的关系以及Move函数的用法是相当的清楚,文章链接在这,话不多说讲解一…...
Vue3这样子写页面更快更高效
在开发管理后台过程中,一定会遇到不少了增删改查页面,而这些页面的逻辑大多都是相同的,如获取列表数据,分页,筛选功能这些基本功能。而不同的是呈现出来的数据项。还有一些操作按钮。 对于刚开始只有 1,2 个页面的时候大多数开发者可能会直接将之前的页面代码再拷贝多…...
)
锐捷AP设置限速(胖模式)
基于整个AP限速命令 Ruijie(config)#wlan-qos ap-based { per-user-limit | total-user-limit } { down-streams | up-streams } average-data-rate average-data-rate burst-data-rate burst-data-rate per-user-limit 对AP上的每个用户进行限速 …...

聚势合力,电巢与SDIA协会“战略合作签约仪式”圆满落成
前言: 2023年03月02日下午,电巢科技与深圳市平板显示行业协会齐聚深圳南山电巢XR演播厅,共同举办了隆重的战略合作签约仪式。 双方就数字化建设、品牌赋能、人才培养、技术创新等企业服务深入合作上达成一致,合力为产业赋能&…...
Linux安装后基础配置--网络--ssh--基本软件
安装教程比较多就不写了。 网络配置 设置虚拟网络 修改网络配置文件 vi /etc/sysconfig/network-scripts/ifcfg-ens33将ONBOOT由no改为yes: 修改为静态网络 /etc/sysconfig/network-scripts/ifcfg-eth33 BOOTPROTOstatic IPADDR192.168.1.129 GATEWAY192.168…...
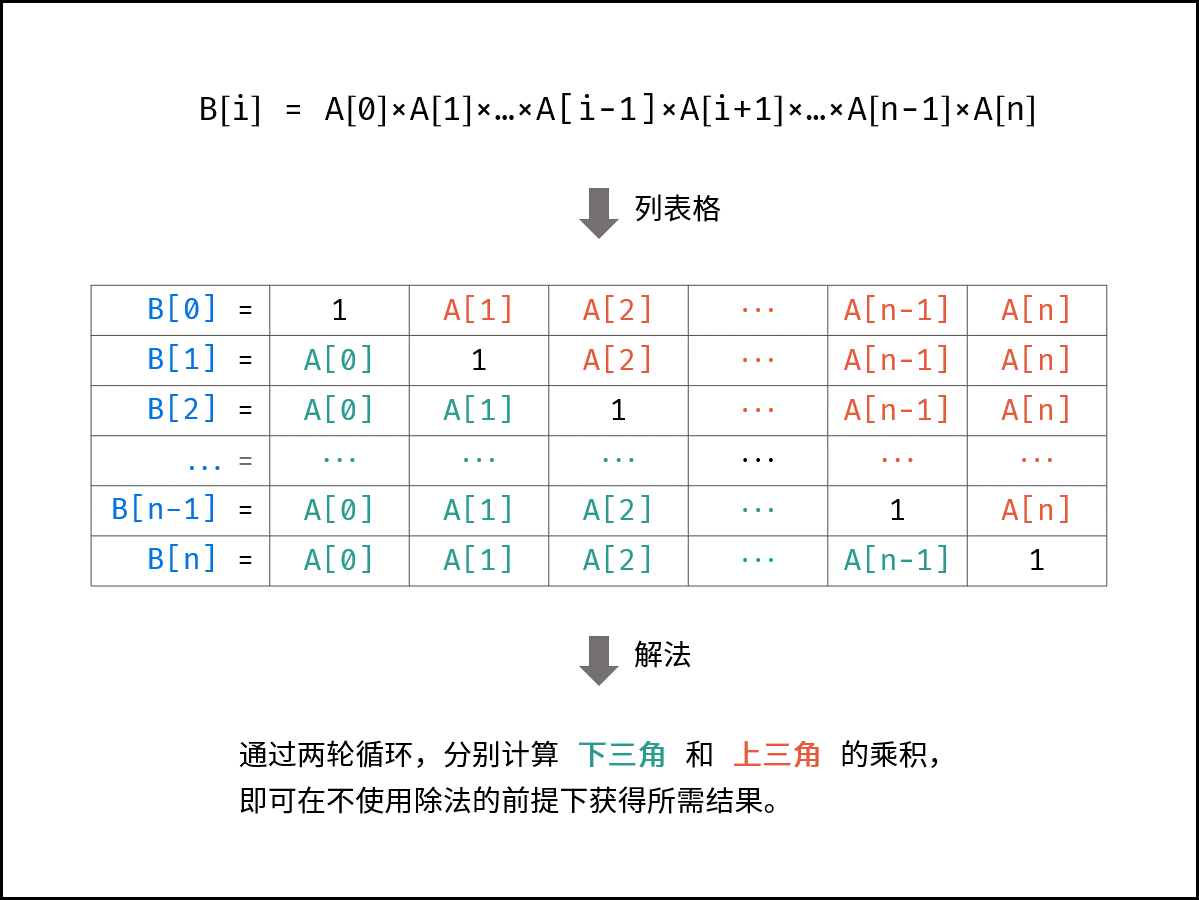
剑指 Offer 66. 构建乘积数组
剑指 Offer 66. 构建乘积数组 难度:middle\color{orange}{middle}middle 题目描述 给定一个数组 A[0,1,…,n−1]A[0,1,…,n-1]A[0,1,…,n−1],请构建一个数组 B[0,1,…,n−1]B[0,1,…,n-1]B[0,1,…,n−1],其中 B[i]B[i]B[i] 的值是数组 AAA…...

1.1 误差的来源
不难发现,考察用计算机解决科学计算问题时所经历的几个环节(如图1-1所示),其中每一步都可能产生误差,首先,数学模型是通过对实际问题进行抽象与简化得到的,它与实际问题之间有误差.数学模型与实…...

python进程间通信
进程间通信表示进程之间的数据交换。 为了开发并行应用程序,需要在进程间交换数据。 下图显示了多个子过程之间同步的各种通信机制 - 各种通信机制 队列 队列可以用于多进程程序。 多处理模块的Queue类与Queue.Queue类相似。 因此,可以使用相同的API…...

麒麟Linux操作系统磁盘策略永久调整为deadline
1.前言在安装数据库,比如达梦数据库时,为获取磁盘最佳性能,一般要将数据磁盘设置为deadline。2. 修改磁盘调度算法2.1临时修改假设磁盘为sda,echo deadline > /sys/block/sda/queue/scheduler2.2通用机永久修改grubby --update-kernelALL …...
)
yum安装Docker(CentOS7.9)
目录 一、安装环境 编写yum源(根据系统版本) 二、安装docker-ce 默认安装docker-ce是最新版本 ps:安装不成功则需要安装container-selinux,下载网络yum源,再安装docker-ce即可 #查看dcoker-ce所产生的文件路径 三、启动docker 四、配置镜像加速器…...
: double free detected)
c++错误 free(): double free detected
记一次bug调试。。。。 我定义了一个类,测试的时候,调用它的方法出现了free(): double free detected ,但是调用其他方法是正常的。这个错误,字面意思就是检测到了双重释放。是指对于同一块内存,释放了两次。 我的类…...

12升400V 升压DC-DC高压脱毛仪解决方案SC3671
ipl(intense pulsed light,强脉冲光)脱毛,也叫光子脱毛,是市场上的一种新型脱毛技术和美容方法,其利用强脉冲光特殊的波长和光热效应实现破坏毛囊并达到永久脱毛的效果,具有速度快,效果好,安全性…...

h264格式分析
h264格式分析一.简介二.h264编码原理1.帧间压缩2.帧内压缩三.编码结构1.IDR帧2.解码顺序四.NALU1.nalu头信息2.annexb模式一.简介 h264是一种视频编码标准,又叫Advanced Video Codec,即AVC 二.h264编码原理 1.帧间压缩 通过I、B、P帧实现帧间压缩 I…...
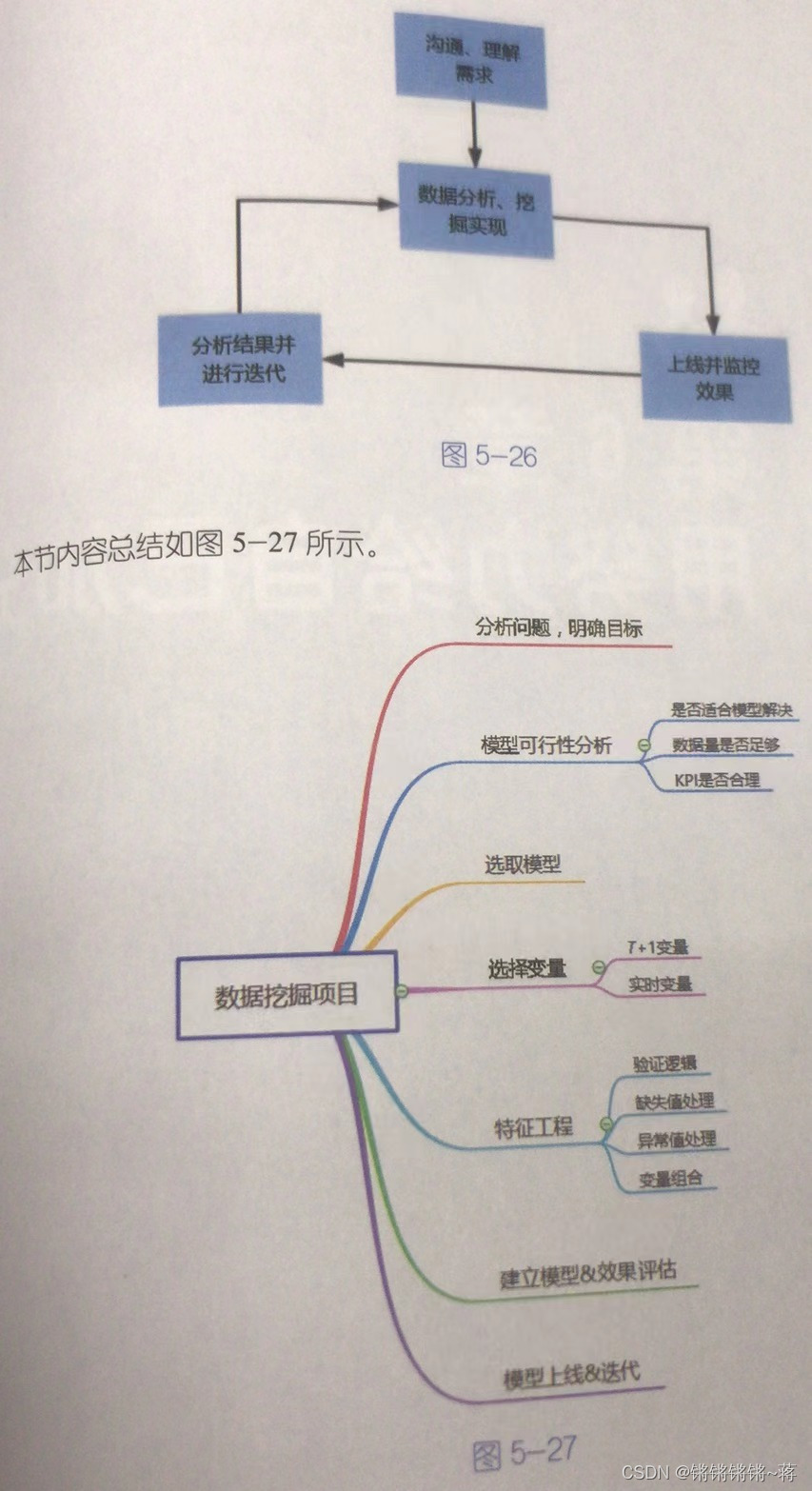
【数据分析师求职面试指南】实战技能部分
文章目录必备技能数据人员如何创造价值完整的指标体系构建数据监控集报表设计设计一份优质的数据分析报告基于互联网大数据的应用A B 测试用户画像完整的数据挖掘项目流程1. 分析问题,明确目标2.模型可行性分析3.选取模型4.选择变量5.特征工程6.建立模型&效果…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
