数据结构练习题——Java实现
20240531-时间复杂度
1、消失的数字

方法一:位运算
两个数字一样的数组,其中一个数组中少了一个数字,定义一个变量分别异或两个数组,结果即为缺少的数字
class Solution {public int missingNumber(int[] nums) {int xor = 0;int n = nums.length;//获取数组长度for (int i = 0; i < n; i++) {//因为该数组少一个数,所以i < nxor ^= nums[i];}for (int i = 0; i <= n; i++) {//假设该数组数字为0~n,不少数字,所以i <= nxor ^= i;}//分别遍历两数组进行异或操作,相同数字异或得零//其他数字均出现两次,只有一个数字出现一次return xor;}}方法二:数学规律
1到n的等差数列的总和,减去当前数组元素的总和,即为缺少的数字
class Solution {public int missingNumber(int[] nums) {int n = nums.length;//等差数列总和 = (首项 + 尾项)* 项数 / 2int total = (1 + n) * n / 2;//当前数组的总和int sum = 0;for(int i=0;i<n;i++){sum += nums[i];}//缺少值 = 等差数列总和 - 数组总和return total - sum;}
}2、旋转数组

这个不会,暂且搁置
3、给定一个整数sum,从有N个有序元素的数组中寻找元素a,b,使得a+b的结果最接近sum,最快的平均时间复杂度是( )
A.O(n)
B.O(n^2)
C.O(nlogn)
D.O(logn)
选B了
解析:
正确答案A,数组元素有序,所以a,b两个数可以分别从开始和结尾处开始搜索,根据首位元素的和是否大于sum,决定搜索的移动,整个数组被搜索一遍,就可以得到结果,所以时间复杂度为O(n)
4、设某算法的递推公式是T(n)=T(n-1)+n,T(0)=1,则求该算法中第n项的时间复杂度为()
A.O(n)
B.O(n^2)
C.O(nlogn)
D.O(logn)
解析:

5、分析以下函数的时间复杂度
void fun(int n) {int i=l;while(i<=n)i=i*2;
}A.O(n)
B.O(n^2)
C.O(nlogn)
D.O(logn)
解析:
D,此函数有一个循环,但是循环没有被执行n次,i 每次都是2倍进行递增,所以只会被执行![]()
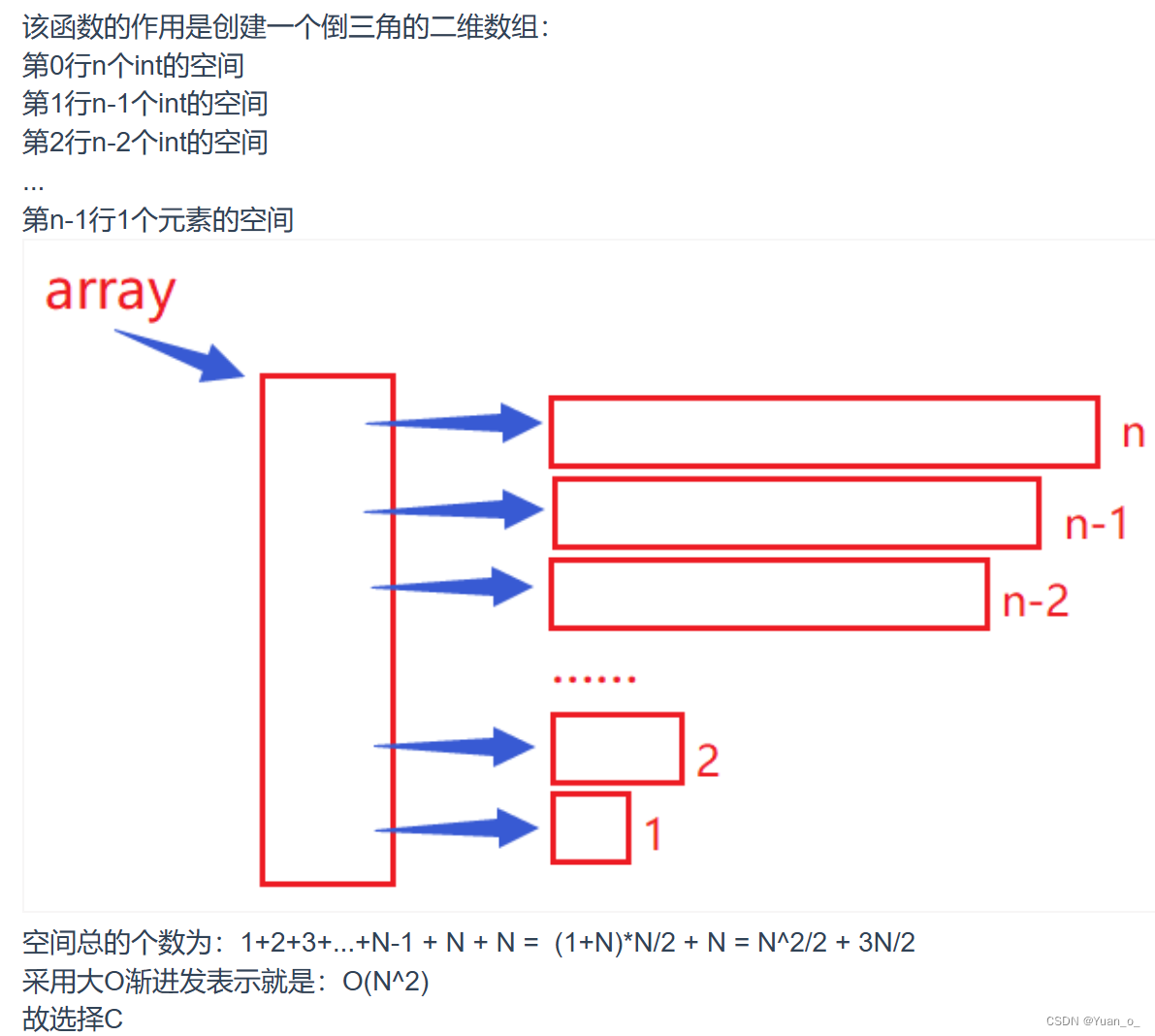
6、分析以下函数的空间复杂度
public static int[][] get2Array(int n){int[][] array = new int[n][];for(int i = 0; i < n; i++) {array[i] = new int[n-i];n--;}return array;
}A.O(1)
B.O(N)
C.O(N^2)
D.O(logN)
解析:
相关文章:

数据结构练习题——Java实现
20240531-时间复杂度 1、消失的数字 方法一:位运算 两个数字一样的数组,其中一个数组中少了一个数字,定义一个变量分别异或两个数组,结果即为缺少的数字 class Solution {public int missingNumber(int[] nums) {int xor 0;int…...
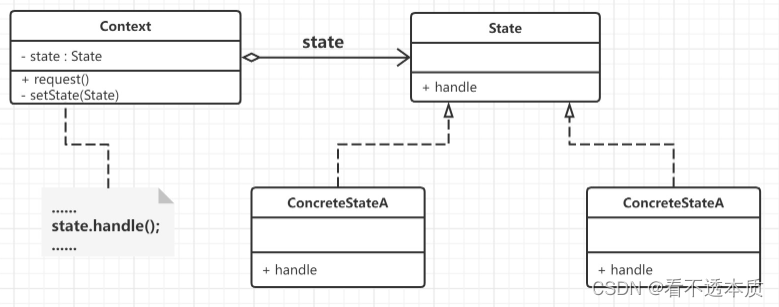
行为设计模式之状态模式
文章目录 概述定义结构图 2.代码示例小结 概述 定义 状态模式(state pattern)的定义: 允许一个对象在其内部状态改变时改变它的行为。 对象看起来似乎修改了它的类。 状态模式就是用于解决系统中复杂对象的状态转换以及不同状态下行为的封装问题.。状态模式将一个对象的状态…...
找回以前的视频:技术与实践3个指南
你们有没有发现现在视频已经成为我们生活中不可或缺的一部分了?不管是在工作场合做演示、在学习时看教学视频,还是在休闲娱乐时追剧看电影,视频都扮演着超级重要的角色。 然而误删或手机故障的发生很可能将以前的视频清除。本文将深入探讨手…...

GCN 代码解析(一) for pytorch
Graph Convolutional Networks 代码详解 前言一、数据集介绍二、文件整体架构三、GCN代码详解3.1 utils 模块3.2 layers 模块3.3 models 模块3.4 模型的训练代码 总结 前言 在前文中,已经对图卷积神经网络(Graph Convolutional Neural Networks, GCN&am…...

2024年云计算、信号处理与网络技术国际学术会议(ICCCSPNT 2024)
2024年云计算、信号处理与网络技术国际学术会议(ICCCSPNT 2024) 2024 International Academic Conference on Cloud Computing, Signal Processing, and Network Technology(ICCCSPNT 2024) 会议简介: 2024年云计算、…...
希尔排序法
希尔排序为插入排序的优化,即将数组分组,将每一组进行插入排序,每一组排成有序后,最后整体就变有序了。 上面gap2,即5,14,18,27,68为一组;13,20&a…...

thinkphp6.0版本下子查询sql处理
目录 一:背景 二:查询实例 三:总结 一:背景 我们在实际业务的开发过程中,经常会碰到这样的场景,查询某些部门的客户信息,查询下过订单的客户信息。这里查询客户信息实际上就用到了子查询&…...
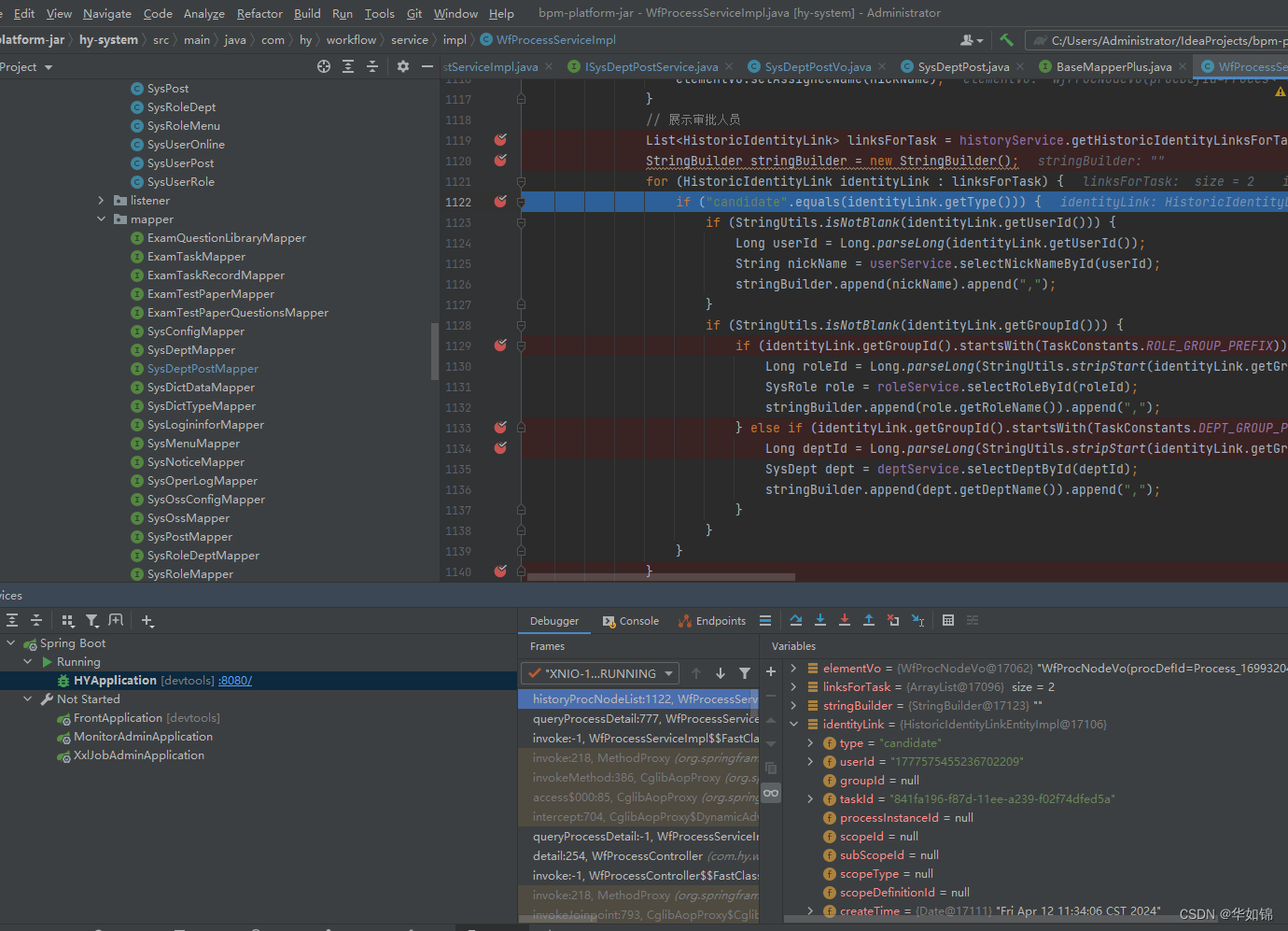
flowable工作流 完成任务代码 及扩展节点审核人(实现多级部门主管 审核等)详解【JAVA+springboot】
低代码项目 使用flowable 工作流 完成任务代码 详解 可以看到 complete()方法 传递了流程变量参数var 前端传递此参数就可以实现 流程中 审批 更新流程变量参数var 也可以进行更多扩展 实现流程中更新表单内容功能 启动流程实例代码 实现对于流程自定义 动态节点审核人 功…...

【电源专题】一体成型电感为什么需要注意耐压问题
对于电感,我们在电路上使用的很多,如升压、降压、滤波等电路中基本上使用到了电感。电感的种类有很多,电感从不同的角度会有不同的分类。如可以根据否屏蔽、工艺类型、磁性材料类型等可分为多类,这在文章:【分立元件】电感器(inductor)——简介中有做了一些简单的介绍。…...

如何看待时间序列与机器学习?
GPT-4o 时间序列与机器学习的关联在于,时间序列数据是一种重要的结构化数据形式,而机器学习则是一种强大的工具,用于从数据中提取有用的模式和信息。在很多实际应用中,时间序列与机器学习可以结合起来,发挥重要作用。…...

vue图标不显示
静态:有可能路径错误 <img src"../../assets/images/index1.png"> <img src"/assets/images/index2.png"> 动态:需要解析 <div v-for"item in userList" :key"item.id"> <img :src"getUrl(i…...

文件夹如何加密码全攻略,5个文件夹加密方法新手也能学
文件夹如何加密码?在这个互联网时代,隐私保护越来越受到大家的重视。我们在日常工作中,有时候会接触一些比较重要的文件,为了不让这些文件信息被泄露,所以我们可以给文件夹设置密码保护。那要怎么给文件夹设置密码呢&a…...

useState和store的区别
useState 和 useStore 是 React 应用中用于管理数据状态的两种不同的 Hook。它们在功能和用途上有一些区别: useState useState 是 React 提供的一个 Hook,用于在函数组件中添加局部状态。每个 useState 调用都会返回一个数组,包含两个元素…...
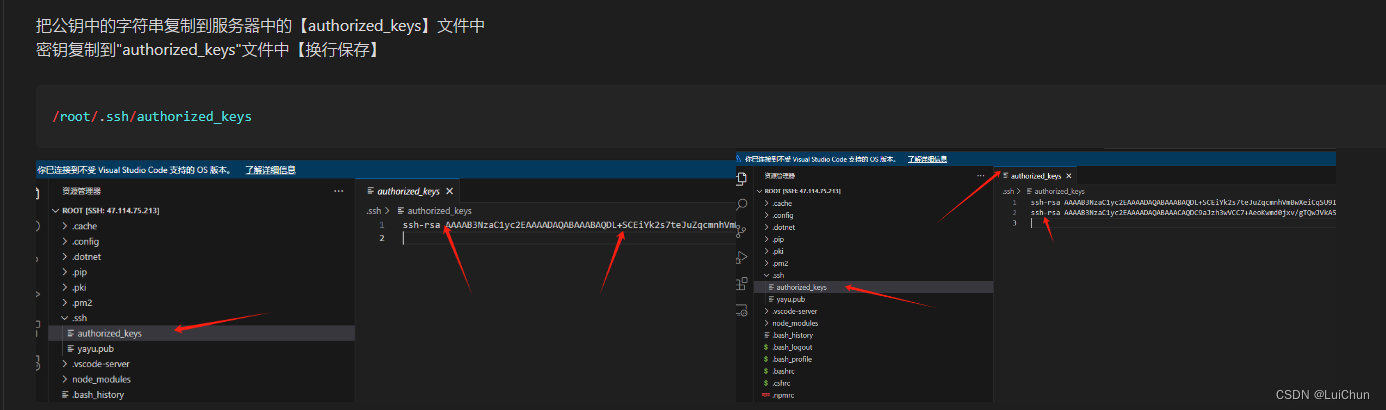
vscode远程登录阿里云服务器【使用密钥方式--后期无需再进行密码登录】【外包需要密码】
1:windows主机上生成【私钥】【公钥】 1.1生成公钥时不设置额外密码 1.2生成公钥时设置额外密码【给外包人员使用的方法】 2:在linux服务器中添加【公钥】 3:本地vscode连接linux服务器的配置 操作流程如下 1.1本地终端中【生成免密登录…...

解决uniapp里的onNavigationBarSearchInputClicked不生效
如何在uniapp里使用onNavigationBarSearchInputClicked。 1、在page.json里配置 "pages": [{"path": "pages/index/index","style": {"navigationBarTitleText": "首页","navigationStyle": "cu…...

Windows下搭建Cmake编译环境进行C/C++文件的编译
文章目录 1.下载Cmake2.安装MinGW-w643.进行C/C文件的编译 1.下载Cmake 网址:https://cmake.org/download/ 下载完成后安装,勾选“Add CMake to the system PATH for the current user" 点击Finish完成安装,在cmd窗口验证一下是否安…...

实用新型专利申请材料的撰写与准备
在科技创新日益活跃的今天,实用新型专利的申请与保护显得尤为重要。实用新型专利作为一种重要的知识产权形式,对于推动科技进步、促进经济发展具有重要意义。 首先我们需要明确实用新型专利的定义。实用新型专利是指对产品的形状、构造或者其结合所提出…...

代码随想录算法训练营第60天|● 84.柱状图中最大的矩形
84. 柱状图中最大的矩形 和昨天的思路完全一样 单调栈直接解了 双指针法特别麻烦 class Solution:def largestRectangleArea(self, heights: List[int]) -> int:heights.insert(0,0)heights.append(0)stack[0]res0for i in range(1,len(heights)):while stack and heights…...

让AI给你写代码(9.3):一点改进,支持扩展本地知识库
改进目标,当输入提示问题后,能匹配到本地知识库的需求,然后AI按匹配到的需求给出代码并进行自动测试; 如果无法匹配到本地需求,可以直接输入生成逻辑,再由AI生成,然后支持用户把新需求插入本地库…...

探索煤化工厂巡检机器人的功能、应用及前景
大家都知道、煤化工厂是以煤为原料生产化工产品的工厂,存在易燃易爆、高温、中毒等隐患等。因此,对煤化工厂进行巡检是非常必要的。巡检旨在是定时对厂内设备运行异常、泄漏等问题,并及时进行处理,保障工作场所的安全。除了以上存…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
