刷题记录(20240605)
1.数组构造
题目描述
小红的数组构造小红希望你构造一个数组满足以下条件:
1.数组共有 n个元素,且所有元素两两不相等。
2.所有元素的最大公约数等于 k。
3.所有元素之和尽可能小。请你输出数组元素之和的最小值。
输入描述:
两个正整数 n 和 k。
输出描述:
一个正整数,代表数组元素之和的最小值,
输入示例:
3 1
输出示例:6
分析:
数组只能是 1k,2k,3k,……,(n-1)k,nk
求和可以用等差数列求和公式 (n+1)nk/2
代码:
#include <iostream>
using namespace std;int main() {long long result = 0;int n, k;cin >> n >> k;// 使用等差数列求和公式进行计算result = k * (n * (n + 1LL) / 2);cout << result << endl;return 0;
}2.精华帖子
题目描述
小红书的推荐帖子列表为 [0,n),其中所有的帖子初始状态为"普通",现在运营同学把其中的一些帖子区间标记为了“精华"。
运营同学选择了固定长度 k,对整个帖子列表截取,要求计算在固定的截取长度k下,能够截取获得的最多精华帖子数量。
输入描述
第一行输入三个正整数 n,m,k,分别代表初始帖子列表长度,精华区间的数量,以及运营同学准备截取的长度。
接下来的 m 行,每行输入两个正整数,| 和r,代表第i个左闭右开区间。
1 <= k<=n<= 20000000.
1<= m <= 100000.
0 <=l<ri<= n,保证任意两个区间是不重复的。
输出描述
一个正整数,代表截取获得的最多的精华帖子数量。
输入示例
5 2 3
1 2
3 5
输出示例2
思路:
1.按照n,m,k构造输入序列v
2.先遍历前k个,统计精华帖子数量,再便利第k+1个,每次加上第i个,减掉第i-k个的值即可
3.返回最大的数量
代码:
#include<iostream>
#include <vector>
using namespace std;
int main(){int n,m,k;cin>>n>>m>>k;vector<vector<int>> p;while(m--){int a,b;cin>>a>>b;vector<int> p1 = {a,b};p.push_back(p1);}vector<int> v(n,0);for(auto it:p){for(int i = it[0];i<it[1];i++){v[i] = 1;}}int res = 0;int sum = 0;for(int i = 0;i<k;i++){res +=v[i];}sum = res;for(int i = k;i<n;i++){sum = sum + v[i] - v[i-k];res = max(res,sum);}cout<<res<<endl;}3.连续子数组最大和
题目描述
小红拿到了一个数组,她希望进行最多一次操作:将一个元素修改为x。小红想知道,最终的连续子数组最大和最大是多少?
输入描述
第一行输入一个正整数t,代表询问次数。对于每次询问,输入两行:
第一行输入两个正整数n和x。代表数组的大小,以及小红可以修改成的元素。第二行输入n个正整数a_i,代表小红拿到的数组
输出描述
输出t行,每行输出一个整数,代表连续子数组的最大和。
输入示例
3
5 10
5 -1 -5 -3 2
2 -3
-5 -2
6 10
4 -2 -11 -1 4 -1
输出示例15
-2
15
思路:(代码随想录)
动态规划:最大子序和 的方法,先求出 [0 - i) 区间的 最大子序和 dp1 和 (i, n)的最大子序和dp2
然后在遍历一遍i, 计算 dp1 + dp2 + vec[i] 的最大值就可以。
正序遍历,求出 [0 - i) 区间的 最大子序,dp[ i - 1] 表示 是 以 下标 i - 1为结尾的最大连续子序列和为dp[i - 1]。
所以 在计算区间 (i, n)即 dp2 的时候,我们要倒叙。因为我们求的是以 包括下标i + 1为起始位置的最大连续子序列和为dp[i + 1]。
这样 dp1 + dp2 + vec[i] 才是一个完整区间。
代码:
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main() {int t, n, x;cin >> t;while (t--) {cin >> n >> x;vector<int> vec(n);for (int i = 0; i < n; i++) cin >> vec[i];vector<int> dp1(n);dp1[0] = vec[0];int res = vec[0];// 从前向后统计最大子序和for (int i = 1; i < n; i++) {dp1[i] = max(dp1[i - 1] + vec[i], vec[i]); // 状态转移公式res = max(res, dp1[i]);}res = max(res, vec[n - 1]);// 从后向前统计最大子序和vector<int> dp2(n);dp2[n - 1] = vec[n - 1];for (int i = n - 2; i >= 0; i--) {dp2[i] = max(dp2[i + 1] + vec[i], vec[i]);}for (int i = 0 ; i < n ; i++) {int dp1res = 0;if (i > 0) dp1res = max(dp1[i-1], 0);int dp2res = 0;if (i < n - 1 ) dp2res = max(dp2[i+1], 0);res = max(res, dp1res + dp2res + x);}cout << res << endl;}}
相关文章:
)
刷题记录(20240605)
1.数组构造 题目描述 小红的数组构造小红希望你构造一个数组满足以下条件: 1.数组共有 n个元素,且所有元素两两不相等。 2.所有元素的最大公约数等于 k。 3.所有元素之和尽可能小。请你输出数组元素之和的最小值。 输入描述: 两个正整数 n 和 k。 输出描述ÿ…...

CUDA和OpenGL纹理texture结合
cuda和OpenGL纹理结合,并进行直方图计算 针对于单通道16位图像。结合方式在CUDA_equalizeHistogram_16函数中。 其他的为CUDA核函数。 #define HISTOGRAM_LENGTH 65536 // 2^16 表示16位深度定义直方图长度为65536,对应16位像素值的范围(0-65535)。 __global__ void com…...
市场凌乱,智能算法哪种效果好?
当我们在面对市场波动,个股震荡,无从下手的时候,不懂算法的朋友就只懂做t;懂算法的朋友这会儿就迷茫并不知道选择哪种智能算法交易?今天小编给大家整理一套性价比高的,适合个人投资者搞的算法交易ÿ…...

学会这14大招,30天涨粉两三千没问题!沈阳新媒体运营培训
很多小白在刚转入公司做新媒体时,基本都是从帮助公司运营账号开始的。但不同于个人号,一个企业本身是没有ip属性的,它的风格、调性等,都需要通过你的运营,让它变成一个活灵活现的、赋予独立个性人设的账号。 目前&…...

SQL数据库性能优化
1.查询尽量避免使用select * 1.1 增加磁盘开销:数据库本质上是将记录存储在磁盘上,查询操作就是一种进行磁盘IO的行为,我们查询的字段越多,读取的内容也就越多,对IO磁盘的开销也就会增大,特别是某些字段,如…...

eNSP学习——RIP路由协议基础配置
目录 主要命令 原理概述 实验内容 实验目的 实验拓扑 实验编址 实验步骤 1、基本配置 2、使用RIPv1搭建网络 开启 RIP调试功能 3、使用RIPv2搭建网络 RIPv1和RIPv2的不同 需要eNSP各种配置命令的点击链接自取:华为eNSP各种设备配置命令大全PD…...
)
备考系统架构设计师,看这篇就够了!(包括核心总结、真题、论文、模拟试题索引)
注:以下章节核心总结来自最新版课本:系统架构设计师教程(第2版): https://url35.ctfile.com/f/52515535-1268514286-ca9b3a?p6235 ( 访问密码: 6235, 电子版 pdf 文件大小: 168.9 M ,需要的话可自行下载,…...

stm32编译原理
STM32编译原理主要包括以下几个方面: (1)编译器选择:STM32可以使用多种编译器进行开发,如Keil、IAR、GCC等。不同的编译器有不同的特点和优缺点,需要根据具体需求进行选择。 (2)编…...

如何以JNI方式实现安卓APP控制GPIO?
本文档提供了在 Android 10 设备上通过应用程序(App)控制通用输入输出(GPIO)的详细指南。这涵盖了从创建 gpio驱动到App 配置 以及 SELinux 策略以允许特定访问的所有必要步骤。 1. 驱动实现 添加创建gpio控制驱动bsp\kernel\ke…...

计算机网络学习笔记——运输层(b站)
目录 一、 运输层概述 二、运输层端口号、复用与分用的概念 三、UDP和TCP的对比 四、TCP的流量控制 五、TCP的拥塞控制 六、TCP超时重传时间的选择 七、TCP可靠传输的实现 八、TCP报文段的首部格式 一、 运输层概述 物理层、数据链路层、网络层实现了主机到主机的通信…...
)
HBase数据库面试知识点:第二部分 - 核心技术(持续更新中)
目录 1. 分布式存储与HDFS 2. 面向列的存储 3. 数据版本控制 4. Region与RegionServer 5. 分布式协调服务(ZooKeeper) 1. 分布式存储与HDFS HBase利用Hadoop的HDFS作为其底层存储系统,确保数据的高可靠性和可扩展性。 数据块࿰…...
Spring 使用SSE(Server-Sent Events)学习
什么是SSE SSE 即服务器发送事件(Server-Sent Events),是一种服务器推送技术,允许服务器在客户端建立连接后,主动向客户端推送数据。 SSE 基于 HTTP 协议,使用简单,具有轻量级、实时性和断线重…...
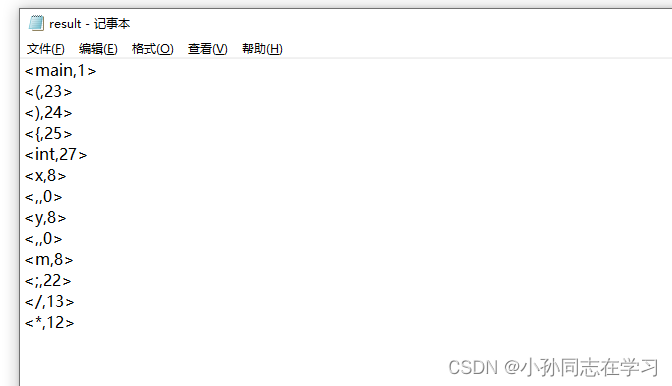
词法分析器的设计与实现--编译原理操作步骤,1、你的算法工作流程图; 2、你的函数流程图;3,具体代码
实验原理: 词法分析是编译程序进行编译时第一个要进行的任务,主要是对源程序进行编译预处理之后,对整个源程序进行分解,分解成一个个单词,这些单词有且只有五类,分别时标识符、关键字(保留字&a…...

linux查看磁盘类型命令
在Linux中,有多种方法可以查看磁盘是固态硬盘(SSD)还是机械硬盘(HDD)。以下是一些常用的方法: 查看/sys/block/目录 /sys/block/目录包含了系统中所有块设备的信息。你可以查看这个目录中的设备属性来判断…...

多线程调用同一个不包含可变状态,并且是线程安全的方法时,可同时执行,不必等待排队
多线程调用同一个不包含可变状态,并且是线程安全的方法时,可同时执行,不必等待排队 前言同时执行方法的条件示例并发执行的优势实验验证总结 前言 如果方法不包含可变状态,并且是线程安全的,那么在高并发环境下&#…...

Java文件操作①——XML文件的读取
系列文章目录 文章目录 系列文章目录前言一、邂逅XML二、应用 DOM 方式解析 XML三、应用 SAX 方式解析 XML四、应用 DOM4J 及 JDOM 方式解析 XMLJDOM 方式解析 XMLDOM4J 方式解析 XML前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。…...
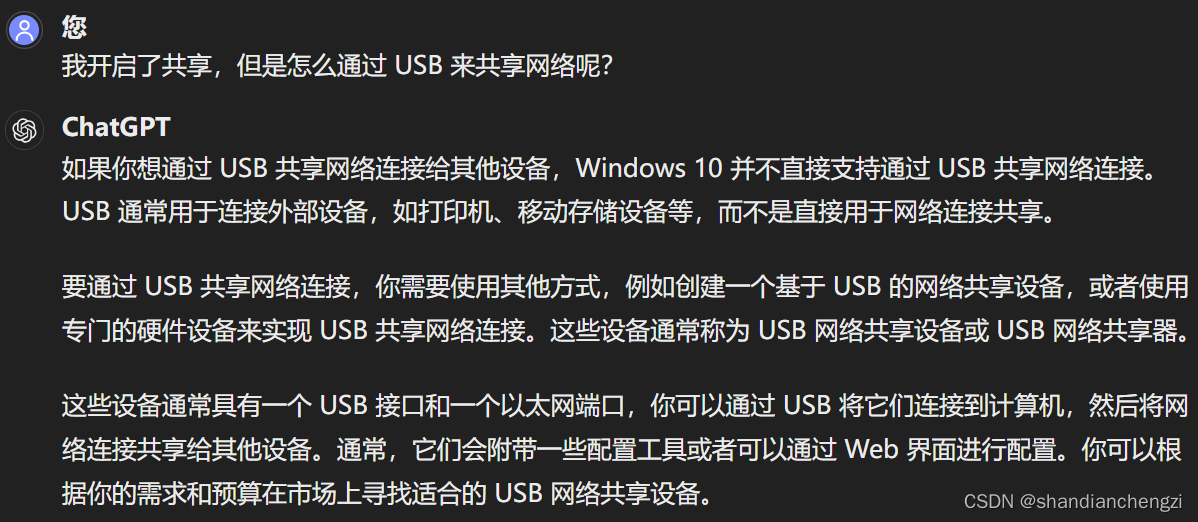
【记录】网络|没有路由器没有网线,分别使用手机或Windows电脑共享网络给ARM64开发板,应急连接
事情是这样的,我的开发板明明已经选择了记住热点 WiFi 密码,但是却没有在开机的时候自动连接,我又没有放显示器在身边,又不想为了这点事去找个显示器来,就非常难受。 我手边有的设备是: 笔记本电脑&#…...
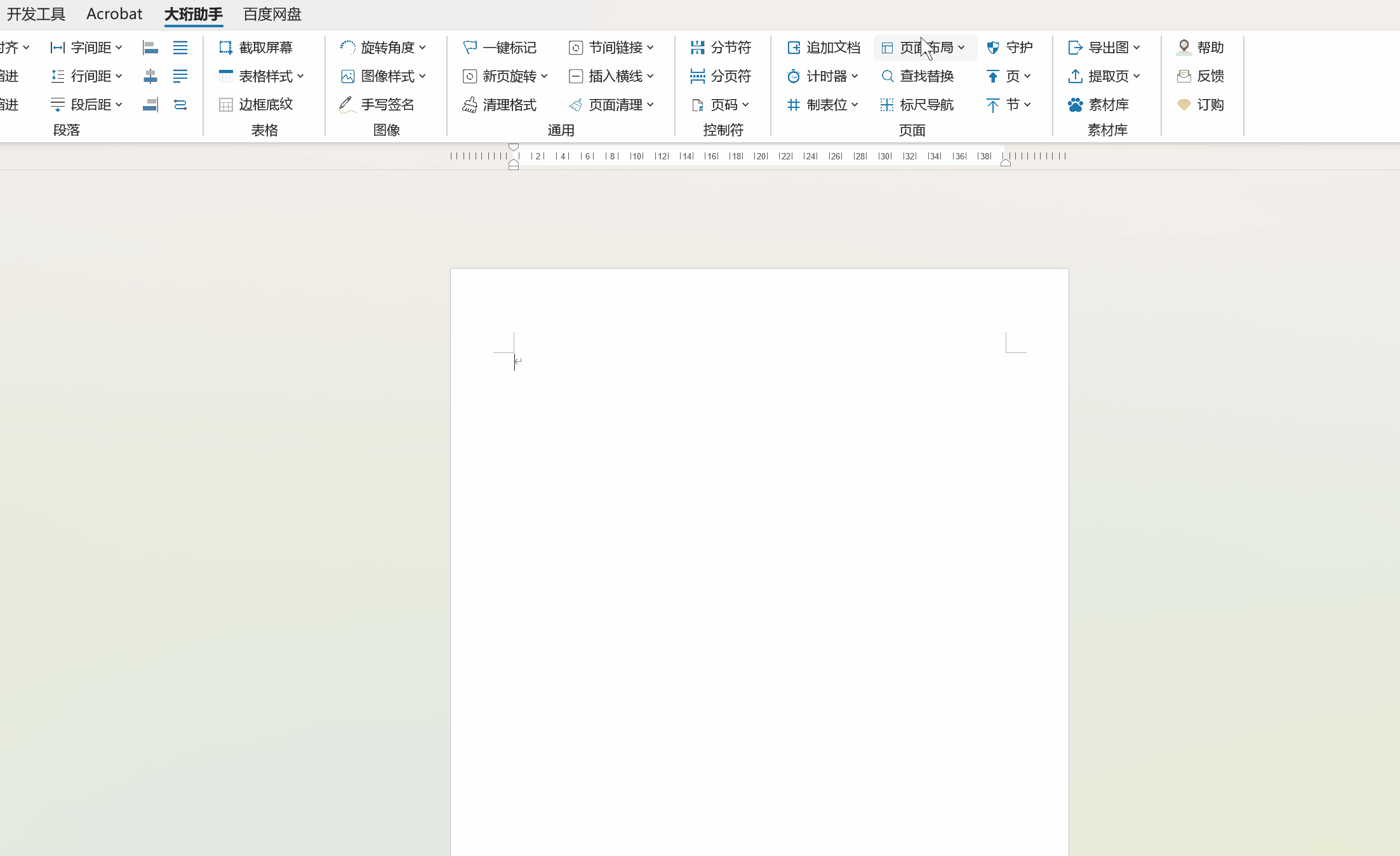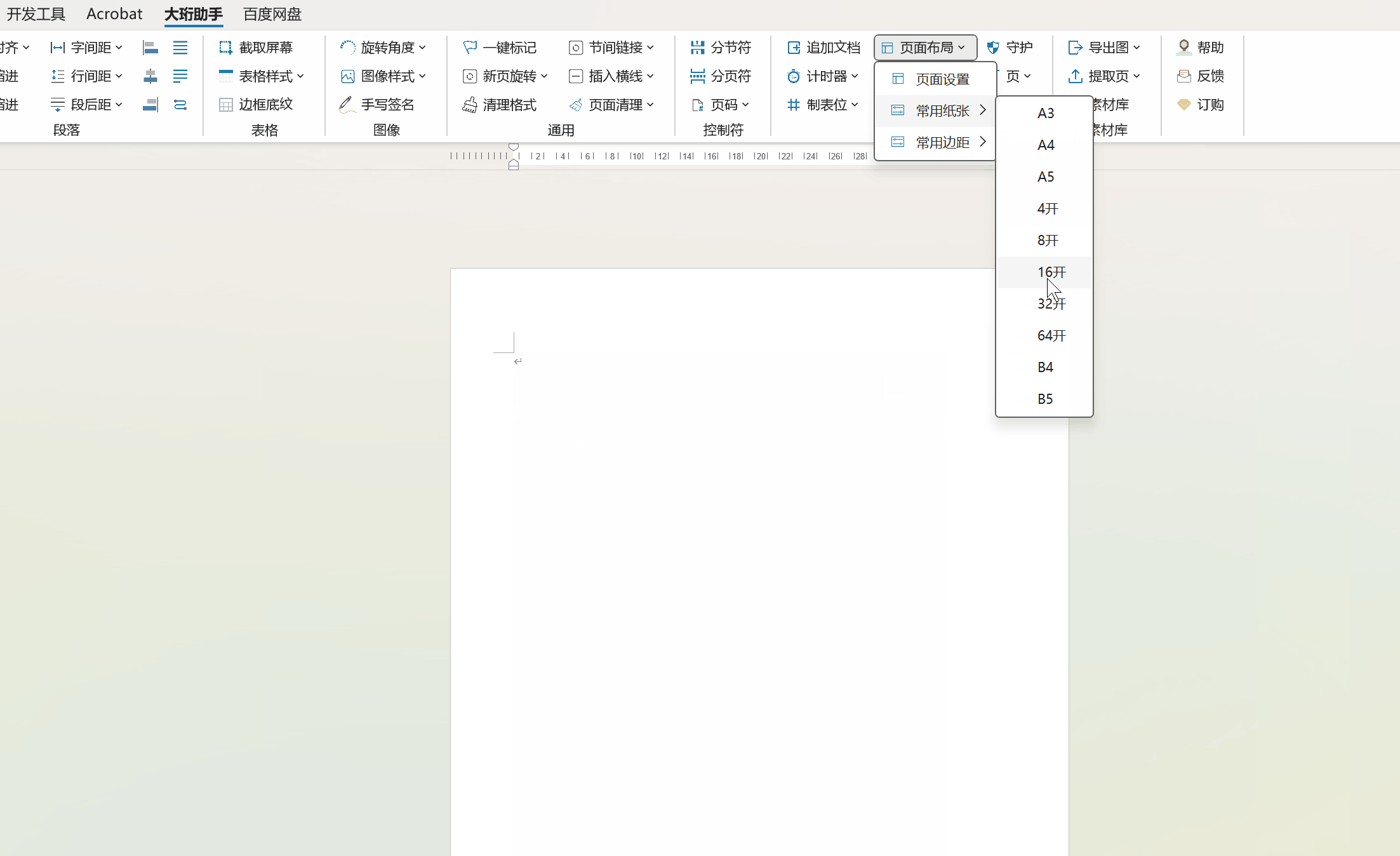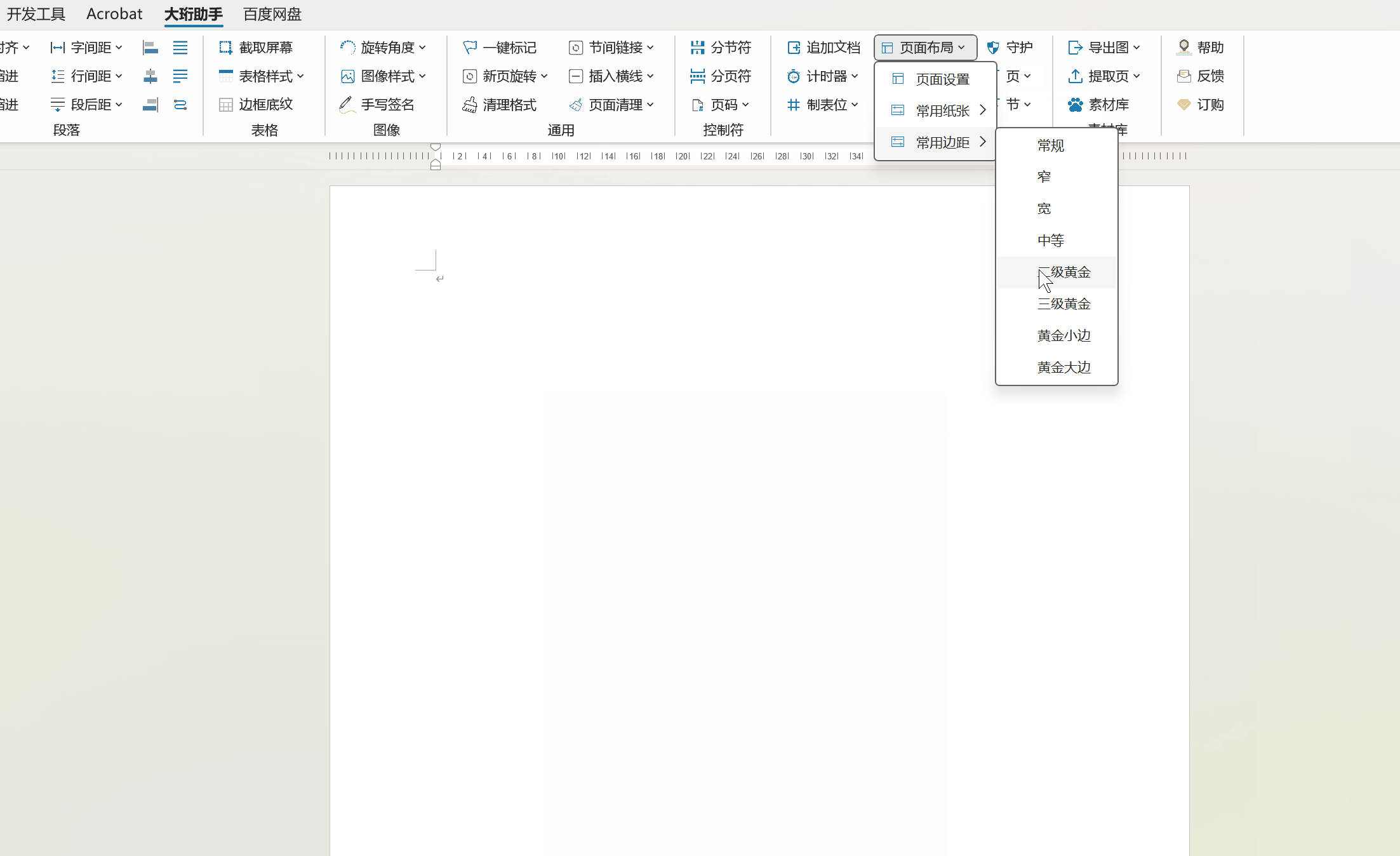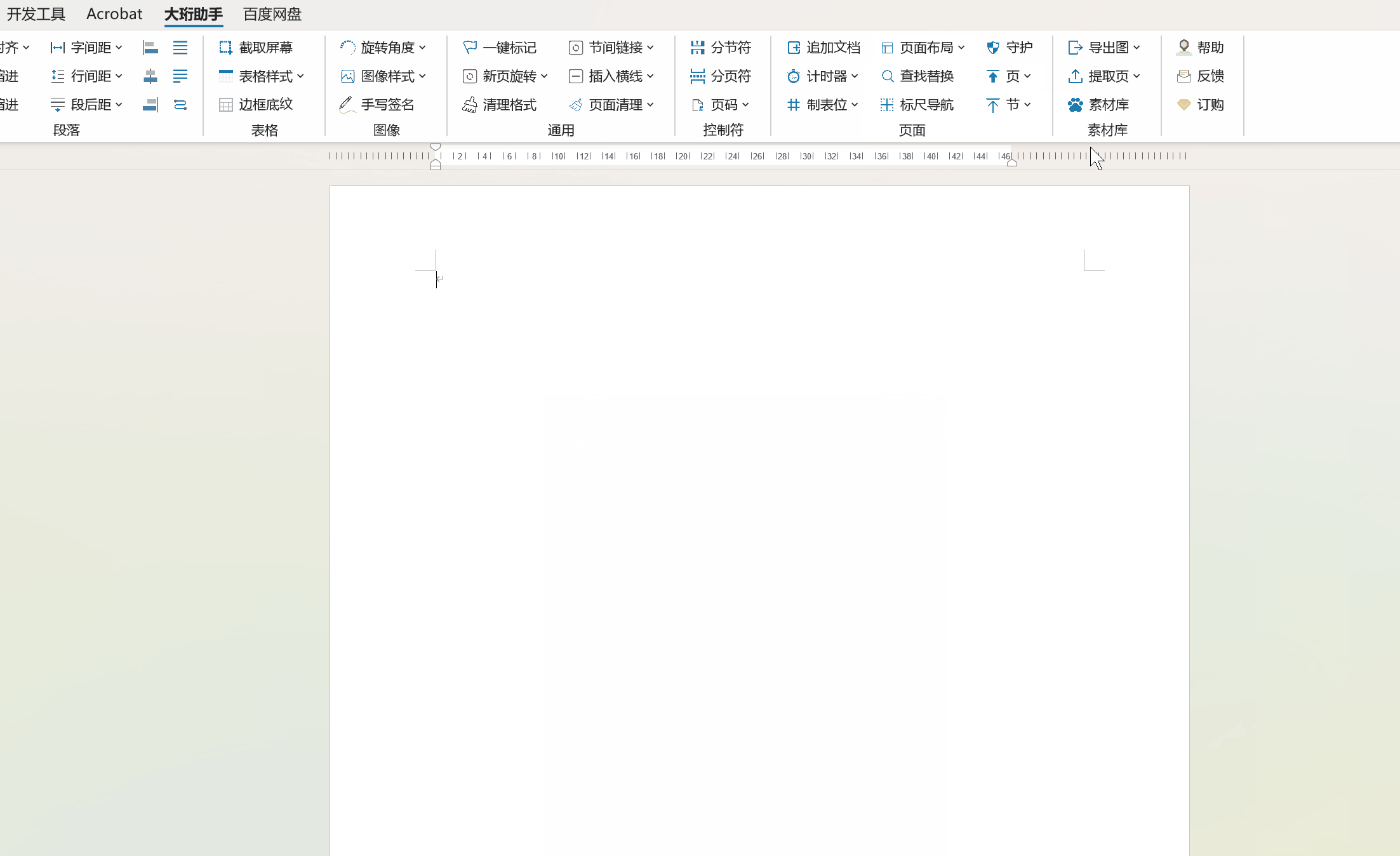
一键设置常用纸张和页面边距-Word插件-大珩助手
Word大珩助手是一款功能丰富的Office Word插件,旨在提高用户在处理文档时的效率。它具有多种实用的功能,能够帮助用户轻松修改、优化和管理Word文件,从而打造出专业而精美的文档。 【新功能】常用纸张和常用边距 1、一键设定符合中国人常用…...
在树莓派3B+中下载opencv(遇到的各种问题及解决)
目录 前言 1、删除原版本下新版本 2、python虚拟环境 3、python版本共存换链接——给版本降低 4、烧录之前版本的文件(在清华源中可以找,不用官网的烧录文件就行; 比如:(balenaEtcher)重新烧录有问题…...

精准检测,安全无忧:安全阀检测实践指南
安全阀作为一种重要的安全装置,在各类工业系统和设备中发挥着举足轻重的作用。 它通过自动控制内部压力,有效防止因压力过高而引发的设备损坏和事故风险,因此,对安全阀进行定期检测,确保其性能完好、工作可靠…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
