排序算法集合
1. 冒泡排序
排序的过程分为多趟,在每一趟中,从前向后遍历数组的无序部分,通过交换相邻两数位置的方式,将无序元素中最大的元素移动到无序部分的末尾(第一趟中,将最大的元素移动到数组倒数第一的位置;第二趟中,将第二大的元素移动到数组倒数第二的位置,以此类推)。
每排一趟,数组末尾的有序序列就向前增长一个元素,数组前端的无序部分就减少一个元素。
优化:某趟中,一次交换也没有发生,说明数组已有序,直接结束排序。
整个排序的过程中,剩余无序元素中最大的元素就像气泡一样不断“上浮”到数组末尾,所以该算法被称作冒泡排序。
冒泡排序的思想很简单,类似于递归:
要实现整个数组(n个元素)的有序,可以将数组分为前(n-1)个元素和最后一个元素。
首先确保最后一个元素有序(最大),然后再用相同的方式解决前(n-1)个元素组成的数组的有序性问题。
当然,你也可以当我上面这段话是放屁,因为冒泡排序的算法太过简单,按上面的方式来理解确实小题大做。
但伴随着简单算法的往往是极高的开销,这也使得冒泡排序没有任何的实际意义,仅作教学作用。
可以说冒泡排序是最拉的排序算法,接下来讲到的所有排序算法,效率都至少为其的十倍以上(实测结果非理论分析,理论分析出的时间复杂度几乎相同)
时间复杂度:最坏情况(元素逆序),最好情况(已有序)
空间复杂度:
//冒泡排序
void BubbleSort(int* arr, int len)
{for (int i = 0; i < len; i++){int flag = 1;for (int j = 0; j < len - 1 - i; j++){if (arr[j] > arr[j + 1]){flag = 0;swap(&arr[j], &arr[j + 1]);}}if (flag)return;}
}2. 选择排序
顾名思义,就是在每趟排序中,直接选出最大的元素(的下标),然后将其与无序部分末尾的元素进行交换,同时无序部分的末尾向前缩短一个元素。
相对于冒泡排序,二者的做法很像,但选择排序省去了交换相邻元素的过程(效率提高的关键),手段更加直接。
优化:在选出最大元素的同时,将最小元素也选出来,两端同时排序。
void SelectSort(int* arr, int len)
{int begin = 0, end = len - 1;while (begin < end){int max = begin;int min = begin;for (int i = begin + 1; i <= end; i++){if (arr[i] < arr[min])min = i;if (arr[i] > arr[max])max = i;}swap(&arr[begin], &arr[min]);swap(&arr[end], &arr[max]);begin++;end--;}
}但是,直接进行优化之后的算法会存在一个小bug:
假设在每趟排序中,将最大元素和最小元素选出来之后,先让最小元素交换到无序部分的前端,再让最大元素交换到无序部分末尾。
那么,当最大元素刚好在无序部分前端时,就会发生如下的过程:
1. 首元素(最大元素)与最小元素交换
2. 最大元素(首元素,此时该位置为最小元素)与末尾元素交换
 可以按照下面的方式解决。
可以按照下面的方式解决。
//选择排序
void SelectSort(int* arr, int len)
{int begin = 0, end = len - 1;while (begin < end){int max = begin;int min = begin;for (int i = begin + 1; i <= end; i++){if (arr[i] < arr[min])min = i;if (arr[i] > arr[max])max = i;}swap(&arr[begin], &arr[min]);if (begin == max)swap(&arr[end], &arr[min]);elseswap(&arr[end], &arr[max]);begin++;end--;}
}时间复杂度:
空间复杂度:
由于选择排序无法提前结束,所以其时间复杂度为稳定的。
但是,相比于冒泡排序,选择排序在整体上减少了频繁交换的消耗,在一般情况下,效率要远好于冒泡排序。
3. 插入排序
上面的两种算法是在为某个位置选择合适的元素填入,而插入排序则是在为某个元素选择合适的位置去存放,也正是这一差别,使其成为了这三位难兄难弟的老大哥。
为某个元素选择合适的位置,必然只有在其他元素都有序的情况下才能做到(或者局部有序)。
尽管数组在整体上无序,我们却可以将开头的一个元素看作是无序,接着将第二个元素插入其中。
于是,前两个元素就变得有序了,我们又可以将第三个元素插入其中……以此类推,数组便逐渐有序了。
插入排序,就是将数组分为两个部分:数组前端的有序部分(开始只有一个元素),和数组后半段的无序部分。然后将无序部分的元素逐个插入到有序部分。
而对于插入,我们采用的办法是:
从后向前遍历有序部分,如果当前位置的元素比要插入的元素大,则将当前位置的元素向后移动一个元素(为要插入的元素腾位置);如果当前位置的元素要比插入的元素小,则将要插入的元素插入到当前位置的后面(自己原本的位置,或者是第一种情况腾出来的位置)。
优化: 可优化为希尔排序,详见下文。
//插入排序
void InsertSort(int* arr, int len)
{for (int i = 1; i < len; i++){int temp = arr[i];int j = i;while(j > 0 && arr[j - 1] > temp){arr[j] = arr[j - 1];j--;}arr[j] = temp;}
}时间复杂度:最坏情况(元素逆序),最好情况(已有序)
空间复杂度:
虽然看上去与冒泡排序一模一样,但是其实际的消耗要小得多,相比于选择排序也要更优。
4. 希尔排序
在插入排序算法中,越小的元素越早插入越好,越大的元素越晚插入越好。
当元素恰好逆置时,算法的消耗较大,几乎等价于冒泡排序。
而希尔排序就是希尔为解决插入排序痛点而设计的算法,解决这一痛点的方法就是,先对整个数组进行跨度较大的粗调,再进行更加细致的调整(只有数据量较大时希尔排序的优化才有意义,否则直接使用插入排序即可)。
我们发现,如果较大的元素插入得较早,之后就会进行大量的操作将该元素后移,并且每次只移动一个元素。
如果我们能够快速地(一次跳过多个元素)将这些较大的元素调整到靠后的位置,使得数组基本有序,插入排序的时间复杂度就会无限接近于最好情况。
那么如何进行粗调呢?
1. 将数组的元素分为若干组(记组数为gap),每一组元素的下标模上gap所得的值相同(即每一组元素的下标为模gap的同余关系,类似于分层抽样)。
2. 对每一组的元素进行插入排序(这样一来,较大的元素每次向后移动的元素个数为gap,粗调的效率就远高于直接插入排序)。
3. 缩小gap的值,重复上述过程(一般做法为gap=gap/3+1,+1的目的是使得最后一趟排序时gap为1,也就是对整个数组进行一次插入排序)。
//希尔排序(插入排序优化)
void ShellSort(int* arr, int len)
{int gap = len;while (gap > 1){gap = gap / 3 + 1;for (int group = 0; group < gap; group++){for (int i = group + gap; i < len; i += gap){int temp = arr[i];int j = i;while (j > group && arr[j - gap] > temp){arr[j] = arr[j - gap];j -= gap;}arr[j] = temp;}}}
}可以看到,最内层的两层循环其实就是将插入排序中的“1”替换为了“gap”,将起点从“0+1”改成了“group + gap”。
控制group的循环就是在切换插入排序的组别。
优化:如果觉得四层循环看起来很唬人的话,我们也可以优化掉一层循环(但效率不变)
//希尔排序X(各组同时排,优化掉三重循环,但效率相同)
void ShellSort_X(int* arr, int len)
{int gap = len;while (gap > 1){gap = gap / 3 + 1;for (int i = gap; i < len; i++){int temp = arr[i];int j = i;while (j > 0 && arr[j - gap] > temp){arr[j] = arr[j - gap];j -= gap;}arr[j] = temp;}}
}时间复杂度:平均情况,最好情况
空间复杂度:
初见希尔排序的代码,可能会误以为其效率极低,但实际上希尔排序的效率极高,甚至在数据量较大时,效率高出上文介绍的算法不止一个量级(百倍以上)!
接下来的几种算法,于希尔排序同属一个量级,但效率有略微差别。
其排序的过程极其复杂,具有许多不可控因素,不能简单地通过循环的层数来计算时间复杂度。
希尔排序的代码很难理解,但是其解决问题的思想却很值得我们学习借鉴。
5. 堆排序
详见这篇文章:全面详解堆-CSDN博客
6. 快速排序
详见这篇文章:C语言实现快速排序算法-CSDN博客
值得一提的是,快速排序正如其名,快且综合实力强。
C语言中,qsort函数的底层算法便是采用的快速排序算法。
7. 归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
若将两个有序表合并成一个有序表,称为二路归并。
以二路归并为例,假如一个数组从中间位置被分为了前后两个部分,而这两个部分都是有序的,那么我们就可以采用与合并两个有序链表相同的思路:比较两个序列中的最小值,将较小的那个插入到新的序列中,不断重复这样的操作,直到原序列中的值全部插入到新序列中。
但前提是,前后两个子序列都要有序。
所以我们的首要任务是使得前后两个子序列有序,而使其有序的方式依然如上。

于是我们找到的递归的思路:
void _MergeSort(int* arr, int* copy, int begin, int end)
{if (begin >= end)return;//区间不能分为[begin,mid-1]和[mid,end]int mid = (begin + end) / 2;_MergeSort(arr, copy, begin, mid);_MergeSort(arr, copy, mid + 1, end);//归并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int cur = begin;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){copy[cur++] = arr[begin1++];}else{copy[cur++] = arr[begin2++];}}while (begin1 <= end1) { copy[cur++] = arr[begin1++]; }while (begin2 <= end2) { copy[cur++] = arr[begin2++]; }memcpy(arr + begin, copy + begin, (end - begin + 1) * sizeof(int));
}//归并排序
//时间复杂度O(n*logn),空间复杂度O(n)
void MergeSort(int* arr, int len)
{int* copy = (int*)malloc(sizeof(int) * len);if (copy == NULL){perror("malloc fail");return;}_MergeSort(arr, copy, 0, len - 1);free(copy);
}和快速排序类似,既然这个算法是用递归的方式实现的,我们就会考虑其非递归的实现方式。
但与快速排序不同,快速排序的递归方式类似于二叉树的前序遍历,但是归并排序类似于后序遍历。
参考栈与递归的实现-CSDN博客会发现,二叉树前序遍历的非递归实现很简单,但是后序遍历的非递归实现则十分麻烦。
将递归算法转化为非递归算法,除了利用栈来模拟实现,也可以尝试直接利用迭代来实现。
思路就是将数组按gap个数据为一组分为多组,每两个相邻的组进行插入合并,随后gap变为原来的两倍,再次重复以上过程,直到gap大于数组长度。
当然,最后一组可能分配不到gap个数据,也可能只能分出奇数个组,针对这些问题,进行插入合并(归并)的代码进行了调整。
//归并排序非递归
void MergeSortNonR(int* arr, int len)
{int* copy = (int*)malloc(sizeof(int) * len);if (copy == NULL){perror("malloc fail");return;}for (int gap = 1; gap < len; gap *= 2){for (int i = 0; i < len; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//第二组都越界,不归并了if (begin2 >= len){break;}//第二组越界部分,修正并归并if (end2 >= len){end2 = len - 1;}int cur = i;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){copy[cur++] = arr[begin1++];}else{copy[cur++] = arr[begin2++];}}while (begin1 <= end1) { copy[cur++] = arr[begin1++]; }while (begin2 <= end2) { copy[cur++] = arr[begin2++]; }memcpy(arr + i, copy + i, ((end2 - i + 1) * sizeof(int)));}}free(copy);
}时间复杂度:
空间复杂度:
相关文章:
排序算法集合
1. 冒泡排序 排序的过程分为多趟,在每一趟中,从前向后遍历数组的无序部分,通过交换相邻两数位置的方式,将无序元素中最大的元素移动到无序部分的末尾(第一趟中,将最大的元素移动到数组倒数第一的位置&…...
pdf文件太大如何变小,苹果电脑压缩pdf文件大小工具软件
压缩PDF文件是我们在日常办公和学习中经常会遇到的需求。PDF文件由于其跨平台、保持格式不变的特点,被广泛应用于各种场合。然而,有时候我们收到的PDF文件可能过大,不便于传输和存储,这时候就需要对PDF文件进行压缩。下面…...

vite项目打包,内存溢出
解决方案: "build1": "node --max-old-space-size8096 ./node_modules/vite/bin/vite.js build", 人工智能学习网站 https://chat.xutongbao.top...

Matlab解决施密特正交规范化矩阵(代码开源)
#最近在学习matlab,刚好和线代论文重合了 于是心血来潮用matlab建了一个模型来解决施密特正交规范化矩阵。 我们知道这个正交化矩阵挺公式化的,一般公式化的内容我们都可以用计算机来进行操作,节约我们人工的时间。 我们首先把矩阵导入进去…...

自养号测评助力:如何打造沃尔玛爆款?
沃尔玛,作为全球零售业的领军者,其平台为卖家们提供了一个巨大的商业舞台。然而,在这个竞争激烈的舞台上,如何迅速且有效地提升销量,成为了卖家们必须面对的重大挑战。 在探讨沃尔玛平台销量提升的策略时,我…...

C语言编译与链接
C语言编译与链接 目录 C语言编译与链接 一、概述 二、编译过程 三、链接过程...

电子电器架构 --- 智能座舱技术分类
电子电器架构 — 智能座舱技术分类 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,…...

提供操作日志、审计日志解决方案思路
操作日志 现在大部分公司一般使用SpringCloud这条技术栈,操作日志通过网关Gateway提供的Globalfilter统一拦截请求解析请求是比较好的选选择。 优点:相对于传统的过滤器、拦截器同步阻塞方案,SpringCloud Gateway使用的Webflux中的reactor-…...
选择富唯智能的可重构装配系统,就是选择了一个可靠的合作伙伴
在数字化、智能化的浪潮中,制造业正迎来一场前所未有的变革。而在这场变革中,富唯智能凭借其卓越的技术实力和创新能力,成为引领行业发展的领军企业。选择富唯智能的可重构装配系统,就是选择了一个可靠的合作伙伴,共同…...

echarts tooltip太多显示问题解决方案
思路:设置5个一换行 tooltip: {trigger: axis,confine:true,//限制tooltip在图表范围内展示// extraCssText: max-height:60%;overflow-y:scroll,//最大高度以及超出处理extraCssText: max-height:60%;overflow-y:scroll;white-space: normal;word-break: break-al…...
【control_manager】无法加载,gazebo_ros2_control 0.4.8,机械臂乱飞
删除URDF和SDRF文件中的特殊注释#, !,: xacro文件解析为字符串时出现报错 一开始疯狂报错Waiting for /controller_manager node to exist 1717585645.4673686 [spawner-2] [INFO] [1717585645.467015300] [spawner_joint_state_broadcaster]: Waiting for /con…...

深入对比:Transformer与LSTM的详细解析
在深度学习和自然语言处理(NLP)领域,Transformer和长短时记忆网络(LSTM)是两个备受瞩目的模型。它们各自拥有独特的优势,并在不同的任务中发挥着重要作用。本文将对这两种模型进行详细对比,帮助…...

lsof 命令
lsof(list open files)是一个列出当前系统打开文件的工具。在linux环境下,任何事物都以文件的形式存在,通过文件不仅仅可以访问常规数据,还可以访问网络连接和硬件。所以如传输控制协议 (TCP) 和用户数据报协议 (UDP) …...
F5G城市光网,助力“一网通城”筑基数字中国
《淮南子》中说,“临河而羡鱼,不如归家织网”。 这句话在后世比喻为做任何事情都需要提前做好准备,有了合适的工具,牢固的基础,各种难题也会迎刃而解。 如今,数字中国发展建设如火如荼,各项任务…...
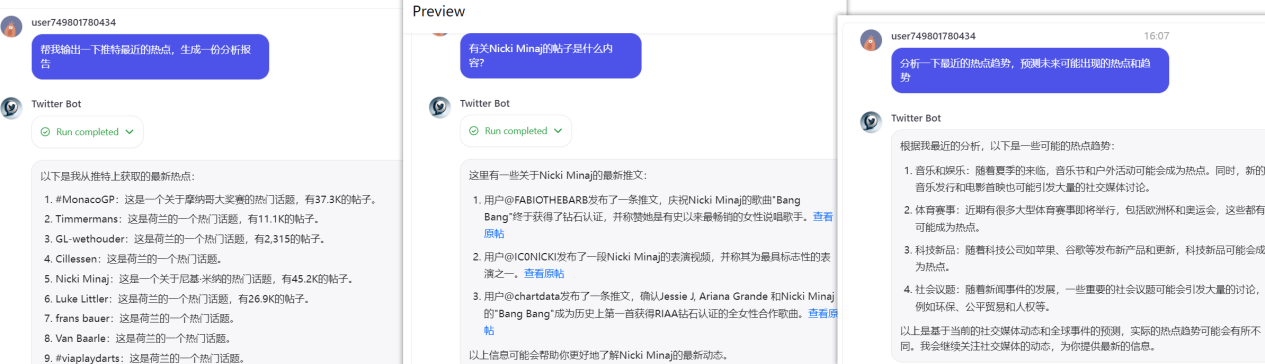
Ownips+Coze海外社媒数据分析实战指南
目录 一、引言二、ISP代理简介三、应用实践——基于Ownips和coze的社媒智能分析助手3.1、Twitter趋势数据采集3.1.1、Twitter趋势数据接口分析3.1.2、Ownips原生住宅ISP选取与配置3.1.3、数据采集 3.2、基于Ownips和Coze的社媒智能助手3.2.1、Ownips数据采集插件集成3.2.2、创建…...
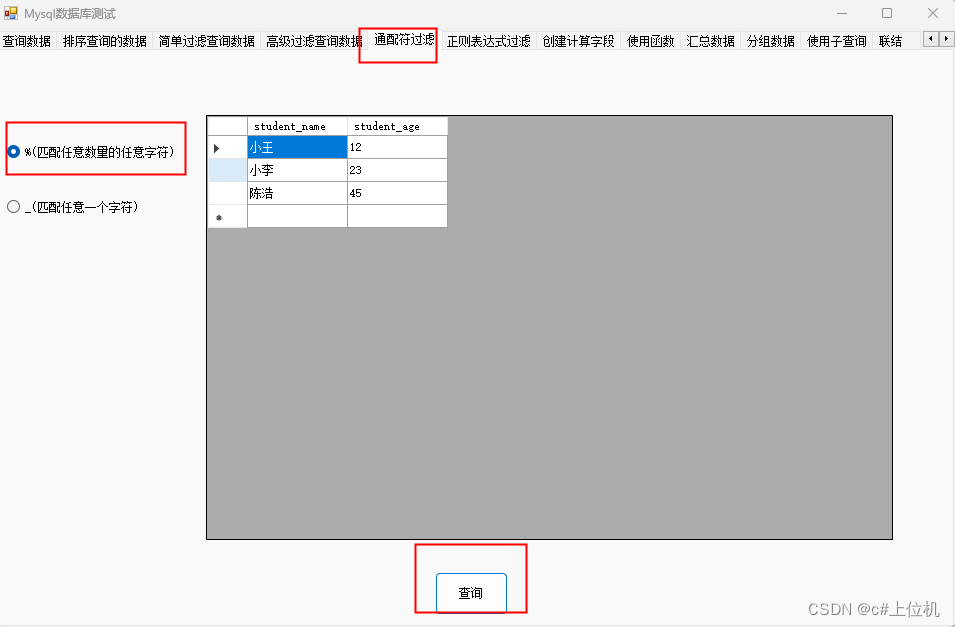
C#操作MySQL从入门到精通(10)——对查询数据进行通配符过滤
前言 我们有时候需要查询数据,并且这个数据包含某个字符串,这时候我们再使用where就无法实现了,所以mysql中提供了一种模糊查询机制,通过Like关键字来实现,下面进行详细介绍: 本次查询的表中数据如下: 1、使用(%)通配符 %通配符的作用是,表示任意字符出现任意次数…...
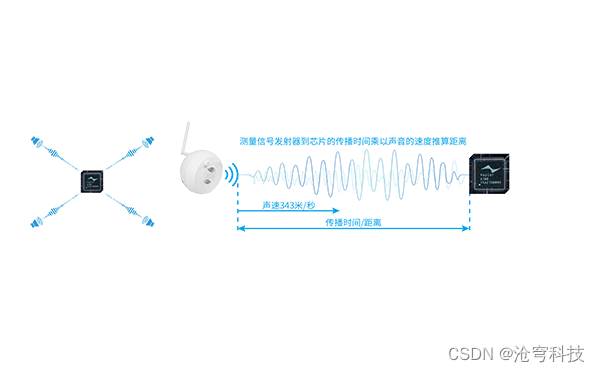
厘米级精确定位,开启定位技术新时代
定位技术在当前这个科技发展时代可以说是以以前所未有的速度在发展,其中厘米级精确定位技术更是成为当前的研究热点和实际应用中的佼佼者。这项技术以其高度的精准性和广泛的应用前景,正在逐渐改变我们的生活和工作方式。接下来我们跟着深圳沧穹科技一起…...
docker 存储 网络 命令
文章目录 1 docker存储1.1 目录挂载2.1卷映射2.1.1卷映射和目录挂载的区别2.1.2卷映射的使用 2 docker网络2.1查看docker的默认网络2.2查看容器的IP2.3容器互通2.4自定义网络2.4.1 创建自定义网络2.4.2创建容器的时候加入到自定义的网络2.4.3使用域名进行容器之间的访问2.4.4re…...
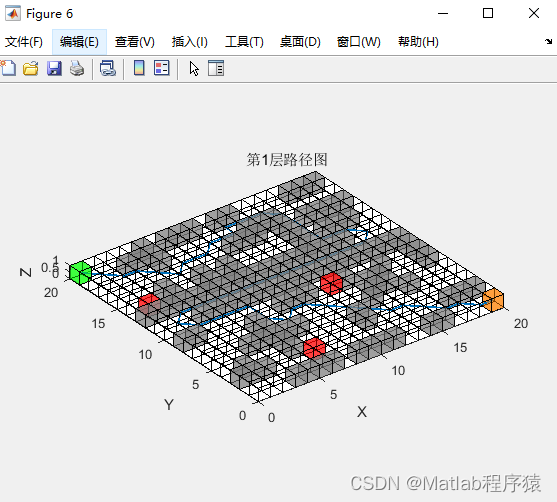
【MATLAB源码-第222期】基于matlab的改进蚁群算法三维栅格地图路径规划,加入精英蚁群策略。包括起点终点,障碍物,着火点,楼梯。
操作环境: MATLAB 2022a 1、算法描述 蚁群算法(Ant Colony Optimization,ACO)是一种通过模拟蚂蚁觅食行为的启发式优化算法。它由意大利学者Marco Dorigo在20世纪90年代初提出,最初用于解决旅行商问题(T…...
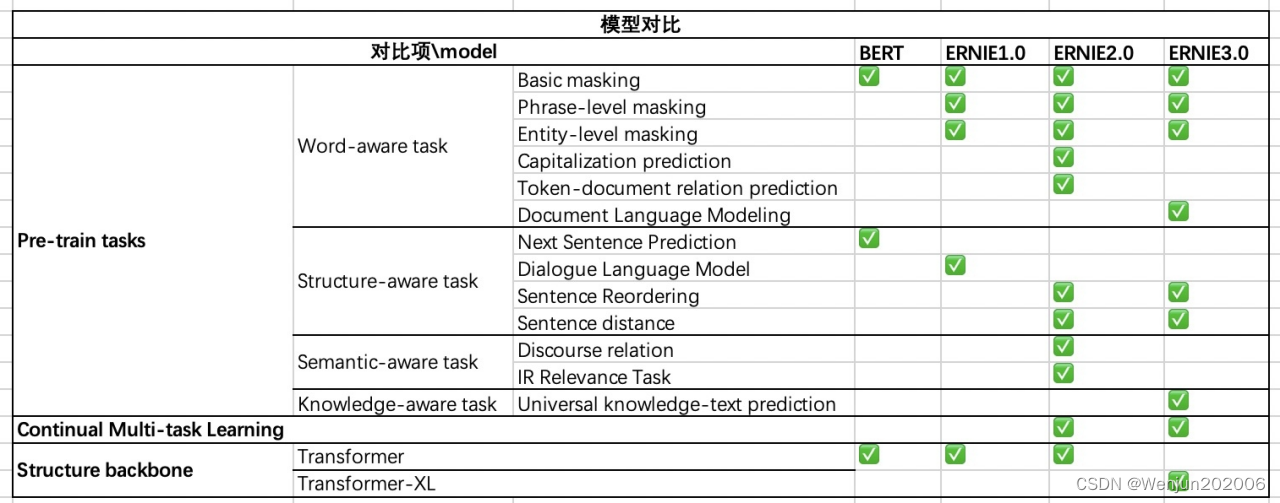
百度ERNIE系列预训练语言模型浅析(4)-总结篇
总结:ERNIE 3.0与ERNIE 2.0比较 (1)相同点: 采用连续学习 采用了多个语义层级的预训练任务 (2)不同点: ERNIE 3.0 Transformer-XL Encoder(自回归自编码), ERNIE 2.0 Transformer Encode…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
