Codeforces Round 854 by cybercats (Div. 1 + Div. 2) C、D1
C. Double Lexicographically Minimum
题意
字符串sss,你可以把它按任意顺序组合,保留的是你组合的字符串和它的倒序之间大的那一个,问你在满足上面条件的前提下字典序最小的字符串。
思路
分析不难发现在没达到一个关键的点的时候肯定是对称是最好的,这样肯定能保证得到的字符串是最小的,而关键点到了之后就不需要平分了,全部放前面就好了。那关键点要怎么看,其实也很明显,因为判断字符串大小主要看第一个不同的字符,所以只要把第一个奇数个数的字符的最后一个放到后面就行了。那为什么是奇数呢?因为如果是偶数那要满足题目要求,后面就必须要比前面多放两个,但这样就比正常情况下大了(这里可以画图模拟一下就行)。
最后就是如果关键点后面只有一种类型的字符那就需要特判一下,才能满足题目要求,这里就看一下代码画图模拟一下把,也好理解。
代码
#include <bits/stdc++.h>using namespace std; const int N = 105;int st[30];void solve()
{string s;cin >> s;memset(st, 0, sizeof(st)); // 记录a, b, ..., z各有多少个for (int i = 0; i < s.size(); i ++ ) st[s[i] - 'a'] ++;string l = "", r = "";for (int i = 0; i < 26; i ++ ) // 不到关键点就前后分开{while (st[i] > 1) {l += (char)('a' + i);r += (char)('a' + i);st[i] -= 2;}if(st[i]) break; // 奇数就代表找到了,可以中断了}int cc = 0;for(int i = 0; i < 26; i ++) if(st[i]) cc ++; // 判断一下关键点后面有几个字符if(cc <= 2) {for (int i = 25; i >= 0; i -- ) // 把大的放前面{while (st[i] > 1) {l += (char)('a' + i);r += (char)('a' + i);st[i] -= 2;}if(st[i]) l += (char)('a' + i);}}else {int flag = true;for(int i = 0; i < 26; i ++) {while(st[i]) {if(flag) // 把关键点放到后面r += (char)('a' + i), st[i] --, flag = 0; else // 剩下的全放前面l += (char)('a' + i), st[i] --;}}}reverse(r.begin(), r.end()); // 翻转一下cout << l << r << '\n';
}int main()
{int T = 1;cin >> T;while (T --) {solve(); }return 0;
}
D1. Hot Start Up (easy version)
题意
nnn个数,大小为kkk的数组coldcoldcold,hothothot,你有两个CPU,如果你选择的CPU的上一个进程和当前的进程一样,所用时间就是hothothot,否则coldcoldcold。问你完成所有的进程的最短时间。
思路
很明显是一个动态规划问题,关键是动态规划数组代表的含义,这里是dp(i,j,k)dp(i, j, k)dp(i,j,k),代表走到 iii 的时候CPU1最后处理的进程是 jjj, CPU2最后处理的进程是 kkk。但这样肯定是要超时的,然后通过题目可以得到要去进行 iii,i−1i - 1i−1 必须要完成,所以可以优化一维,这样就可以了。
dp[i][j]dp[i][j]dp[i][j]就代表进程处理到第 iii 个位置的时候,CPU1最后处理的进程是 jjj(CPU2默认为 a[i−1]a[i - 1]a[i−1])这样就题目要求得到了转换方程:
代码
#include <bits/stdc++.h>using namespace std;#define int long long // 开一下 long long
typedef long long LL;
const int N = 5e5 + 10, mod = 998244353;void solve()
{int n, k;cin >> n >> k;vector<int> a(n + 1), cold(k + 1), hot(k + 1);for (int i = 1; i <= n; i ++ ) cin >> a[i];for (int i = 1; i <= k; i ++ ) cin >> cold[i];for (int i = 1; i <= k; i ++ ) cin >> hot[i];vector<vector<int>> dp(n + 1, vector<int>(k + 1, 1e18)); // 初始化dp[1][0] = cold[a[1]];for (int i = 2; i <= n; i ++ ){for (int j = 0; j <= k; j ++ ){int x = cold[a[i]];if (a[i - 1] == a[i]) x = hot[a[i]];// 转化方程dp[i][j] = min(dp[i][j], dp[i - 1][j] + x);dp[i][a[i - 1]] = min(dp[i][a[i - 1]], dp[i - 1][j] + (a[i] == j ? hot[a[i]] : cold[a[i]]));}}int ans = 1e18;for (int i = 0; i <= k; i ++ ) ans = min(ans, dp[n][i]);cout << ans << '\n';
}signed main()
{int T = 1;cin >> T;while (T -- ){solve();}return 0;
}
反思
做 C 题的时候把自己绕晕了,之间明白是这样做的,但是做起来不是这里不行就哪里不行,做题之前需要把自己的思路逻辑理清楚,然后再去写。
D 题就是自己动态规划做题经验不足了,状态表示没有想到,还需要继续做题。
相关文章:
 C、D1)
Codeforces Round 854 by cybercats (Div. 1 + Div. 2) C、D1
C. Double Lexicographically Minimum 题意 字符串sss,你可以把它按任意顺序组合,保留的是你组合的字符串和它的倒序之间大的那一个,问你在满足上面条件的前提下字典序最小的字符串。 思路 分析不难发现在没达到一个关键的点的时候肯定是…...

API 网关日志的价值,你了解多少?
本文介绍了 API 网关日志的价值,并以知名网关 Apache APISIX 为例,展示如何集成 API 网关日志。 作者钱勇,API7.ai 技术工程师,Apache APISIX Committer。 原文链接 网关日志的价值 在数字化时代,软件架构随着业务成…...
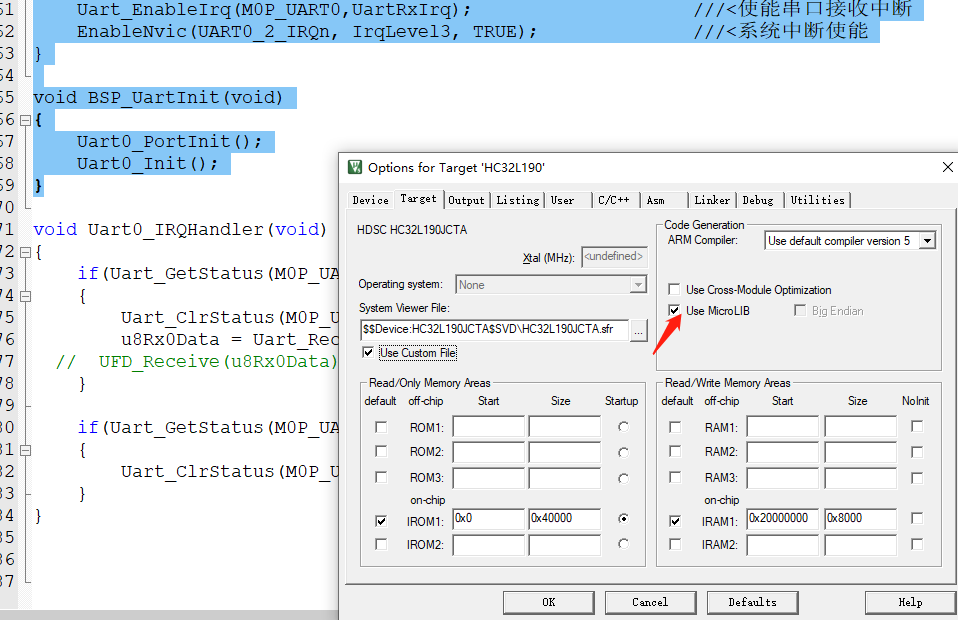
华大单片机、STM32单片机如何做printf串口打印格式化输出
第一种方法:使用标准C库,但使用标准C库你必须关闭半主机模式(1)添加下面代码就是关闭半主机模式/* 告知连接器不从C库链接使用半主机的函数 */ #pragma import(__use_no_semihosting)/* 定义 _sys_exit() 以避免使用半主机模式 */…...
unity 面试汇总
1、什么是协同程序?答:在主线程运行时同时开启另一段逻辑处理,来协助当前程序的执行。换句话说,开启协程就是开启一个可以与程序并行的逻辑。可以用来控制运动、序列以及对象的行为。2、Unity3D中的碰撞器和触发器的区别ÿ…...
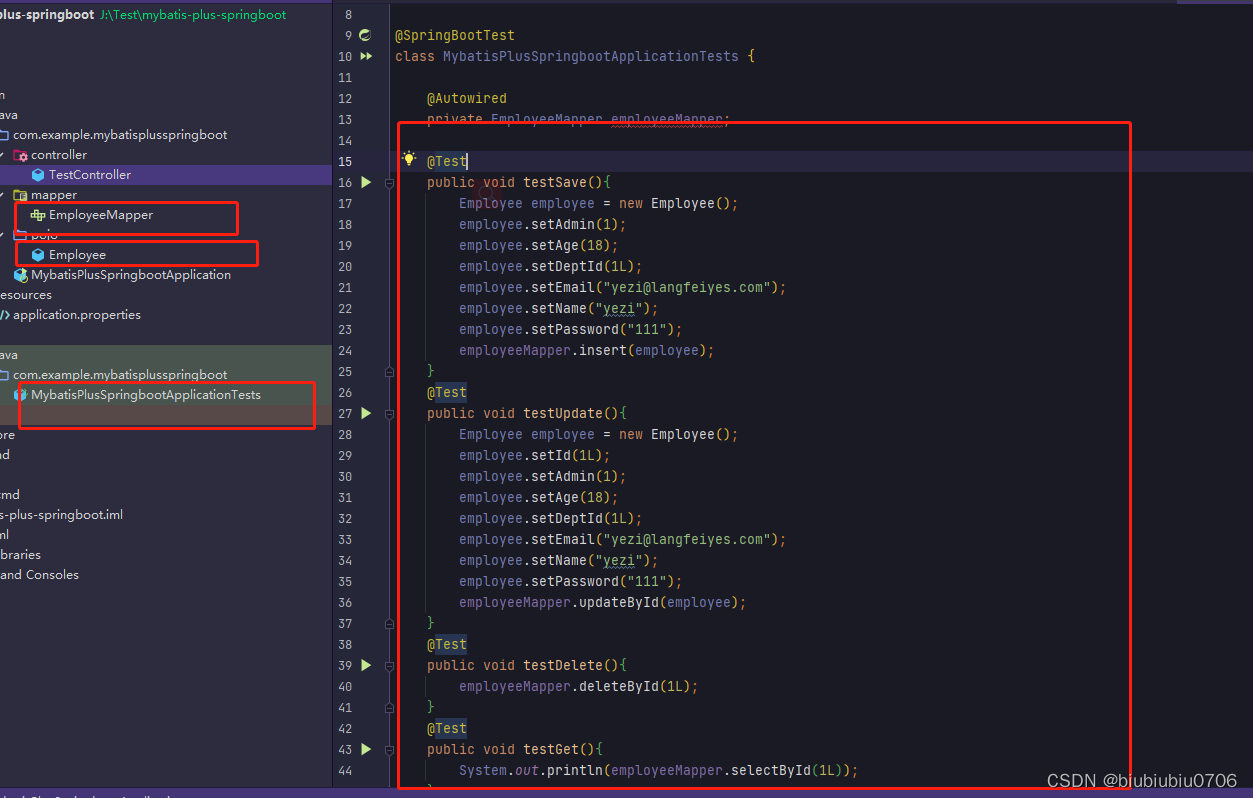
Spring SpringBoot中使用Mybatis-plusDemo1
官网:https://baomidou.com GitHub:GitHub - baomidou/mybatis-plus: An powerful enhanced toolkit of MyBatis for simplify development Gitee:mybatis-plus: mybatis 增强工具包,简化 CRUD 操作。 文档 http://baomidou.com低代码组件库 http://aizuda.com My…...
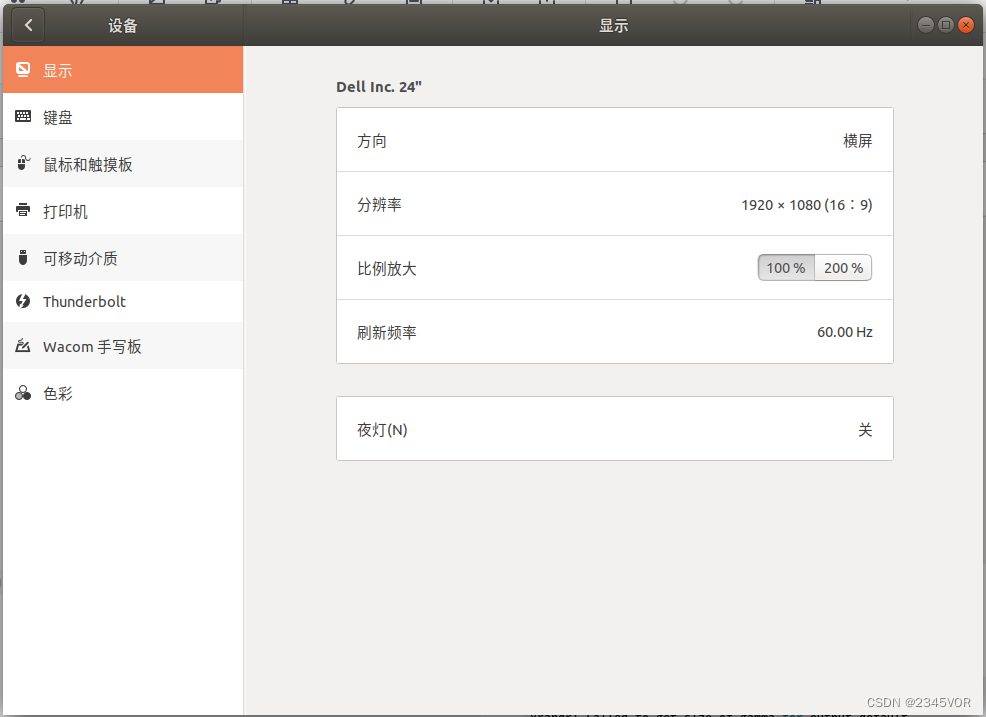
【18.04Ubuntu中解决无法识别显示屏】
【18.04Ubuntu中解决无法识别外接显示屏】1. 问题来源2. 检查Ubuntu是否识别出外接显示器3. 解决没有识别出外接显示器问题4. 显示器扩展屏幕设置1. 问题来源 实验室的一个dell显示器,通过HDMI连接电脑后,在Windows上连接上就直接可以使用了。由于我电脑…...
Python 协程详解,都在这里了
什么是协程 协程(co-routine,又称微线程、纤程) 是一种多方协同的工作方式。 协程不是进程或线程, 其执行过程类似于 Python 函数调用, Python 的 asyncio 模块实现的异步IO编程框架中, 协程是对使用 asy…...

百家号如何写文章赚钱,百家号写文章真的赚钱?
随着互联网的快速发展,越来越多的人开始关注到写文章赚钱这个领域。而在众多写作平台中,头条号无疑是最受欢迎的一个。那么,百家号写文章赚钱是真的吗?如何写文章赚钱呢?下面我们就来一一解答。 首先,百家号…...

【HDFS】datanodeReport RPC优化
cat datanodeReport.txt | awk ‘{print $8}’ | sort | uniq | wc -l 结果15,说明我们有15个router。 每15秒一个router8次调用这个rpc。15秒是我们的监控采集间隔。 看下router为什么要调用这个rpc。 顺着这个配置项去寻找:dfs.federation.router.dn-report.time-out 一…...
【数据结构】研究链表带环问题
💯💯💯💯 本篇主要研究的是链表带环问题,快慢指针的应用,分析不同解法对带环链表的处理,梳理完本篇你将对链表的理解更加透彻Ⅰ.研究链表带环问题Ⅱ.扩展带环问题1.为什么慢指针和快指针一定会相…...
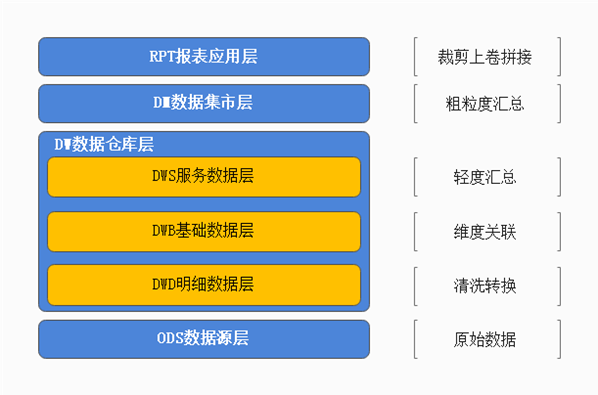
数据仓库的设计思想
数据仓库设计 知识点01:设计大纲与学习目标 #内容大纲1、数据仓库基础知识(回顾)什么是数仓为什么有数仓数仓的特点是什么OLTP和OLAP系统区别(数据库和数仓的区别)2、数仓系统的架构与核心流程核心1:ETL核…...

【JavaSE】数组的定义与使用详解
目录 1.数组的基本概念 1.1数组的好处 1.2什么是数组 1.3数组的定义及初始化 1.3.1数组的创建 1.3.2数组的初始化 1.4数组的使用 1.4.1访问数组中的元素 1.4.2遍历数组 2.数组的类型 2.1认识JVM的内存分布 2.2基本类型变量与引用类型变量 2.3认识null 3.数组的应…...
Kubernetes14:Helm为了部署像微服务这种的大型项目
Kubernetes14:Helm介绍(为了部署像微服务这种的大型项目) 1、Helm的引入 (1)之前方式部署应用基本过程 编写yaml文件 1、deployment kubectl create deployment nginx --imagenginx --dryrun -o yaml > nginx.yaml2、Service kubect…...

2.3操作系统-存储管理:页式存储、逻辑地址、物理地址、物理地址逻辑地址之间的地址关系、页面大小与页内地址长度的关系、缺页中断、内存淘汰规则
2.3操作系统-存储管理:页式存储、逻辑地址、物理地址、物理地址逻辑地址之间的地址关系、页面大小与页内地址长度的关系、缺页中断、内存淘汰规则页式存储逻辑地址、物理地址如何判断物理地址和逻辑地址它们之间的地址关系?页面大小与页内地址长度的关系…...
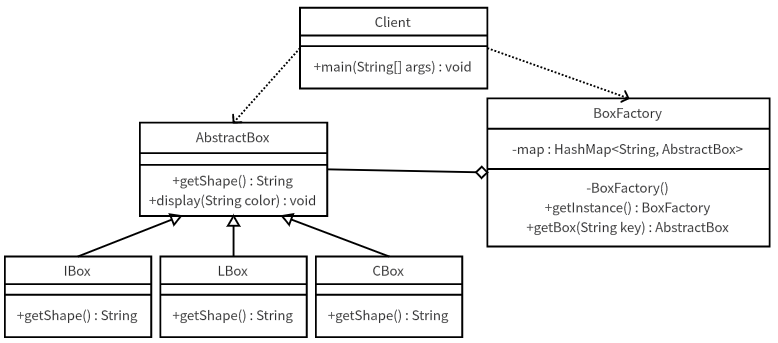
设计模式3——结构型模式
结构型模式描述如何将类或对象按某种布局组成更大的结构,它分为类结构型和对象结构型模式,前者采用继承机制来组织接口和类,后者采用组合或聚合来组合对象。 由于组合关系或聚合关系比继承关系耦合度低,满足“合成复用原则”&…...

css——图片缩放,拉伸,变形的解决办法
你的图片即将变得超级丝滑图片为什么会拉伸变形?怎么解决?css的object-fit属性object-fit属性有什么用介绍一下object-position举个小栗子图片为什么会拉伸变形? 前端布局时,图片会出现拉伸、缩放和变形的原因可能有多种: 1.例如图…...

【工具使用】STM32CubeMX-基础使用篇
一、概述 无论是新手还是大佬,基于STM32单片机的开发,使用STM32CubeMX都是可以极大提升开发效率的,并且其界面化的开发,也大大降低了新手对STM32单片机的开发门槛。 本文主要面向初次接触STM32CubeMX的同学,大…...
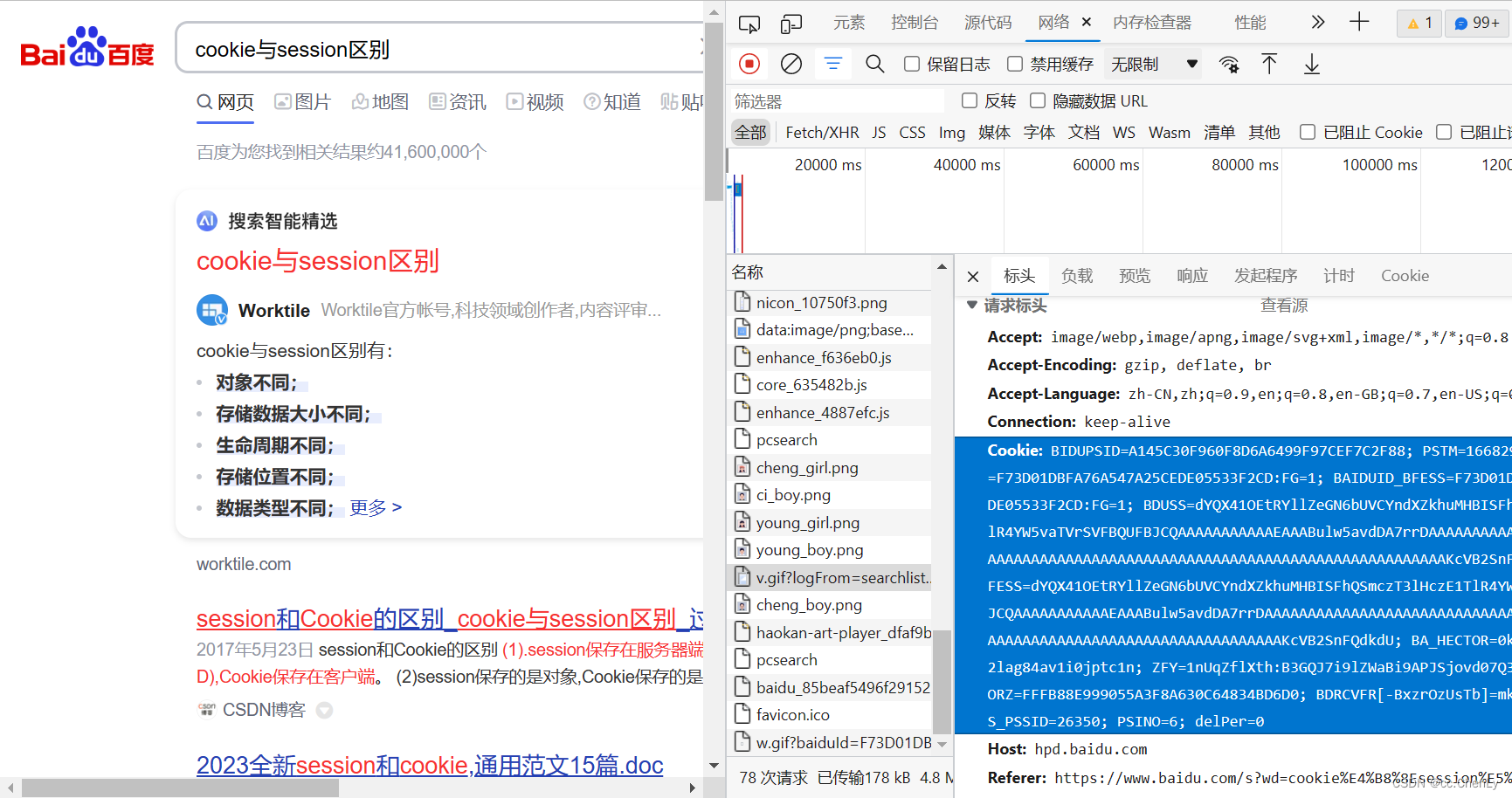
面试题解-理解cookie、session和token
项目vuespringboot 1、token 用户填写密码账号发送至后端,由后端生成token,返回给前端,前端把它存放起来,如放在cookie或者localStorage里面 前端向服务器发起请求时在请求头携带token,判断用户身份给与反应。 //后…...
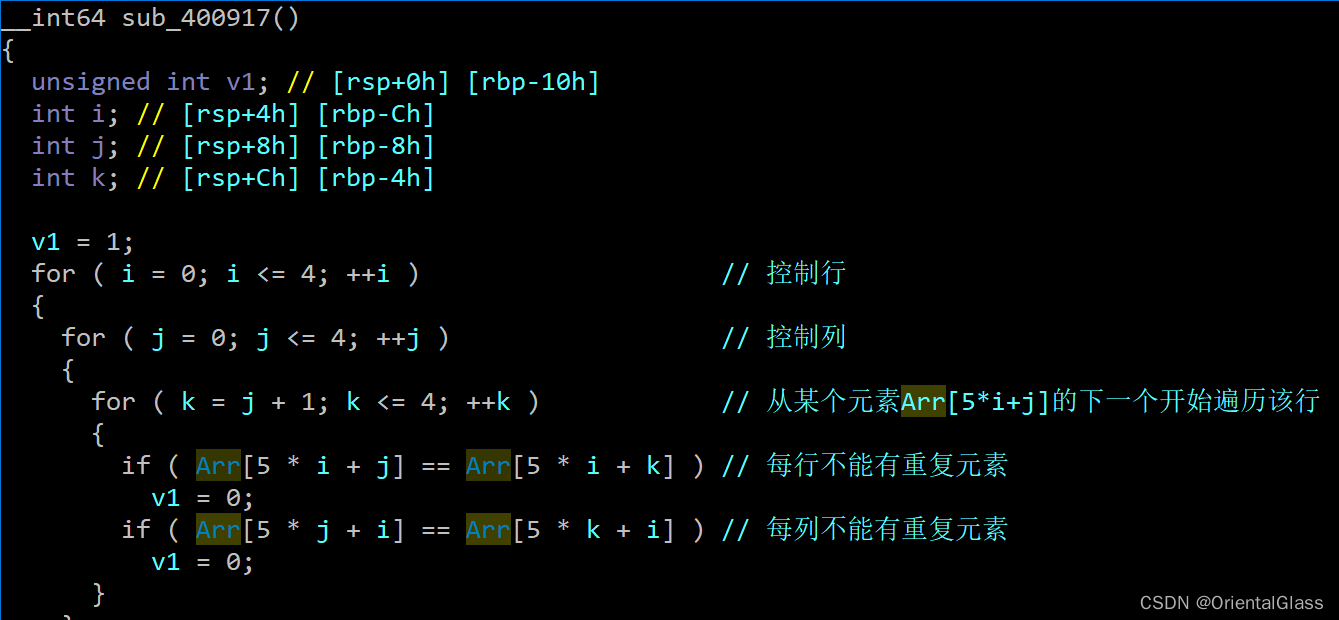
Buuctf [GUET-CTF2019]number_game 题解
目录 一.主函数逻辑 二.level_stor()函数 三.mid_stor函数 四.operate函数 五.judge2函数 六.求解flag 一.主函数逻辑 ①先输入一个字符串,然后judge1()函数遍历它,判断字符是否在[0,4]区间范围内 ②将输入的字符串用层次遍历的方式存储为一个二叉树root ③再将二叉树r…...

OsgEarth配置.earth文件支持wms服务
<!-- 参考 http://vmap0.tiles.osgeo.org/wms/vmap0?LAYERSbasic&SERVICEWMS&VERSION1.1.1&REQUESTGetMap&STYLES&FORMATimage%2Fjpeg&SRSEPSG%3A4326&BBOX-90,45,-45,90&WIDTH256&HEIGHT256 --> <!-- 可用 2023.03.09--> …...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...
