二叉树的顺序结构(堆的实现)
前言
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结 构存储。现实中我们通常把堆 ( 一种二叉树 ) 使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
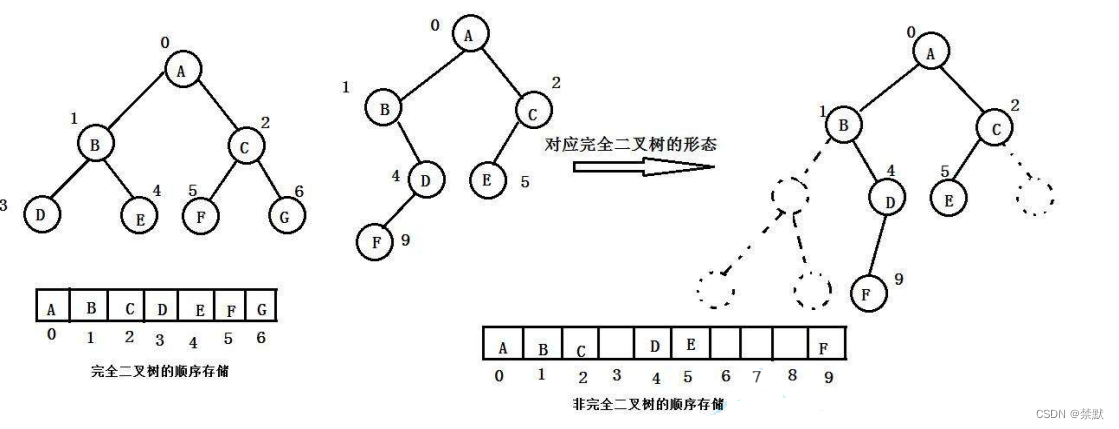
1.堆的概念及结构

2.堆的创建和功能实现
2.1堆的基本结构的创建和相关函数声明。
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>typedef int Datatype;
typedef struct Heap {Datatype* a;int size;int capacity;
}HP;
// 堆的初始化
void HeapInit(HP* hp);
// 堆的销毁
void HeapDestory(HP* hp);
// 堆的插入
void HeapPush(HP* hp, Datatype x);
// 堆的删除
void HeapPop(HP* hp);
// 取堆顶的数据
Datatype HeapTop(HP* hp);
// 堆的数据个数
bool HeapSize(HP* hp);
// 堆的判空
int HeapEmpty(HP* hp);
//向上调整
void Adjustup(Datatype* a, int child);
//向下调整
void Adjustdown(Datatype* a, int n, int parent);
//数据交换
void Swap(Datatype* p1, Datatype* p2);2.2 各函数的实现与讲解
2.1堆的初始化和销毁
堆的初始化和销毁与以前的动态数组实现顺序表和栈的初始化和销毁基本是一样的,在这里小编就不多解释了。
// 堆的初始化
void HeapInit(HP* hp) {assert(hp);hp->a = NULL;hp->size = hp->capacity = 0;
}
// 堆的销毁
void HeapDestory(HP* hp) {assert(hp);free(hp->a);hp->a = NULL;hp->size = hp->capacity = 0;
}2.2堆数据的插入
补充向上调整法
通过比较新插入元素与其父节点的值来判断是否需要进行交换。如果新插入元素的值大于父节点的值,就将它们进行交换,并更新索引值。这样,逐步向上调整,直到新插入元素找到了合适的位置,保证了堆的性质。
//向上调整
void Adjustup(Datatype* a,int child) {int parent = (child - 1) / 2;while (child > 0) {if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}这个是建立大堆的向上调整,建立小堆的话直接改成小于
每插入一个元素,调用一次向上调整函数。
// 堆的插入
void HeapPush(HP* hp, Datatype x) {assert(hp);if (hp->size == hp->capacity) {int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;Datatype* temp = (Datatype*)realloc(hp->a, sizeof(Datatype) * newcapacity);if (temp == NULL) {perror("realloc fail");return;}hp->a = temp;hp->capacity = newcapacity;}hp->a[hp->size] = x;hp->size++;Adjustup(hp->a, hp->size-1);
}例如数组a[]={1, 5, 3, 8, 7, 6},依次插入并建立大堆后的顺序是:
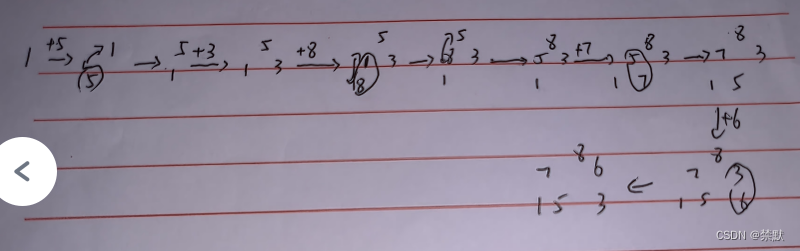
- 插入 1,堆变为 [1]
- 插入 5,堆变为 [5, 1]
- 插入 3,堆变为 [5, 1, 3]
- 插入 8,堆变为 [8, 5, 3, 1]
- 插入 7,堆变为 [8, 7, 3, 1, 5]
- 插入 6,堆变为 [8, 7, 6, 1, 5, 3]
所以,建立大堆后的顺序是 [8, 7, 6, 1, 5, 3]。
2.3堆的删除
补充向下调整法
在这里惯性思维是直接删除头顶数据,然后重新建堆,通过向上调整法,但是我们需要从最后一个元素依次遍历向上调整。
这里我们采用向下调整法。
删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组最后一个数据,再进行向下调整算法。
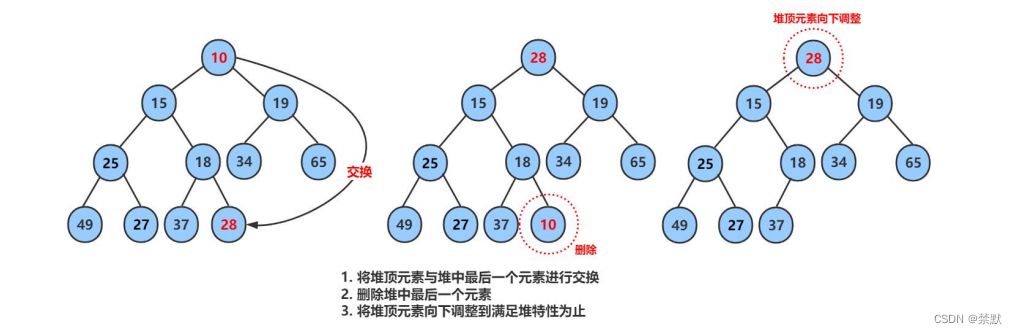
//向下调整
void Adjustdown(Datatype* a, int n, int parent) {//假设法,假设左孩子大int child = parent * 2 + 1;while (child < n ) {if (child + 1 < n && a[child + 1] > a[child])//a[child+1]<a[child]child = child + 1;if (a[child] > a[parent]) { //a[child]<a[parent]Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else break;}
}堆的删除
// 堆的删除
void HeapPop(HP* hp) {assert(hp);assert(hp->size > 0);Swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;Adjustdown(hp->a, hp->size, 0);
}最后我们会发现删除的数据是从大到小排列的,这里就可以牵扯到堆排序的应用,小编在下节会讲解的。
2.4其他函数实现(交换,判空,堆顶数据,数据个数)
//数据交换
void Swap(Datatype* p1, Datatype* p2) {Datatype temp = *p1;*p1 = *p2;*p2 = temp;
}
// 取堆顶的数据
Datatype HeapTop(HP* hp) {assert(hp);assert(hp->size > 0);return hp->a[0];
}
// 堆的数据个数
int HeapSize(HP* hp) {assert(hp);return hp->size;
}
// 堆的判空
bool HeapEmpty(HP* hp) {assert(hp);return hp->size == 0;}3.代码测试
#include "Heap.h"
void TestHeap1()
{int a[] = { 4,2,8,1,5,6,9,3,2,23,55,232,66,222,33,7,66,3333,999 };//int a[] = { 1,5,3,8,7,6 };HP hp;HeapInit(&hp);for (int i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);}printf("堆的大小为%d\n", HeapSize(&hp));int i = 0;while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));//a[i++] = HPTop(&hp);HeapPop(&hp);}printf("\n");
}
/*// 找出最大的前k个int k = 0;scanf("%d", &k);while (k--){printf("%d ", HeapTop(&hp));HeapPop(&hp);}printf("\n");HeapDestory(&hp);
}*/
int main(){
TestHeap1();
return 0;
}4.堆的选择题(方便大家理解)
1. 下列关键字序列为堆的是:(A)A 100 , 60 , 70 , 50 , 32 , 65 B 60 , 70 , 65 , 50 , 32 , 100 C 65 , 100 , 70 , 32 , 50 , 60D 70 , 65 , 100 , 32 , 50 , 60 E 32 , 50 , 100 , 70 , 65 , 60 F 50 , 100 , 70 , 65 , 60 , 322. 已知小根堆为 8 , 15 , 10 , 21 , 34 , 16 , 12 ,删除关键字 8 之后需重建堆,在此过程中,关键字之间的比较次数是(C)。A 1 B 2 C 3 D 43. 最小堆 [ 0 , 3 , 2 , 5 , 7 , 4 , 6 , 8 ], 在删除堆顶元素 0 之后,其结果是(C)A [ 3 , 2 , 5 , 7 , 4 , 6 , 8 ] B [ 2 , 3 , 5 , 7 , 4 , 6 , 8 ]C [ 2 , 3 , 4 , 5 , 7 , 8 , 6 ] D [ 2 , 3 , 4 , 5 , 6 , 7 , 8 ]
本节内容到此结束,下次小编将讲解堆排序的知识,欢迎大家捧场!!!
期待各位友友的三连和评论!!!
相关文章:

二叉树的顺序结构(堆的实现)
前言 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结 构存储。 现实中我们通常把堆 ( 一种二叉树 ) 使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事&…...

2024大模型如何学习【附学习资料】
摘要: 通过深入了解本文中的这些细节,并在实际项目中应用相关知识,将能够更好地理解和利用大模型的潜力,不仅在学术研究中,也在工程实践中。通过不断探索新方法、参与项目和保持热情,并将其应用于各种领域&…...
计算机组成原理·考点知识点整理
根据往年考试题,对考点和知识点的一个整理。 校验编码 码距 一种编码的最小码距,其实就是指这种编码的码距。码距有两种定义: 码距所描述的对象含义 2 2 2 个特定的码其二进制表示中不同位的个数一种编码这种编码中任意 2 2 2 个合法编码的…...

python-datetime模块时间戳常用方法汇总
文章目录 datetime模块常用方法1、导入模块2、获取当前日期和时间3、获取当前日期4、创建特定日期或时间5、日期和时间的运算6、使用timedelta运算日期时间创建 timedelta 对象timedelta 的加减运算timedelta 的属性timedelta 的比较示例代码格式化日期和时间获取日期和时间的各…...
【Python报错】已解决ModuleNotFoundError: No module named ‘timm’
成功解决“ModuleNotFoundError: No module named ‘timm’”错误的全面指南 一、引言 在Python编程中,经常会遇到各种导入模块的错误,其中“ModuleNotFoundError: No module named ‘timm’”就是一个典型的例子。这个错误意味着你的Python环境中没有安…...
⭐⭐⭐)
【设计模式】适配器模式(结构型)⭐⭐⭐
文章目录 1.概念1.1 什么是适配器模式1.2 优点与缺点 2.实现方式2.1 类适配器模式2.2 对象适配器模式 3 Java 哪些地方用到了适配器模式4 Spring 哪些地方用到了适配器模式 1.概念 1.1 什么是适配器模式 简单来说,适配器模式就是作为两个不兼容接口之间的桥梁。 1.…...

云原生周刊:Gateway API v1.1 发布 | 2024.6.3
开源项目推荐 Grafana Tanka Tanka 是 Grafana 开发的一款用于 Kubernetes 的灵活、可重用和简洁的配置工具,是使用 YAML 进行 Kubernetes 配置的一种替代方案。 pv-migrate pv-migrate 是一个 CLI 工具/kubectl 插件,可以轻松地将一个 Kubernetes PersistentVo…...

KotlinConf 2024:深入了解Kotlin Multiplatform (KMP)
KotlinConf 2024:深入了解Kotlin Multiplatform (KMP) 在近期的Google I/O大会上,我们推荐了Kotlin Multiplatform (KMP)用于跨移动、网页、服务器和桌面平台共享业务逻辑,并在Google Workspace中采用了KMP。紧接着,KotlinConf 2…...

探索ChatGPT-4在解决化学知识问题上的研究与应用
1. 概述 近年来,人工智能的发展主要集中在 GPT-4 等大型语言模型上。2023 年 3 月发布的这一先进模型展示了利用广泛知识应对从化学研究到日常问题解决等复杂挑战的能力。也开始进行研究,对化学的各个领域,从化学键到有机化学和物理化学&…...

性能狂飙:SpringBoot应用优化实战手册
在数字时代,速度就是生命,性能就是王道!《极速启航:SpringBoot性能优化的秘籍》带你深入SpringBoot的内核,探索如何打造一个飞速响应、高效稳定的应用。从基础的代码优化到高级的数据库连接池配置,再到前端…...
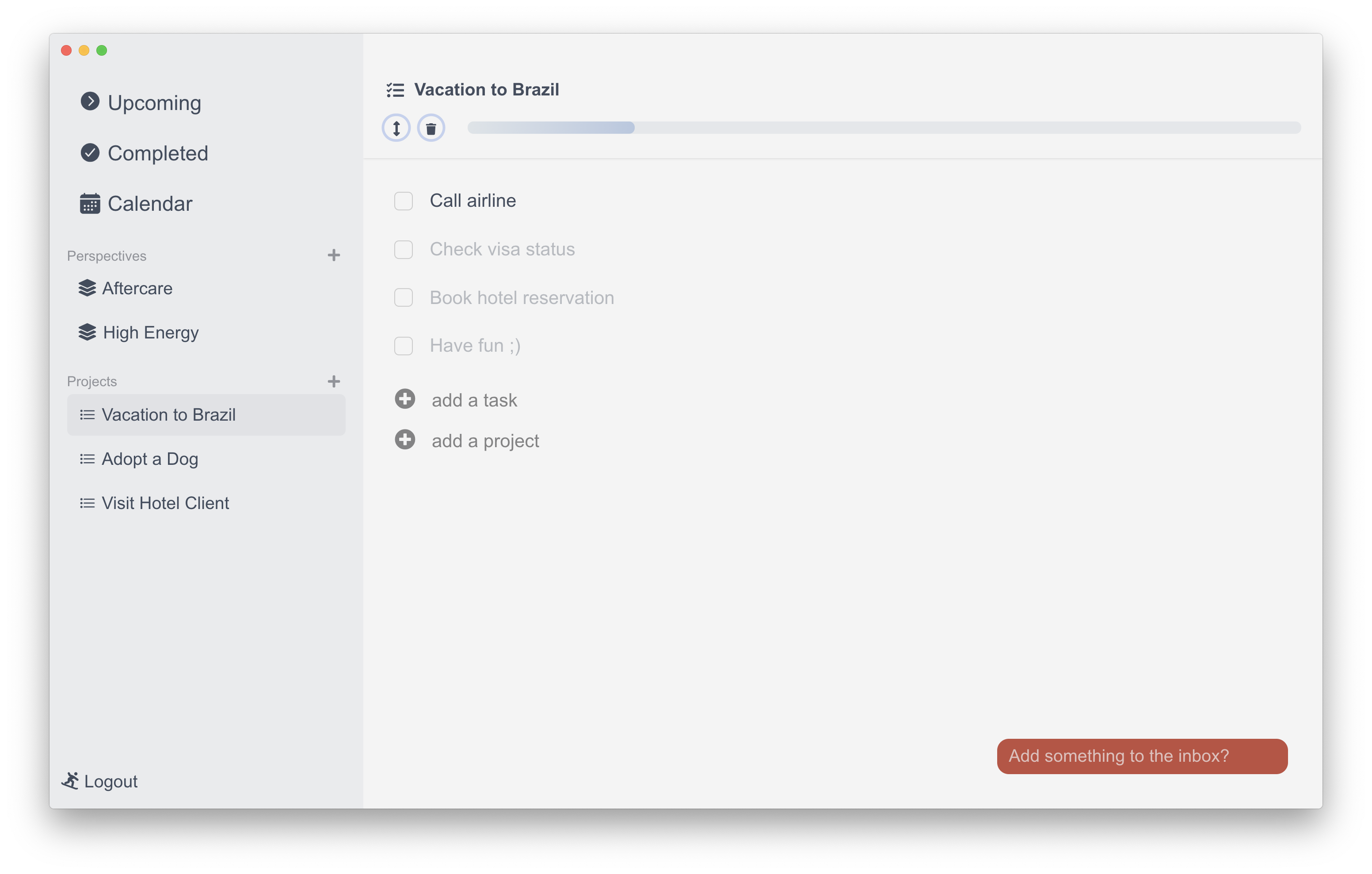
Github上一款开源、简洁、强大的任务管理工具:Condution
Condution 是一款开源任务管理工具,它以简洁易用、功能强大著称。它旨在为用户提供一个简单高效的平台,帮助他们管理日常任务、提高工作效率。 1. Condution 的诞生背景 现如今,市面上存在着许多任务管理软件,但它们往往价格昂贵…...

LeetCode-2938. 区分黑球与白球【贪心 双指针 字符串】
LeetCode-2938. 区分黑球与白球【贪心 双指针 字符串】 题目描述:解题思路一:贪心解题思路二:一次遍历统计1的个数,找0后累加左边的1的个数解题思路三: 题目描述: 桌子上有 n 个球,每个球的颜色…...

深度神经网络——什么是扩散模型?
1. 概述 在人工智能的浩瀚领域中,扩散模型正成为技术创新的先锋,它们彻底改变了我们处理复杂问题的方式,特别是在生成式人工智能方面。这些模型基于高斯过程、方差分析、微分方程和序列生成等坚实的数学理论构建。 业界巨头如Nvidia、Google…...

有代码冗余的检查工具嘛
是的,有一些代码质量工具可以帮助检查冗余代码。这些工具可以分析代码库,并识别出重复、冗余或不必要的代码片段。一些流行的代码质量工具包括: PMD: PMD 是一个开源的静态代码分析工具,支持多种编程语言,包括 Java、…...

3D培训大师:快速输出标准3D课件,打造沉浸式培训体验
随着技术的日新月异和市场的迅猛扩张,企业对员工专业技能培训的需求日益凸显。传统的培训方式往往依赖于实地操作、现场指导,这不仅需要大量的人力、物力和时间成本,而且存在安全风险。特别是化工、机械制造等行业,实操培训的成本…...
Python接口自动化测试:Json 数据处理实战
🍅 视频学习:文末有免费的配套视频可观看 🍅 点击文末小卡片 ,免费获取软件测试全套资料,资料在手,涨薪更快 上一篇说了关于json数据处理,是为了断言方便,这篇就带各位小伙伴实战一下…...
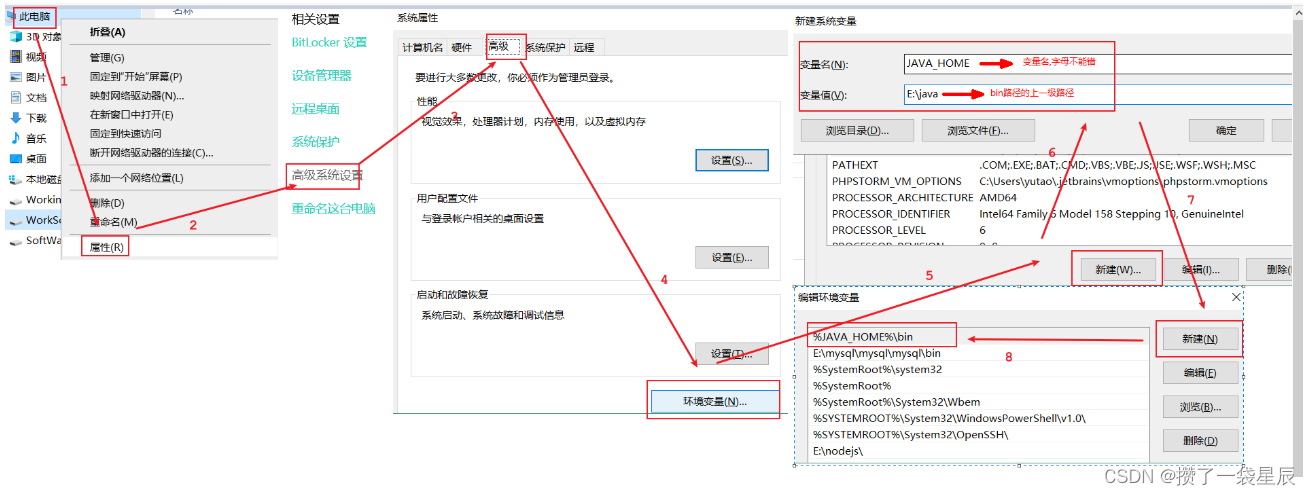
Java概述 , Java环境安装 , 第一个Hello World
环境变量,HelloWorld 1.会常用的dos命令 2.会安装java所需要的环境(jdk) 3.会配置java的环境变量 4.知道java开发三步骤 5.会java的入门程序(HelloWorld) 6.会三种注释方式 7.知道Java入门程序所需要注意的地方 8.知道println和print的区别第一章 Java概述 1.1 JavaSE体系介绍…...
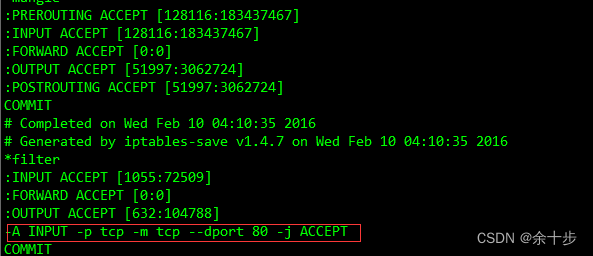
查看Linux端口占用和开启端口命令
查看端口的使用的情况 lsof 命令 比如查看80端口的使用的情况 lsof -i tcp:80列出所有的端口 netstat -ntlp查看端口的状态 /etc/init.d/iptables status开启端口以开启端口80为例。 1 用命令开启端口 iptables -I INPUT -p tcp --dport 80 -j accpet --写入要开放的端口/…...
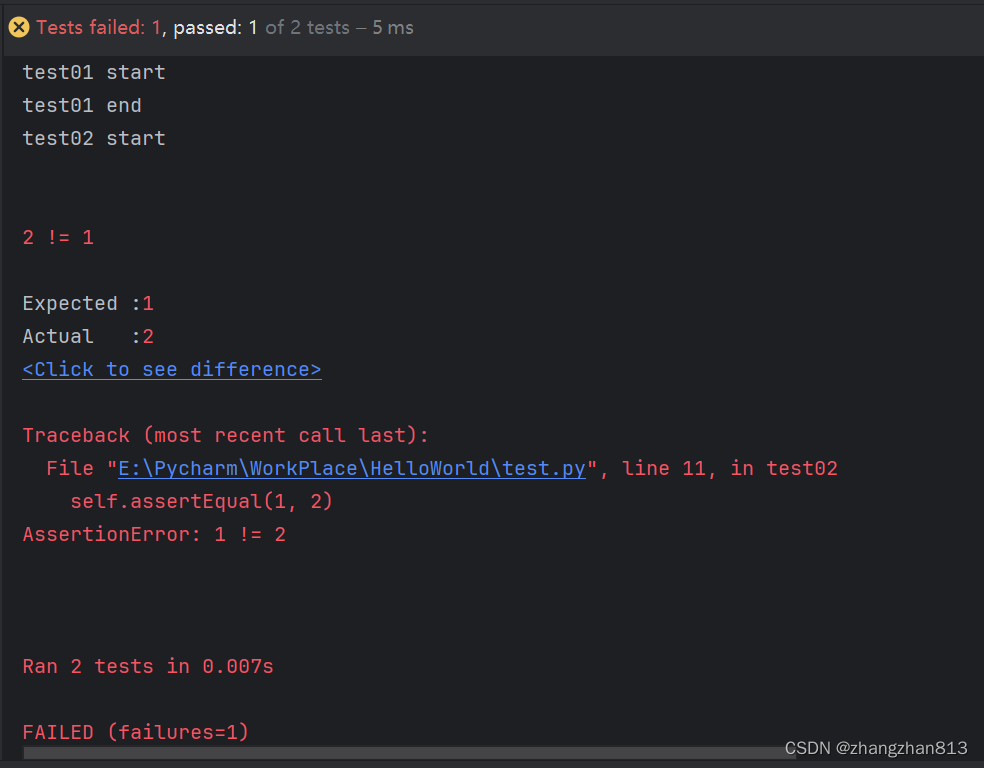
24-unittest简介
一、unittest简介 unittest是Python中常用的单元测试框架,与Java中的Junit单元测试框架类似。 二、示例程序 1)导入unittest模块 import unittest 2)使用help()函数查看源码中的示例程序 help(unittest) Simple usage:import unittestc…...
)
Kotlin 中,扩展函数(Extension Functions)
在 Kotlin 中,扩展函数(Extension Functions)是用于向已有的类添加新功能而无需继承或使用装饰模式的一个特性。这允许你通过更自然的语法为现有类型添加方法。 下面是一个简单的扩展函数示例: // 定义一个扩展函数,…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
