Python | C# | MATLAB 库卡机器人微分运动学 | 欧拉-拉格朗日动力学 | 混合动力控制
🎯要点
🎯正向运动学几何矩阵,Python虚拟机器人模拟动画二连杆平面机械臂 | 🎯 逆向运动学几何矩阵,Python虚拟机器人模拟动画三连杆平面机械臂 | 🎯微分运动学数学形态,Python模拟近似结果 | 🎯欧拉-拉格朗日动力学数学形态,Python模拟机器人操纵器推导的运动方程有效性 | 🎯运动规划算法,Python虚拟机器人和摄像头模拟离线运动规划算法 | 🎯移动导航卡尔曼滤波算法及其它方法,Python虚拟机器人模拟可检测和可磕碰 | 🎯混合动力控制微分数学形态,Python虚拟机器人模拟比例微分积分和逆动态控制 | 🎯阻抗控制,Python模拟二联(三联动)。
🎯 库卡机器人模拟 ,库卡实体机器人对象检测和颜色分割拾取和放置物体 | 🎯 C#远程测试虚拟机器人 | 🎯虚拟机器人从三维文件创建自定义模型。
🎯Cpp(Python)和MATLAB差动驱动ROS Raspberry Pi全功能机器人原型。
🍇Python逆动力学算法
逆动力学是指计算运动中的力。给定配置 q q q、广义速度 q ˙ \dot{ q } q˙ 和广义加速度 q ¨ \ddot{ q } q¨,相当于找到关节扭矩 τ \tau τ 和接触力 f ext f ^{\text {ext } } fext 使得运动约束方程得到满足:
M ( q ) q ¨ + q ˙ ⊤ C ( q ) q ˙ = S ⊤ τ + τ g ( q ) + τ est + J ( q ) ⊤ f ext J ( q ) q ¨ + q ˙ ⊤ H ( q ) q ˙ = 0 \begin{aligned} M ( q ) \ddot{ q }+\dot{ q }^{\top} C ( q ) \dot{ q } & = S ^{\top} \tau + \tau _g( q )+ \tau ^{\text {est }}+ J ( q )^{\top} f ^{\text {ext }} \\ J ( q ) \ddot{ q }+\dot{ q }^{\top} H ( q ) \dot{ q } & = 0 \end{aligned} M(q)q¨+q˙⊤C(q)q˙J(q)q¨+q˙⊤H(q)q˙=S⊤τ+τg(q)+τest +J(q)⊤fext =0
逆动力学的数学函数如下:
( τ , f e x t ) = ID ( q , q ˙ , q ¨ ) \left(\tau, f ^{e x t}\right)=\operatorname{ID}( q , \dot{ q }, \ddot{ q }) (τ,fext)=ID(q,q˙,q¨)
当我们的线性系统完全确定时,该函数定义明确,例如对于具有六个自由度的手臂,但对于在多个接触下的移动机器人,该函数通常是欠确定的。在这种情况下,我们可以将外力的计算转移到例如接触模型,并仅计算关节扭矩:
τ = RNEA ( q , q ˙ , q ¨ , f est ) \tau =\operatorname{RNEA}\left( q , \dot{ q }, \ddot{ q }, f ^{\text {est }}\right) τ=RNEA(q,q˙,q¨,fest )
递归牛顿-欧拉算法为我们提供了一种实现此功能的有效方法。该算法分为两步:前向传递,主要是二阶正向运动学,然后是后向传递,计算力和关节扭矩。
此算法第一遍计算主体速度 v i v _i vi 和加速度 a i a _i ai。从运动树的根 i = 0 i=0 i=0 开始,物体 i i i 的运动 v i , a i v _i, a _i vi,ai 是根据运动 v λ ( i ) , a λ ( i ) v _{\lambda(i)}, a _{\lambda( i)} vλ(i),aλ(i) 其父体 λ ( i ) \lambda(i) λ(i) 的分量,加上它们之间的关节的运动 q ˙ i , q ¨ i \dot{ q }_i, \ddot{ q }_i q˙i,q¨i 引起的分量。让我们从主体速度开始:
v i = i X λ ( i ) v λ ( i ) + S i q ˙ i v _i={ }^i X _{\lambda(i)} v _{\lambda(i)}+ S _i \dot{ q }_i vi=iXλ(i)vλ(i)+Siq˙i
在此方程中, i X λ ( i ) { }^i X _{\lambda(i)} iXλ(i) 是从 λ ( i ) \lambda(i) λ(i) 到 i i i 的 Plücker 变换, S i S _i Si 是关节的运动子空间矩阵。请注意, q ˙ i ∈ R k \dot{ q }_i \in R ^k q˙i∈Rk 是关节的速度,例如对于浮动底座(又名自由飞行器)关节, k = 6 k=6 k=6,对于球形关节, k = 2 k=2 k=2,对于旋转关节或棱柱关节, k = 1 k=1 k=1。无论如何, q ˙ i \dot{ q }_i q˙i 不是广义速度向量 q ˙ \dot{ q } q˙ 的 i th i^{\text {th }} ith 分量(这没有意义,因为 i i i 是关节的索引,而向量 q ˙ \dot{ q } q˙ 按自由度索引)。因此,运动子空间矩阵的维度为 6 × k 6 \times k 6×k。
接下来,让我们假设一个“常见”关节(旋转关节、棱柱关节、螺旋关节、圆柱关节、平面关节、球形关节、自由飞行关节),这样运动子空间矩阵的视在时间导数为零。除非你处理的是不同的关节,否则不要介意这句话。 然后,在前向传递过程中从父关节计算出的主体加速度为:
a i = i X λ ( i ) a λ ( i ) + S i q ¨ i + v i × S i q ˙ i a _i={ }^i X _{\lambda(i)} a _{\lambda(i)}+ S _i \ddot{ q }_i+ v _i \times S _i \dot{ q }_i ai=iXλ(i)aλ(i)+Siq¨i+vi×Siq˙i
到目前为止,该正向传递是二阶正向运动学。一路上我们要计算的最后一件事是由主体运动 v i v _i vi , a i a _i ai产生的主体惯性力:
f i = I i a i + v i × ∗ I i v i − f i est f _i= I _i a _i+ v _i \times{ }^* I _i v _i- f _i^{\text {est }} fi=Iiai+vi×∗Iivi−fiest
我们将在向后传递期间更新这些力向量。请注意,由于它们是力矢量,因此我们的符号意味着 f i ext f _i^{\text {ext }} fiext 也是一个物体力矢量。如果外力在惯性系中表示为 0 f i ext { }^0 f _i^{\text {ext }} 0fiext ,则可以通过以 f i = i X 0 0 f i e x t f _i={ }^i X _0{ }^0 f _i^{e x t} fi=iX00fiext 映射到主体框架 。
此算法的第二遍计算体积力。从运动树的叶节点开始,物体 i i i 的广义力 f i f _i fi 被添加到迄今为止为其父代 λ ( i ) \lambda(i) λ(i) 计算的力 f λ ( i ) f _{\lambda(i)} fλ(i) :
f λ ( i ) = f λ ( i ) + i X λ ( i ) ⊤ f i f _{\lambda(i)}= f _{\lambda(i)}+{ }^i X _{\lambda(i)}^{\top} f _i fλ(i)=fλ(i)+iXλ(i)⊤fi
一旦计算出主体 i i i 上的广义力 f i f _i fi,我们就可以通过沿关节轴投影该 6D 主体矢量来获得相应的关节扭矩 τ i \tau _i τi:
τ i = S i ⊤ f i \tau _i= S _i^{\top} f _i τi=Si⊤fi
对于旋转关节, S i S _i Si 是一个 6 × 1 6 \times 1 6×1 列向量,因此我们以单个数字 τ i = S i ⊤ f i \tau_i= S _i^{\top} f _i τi=Si⊤fi 结尾:关节伺服系统应提供的驱动扭矩提供跟踪 ( q , q ˙ , q ¨ , f e x t ) \left( q , \dot{ q }, \ddot{ q }, f ^{e x t}\right) (q,q˙,q¨,fext)。所有其他组件对应于我们的旋转关节的五度约束,并将由关节的力学被动提供。
现在让我们通过在伪 Python 中执行相同的操作来明确更多的事情。我们的(此算法)函数原型是:
def rnea(q, qd, qdd, f_ext):pass
请注意,q 是每个关节的广义坐标列表,而不是平面数组,其他参数也是如此。特别是,f_ext 是体力矢量 f i ext f _i^{\text {ext }} fiext 的列表。使用 Python 类型注释,我们的原型将如下所示:
from typing import Listimport numpy as npdef rnea(q: List[np.ndarray],qd: List[np.ndarray],qdd: List[np.ndarray],f_ext: List[np.ndarray],
) -> List[np.ndarray]:pass
这种额外的结构允许更通用的关节,例如球形关节(不常见)或用于移动机器人浮动底座的自由飞行关节(常见)。如果所有关节都是旋转的,那么所有类型都将合并为平面阵列。
让我们用 v 0 = 0 v _0= 0 v0=0 表示运动树根链接的空间速度,用 a 0 a _0 a0 表示其空间加速度。我们将它们分别初始化为零和标准重力加速度:
n = len(qd) - 1 # number of links == number of joints - 1
v = [np.empty((6,)) for i in range(n + 1)]
a = [np.empty((6,)) for i in range(n + 1)]
f = [np.empty((6,)) for i in range(n + 1)]
tau = [np.empty(qd[i].shape) for i in range(n + 1)]
v[0] = np.zeros((6,))
a[0] = -np.array([0.0, 0.0, -9.81])
我们继续前向传递,范围从链接 i = 1 i=1 i=1 到树的最后一个链接 i = n i=n i=n:
for i in range(1, n + 1):p = lambda_[i] # p for "parent"X_p_to_i[i], S[i], I[i] = compute_joint(joint_type[i], q[i])v[i] = X_p_to_i[i] * v[p] + S[i] * qd[i]a[i] = X_p_to_i[i] * a[p] + S[i] * qdd[i] + spatial_cross(v[i], S[i] * qd[i])f[i] = I[i] * a[i] + spatial_cross_dual(v[i], I[i] * v[i]) - f_ext[i]
向后传递以相反的顺序遍历相同的范围:
for i in range(n, 0, -1):p = lambda_[i]tau[i] = S[i].T * f[i]f[p] += X_p_to_i[i].T * f[i]
最终,我们得到:
def rnea(q, qd, qdd, f_ext):n = len(qd)v = [np.empty((6,)) for i in range(n + 1)]a = [np.empty((6,)) for i in range(n + 1)]f = [np.empty((6,)) for i in range(n + 1)]tau = [np.empty(qd[i].shape) for i in range(n + 1)]v[0] = np.zeros((6,))a[0] = -np.array([0.0, 0.0, -9.81])for i in range(1, n + 1):p = lambda_[i]X_p_to_i[i], S[i], I[i] = compute_joint(joint_type[i], q[i])v[i] = X_p_to_i[i] * v[p] + S[i] * qd[i]a[i] = X_p_to_i[i] * a[p] + S[i] * qdd[i] + spatial_cross(v[i], S[i] * qd[i])f[i] = I[i] * a[i] + spatial_cross_dual(v[i], I[i] * v[i]) - f_ext[i]for i in range(n, 0, -1):p = lambda_[i]tau[i] = S[i].T * f[i]f[p] += X_p_to_i[i].T * f[i]return tau
长度不同的数组列表通常是刚体动力学库或模拟器中的内部结构。从此类列表到平面数组结构的映射称为关节,并决定如何表示球形和自由飞行关节的方向。
👉参阅:亚图跨际
相关文章:

Python | C# | MATLAB 库卡机器人微分运动学 | 欧拉-拉格朗日动力学 | 混合动力控制
🎯要点 🎯正向运动学几何矩阵,Python虚拟机器人模拟动画二连杆平面机械臂 | 🎯 逆向运动学几何矩阵,Python虚拟机器人模拟动画三连杆平面机械臂 | 🎯微分运动学数学形态,Python模拟近似结果 | …...
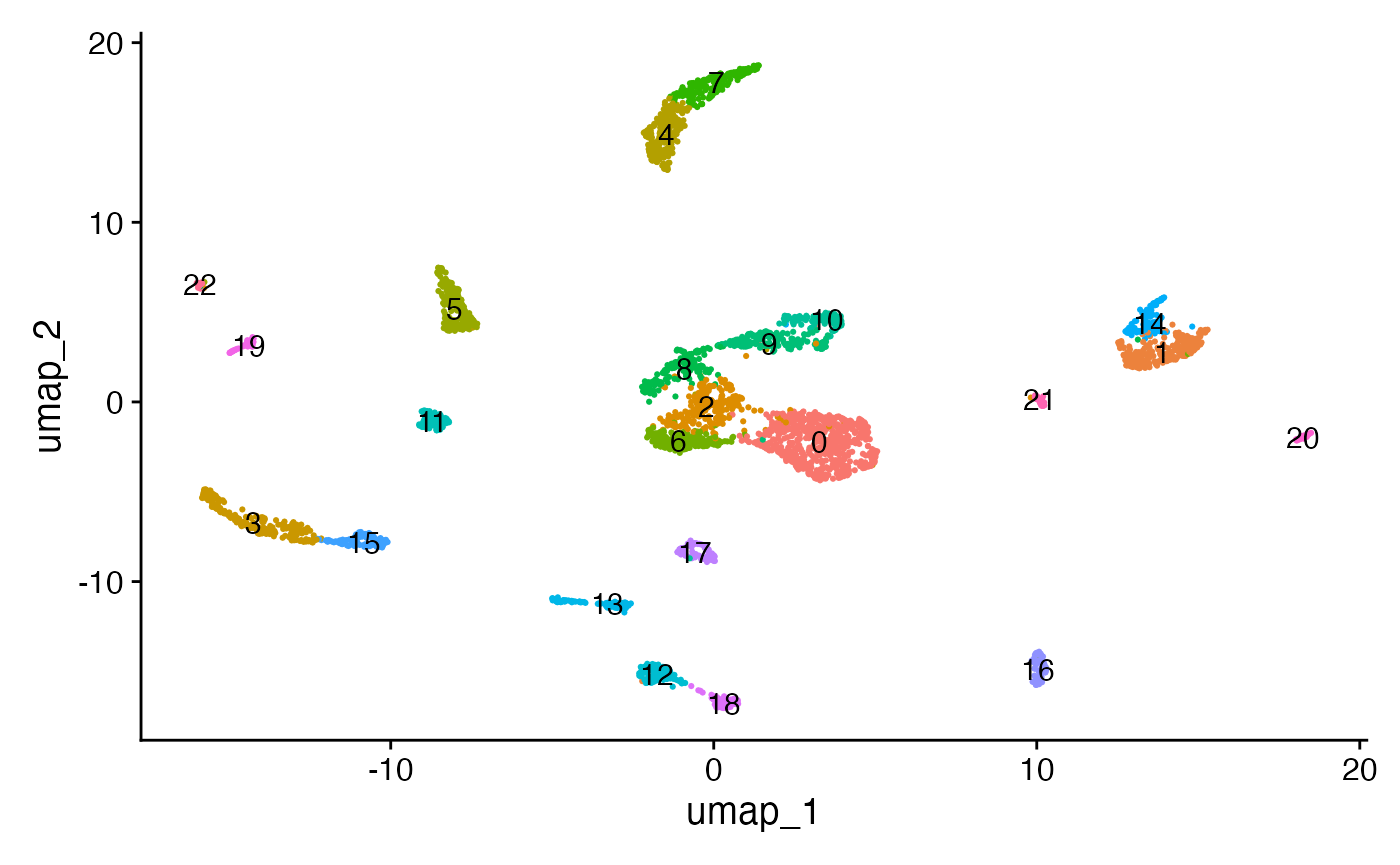
Signac|成年小鼠大脑 单细胞ATAC分析(1)
引言 在本教程中,我们将探讨由10x Genomics公司提供的成年小鼠大脑细胞的单细胞ATAC-seq数据集。本教程中使用的所有相关文件均可在10x Genomics官方网站上获取。 本教程复现了之前在人类外周血单核细胞(PBMC)的Signac入门教程中执行的命令。…...

【POSIX】运行时so库动态加载
运行时可以自己自定义so库的动态加载框架,主动去加载某些库,并调用其中的某些方法 首先写一些方法,并生成so库 // hello.cpp#include <iostream>/*使用 nm 命令查看 so 库的内容 */// 1. 使用extern // dlsym(handle, "hello&qu…...
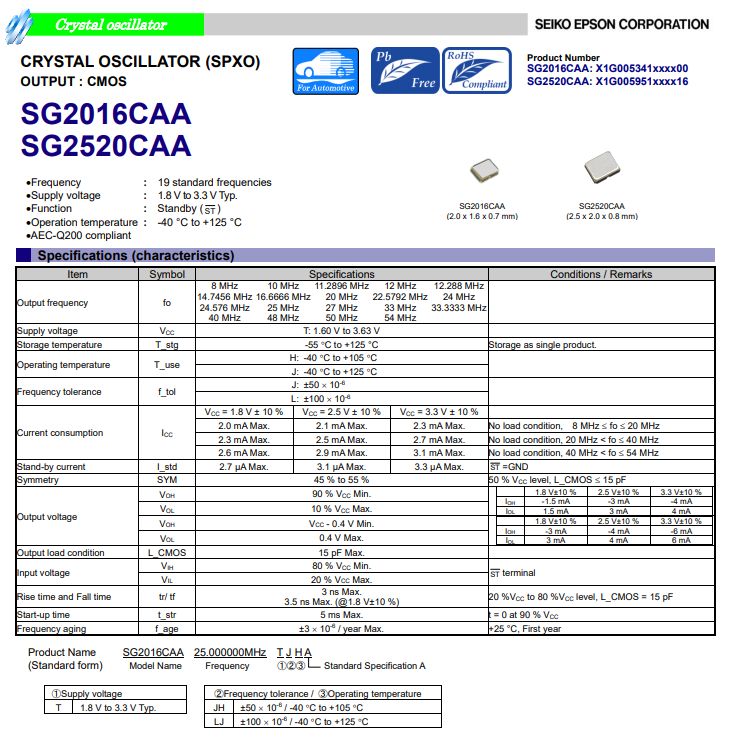
爱普生SG2520CAA汽车电子中控专用晶振
随着汽车电子技术的飞速发展,汽车中控系统变得越来越智能化和复杂化。为了确保这些系统的高性能和高可靠性,选择符合AEC-Q200标准的高品质晶振至关重要。爱普生SG2520CAA晶振凭借其优异的特性,成为汽车电子中控系统的理想选择。 爱普生晶振SG…...
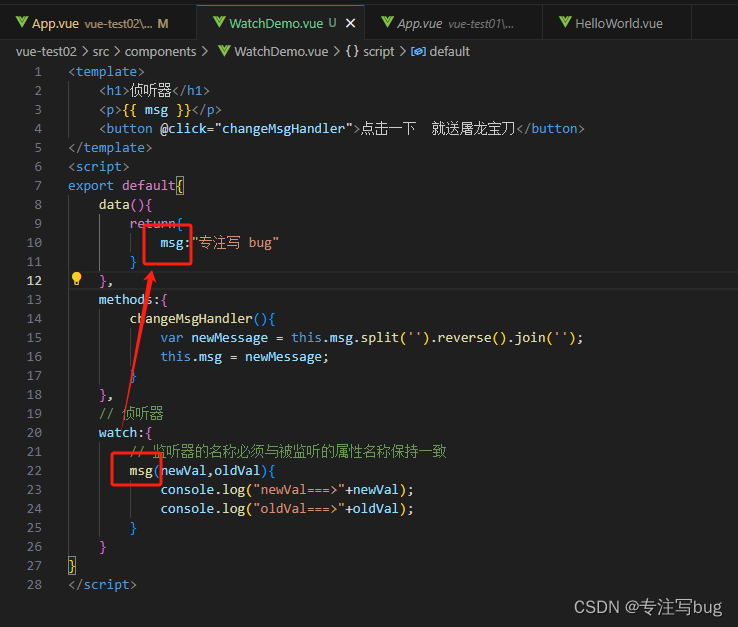
Vue——监听器简单使用与注意事项
文章目录 前言编写简单demo注意事项 前言 监听器,在官网中称为侦听器,个人还是喜欢称之为监听器。官方文档如下: vue 官网 侦听器 编写简单demo 侦听器在项目中通常用于监听某个属性变量值的变化,并根据该变化做出一些处理操作。…...

OpenCV的“画笔”功能
类似于画图软件的自由笔刷功能,当按住鼠标左键,在屏幕上画出连续的线条。 定义函数: import cv2 import numpy as np# 初始化参数 drawing False # 鼠标左键按下时为True ix, iy -1, -1 # 鼠标初始位置# 鼠标回调函数 def mouse_paint(…...
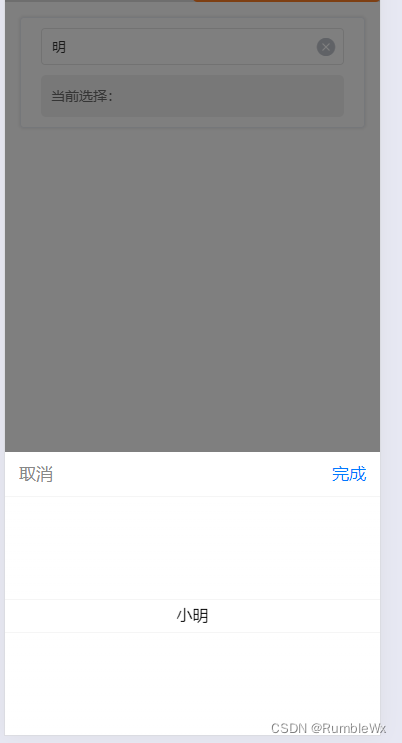
uniapp封装picker选择器组件,支持关键字查询
CommonPicker.vue组件 路径在 components\CommonPicker.vue <template><view><uni-easyinput v-model"searchQuery" :placeholder"placeholder" /><picker :range"filteredOptions" :range-key"text" v-model&…...
智慧城市的规划与实施:科技引领城市运行效率新飞跃
随着信息技术的飞速发展,智慧城市的构想正逐步成为现实。作为地理信息与遥感领域的研究者,我深知在这一转型过程中,技术的创新与应用是提升城市运行效率的关键。本文旨在探讨如何利用地理信息系统(GIS)、遥感技术、大数…...
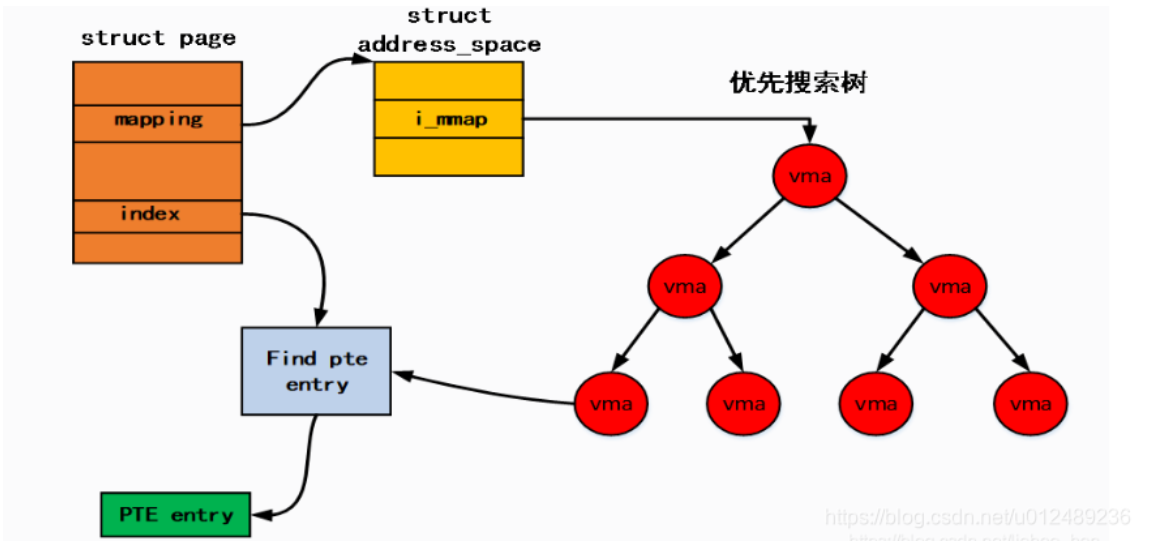
Linux——内存管理代码分析
虚空间管理 页框和页的关系 页框 将内存空间分为一个个大小相等的分区(比如:每个分区4KB),每个分区就是一个页框,也叫页帧,即物理页面,是linux划分内存空间的结果。 每个页框都有一个页框号,即内存块号、物理块号。 页 将用户…...
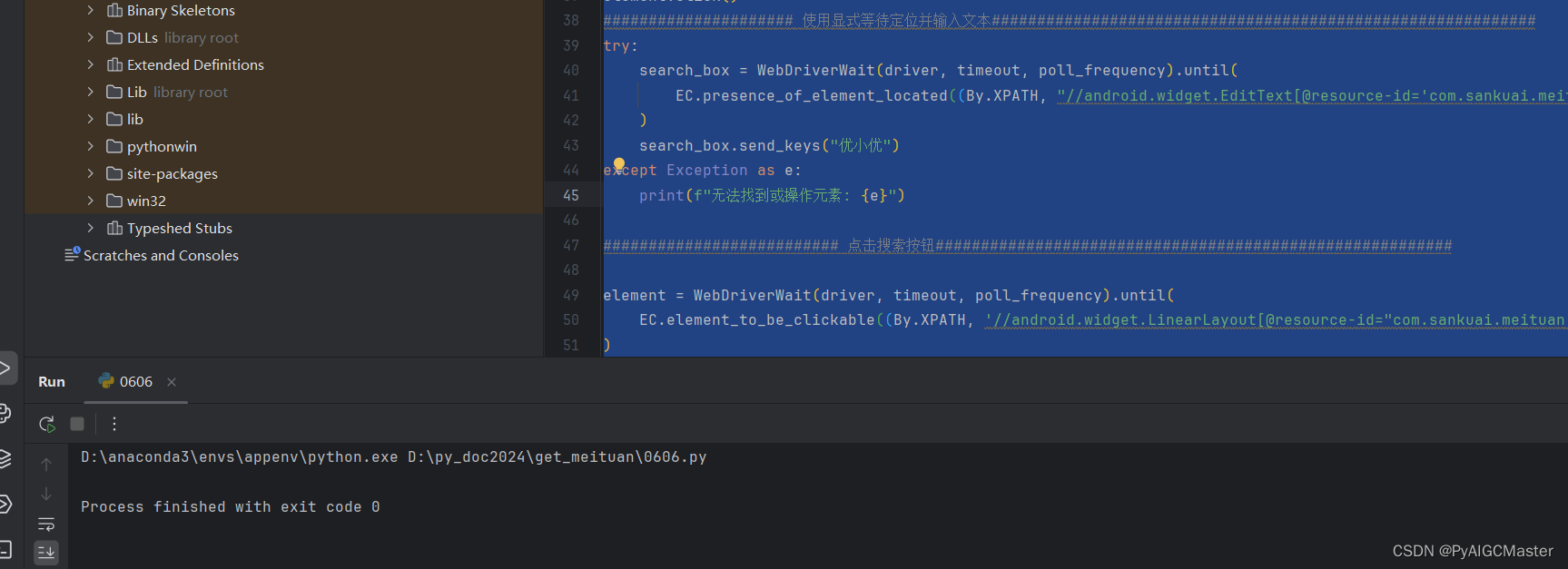
手机自动化测试:4.通过appium inspector 获取相关app的信息,以某团为例,点击,搜索,获取数据等。
0.使用inspector时,一定要把不相关的如weditor啥的退出去,否则,净是事。 1.从0开始的数据获取 第一个位置,有时0.0.0.0,不可以的话,你就用这个。 第二个位置,抄上。 直接点击第三个启动。不要…...
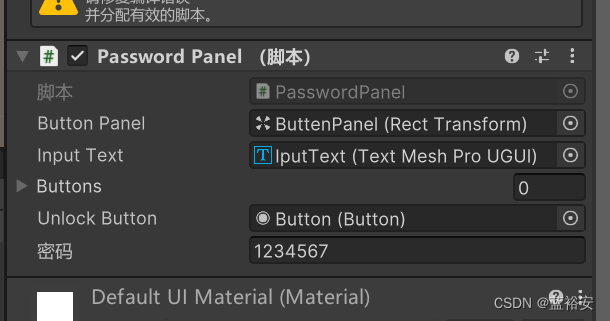
个人项目———密码锁的实现
布局组件 布局效果 组件绑定 密码锁的实现代码 using TMPro; using UnityEngine; using UnityEngine.UI;public class PasswordPanel : MonoBehaviour {// public Button button;// 所有按键的父物体public Transform buttonPanel;// 输入字符串的文本框public TMP_Text input…...

关于Input【type=number】可以输入e问题及解决方案
一、为什么 因为在数学里e 代表无理数,e是自然对数的底数,同时它又是一个无限不循环小数,所以我们在输入 e 时,输入框会默认 e 是数字,从而没有对它进行限制。 二、解决方案 小提示:vue下监听事件需要加n…...
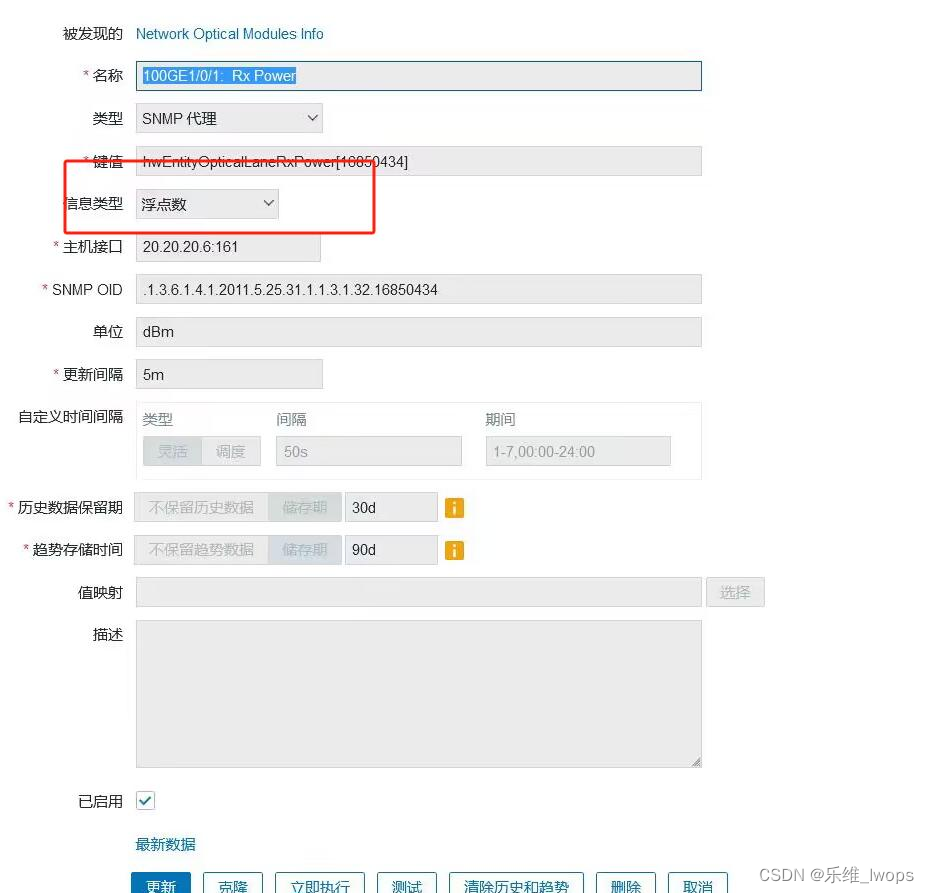
zabbix“专家坐诊”第241期问答
问题一 Q:华为交换机的100GE 1/0/1口的光模块收光值监测不到,有没有人碰到过这个问题呢?其他的端口都能监测到收光值,但是100GE 1/0/1口监测不到收光值。底层能查到,zabbix 6.0监控不到,以下是端口的报错信…...
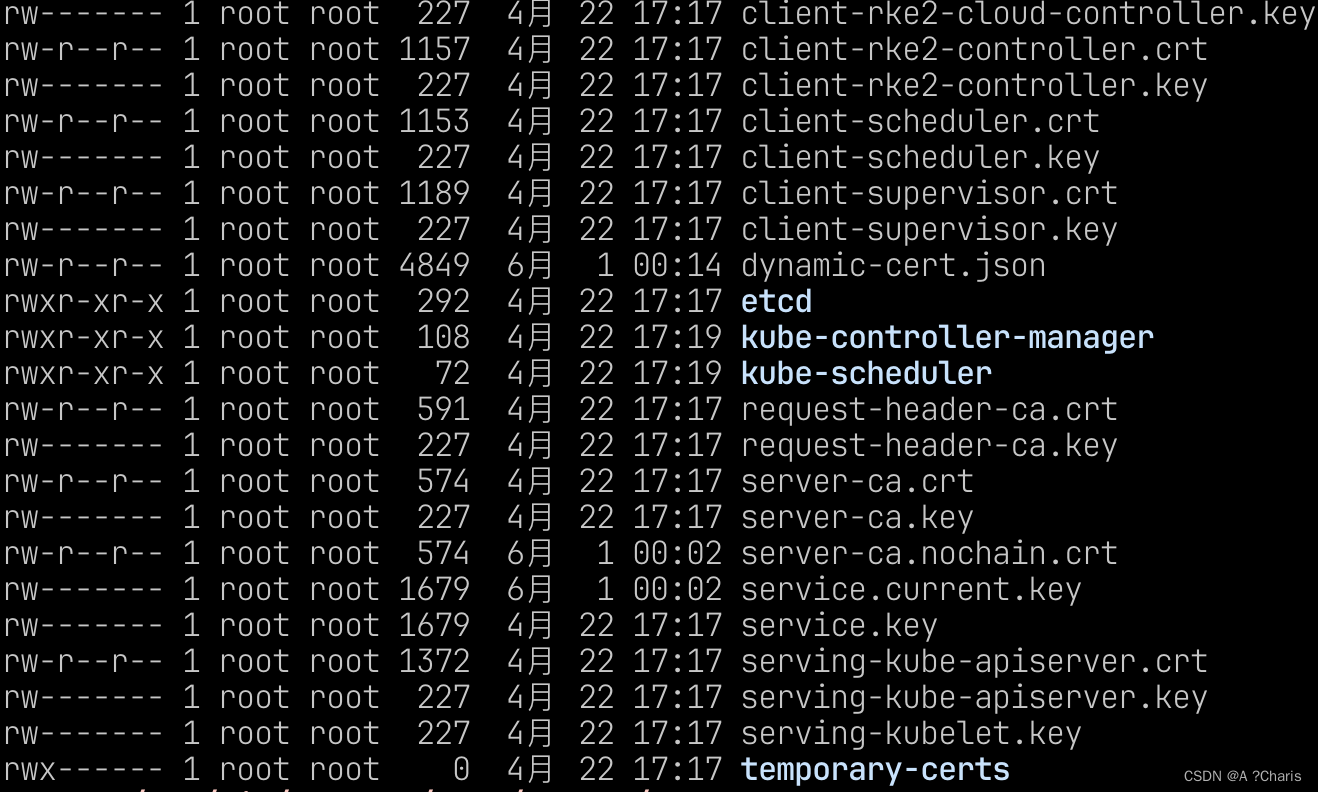
了解Kubernetes-RKE2的PKI以及证书存放位置
一、什么是PKI? 简称:证书基础设施。 可以方便理解为当你的集群有Server,Client架构,那么为了安全加密之间的通信,则需要使用证书进行交互,那么利用PKI架构可以安全加密组件之间的通信。 二、Kubernetes的PKI架构什…...

利用大语言模型进行事实匹配
论文地址:Automated Claim Matching with Large Language Models: Empowering Fact-Checkers in the Fight Against Misinformation | Companion Proceedings of the ACM on Web Conference 2024 WWW 2024 Automated Claim Matching with Large Language Models: Empowering F…...

【Stable Diffusion】(基础篇一)—— Stable Diffusion的安装
本系列笔记主要参考B站nenly同学的视频教程,传送门:B站第一套系统的AI绘画课!零基础学会Stable Diffusion,这绝对是你看过的最容易上手的AI绘画教程 | SD WebUI 保姆级攻略_哔哩哔哩_bilibili **Stable Diffusion(简称…...

维纳运动的概念
维纳运动(Wiener Process),也称为标准布朗运动,是一种重要的随机过程,广泛应用于数学、物理学和金融学等领域。它是一个连续时间的随机过程,具有一些特殊的性质,使其成为描述随机动态系统的经典…...
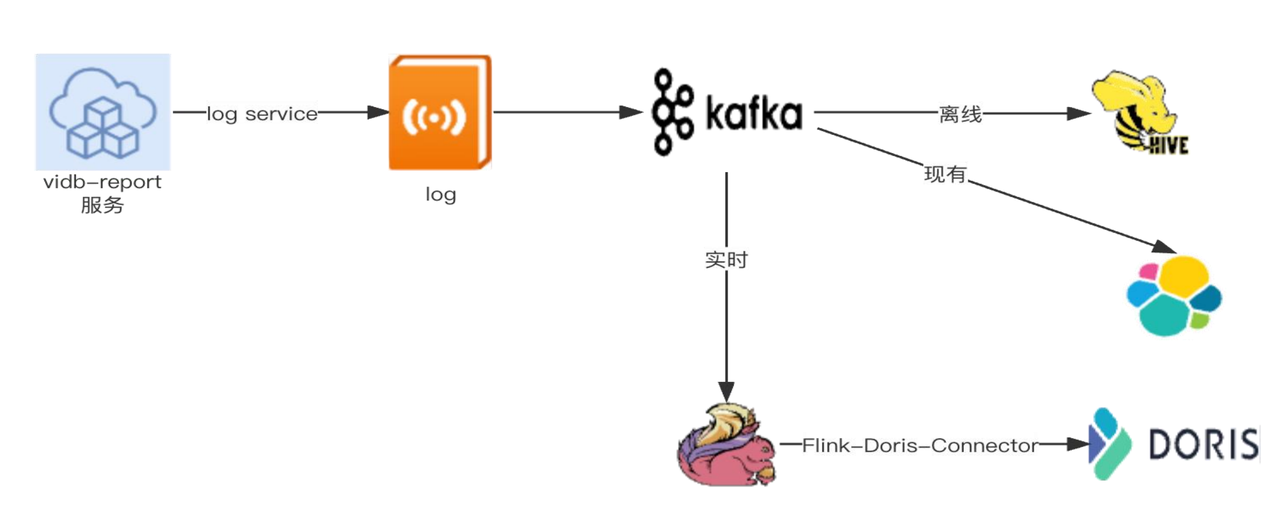
毫秒级查询性能优化实践!Apache Doris 在极越汽车数字化运营和营销方向的解决方案
作者:韩同阳,极越汽车大数据架构师,Apache Doris Active Contributor 编辑整理:SelectDB 技术团队 导读:极越是高端智能汽车机器人品牌,基于领先的百度 AI 能力和吉利 SEA 浩瀚架构生态赋能,致…...

vllm 大模型量化微调推理使用: lora、gptq、awq
1)微调lora模型推理 docker run --gpus all -v /ai/Qwen1.5-7B-Chat:/qwen-7b -v /ai/lora:/lora -p 10860:10860 --...
 自动测评方法)
WPS/Office(Word、Excel、PPT) 自动测评方法
在各高等、中等院校的计算机类课程中,计算机基本应用技能的上机操作考试,广受重视,大为盛行。其中,office(word、excel、ppt)上机考试最为普遍。于是,实现这类Office文档操作的自动阅卷评分,很有必要。本人最近项目上刚好遇到需要解决这种自动评分的问题,所以再次记录下解决的…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...

Excel 怎么让透视表以正常Excel表格形式显示
目录 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总...
