激活函数对比

激活函数

        sigmoid / tanh / relu / leaky relu / elu / gelu / swish

1、sigmoid  

优缺点

        1) 均值!=0，导致f=wx+b求导时，方向要么全正要么全负

                可以通过batch批量训练来缓解

        2) 输入值大于一定范围梯度就会消失

        3) 运算复杂

• 

2、tanh

优缺点

1) 均值=0

2) 计算复杂

3) 梯度消失

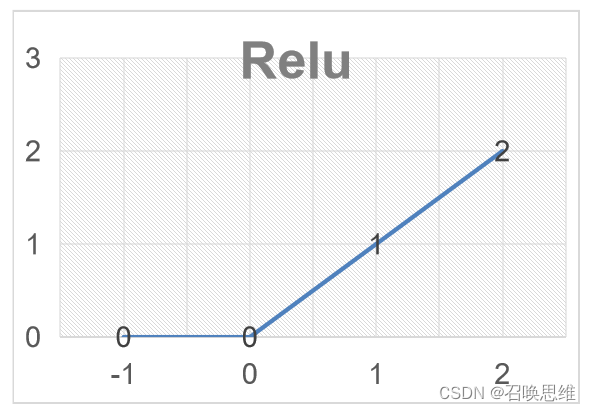
3、Relu (0,x)

优点

        1) 没有梯度消失问题

        2) 计算速度快

        3) 收敛速度比sigmoid/tanh快很多

缺点

        1) 也非0均值

        2) dead unit，权重初始化不好，导致多数样本在某个单元上<0，则永远失效

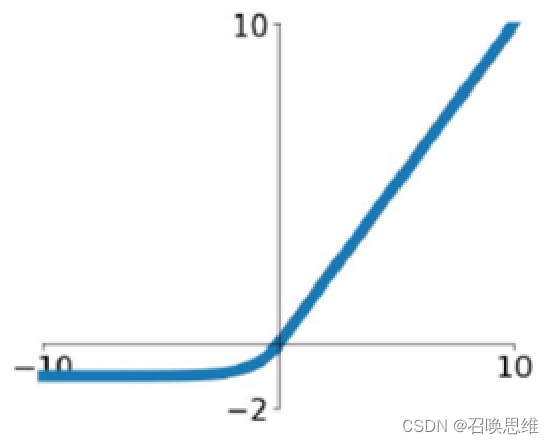
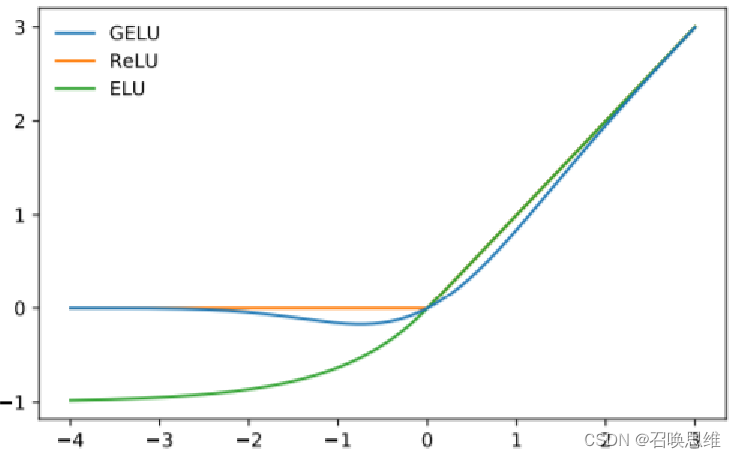
4、ELU

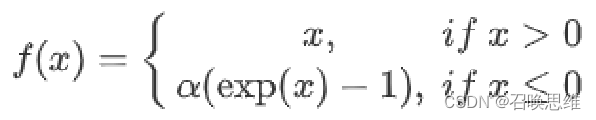
优缺点

1）均值接近0，最小值-1

2）没有dead unit

3）计算量变大

4）实验效果比relu稍好

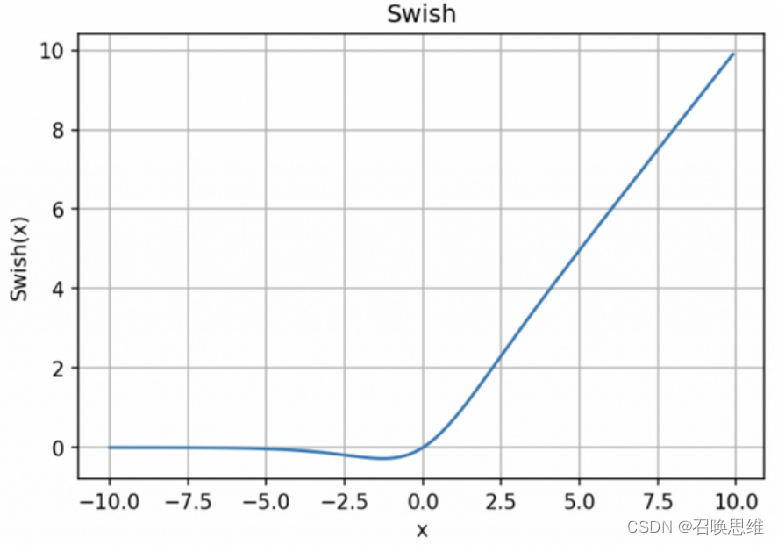
5、swish

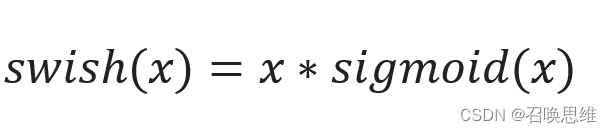
优缺点

        1）导数平滑，没有不可导点

        2）导数总是有值，没有dead unit

6、gelu

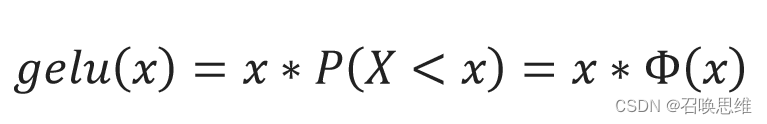
Φ(x)=高斯分布的累积分布与sigmoid图形近似

gelu(x)≈x∗σ(1.7x)

优缺点与swish类似