实验三-8086指令的应用《计算机组成原理》
一、实验目的
掌握8086指令的应用
二、实验原理
三、实验仪器
计算机1台,emu8086软件。
四、实验步骤
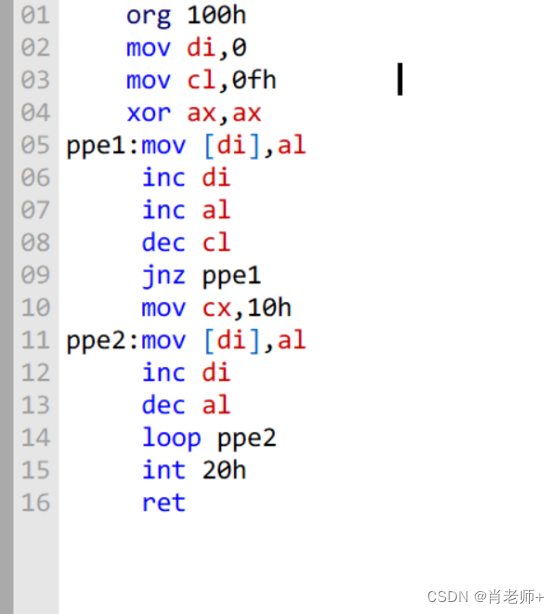
1、建立00H~0FH~00H 31个数,00H~0FH数据逐渐增大,0FH~00H逐渐减小,即DI指针所表示的地址中依次填入00H~0FH~00H 31个数,编写程序完成
步骤如下:
(1)如图,输入如下指令:
(2)点击“模拟”按钮后内存中的结果。
(3)点击“单步运行”,观察程序执行过程中的各个结果。特别是寄存器中值的变化,执行程序前后它们的值的变化(颜色的变化就是值的变化)。
(4)最后程序结果。寄存器中值的变化。
内存中值的情况:
(2)点击“模拟”按钮后内存中的结果。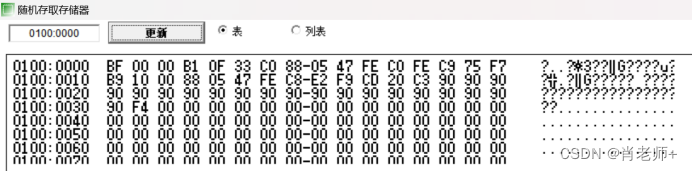
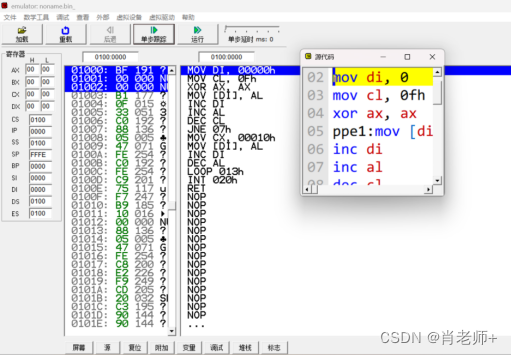
(3)点击“单步运行”,观察程序执行过程中的各个结果。特别是寄存器中值的变化,执行程序前后它们的值的变化(颜色的变化就是值的变化)。
变化前: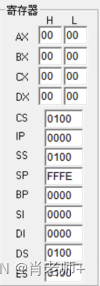
变化后: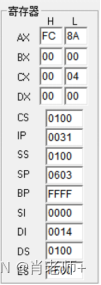
(4)最后程序结果。寄存器中值的变化。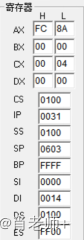
内存中值的情况:

实验反思:程序中的CX的值,在程序中的作用是什么?CLD和STD指令的作用?
"CX"通常在汇编语言(x86体系)中是一个16位或32位的寄存器,用于存放循环计数器。在循环结构如rep指令中,CX被用来跟踪重复操作的次数。它的作用是在循环内执行特定指令的次数,直到CX值减为零。
"CX"的值在循环控制、内存访问等场合非常重要,因为它直接影响到代码的执行流程。
“C”(即Character,字符)在某些编程上下文中可能表示字符类型的变量,但这个上下文与汇编中的CX有所不同,它指的是单个的字符数据而不是循环变量。
“CLD”(Clear Direction Flag)和"STD"(Set Direction Flag)是Intel x86指令集中的两条控制指令。CLD指令用于清除方向标志(DF),这是一个标志位,通常在处理字符串操作时使用,以决定字节数据是按从低地址到高地址(正向)还是高地址到低地址(反向)读取。当DF被清除时,默认为正向。而STD指令则是设置方向标志,恢复DF为正向。
相关文章:

实验三-8086指令的应用《计算机组成原理》
一、实验目的 掌握8086指令的应用 二、实验原理 三、实验仪器 计算机1台,emu8086软件。 四、实验步骤 1、建立00H~0FH~00H 31个数,00H~0FH数据逐渐增大,0FH~00H逐渐减小,即DI指针所表示的地…...
《维汉翻译通》App全新升级:维吾尔语短文本翻译、汉语拼音标注、维语词典、谚语格言名句等功能统统免费!还支持维吾尔文OCR识别提取文字!
2024年《维汉翻译通》App迎来重大更新!这次升级不仅带来了全新的功能,还为所有用户提供了更加便捷的服务体验。以下是我们新版本的主要亮点: 维语短文本翻译免费啦! 我们深知语言是沟通的桥梁,为了让更多人能够跨越语…...

全年申报!2024年陕西省双软企业认定条件标准、申报好处费用
1.双软企业是什么? 答:双软认证并不是一个资质,而是"软件产品登记"和"软件企业认定"两个不同资质的统称.叫做"双软企业" 2.双软企业的优惠政策是什么? 答:(1)软件产品登记的优惠政策:软件产品增值税,从13%减按3%征收,实行即征即退; (2)软件…...
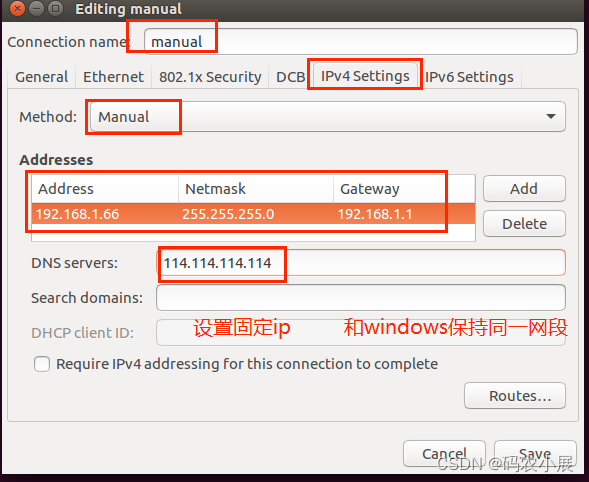
系统移植 (以将Linux系统移植到S5P6818开发板为例)
(本篇文章以将Linux系统移植到S5P6818开发板为例) 本文章所需要的文件在下面链接获取:https://download.csdn.net/download/a1547998353/89406544 开发环境搭建 1、安装交叉编译工具链 安装步骤: 1. 在ubuntu的家目录(~)下,创建t…...

超长正整数的加法
一、引言 在计算机科学中,整数加法是一个基础且重要的操作。然而,当面对超长正整数(即超出计算机内置整数类型表示范围的整数)时,传统的整数加法方法便不再适用。超长正整数通常使用字符串或数组来表示,每…...
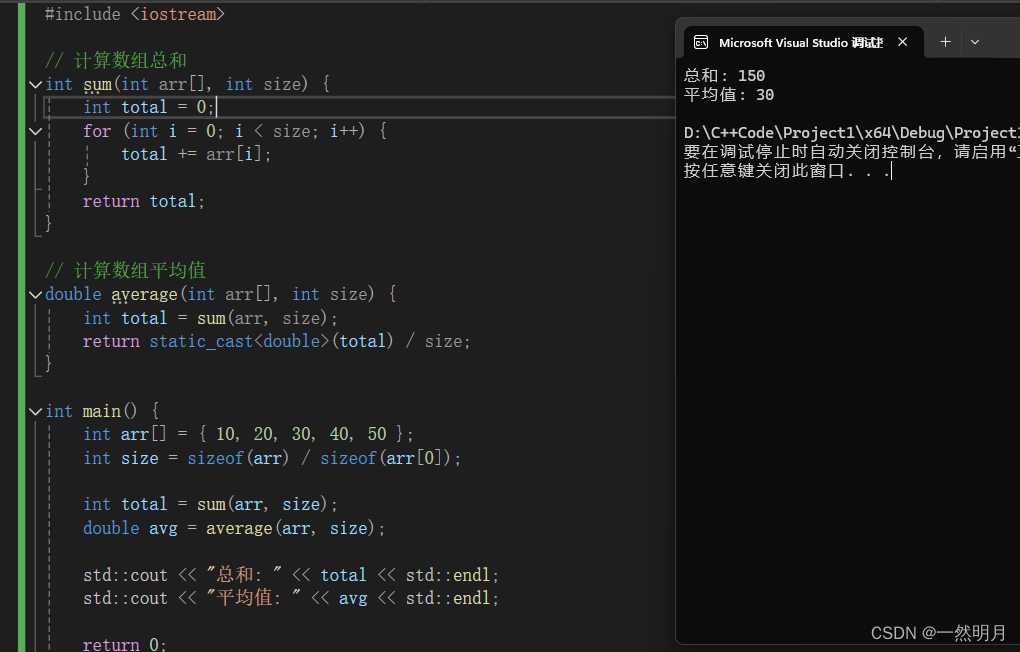
C++ - 查找算法 和 其他 算法
目录 一. 查找算法: 1.顺序查找: 2.二分查找: 二. 其他算法: 1.遍历算法: 2.求和、求平均值等聚合算法。 a.求和算法: b.求平均值算法: 一. 查找算法: 1.顺序查找࿱…...
和槽(SLOT)的宏连接方式弊端)
字符串的信号(SIGNAL)和槽(SLOT)的宏连接方式弊端
字符串的信号(SIGNAL)和槽(SLOT)的宏连接方式在 Qt 4 及早期版本中广泛使用,但这种方法确实存在一些缺点,主要包括以下几点: 类型安全性缺失:由于 SIGNAL 和 SLOT 宏接受的是字符串参…...

Kali linux学习入门
Kali linux学习入门 文章目录 Kali linux学习入门Kali Linux简介Kali Linux工具篇Kali Docker安装Docker 更换国内镜像源Kali 安装 docker compose Kali Linux文档篇Kali Linux 社区篇 Kali Linux简介 Kali Linux是专门用于渗透测试linux操作系统,它由BackTrack发展…...

selenium中,怎么判断是否已选多选框
html文件 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title> </head> <body><p>测试勾选</p><div><input type"checkbox" name"b…...
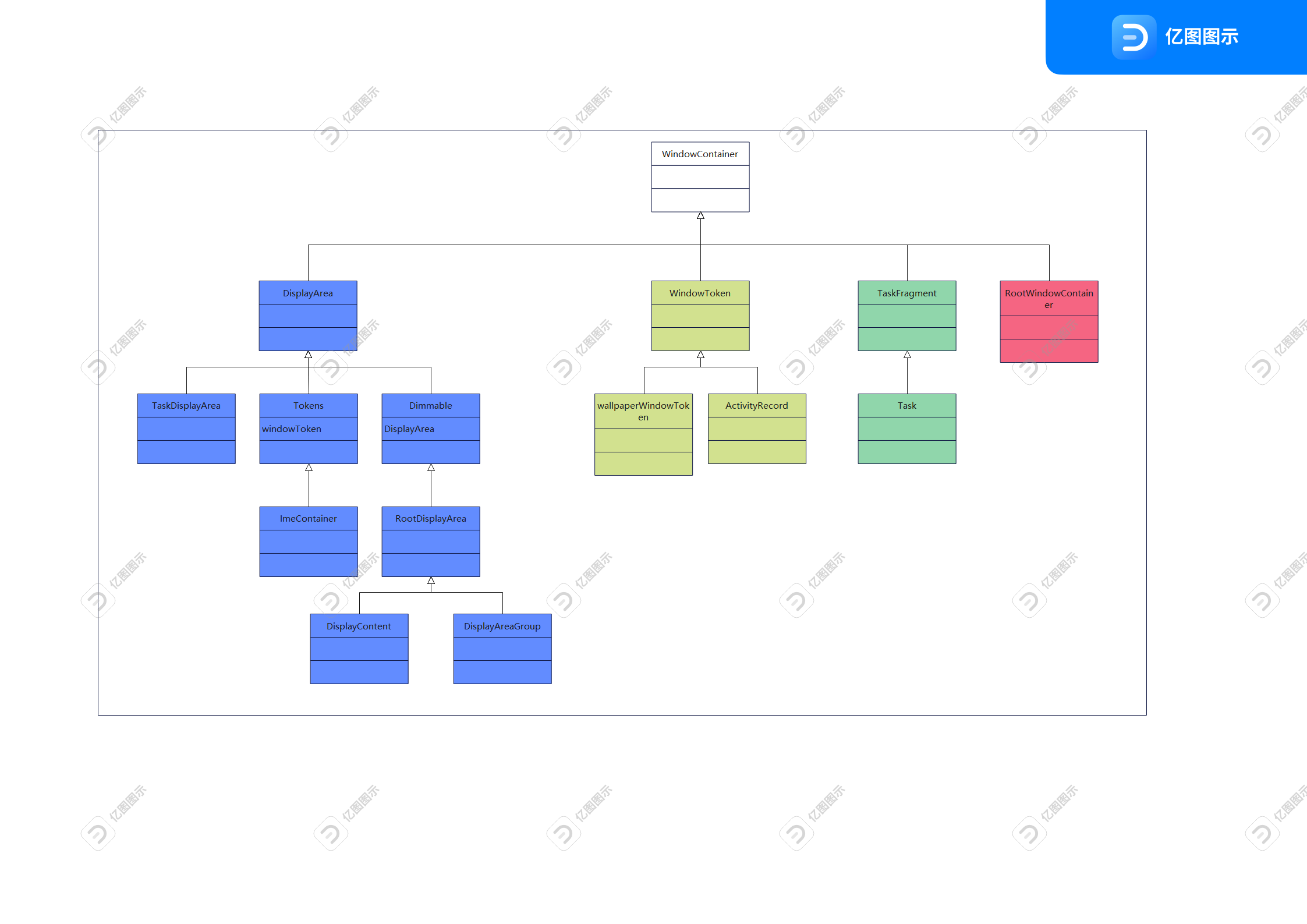
WindowManager相关容器类
窗口中容器类介绍: 本节内容较多,建议结合前面的内容一起阅读: 1、addWindow的宏观概念 2、WindowManager#addView_1 3、WindowManager#addView_2 1)、WindowContainer: class WindowContainer<E extends WindowC…...
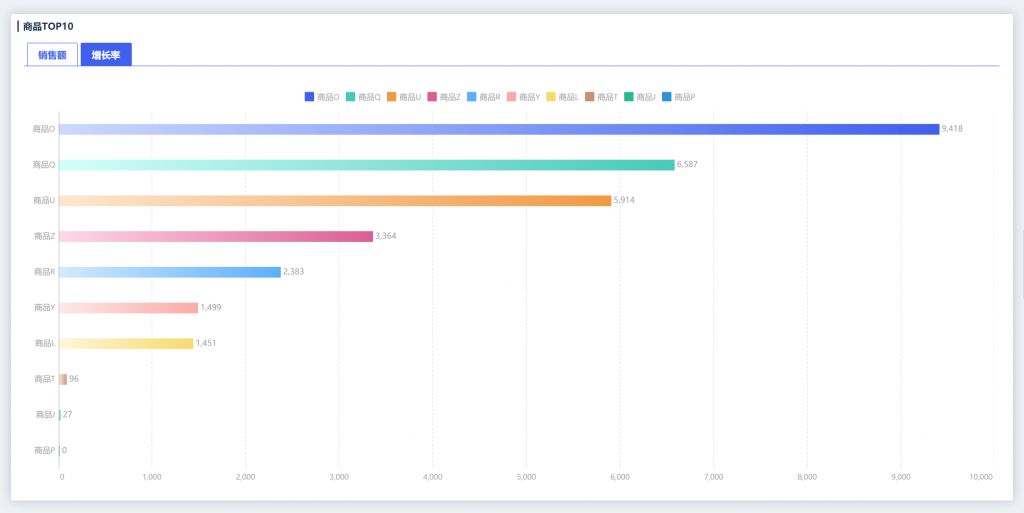
零售行业运营有哪些业务场景?详解各业务场景的分析指标和维度
在当今这个数字化迅速发展的时代,零售行业正经历着前所未有的变革。传统的零售模式正在被新兴的技术和创新的业务场景所颠覆,消费者的需求和购物习惯也在不断地演变。零售行业的运营,作为连接消费者、产品和市场的关键环节,对于零…...

无锡哲讯携手SAP,赋能装备制造业数字化转型
在当今快速发展的工业4.0时代,装备制造业作为国民经济的重要支柱,正面临着前所未有的机遇与挑战。无锡哲讯智能科技有限公司凭借其深厚的行业经验和专业的SAP实施能力,为装备制造业提供全面的数字化解决方案,助力企业实现智能化、…...
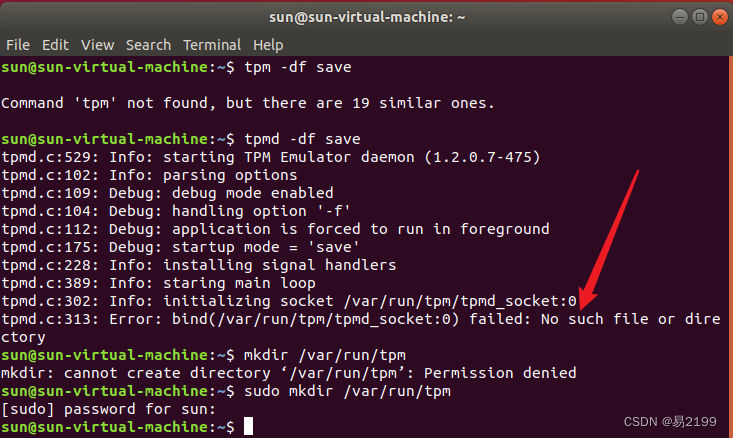
TPM仿真环境搭建
文章目录 背景及注意事项一、CMake二、m4三、GNU MP Library四、TPM_Emulator五、TSS协议栈(trousers-0.3.14.tar.gz)六、 tpm-tools七、查看是否安装成功八、测试 TPM环境(需要开三个终端分别运行)8.1 启动TPM (第一个…...
:使用Processing创作互动艺术:从灵感到实现)
提高篇(五):使用Processing创作互动艺术:从灵感到实现
提高篇(五):使用Processing创作互动艺术:从灵感到实现 引言 互动艺术将观众从被动的观察者转变为主动参与者,通过创意编程和技术手段,让艺术品具备感知和回应的能力。Processing作为一种强大的创意编程工具,提供了丰富的功能和灵活的编程环境,帮助艺术家和设计师实现他…...

华为od-C卷100分题目-3用连续自然数之和来表达整数
华为od-C卷100分题目-3用连续自然数之和来表达整数 题目描述 一个整数可以由连续的自然数之和来表示给定一个整数,计算该整数有几种连续自然数之和的表达式,且打印出每种表达式 输入描述 一个目标整数T(1<T<1000) 输出描述 该整数的所有表达…...

Chrome 自动执行 JS 脚本 | Tampermonkey 插件
文章目录 第 1 步:安装插件 Tampermonkey第 2 步:固定到工具栏第 3 步:在网站上启用 Tampermonkey第 4 步:查看效果第 5 步:调试 JS 代码😂 背景:有个网站,每次进去都要点 3 次才能把相关页面展开。而且,页面经常会自己刷新,导致展开的页面又收回去了。【这一天天的…...

ffmplay 源码解读
stream_open 讲解 // 定义一个静态函数用于初始化并返回VideoState结构体指针,用于管理播放状态 static VideoState* stream_open(const char* filename, AVInputFormat* iformat) {VideoState* is; // 创建VideoState结构体指针// 分配内存并初始化VideoState结构…...

java web如何调用py脚本文件
Controller public class IndexController {RequestMapping("/pythonTest")ResponseBodypublic String pythonTest(){// 假设你的Python脚本名为script.pyString pythonScriptPath "D:\\project\\c1\\hello.py";ProcessBuilder processBuilder new Proce…...

K8s:无状态
无状态服务 无状态服务是指服务的实例之间没有持久化状态,每个实例都是相同的,可以互换使用。 调度器 ReplicationController 简称 RC是 Kubernetes 早期版本中用来确保 Pod 副本始终运行的 API 对象。它通过监控 Pod 副本的数量,确保任何…...
-- 使用 Maven 插件 构建 Docker 镜像)
Docker 入门篇(九)-- 使用 Maven 插件 构建 Docker 镜像
在这篇教程中,我们将学习如何使用 Maven 插件为 Spring Boot 应用构建 Docker 镜像。我们将使用 spring-boot-maven-plugin 和 dockerfile-maven-plugin 这两个插件。 一、前提条件 已安装 Docker。已安装 JDK 8 或以上版本。已安装 Maven。 二 创建一个 Spring …...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
