Matplotlib常见图汇总
Matplotlib是python的一个画图库,便于数据可视化。
安装命令
pip install matplotlib常用命令:
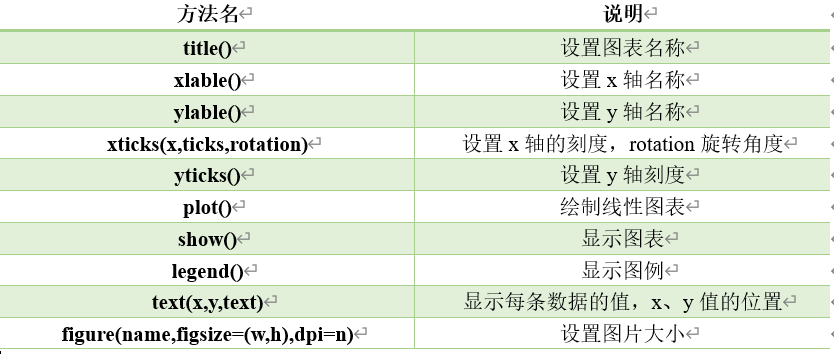
绘制直线,连接两个点
import matplotlib.pyplot as plt
plt.plot([0,5],[2,4])
plt.show()运行结果如下:
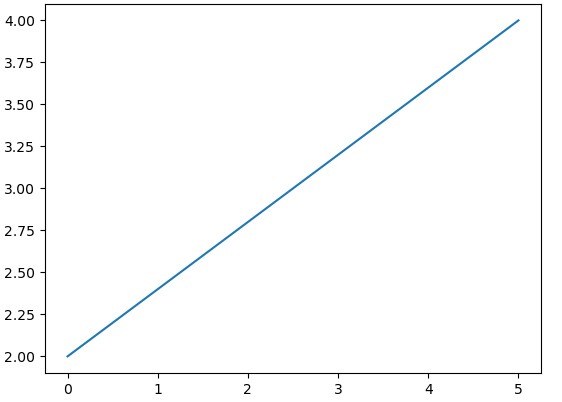
多条线:
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(0,10,100)
plt.plot(x,x+0,'--g',label='--g')
plt.plot(x,x+1,'-.r',label='-.r')
plt.plot(x,x+2,':b',label=':b')
plt.plot(x,x+4,'.k',label='.k')
plt.plot(x,x+5,'*m',label='*m')
plt.legend(loc='upper left',fancybox=True,framealpha=1,shadow=True,borderpad=1)#图例位置,默认左上角,lower right右下角
plt.show()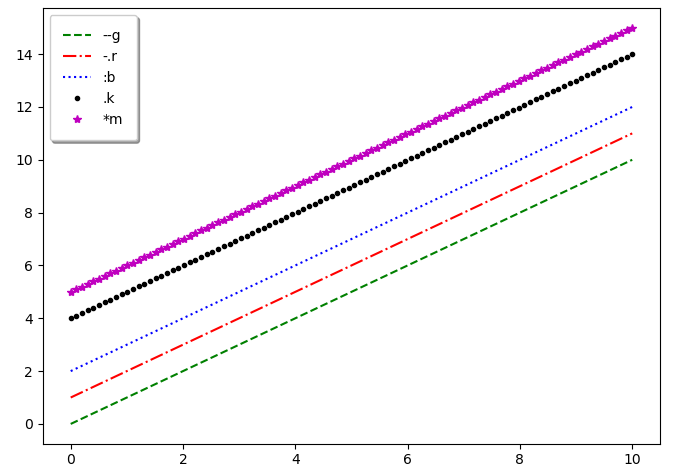
绘制折线:
import matplotlib.pyplot as plt
x = [1, 2, 3, 4, 5, 6]
y = []
for i in range(0, len(x)):y.append(x[i] ** 2)
print()
plt.plot(x,y)
plt.show()运行结果如下:
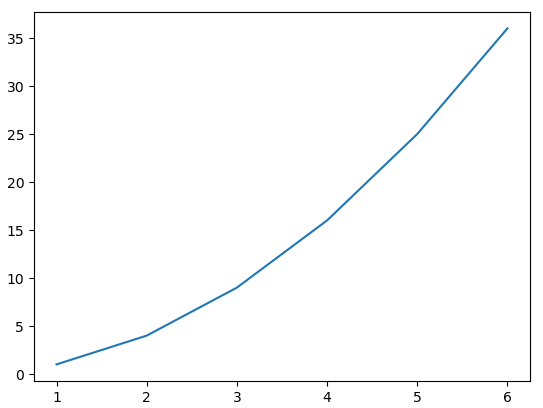
设置样式
import matplotlib.pyplot as plt
x = [1, 2, 3, 4, 5, 6]
y = []
for i in range(0, len(x)):y.append(x[i] ** 2)
print()
plt.plot(x,y,linewidth=5)
plt.rcParams['font.sans-serif']=['SimHei']
plt.xlabel('X')
plt.ylabel('X的平方')
plt.title('折线图绘制')
plt.show()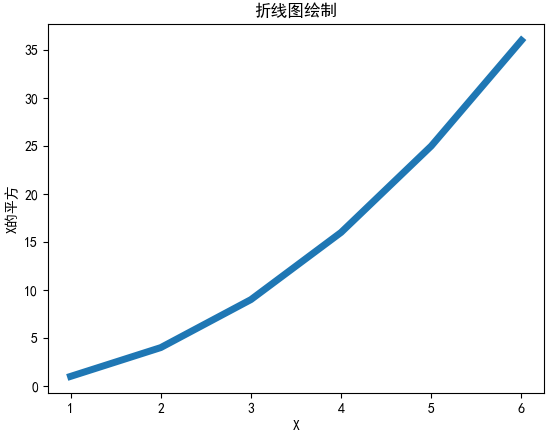
绘制曲线:
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(0,10,100)
sin_y=np.sin(x)
cos_y=np.cos(x)
plt.plot(x,sin_y)
plt.plot(x,cos_y)
plt.show()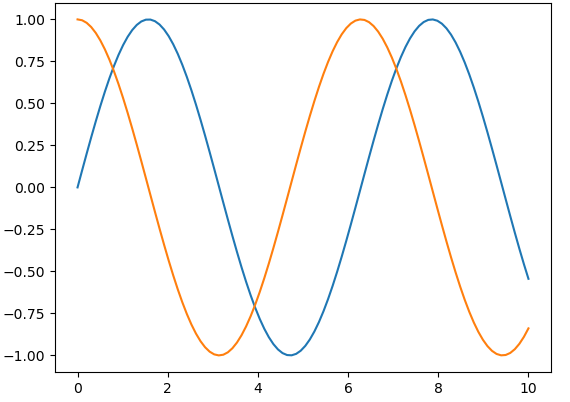
分区
plt.subplot(1,2,1)
plt.plot(x,sin_y)
plt.subplot(1,2,2)
plt.plot(x,cos_y)
plt.show()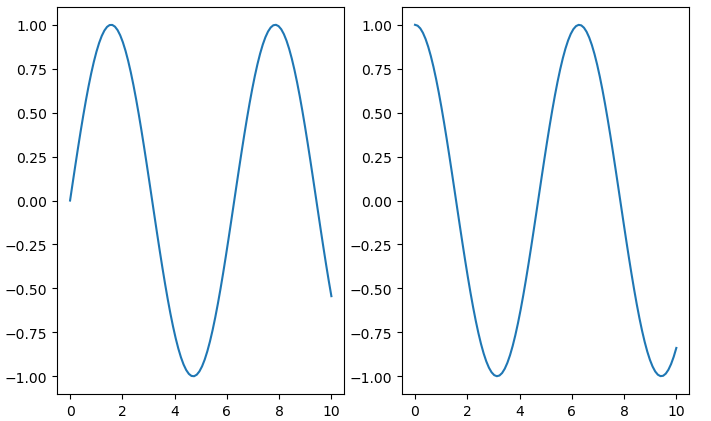
绘制散点图
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
x=np.random.rand(100)
y=np.random.rand(100)
#10size
size=np.random.rand(100)*1000
#100color
color=np.random.rand(100)
plt.scatter(x,y,s=size,c=color,alpha=0.7)#alpha透明度
plt.show()运行结果如下:
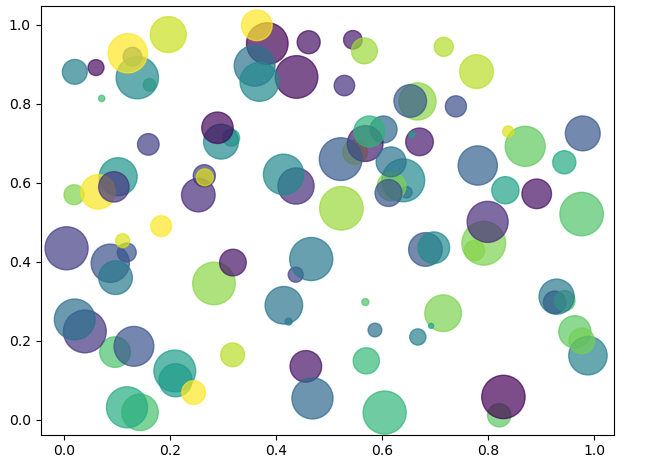
条形图
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
x=[1995,2000,2005,2010,2015,2020]
x_label=['1995年','2000年','2005年','2010年','2015年','2020年']
y=[100,200,300,400,300,200]
plt.bar(x,y,width=3)
plt.xticks(x,x_label)
plt.xlabel('年份')
plt.ylabel('销量')
plt.show()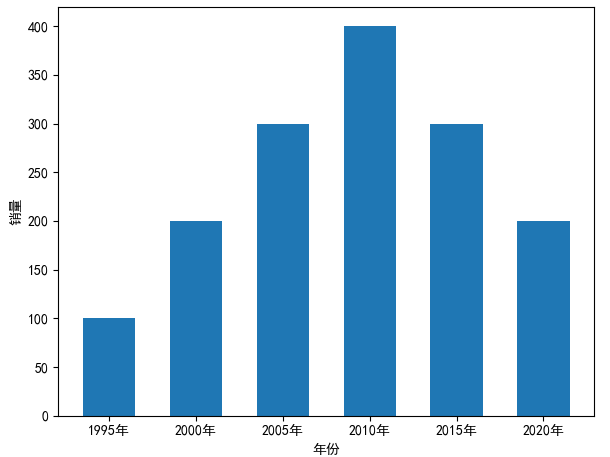
横向的条形图:
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
x=np.arange(6)
y=np.random.randint(-5,5,6)
v_bar=plt.barh(x,y,color='blue')
for bar,height in zip(v_bar,y):if height<0:bar.set(color='green')
plt.axvline(0)
plt.show()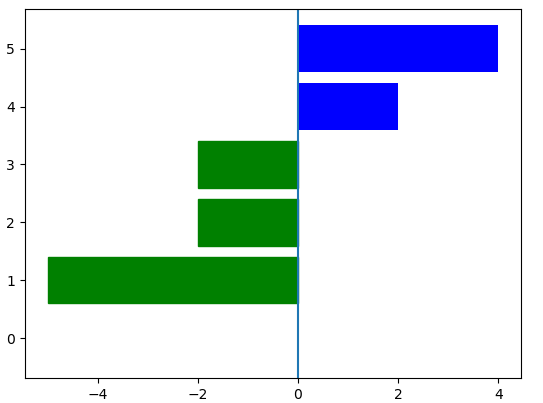
柱状图组合
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
real_names=['熊大','熊二','熊三']
real_num1=[7548,4013,1673]
real_num2=[5453,3840,1980]
real_num3=[1348,2345,1890]
x=np.arange(len(real_names))
width=0.3
plt.bar(x,real_num1,alpha=0.5,width=width,label=real_names[0])
plt.bar([i+width for i in x],real_num2,alpha=0.5,width=width,label=real_names[1])
plt.bar([i+2*width for i in x],real_num3,alpha=0.5,width=width,label=real_names[2])
x_label=['第{}天'.format(i+1) for i in x]
plt.xticks([i+width for i in x],x_label)
plt.title('柱状图组合')
plt.ylabel('数量')
plt.legend()
plt.show()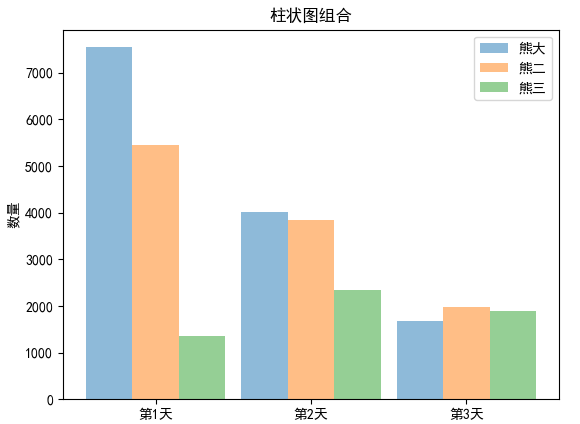
绘制直方图:
import numpy as np
import matplotlib.pyplot as plt
x=np.random.normal(0,1,1000)
y=np.random.normal(-2,1,1000)
z=np.random.normal(3,2,1000)
kwargs=dict(bins=100,alpha=0.5)
plt.hist(x,**kwargs)
plt.hist(y,**kwargs)
plt.hist(z,**kwargs)
plt.show()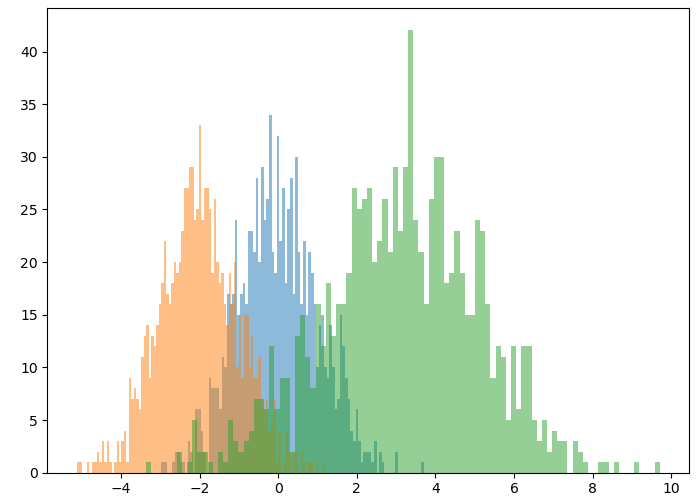
饼图:
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
values = [15, 30, 45, 10]
total = sum(values)
sizes = [v / total for v in values]
labels = ['类别1', '类别2', '类别3', '类别4']
fig, ax = plt.subplots()
ax.pie(sizes, labels=labels, autopct='%1.1f%%', startangle=90)
ax.axis('equal')
plt.show()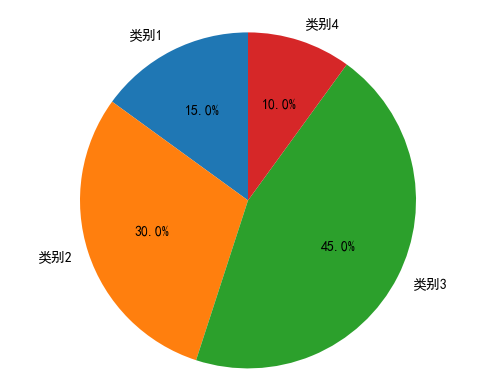
等高线图:
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(-10,10,100)
y=np.linspace(-10,10,100)
X,Y=np.meshgrid(x,y)
Z=np.sqrt(X**2+Y**2)
plt.contourf(X,Y,Z)
#plt.contour(X,Y,Z) #不填充的
plt.show()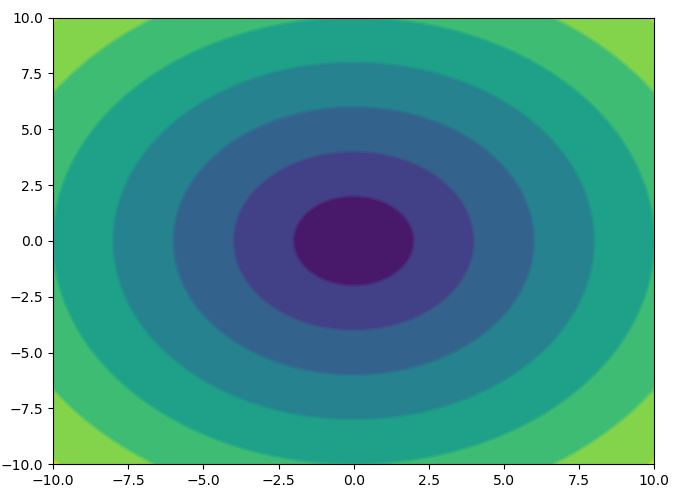
三维图形:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
X=[1,1,2,2]
Y=[3,4,4,3]
Z=[1,100,1,1]
triangles = [[0, 1, 2]]
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_trisurf(X, Y, Z, triangles=triangles, cmap='viridis')
plt.show()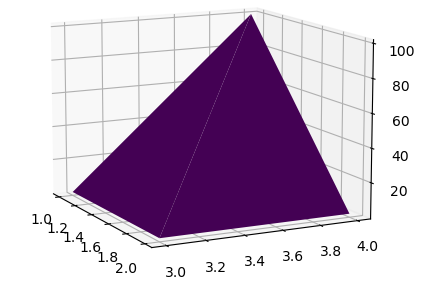
相关文章:

Matplotlib常见图汇总
Matplotlib是python的一个画图库,便于数据可视化。 安装命令 pip install matplotlib 常用命令: 绘制直线,连接两个点 import matplotlib.pyplot as plt plt.plot([0,5],[2,4]) plt.show() 运行结果如下: 多条线:…...
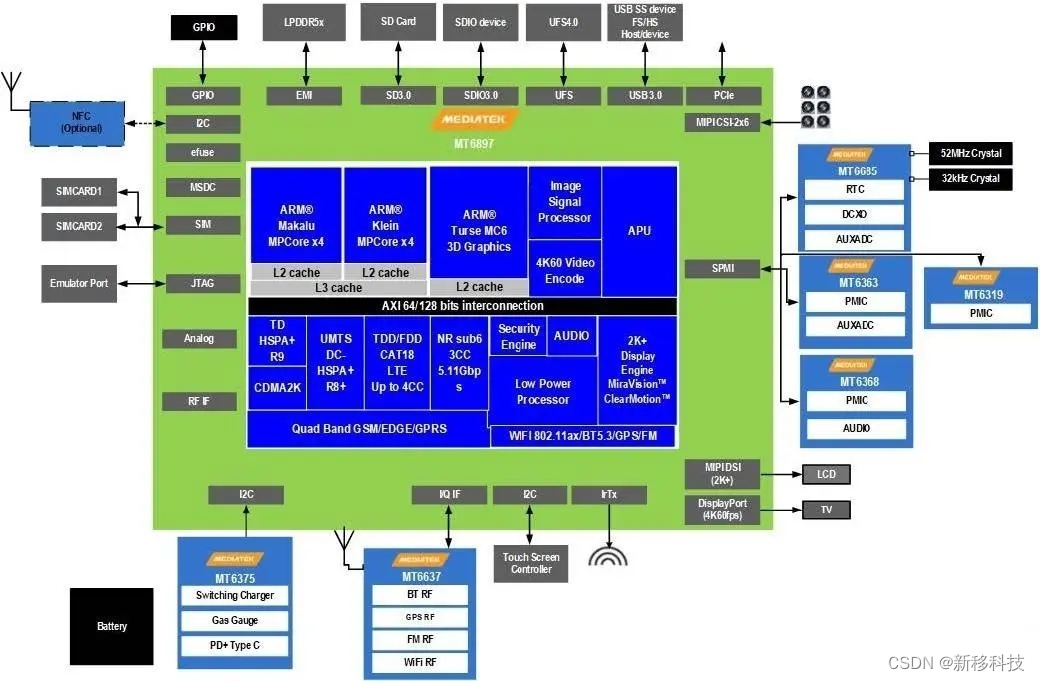
MTK联发科MT6897(天玑8300)5G智能移动处理器规格参数
天玑 8300 采用台积电第二代 4nm 制程,基于 Armv9 CPU 架构,八核 CPU 包含 4 个 Cortex-A715 性能核心和 4 个 Cortex-A510 能效核心,CPU 峰值性能较上一代提升 20%,功耗节省 30%。 此外,天玑 8300 搭载 6 核 GPU Mal…...
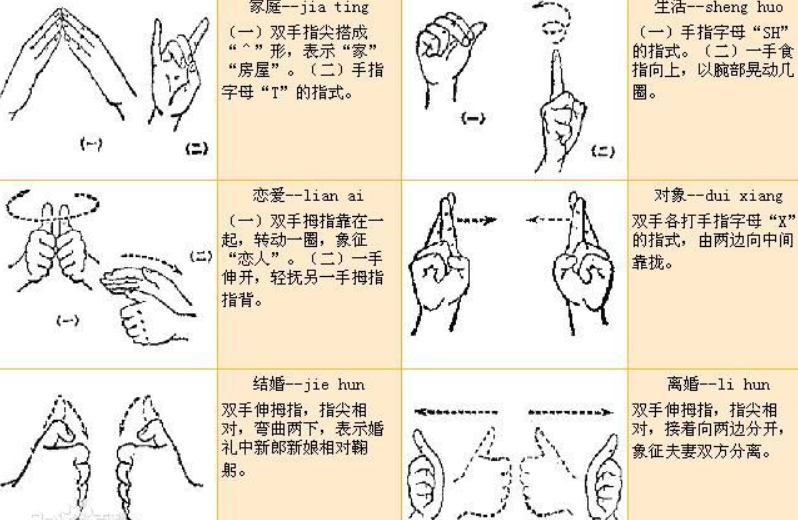
【AIoT-Robot】3d hand pose
手语是聋哑人士的主要沟通工具,它是利用手部和身体的动作来传达意义。虽然手语帮助它的使用者之间互相沟通,但聋哑人士与一般人的沟通却十分困难,这个沟通障碍是源于大部分人不懂得手语。 1. 手势&&手语 手势:手的姿势 ,通常称作手势。它指的是人在运用手臂时,所…...
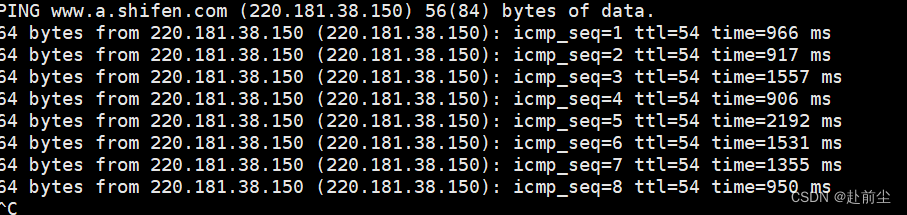
使用 tc (Traffic Control)控制网络延时
设置网络延时 1500ms 800ms tc qdisc add dev eth0 root netem delay 1500ms 800msping 测试 ping www.baidu.com取消设置网络延时 sudo tc qdisc del dev eth0 root...

android原生TabLayout之自定义指示器效果
“com.google.android.material.tabs.TabLayout” 这个玩意说起来大家都不陌生。结合viewPager或者单独使用。场景非常多。当然市面上的三方也数不胜数。但是毕竟是亲儿子。用起来终归是顺手一些。下面说一下TabLayout的具体用法细节: 首先,xml布局引入…...
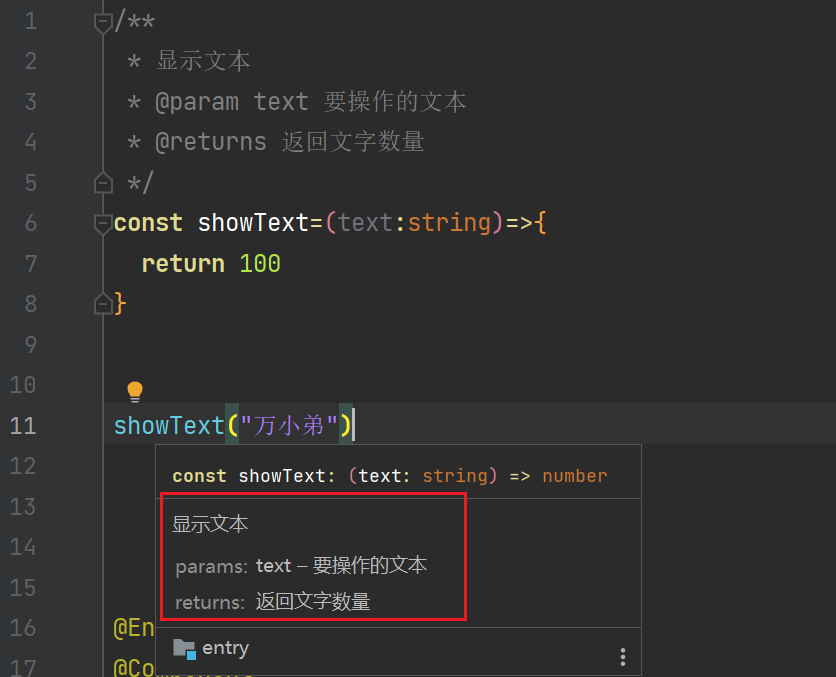
最新 HUAWEI DevEco Studio 使用技巧
最新 HUAWEI DevEco Studio 使用技巧 HUAWEI DevEco Studio 作为我们 harmonyos 应用的开发工具,有必要好好打磨一下。 Chinese(Simplified) 中文汉化插件 GitToolBox 编辑器中显示git历史 保存时自动格式化 写了一堆代码,当保存时,自动帮…...

开源大模型与闭源大模型浅析
引言 技术发展背景 早期语言模型 预训练与微调的范式 开源与闭源模型的兴起 当前的技术前沿 未来发展趋势 开源大模型的特点与优势 技术共享与创新加速 成本效益 社区驱动的发展 透明度和可审计性 促进教育与人才培养 灵活性和自定义 闭源大模型的特点与优势 商…...

docker 命令 ps,inspect,top,logs详解
docker常用命令教程-4 docker ps docker ps 命令用于列出当前正在运行的容器。默认情况下,它只显示正在运行的容器,但你可以使用 -a 或 --all 选项来显示所有容器(包括已停止的容器)。 常用的选项和示例: -a 或 --…...

Windows 找不到文件‘shell:sendto‘。请确定文件名是否正确后,再试一次
执行“shell:sendto”命令的时候,报错:Windows 找不到文件’shell:sendto’。请确定文件名是否正确后,再试一次 解决办法: 在桌面新建一个记事本文件命名为fix.reg,注意后缀是reg,文件中填写以下内容&…...

【算法】模拟算法——外观数组(medium)
题解:模拟算法——外观数组(medium) 目录 1.题目2.题解3.参考代码4.总结 1.题目 题目链接:LINK 2.题解 首先应该理解题意: 就是开始给你一个字符串,然后你对其进行描述。 描述规则是:连续的数字为一组,…...

2024年会计、金融与工商管理国际会议(ICAFBA 2024)
2024年会计、金融与工商管理国际会议 2024 International Conference on Accounting, Finance, and Business Administration 【1】会议简介 2024年会计、金融与工商管理国际会议是一场集合了全球会计、金融与工商管理领域专家学者的学术盛会。此次会议旨在深入探讨会计、金融与…...
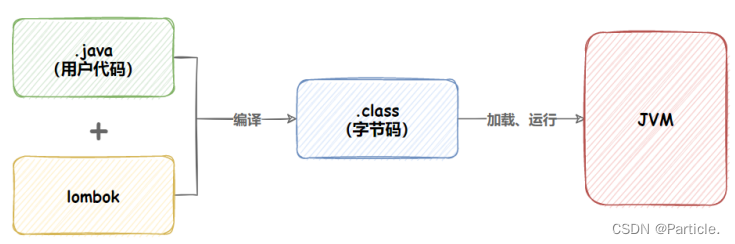
关于 spring boot 的 目录详解 和 配置文件 以及 日志
目录 配置文件 spring boot 的配置文件有两种格式,分别是 properties 和 yml(yaml)。这两种格式的配置文件是可以同时存在的,此时会以 properties 的文件为主,但一般都是使用同一种格式的。 格式 properties 语法格…...

如何删除电脑端口映射?
在使用电脑进行网络连接时,有时需要进行端口映射以实现不同设备之间的信息远程通信。当这些端口映射不再需要时,我们需要及时删除它们以确保网络的安全和稳定。本文将介绍如何删除电脑端口映射的方法。 操作系统自带的工具 大多数操作系统都提供了自带…...
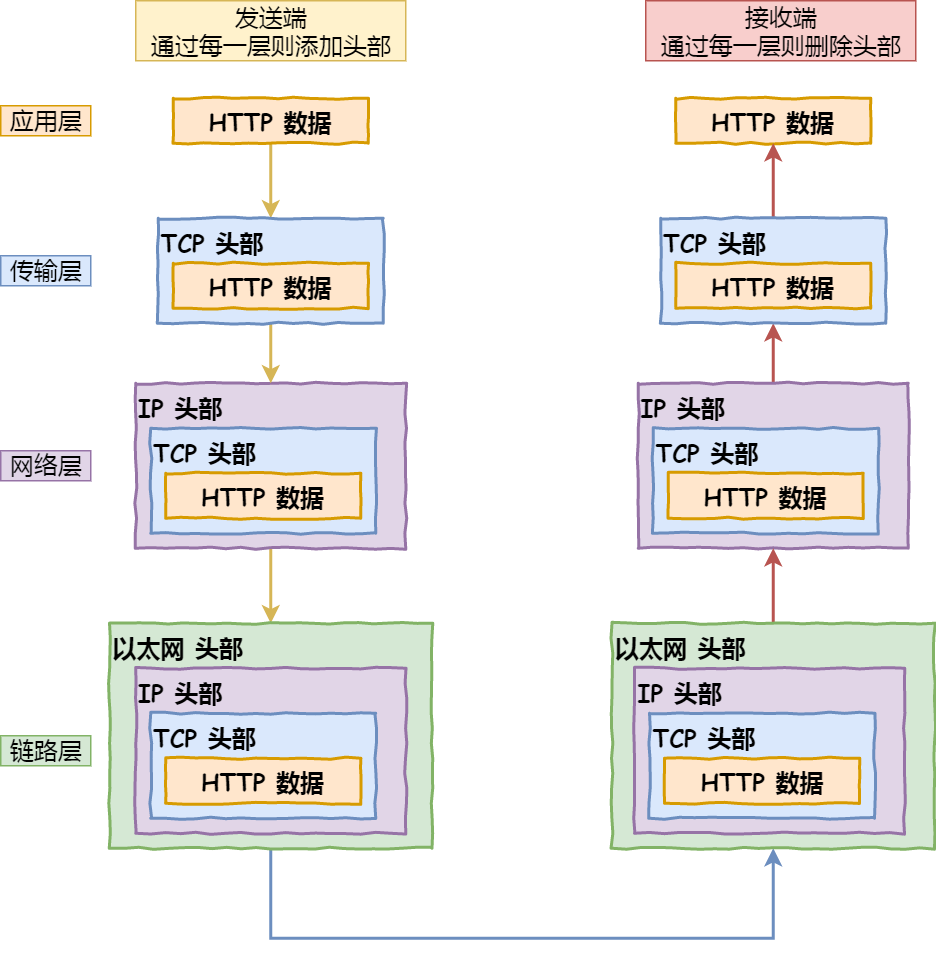
xiaolingcoding 图解网络笔记——基础篇
文章目录 参考一、网络模型有哪几层DMANAPI 机制二、键入网址到网页显示,期间发生了什么?1. HTTP2. DNS3. 协议栈4. TCP5. IP6. MAC7. 网卡8. 交换机9. 路由器10. 服务器 与 客户端的互相扒皮(添加、删除头部信息)参考图HTTP 请求…...
Docker 容器 mysql 配置主从
1、前提条件 集群的条件下 服务器 172.16.11.195 13316:3306 服务器 172.16.11.196 13317:3306 配置好主数据库和从数据 2、配置主从数据库 2.1使用portainer 来管理容器 建立数据库密码 新增配置文件 # mysql-master.cnf [mysqld] server_id110 log-binmysql-binrela…...

64. UE5 RPG 创建新的双手攻击怪物
在上一篇文章中,我们实现了新的功能,现在可以创建多个普通攻击动画,并且可以根据你所使用的普通攻击动画,设置不同的攻击位置。比如,你使用武器,那么攻击位置需要从武器上获取,如果你没有持有武…...

(求一个整数各位数的和)编写程序,读取一个在0和1000之间的整数,并将该整数的各位数字相加。例如:整数是 932,各位数字之和为14。
(求一个整数各位数的和)编写程序,读取一个在0和1000之间的整数,并将该整数 的各位数字相加。例如:整数是 932,各位数字之和为14。 提示:利用操作符%分解数字,然后使用操作符/去掉分解出来的数字。例如: 932%10-2 932/10-93。下面是一个运行示…...
)
大模型参加高考,同写2024年高考作文,及格分(通义千问、Kimi、智谱清言、Gemini Advanced、Claude-3-Sonnet、GPT-4o)
大家好,我是章北海 今天高考,上午的语文结束,市面上又要来一场大模型参考的文章了。 我也凑凑热闹,让通义千问、Kimi、智谱清言一起来写一下高考作文。 公平起见,不加任何其他prompt,直接把题目甩过去。…...
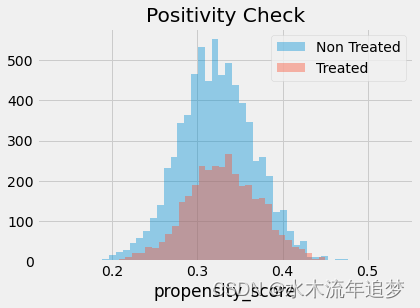
【因果推断python】24_倾向得分2
目录 倾向加权 倾向得分估计 倾向加权 好的,我们得到了倾向得分。怎么办?就像我说过的,我们需要做的就是以此为条件。例如,我们可以运行一个线性回归,它仅以倾向得分为条件,而不是所有的 X。现在ÿ…...
)
部件库(Widget Factory)
部件库(Widget Factory) 部件库,也被称为Widget Factory,是一个强大的工具,用于创建、存储和管理可重用的软件组件。在本文中,我们将深入探讨部件库的概念、重要性、以及如何在现代软件开发中使用它。 什么是部件库? 部件库是一个集合,其中包含了各种预先构建的软件…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
