2024.6.8
2024.6.8
**每日一题**
3040.相同分数的最大操作数目 Ⅱ,通多题意可知,该题最多有三种操作分数,分别是前两个,最后两个,以及第一个和最后一个的和。从这里也可以看出一共有三种状态转移方式,所以我们可以利用DP或者记忆化搜索的方式来求解。对三种操作分数分别求最大次数,再求他们的最大值。依次判断三个状态,当前区间的前面两个,最后两个,以及第一个和最后一个,直到遍历区间长度为1就可以求出整个区间的答案。
516.最长回文子序列,该题是一个区间求最值问题,我们自然地想到可以通过小区间转移到大区间来进行求解,状态转移就对应着动态规划或者搜索算法。在本题中我们使用DP思想,从尾部开始遍历字符串,对于每个字符再遍历它之后的元素,一共有三种状态,当i==j时,令数组为1;当s[i]==s[j]时,我们还要分情况讨论,如果i==j-1,此时直接令数组为2,因为下一个状态i>j;如果i!=j-1,那么f[i][j]=f[i+1][j-1]+2;
最后一种情况是,当两个字符不构成回文子串时,我们选择上一个状态下最大的一端继续前进,
f[i][j]=max(f[i+1][j],f[i][j-1]);
相关文章:

2024.6.8
2024.6.8 **每日一题** 3040.相同分数的最大操作数目 Ⅱ,通多题意可知,该题最多有三种操作分数,分别是前两个,最后两个,以及第一个和最后一个的和。从这里也可以看出一共有三种状态转移方式,所以我们可以利…...
室内外融合定位是如何做到成为定位领域的新宠
在信息化高速发展的今天,定位技术已成为人们生活和工作中不可或缺的一部分。随着物联网、智慧城市等领域的蓬勃发展,传统的单一定位方式已无法满足复杂多变的环境需求。在这样的背景下,室内外融合定位技术应运而生,以其独特的优势…...

【刷题篇】分治-归并排序
文章目录 1、排序数组2、交易逆序对的总数3、计算右侧小于当前元素的个数4、翻转对 1、排序数组 给你一个整数数组 nums,请你将该数组升序排列。 class Solution { public:vector<int> tmp;void mergeSort(vector<int>& nums,int left,int right){…...
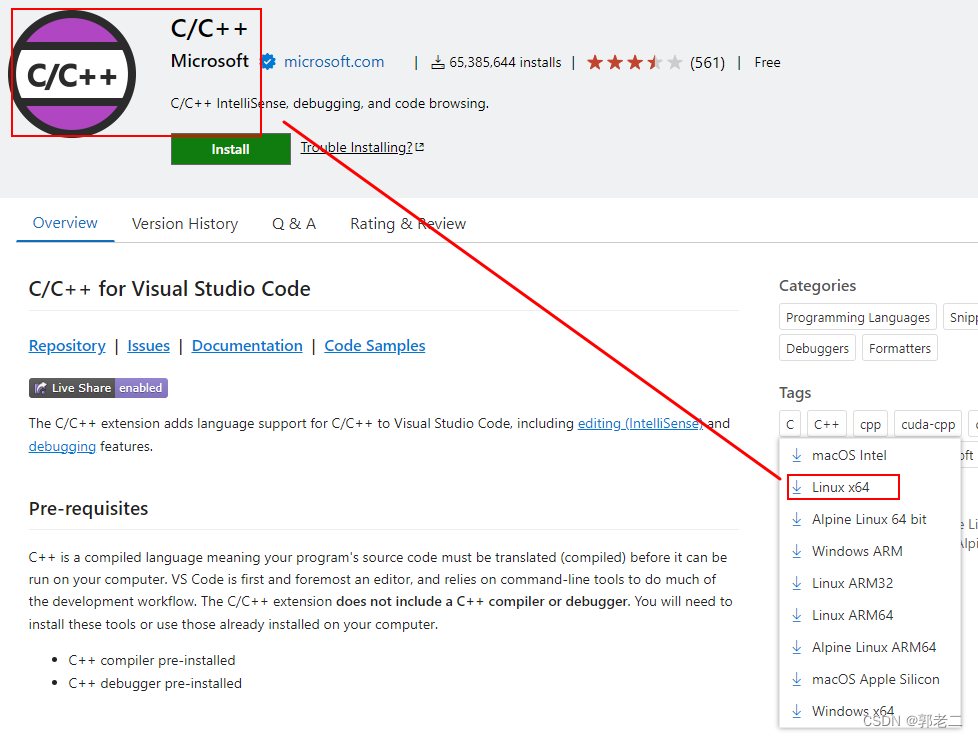
【经验】Ubuntu上离线安装VsCode插件浏览Linux kernel源码
1、下载VsCode离线安装包 1.1 下载 下载地址:https://marketplace.visualstudio.com/vscode 本人安装的插件: C/C++ checkpatch Chinese clangd kconfig Makefile Tools Perl Perl Toolbox注意:C/C++插件要安装Linux 64版本 1.2 安装 将离线安装包拷贝到Ubuntu中,执…...

鼠标侧键映射虚拟桌面切换 —— Win11
鼠标侧键映射虚拟桌面切换 —— Win11 基于 AutoHotkey 实现功能 下载软件 AutoHotkey建议安装在默认路径下(C盘) 此软件非常小,几乎不占用资源软件安装在默认路径以外的位置可能导致部分功能不可用 新建一个 .ahk 文件使用记事本打开该 .a…...

2024全国大学生数据统计与分析竞赛B题【电信银行卡诈骗的数据分析】思路详解
电信诈骗是指通过电话、网络和短信方式,编造虚假信息,设置骗局,对受害人实施远程、非接触式诈骗,诱使受害人打款或转账的犯罪行为,通常以冒充他人及仿冒、伪造各种合法外衣和形式的方式达到欺骗的目的,如冒…...

鸿蒙emitter 订阅事件封装 EmitterUtils
适用于api11 和api12 废话不多说,直接上代码 import emitter from ohos.events.emitter; import { StringUtils } from ohos/flutter_ohos;export class EmitterUtils{/*** 发射字符串类型的* param eventId* param data*/public static sendEvent(eventId:stri…...
)
C语言---深入指针(4)
回调函数 //回调函数就是通过函数指针调用的函数 //这个在之前的转移表-计算器里面很明显,通过函数指针数组内的函数指针进行函数的调用 // // // 将这四段代码分装成一个函数,一个代码将这4个问题都解决 int Add(int x, int y) {return x y; } int S…...
【启程Golang之旅】让文件操作变得简单
欢迎来到Golang的世界!在当今快节奏的软件开发领域,选择一种高效、简洁的编程语言至关重要。而在这方面,Golang(又称Go)无疑是一个备受瞩目的选择。在本文中,带领您探索Golang的世界,一步步地了…...

oracle视图无法删除,orcl视图删除卡住怎么办
话说,这是一个来自周四加班夜晚的故事,当时我的PL/SQL卡住了,每次查询这个表时都会卡住。 经过一番研究,我找到了解决办法,分为三个步骤: 使用以下查询语句获取正在执行的SQL查询的SID和OracleID…...

ug编程怎么录制宏:一步步探索自动化编程的奥秘
ug编程怎么录制宏:一步步探索自动化编程的奥秘 在UG编程的浩瀚领域中,录制宏是一项强大而神秘的功能。它就像一位魔法师,能够将繁琐的重复操作化为简单的指令,释放出惊人的编程效率。然而,对于许多初学者来说…...
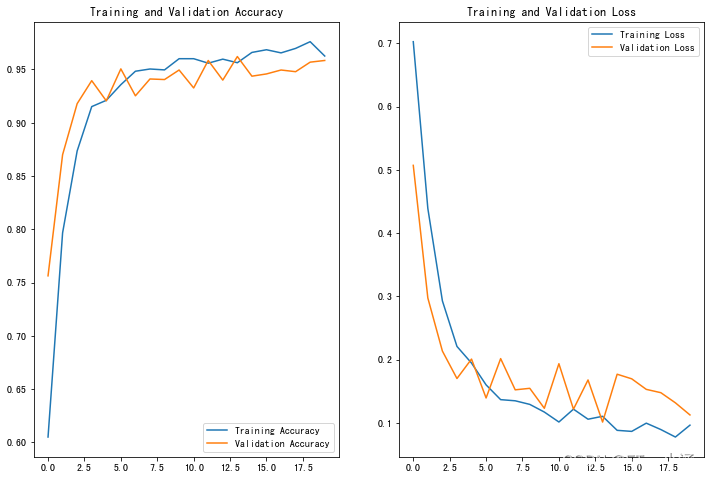
深度学习Week16——数据增强
文章目录 深度学习Week16——数据增强 一、前言 二、我的环境 三、前期工作 1、配置环境 2、导入数据 2.1 加载数据 2.2 配置数据集 2.3 数据可视化 四、数据增强 五、增强方式 1、将其嵌入model中 2、在Dataset数据集中进行数据增强 六、训练模型 七、自定义增强函数 一、前言…...

python-自幂数判断
[题目描述]: 自幂数是指,一个N 位数,满足各位数字N 次方之和是本身。例如,153153 是 33 位数,其每位数的 33 次方之和,135333153135333153,因此 153153 是自幂数;16341634 是 44 位数…...
RocketMQ教程(三):RocketMQ的核心组件
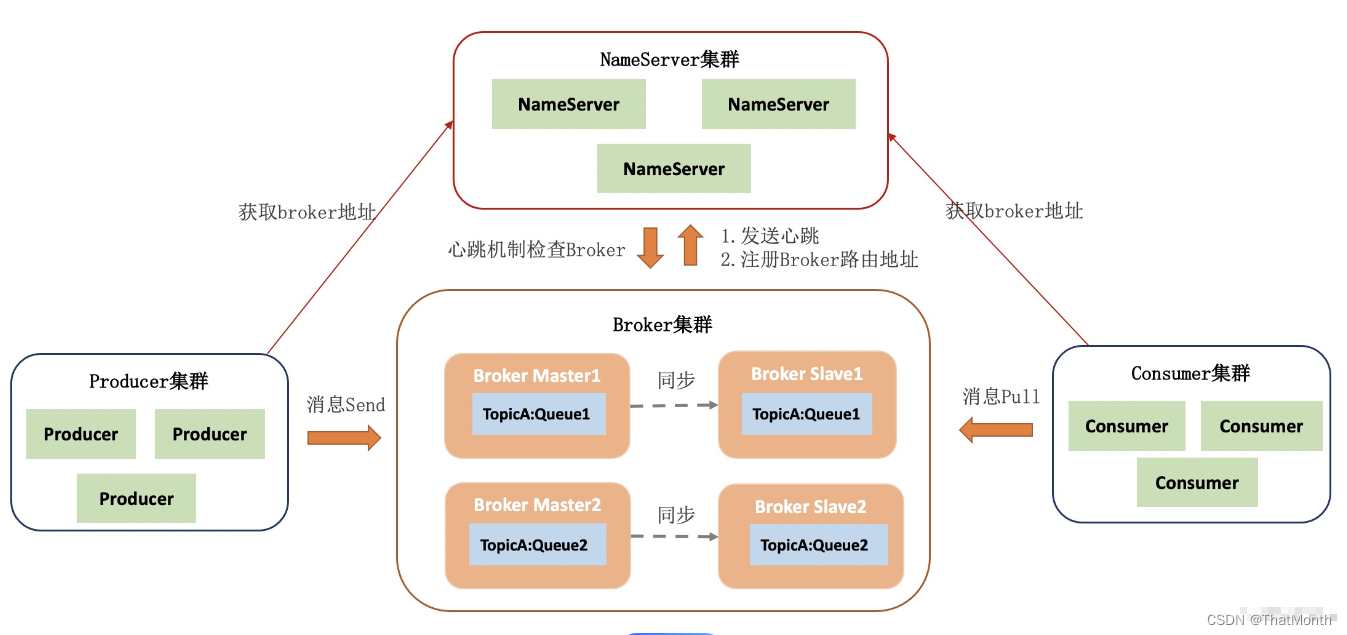
四个核心组件 RocketMQ 的架构采用了典型的分布式系统设计理念,以确保高性能、高可用和可扩展性。RocketMQ 主要由四个核心组件构成:NameServer、Broker、Producer 和 Consumer。下面是对这些组件以及它们在 RocketMQ 中的角色和功能的概述: 1. NameServer 角色和功能:Name…...

46.SQLserver中按照多条件分组:查询每个地方的各种水果的种植数量,新增时,一个地方同时有几种水果,只插入一条记录,同时多种水果之间使用|隔开
1.SQLserver中按照多条件分组 ,分组条件包括(一个字段使用|进行分割,如:apple|orange,查询时,apple和orange分别对应一条数据) 例如:SQL如下: SELECT FROM ( SELECT CDFBM 地方编码…...
C盘满了怎么办,Windows11的C盘没有磁盘清理选项怎么办,一次搞定
问题: 太久没清电脑了,满的跟垃圾堆一样。。。C盘红色看上去很不妙。 一. C盘满了怎么办: 1. 删除临时文件 找到 C:\Windows\Temp,进入Temp资料夹,选中所有文件夹和文件,按下ShiftDelete键,彻…...

「动态规划」当小偷改行去当按摩师,会发生什么?
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),…...

Python | 排队取奶茶
队列的基本概念(队头、队尾)和特点(先入先出) 在 Python 语言中,标准库中的queue模块提供了多种队列的实现,比如普通队列和优先级队列,因此你可以使用queue.Queue类来创建队列,不过…...
mysql当前状态分析(show status)
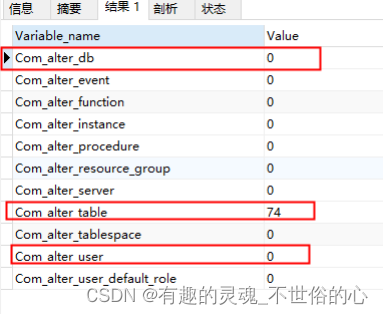
文章目录 查看当前线程数据查询连接情况查询缓存相关查询锁相关查询增删改查执行次数查询DDL创建相关 SHOW STATUS 是一个在 MySQL 中用来查看服务器运行状态的命令。它可以帮助你了解服务器的当前性能,包括连接数、表锁定、缓冲区使用情况等信息。 查看当前线程数据…...
——使用机器学习进行金三角大米分布图)
Google Earth Engine(GEE)——使用机器学习进行金三角大米分布图
第 1 步:转到https://code.earthengine.google.com/打开代码编辑器 第 2 步:使用以下代码从 Google Earth Engine Asset 导入数据 // 导入影像集合 var composites = ee.ImageCollection("projects/servir-mekong/yearlyComposites"); // 导入训练数据 var data …...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
