leetcode 1631.最小体力消耗路径
思路:BFS+二分
这道题和洛谷上的那个“汽车拉力赛”那道题很相似,但是这道题相较于洛谷那个来说会简单一些。
这里作者一开始写的时候思路堵在了怎么在BFS中用二分,先入为主的以为需要先写出来搜索函数然后再去处理二分的事,但是这里是先二分找数,然后再搜索才是对的。所以先入为主之后就没有做出来。
注意:需要注意数据范围,另外,每一次更新mid数值的时候,我们上一次已经搜索过的数组,队列等存储单元都需要清空,不然的话会影响后面的输出结果。还有,二分注意用哪一个模板,选择也是很重要的。这里主要是求最小值,所以是(left+right)/2而不是(left+right+1)/2,还有就是while中不要left<=right,你用范围的二分查找会造成死循环,但是用于基本的找数是可以的。
class Solution {
public:int minimumEffortPath(vector<vector<int>>& heights) {int dx[4]={1,-1,0,0};int dy[4]={0,0,1,-1};int left=0;int right=1000000;while(left<right){queue<pair<int,int>>q;q.push({0,0});vector<vector<bool>>st(heights.size(),vector<bool>(heights[0].size(),false));st[0][0]=true;int mid=(left+right)/2;while(!q.empty()){auto tmp=q.front();q.pop();for(int i=0;i<4;i++){int a=dx[i]+tmp.first;int b=dy[i]+tmp.second;if(a>=heights.size()||a<0||b<0||b>=heights[0].size())continue;if(st[a][b])continue;if(abs(heights[a][b]-heights[tmp.first][tmp.second])>mid)continue;q.push({a,b});st[a][b]=true;}}if(st[heights.size()-1][heights[0].size()-1]){right=mid;}else{left=mid+1;}}return right;}
};相关文章:

leetcode 1631.最小体力消耗路径
思路:BFS二分 这道题和洛谷上的那个“汽车拉力赛”那道题很相似,但是这道题相较于洛谷那个来说会简单一些。 这里作者一开始写的时候思路堵在了怎么在BFS中用二分,先入为主的以为需要先写出来搜索函数然后再去处理二分的事,但是…...

【ARM64 常见汇编指令学习 19.2 -- ARM64 地址加载指令 ADR 详细介绍】
文章目录 地址加载指令 ADRADR 指令使用场景例子注意事项 地址加载指令 ADR ARMv8 架构引入了一系列的改进和扩展,包括对汇编指令集的更新。在这之中,ADR 指令是一个重要的组成部分,它用于计算并加载一个地址到寄存器。 ADR 指令 ADR 指令…...

vscode输出控制台中文显示乱码最有效解决办法
当VSCode的输出控制台中文显示乱码时,一个有效的解决办法是通过设置环境变量来确保编码的正确性。以下是解决方式: 首先,设置环境变量以修正乱码问题: 如果上述方法没有解决乱码问题,请继续以下步骤: 右键…...
springboot + Vue前后端项目(第十五记)
项目实战第十五记 写在前面1.后端接口实现1.1 用户表添加角色字段1.2 角色表增加唯一标识字段1.3 UserDTO1.4 UserServiceImpl1.5 MenuServiceImpl 2. 前端实现2.1 User.vue2.2 动态菜单设计2.2.1 Login.vue2.2.2 Aside.vue 2.3 动态路由设计2.3.1 菜单表新增字段page_path2.3.…...

如何在Windows 11中恢复丢失的快速访问菜单?这里提供解决办法
序言 在电脑的“快速访问”菜单中找不到固定的项目?或者,整个菜单对你来说已经消失了吗?无论哪种方式,你都可以强制你的电脑恢复菜单并显示其中的所有项目。以下是如何在你的Windows 11电脑上做到这一点。 将文件资源管理器设置为打开到主页 当你在文件资源管理器的左侧…...

变声器软件免费版有哪些?国内外12大热门变声器大盘点!(新)
变声软件是一种人工智能AI音频处理工具,允许用户实时修改自己的声音或改变预先录制的音频。这些软件解决方案可提供不同的效果,如改变声音的音调或速度,或将我们的声音转换成其他人或其他东西的声音,如名人、卡通人物、机器人或不…...
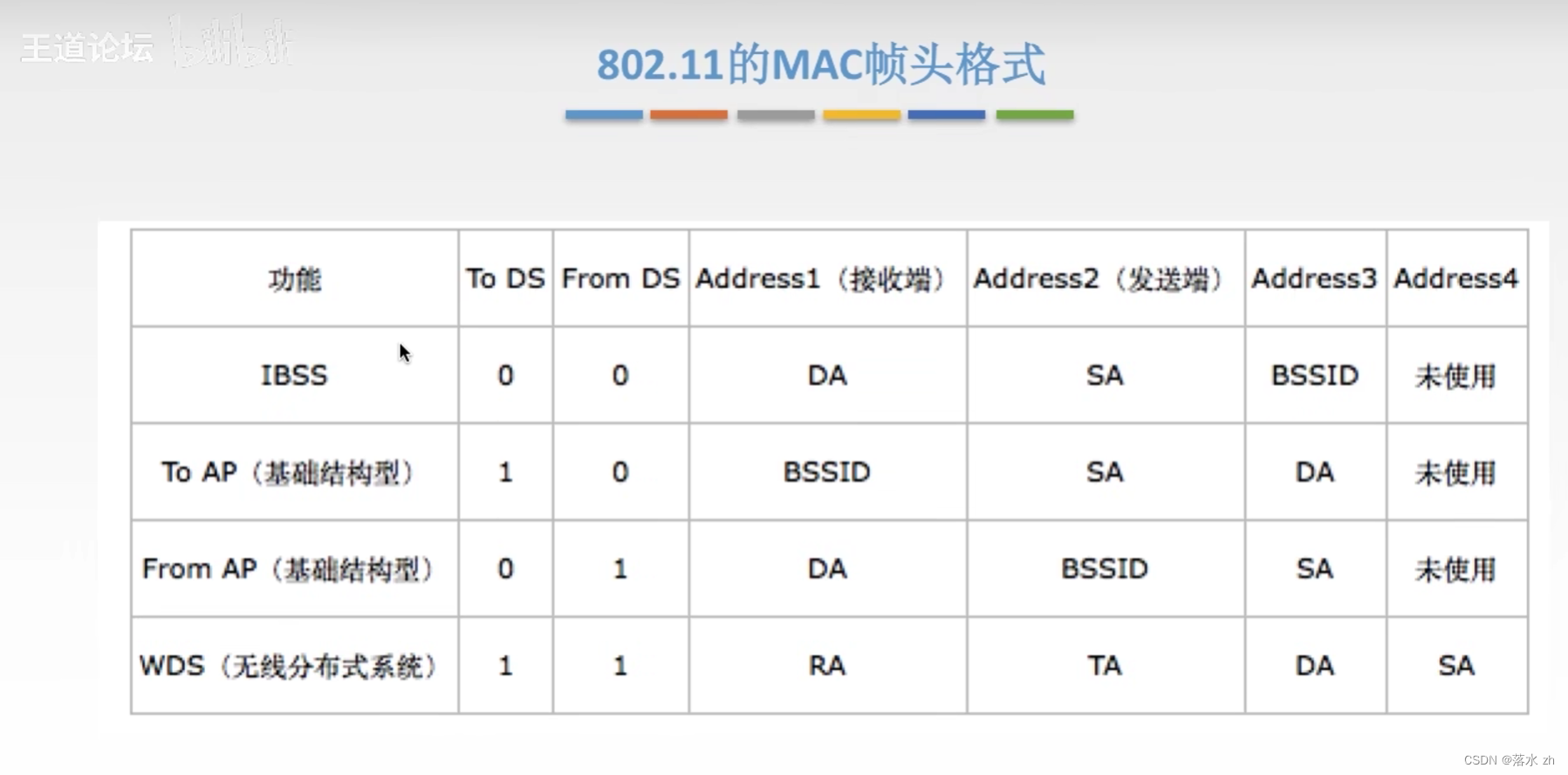
计算机网络 —— 数据链路层(无线局域网)
计算机网络 —— 数据链路层(无线局域网) 什么是无线局域网IEEE 802.11主要标准及其特点: 802.11的MAC帧样式 我们来看看无线局域网: 什么是无线局域网 无线局域网(Wireless Local Area Network,简称WLAN…...

SpringBoot图书管理系统【附:资料➕文档】
前言:我是源码分享交流Coding,专注JavaVue领域,专业提供程序设计开发、源码分享、 技术指导讲解、各类项目免费分享,定制和毕业设计服务! 免费获取方式--->>文章末尾处! 项目介绍048: 图…...

shell简介
一、Shell 概念定义 Shell 是用 C 语言编写的程序,是用户使用 Linux 的桥梁,既是命令语言又是程序设计语言。 shell 脚本为 Shell 编写的脚本程序,常说的 shell 通常指 shell 脚本。 包含一系列命令的文本文件,这些命令按照特定…...
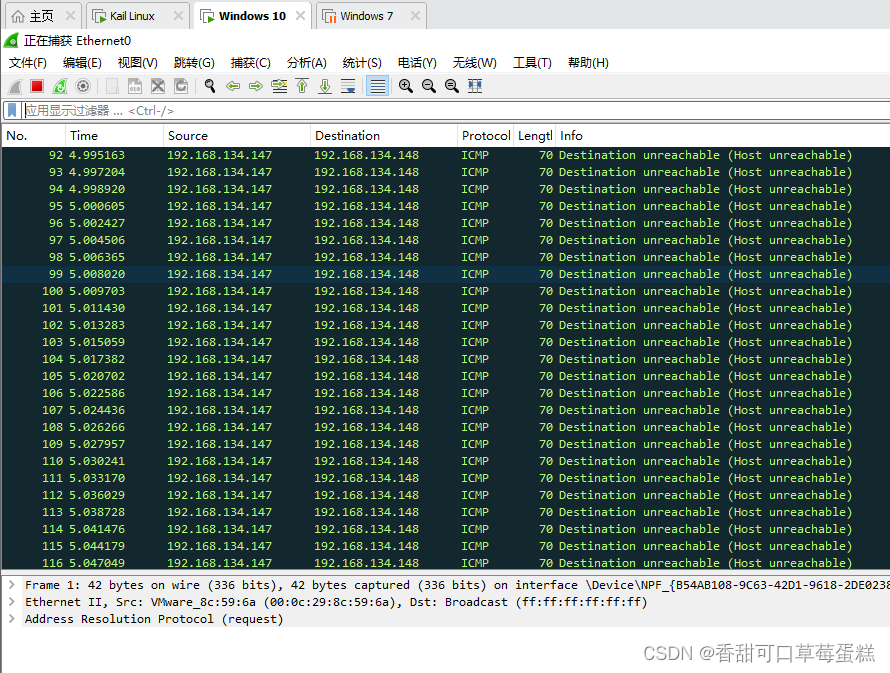
使用 Scapy 库编写 ICMP 不可达攻击脚本
一、介绍 ICMP不可达攻击是一种利用ICMP(Internet Control Message Protocol)不可达消息来干扰或中断目标系统的网络通信的攻击类型。通过发送伪造的ICMP不可达消息,攻击者可以诱使目标系统认为某些网络路径或主机不可达,从而导致…...

Electron qt开发教程
模块安装打包 npm install -g electron-forge electron-forge init my-project --templatevue npm start //进入目录启动 //打包成一个目录到out目录下,注意这种打包一般用于调试,并不是用于分发 npm run package //打出真正的分发包,放在o…...

尝试用 GPT-4o 写 2024高考语文作文
文章目录 新课标I卷科技进步与问题的演变 新课标II卷抵达未知之境:探索与成长的旅程 全国甲卷坦诚交流:构建真正相遇的桥梁 北京卷历久弥新 天津卷定义与自定义:在世界的缤纷中前行 上海卷认可度的思考与反思 新课标I卷 阅读下面的材料&#…...

自动化Reddit图片收集:Python爬虫技巧
引言 Reddit,作为一个全球性的社交平台,拥有海量的用户生成内容,其中包括大量的图片资源。对于数据科学家、市场研究人员或任何需要大量图片资源的人来说,自动化地从Reddit收集图片是一个极具价值的技能。本文将详细介绍如何使用…...

自动驾驶人工智能
自动驾驶技术中使用的算法和滤波器 如何部署软件中的算法和滤波器,以增强传感器数据的可用性和应用性 自动驾驶人工智能 文章目录 一、介绍二、自动驾驶的算法2.1 感知算法2.2 本地化算法2.3 映射算法2.4 规划算法2.5 控制算法2.6 过滤 器2.7 卡尔曼滤波器2.8 颗粒过…...

基础乐理入门
基础概念 乐音:音高(频率)固定,振动规则的音。钢琴等乐器发出的是乐音,听起来悦耳、柔和。噪音:振动不规则,音高也不明显的音。风声、雨声、机器轰鸣声是噪音,大多数打击乐器&#…...

mysql 8 linux7,8安装教程
选择自己对应的linux版本 cat /etc/os-release //查看自己linux系统版本 1.mysql下载地址 MySQL :: Download MySQL Community Server (Archived Versions) 拉到下面找到 选择自己linux指定的版本,否则会很麻烦 cat /etc/os-release //查看系统版本 2.查…...
通俗解释!)
『矩阵论笔记』特征分解(eigendecomposition)通俗解释!
特征分解(eigendecomposition)通俗解释! 文章目录 一. 特征分解(eigendecomposition)通俗解释!1. 它是如何工作的2. 试图达到什么目的3. 为什么它有用(将一个方阵分解成这三个组成矩阵有什么好处呢?)二. 参考文献一. 特征分解(eigendecomposition)通俗解释! 大家好,欢迎回…...

顶级域名和二级域名的区别
互联网是一个由无数个网络节点组成的复杂系统,而域名则是这个系统中用于识别和定位这些节点的重要工具。在域名体系中,顶级域名(Top-Level Domain,TLD)和二级域名(Second-Level Domain,SLD)是两个基本的层级概念。本文将探讨这两者…...

深入解析Kafka消息丢失的原因与解决方案
深入解析Kafka消息丢失的原因与解决方案 Apache Kafka是一种高吞吐量、分布式的消息系统,广泛应用于实时数据流处理。然而,在某些情况下,Kafka可能会出现消息丢失的情况,这对于数据敏感的应用来说是不可接受的。本文将深入解析Ka…...

【Python列表解锁】:掌握序列精髓,驾驭动态数据集合
文章目录 🚀一、列表🌈二、常规操作💥增💥删💥改💥查 ⭐三、补充操作 🚀一、列表 列表是一个能够存储多个同一或不同元素的序列 列表:list ---- [] 列表属于序列类型(容器…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
