19、matlab信号预处理中的中值滤波(medfilt1()函数)和萨维茨基-戈雷滤波滤(sgolayfilt()函数)
1、中值滤波:medfilt1()函数
说明:一维中值滤波
1)语法
语法1:y = medfilt1(x) 将输入向量x应用3阶一维中值滤波器。
语法2:y = medfilt1(x,n) 将一个n阶一维中值滤波器应用于x。
语法3:y = medfilt1(x,n,[],dim) 指定过滤器操作的维度dim。
2)参数说明
x:输入信号 y:输出信号 dim:筛选维度
3)NaN(信号数据缺失)处理
'includenan' :返回过滤信号,以便包含NaN的任何段的中值也是NaN。
'omitnan' 返回过滤后的信号,使得包含 NaN 的任何段的中值为非 NaN 值的中值。如果一个段的
所有元素都是 NaN,则结果为 NaN终点过滤,指定为'零填充'或'截断'。
'zeropad' 在端点之外,信号被视为零。 'truncate' 在接近信号边缘时计算较小段的中位数。
2、中值滤波实验
1)通过中值滤波进行降噪
代码
fs = 200;%频率
t = 0:1/fs:2;
x = sin(2*pi*t*5)+0.25*sin(2*pi*t*80);
y = medfilt1(x,3);
plot(t,x,'-','color','r')
hold on;
plot(t,y,'-^','color','g')
legend('原始信号','滤波后信号')视图效果
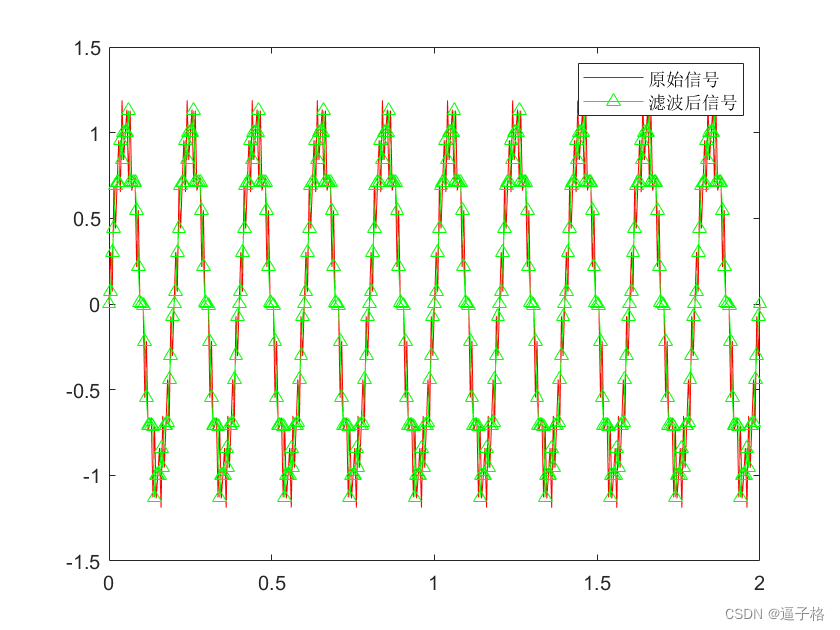
2)带有尖峰和丢失样本的多通道信号中值滤波
说明:
生成一个由不同频率正弦波组成的双通道信号。在随机位置加入尖峰。在随机位置用NaN添加缺失样本。重置随机数生成器设置加入噪声位置。
多通道信号生成代码
rng('default')
n = 59;
x = sin(pi./[10 20]'*(1:n)+pi/6)';
spk = randi(100,9,1);
x(spk) = x(spk)*2;
x(randi(100,6,1)) = NaN;
plot(x,'color','r')
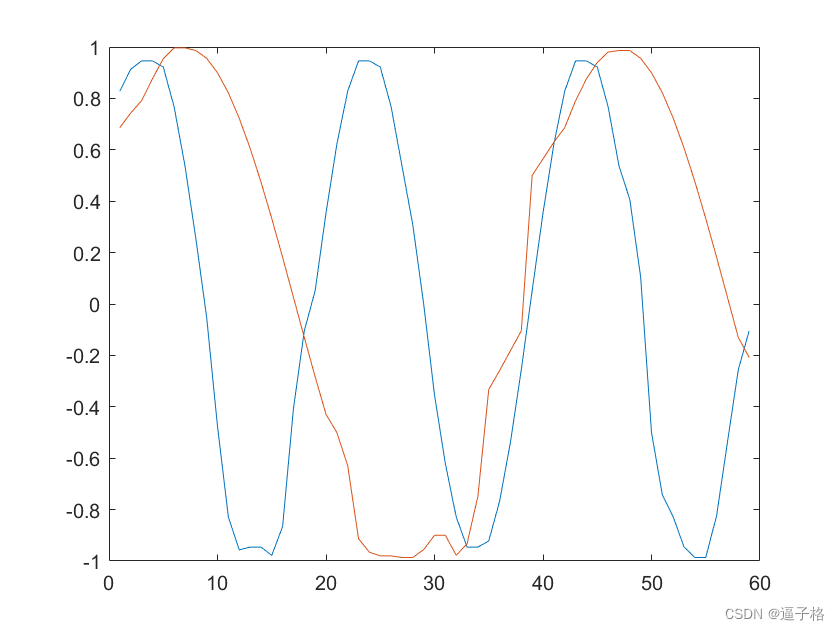
legend('信号1','信号2')试图效果
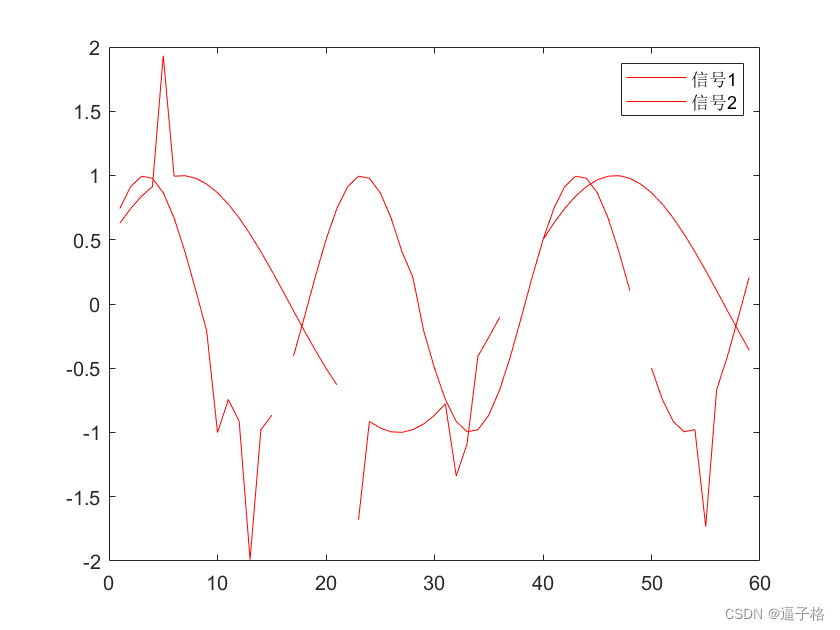
中值滤波效果对比
代码
rng('default')
n = 59;
x = sin(pi./[10 20]'*(1:n)+pi/6)';
spk = randi(100,9,1);
x(spk) = x(spk)*2;
x(randi(100,6,1)) = NaN;
plot(x,'color','r')
legend('信号1','信号2')
hold on;
y = medfilt1(x,8);
plot(y,'color','g')
legend('信号1中值滤波','信号2中值滤波')试图效果
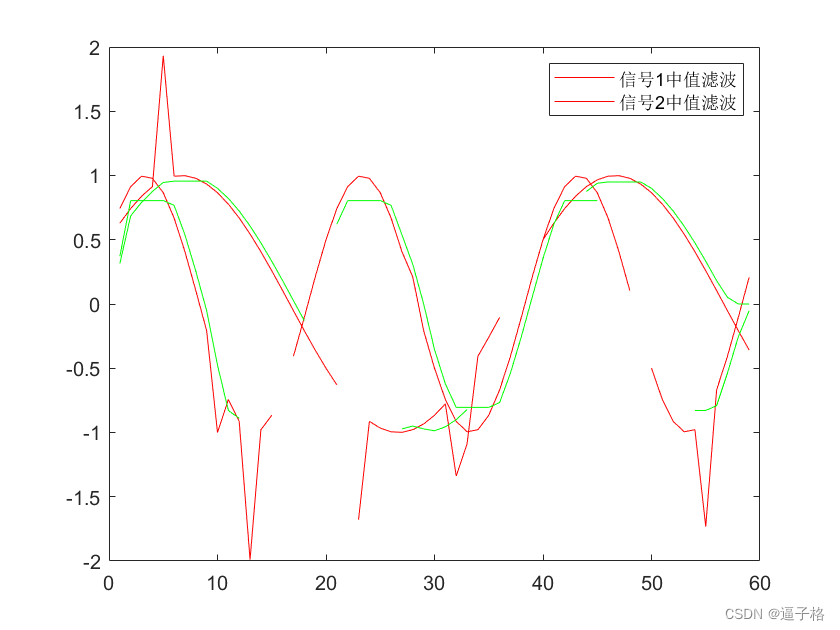
信号缺失部分处理(NaN)
代码
y = medfilt1(x,4,'omitnan');
plot(y)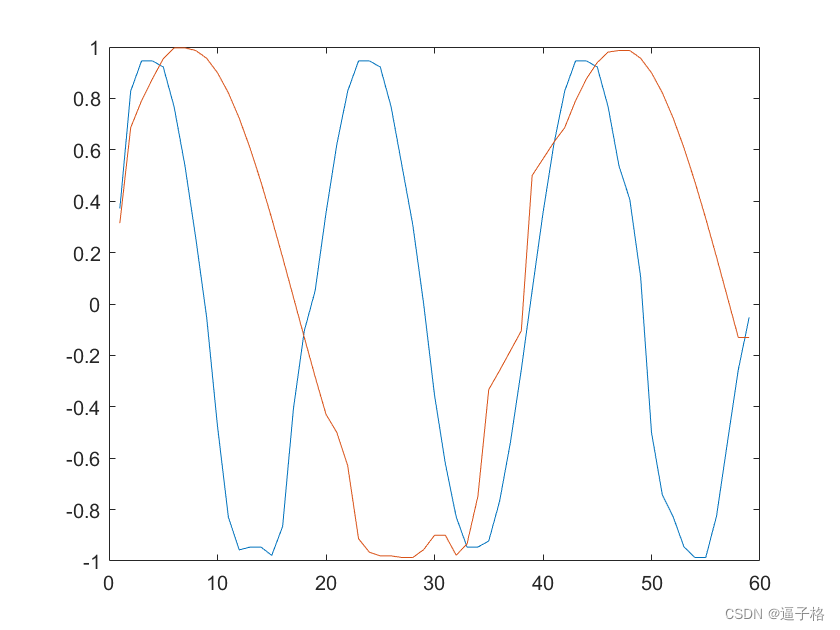
边缘滤波
代码
y = medfilt1(x,4,'omitnan','truncate');
plot(y)视图效果
3、 萨维茨基-戈雷滤波滤波器:sgolayfilt()
说明:萨维茨基-戈雷滤波
语法
语法1:y = sgolayfilt(x,order,framelen) 对向量 x 中的数据应用多项式阶数为 order、帧长度为
framelen 的萨维茨基-戈雷有限冲激响应 (FIR) 平滑滤波器。
语法2:y = sgolayfilt(x,order,framelen,weights) 指定在最小二乘最小化过程中要使用的加权向量。
语法3:y = sgolayfilt(x,order,framelen,weights,dim) 指定滤波器沿其运算的维度。
参数
x:输入信号 order:多项式阶数 framelen:帧长度 weights:加权数组 dim:要沿其滤波的维度
1)稳态和瞬变萨维茨基-戈雷滤波器
萨维茨基-戈雷滤波器滤波代码
order = 4;%参数设置 可以根据需求设置
framelen = 13;
l = 40;
x = randn(l,1);
sgf = sgolayfilt(x,order,framelen);
plot(x,':')
hold on
plot(sgf,'.-')
legend('原信号','戈雷滤波信号')
hold on视图效果
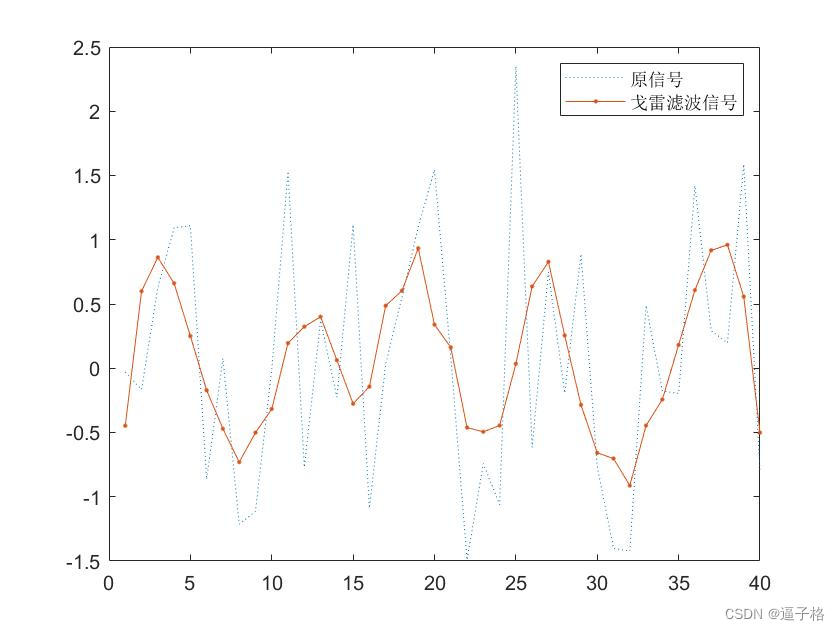
2) 稳态萨维茨基-戈雷滤波器滤波代码
order = 4;%参数设置 可以根据需求设置
framelen = 13;
l = 40;
x = randn(l,1);
sgf = sgolayfilt(x,order,framelen);
plot(x,':')
hold on
plot(sgf,'.-')
% legend('原信号','戈雷滤波信号')
hold on
m = (framelen-1)/2;
B = sgolay(order,framelen);
steady = conv(x,B(m+1,:),'same');%原信号与过滤信号卷积滤波 得到稳态部分
plot(steady)
legend('原信号','戈雷滤波信号','稳态部分')
视图效果
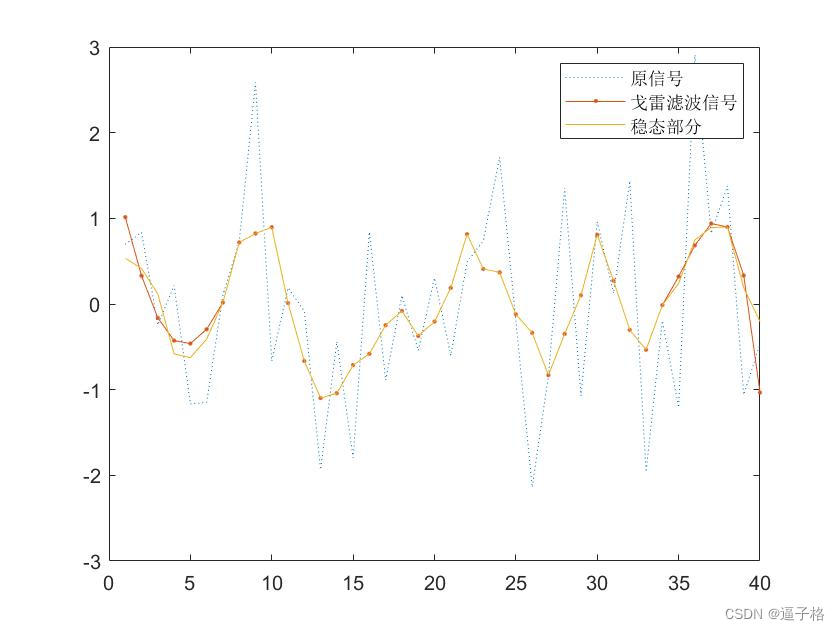
3)启动瞬态和终止瞬态代码
order = 4;%参数设置 可以根据需求设置
framelen = 13;
l = 40;
x = randn(l,1);
sgf = sgolayfilt(x,order,framelen);
plot(x,':')
hold on
plot(sgf,'.-')
% legend('原信号','戈雷滤波信号')
hold on
m = (framelen-1)/2;
B = sgolay(order,framelen);
steady = conv(x,B(m+1,:),'same');%原信号与过滤信号卷积滤波 得到稳态部分
plot(steady)
legend('原信号','戈雷滤波信号','稳态部分')ybeg = B(1:m,:)*x(1:framelen);%启动瞬态
yend = B(framelen-m+1:framelen,:)*x(l-framelen+1:l);%终止瞬态
cmplt = steady;
cmplt(1:m) = ybeg;
cmplt(l-m+1:l) = yend;plot(cmplt)
legend('原信号','戈雷滤波信号','稳态部分','完整信号')视图效果

相关文章:

19、matlab信号预处理中的中值滤波(medfilt1()函数)和萨维茨基-戈雷滤波滤(sgolayfilt()函数)
1、中值滤波:medfilt1()函数 说明:一维中值滤波 1)语法 语法1:y medfilt1(x) 将输入向量x应用3阶一维中值滤波器。 语法2:y medfilt1(x,n) 将一个n阶一维中值滤波器应用于x。 语法3:y medfilt1(x,n…...
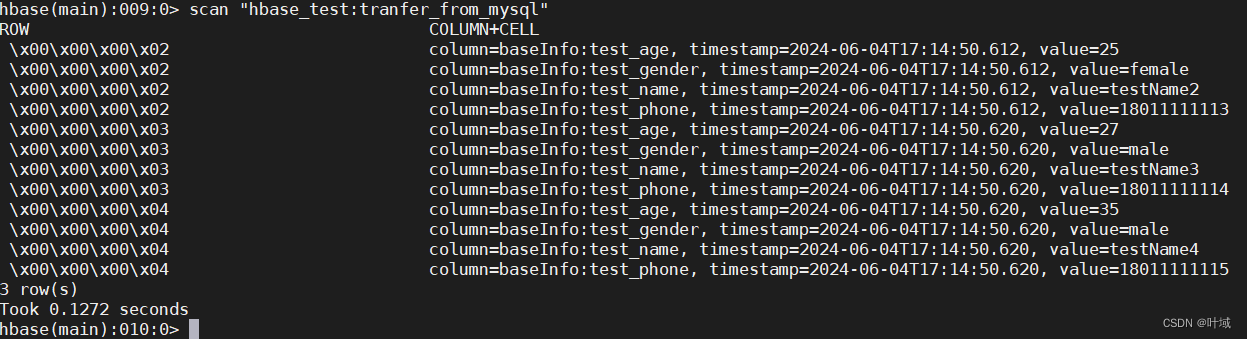
Scala 练习一 将Mysql表数据导入HBase
Scala 练习一 将Mysql表数据导入HBase 续第一篇:Java代码将Mysql表数据导入HBase表 源码仓库地址:https://gitee.com/leaf-domain/data-to-hbase 一、整体介绍二、依赖三、测试结果四、源码 一、整体介绍 HBase特质 连接HBase, 创建HBase执行对象 初始化…...

前端工程化:基于Vue.js 3.0的设计与实践
这里写目录标题 《前端工程化:基于Vue.js 3.0的设计与实践》书籍引言本书概述主要内容作者简介为什么选择这本书?结语 《前端工程化:基于Vue.js 3.0的设计与实践》书籍 够买连接—>https://item.jd.com/13952512.html 引言 在前端技术日…...
Linux☞进程控制
在终端执行命令时,Linux会建立进程,程序执行完,进程会被终止;Linux是一个多任务的OS,允许多个进程并发运行; Linxu中启动进程的两种途径: ①手动启动(前台进程(命令gedit)...后台进程(命令‘&’)) ②…...

mybatis离谱bug乱转类型
字符串传入的参数被转成了int: Param("online") String online<if test"online 0">and (heart_time is null or heart_time <![CDATA[ < ]]> UNIX_TIMESTAMP(SUBDATE(now(),INTERVAL 8 MINUTE)) )</if><if test"…...

视频监控管理平台LntonCVS视频汇聚平台充电桩视频监控应用方案
随着新能源汽车的广泛使用,公众对充电设施的安全性和可靠性日益重视。为了提高充电桩的安全管理和站点运营效率,LntonCVS公司推出了一套全面的新能源汽车充电桩视频监控与管理解决方案。 该方案通过安装高分辨率摄像头,对充电桩及其周边区域进…...

VS环境Python:深度探索与实用指南
VS环境Python:深度探索与实用指南 在编程领域,VS环境(Visual Studio环境)与Python的结合,为开发者们提供了一种强大而灵活的开发体验。这种结合不仅提升了开发效率,还增强了代码的可读性和可维护性。然而&…...
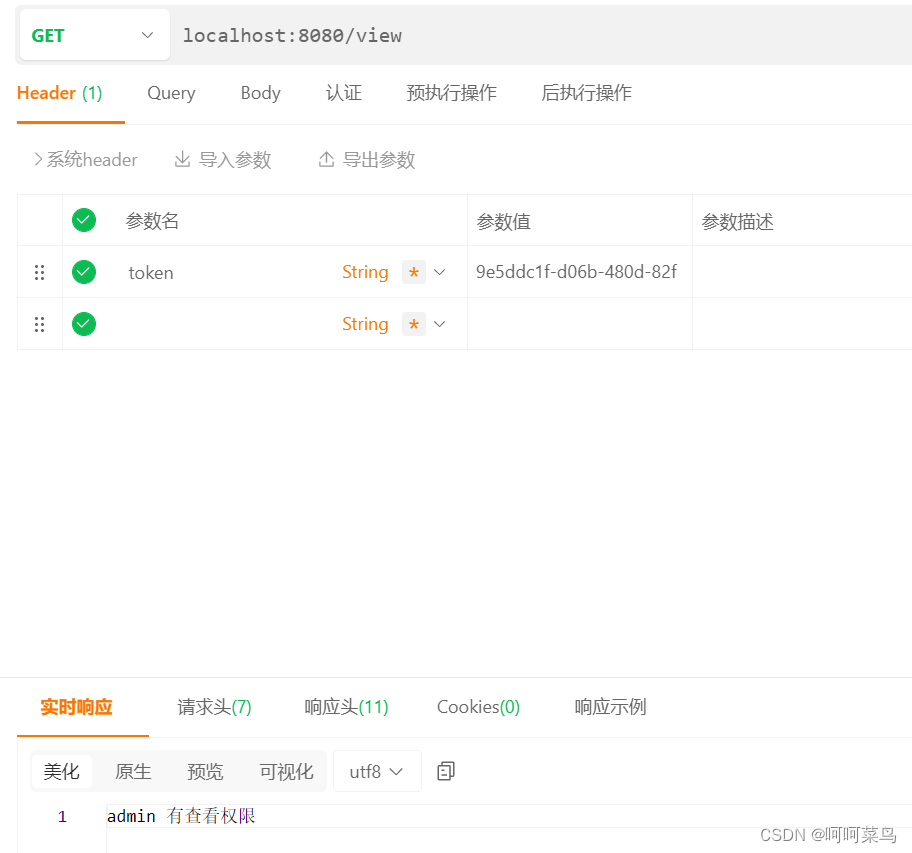
SpringBoot整合SpringSecurit(二)通过token进行访问
在文章:SpringBoot整合SpringSecurit(一)实现ajax的登录、退出、权限校验-CSDN博客 里面,使用的session的方式进行保存用户信息的,这一篇文章就是使用token的方式。 在其上进行的改造,可以先看SpringBoot…...

【算法训练 day50 打家劫舍、打家劫舍Ⅱ、打家劫舍Ⅲ】
目录 一、打家劫舍-LeetCode 198思路 二、打家劫舍Ⅱ-LeetCode 213思路 三.打家劫舍Ⅲ-LeeCode 337思路 一、打家劫舍-LeetCode 198 Leecode链接: leetcode 198 思路 dp数组含义为:当前数组范围下能偷到的最多的钱。递推公式为:dp[j] max(dp[j-2]nums[j],dp[j-1…...

YOLOv8改进 | 卷积模块 | 在主干网络中添加/替换蛇形卷积Dynamic Snake Convolution
💡💡💡本专栏所有程序均经过测试,可成功执行💡💡💡 蛇形动态卷积是一种新型的卷积操作,旨在提高对细长和弯曲的管状结构的特征提取能力。它通过自适应地调整卷积核的权重࿰…...
)
深入解析力扣183题:从不订购的客户(LEFT JOIN与子查询方法详解)
关注微信公众号 数据分析螺丝钉 免费领取价值万元的python/java/商业分析/数据结构与算法学习资料 在本篇文章中,我们将详细解读力扣第183题“从不订购的客户”。通过学习本篇文章,读者将掌握如何使用SQL语句来解决这一问题,并了解相关的复杂…...

牛客NC32 求平方根【简单 二分 Java/Go/C++】
题目 题目链接: https://www.nowcoder.com/practice/09fbfb16140b40499951f55113f2166c 思路 Java代码 import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** para…...

王道408数据结构CH3_栈、队列
概述 3.栈、队列和数组 3.1 栈 3.1.1 基本操作 3.1.2 顺序栈 #define Maxsize 50typedef struct{ElemType data[Maxsize];int top; }SqStack;3.1.3 链式栈 typedef struct LinkNode{ElemType data;struct LinkNode *next; }*LiStack;3.2 队列 3.2.1 基本操作 3.2.2 顺序存储…...

Angular 由一个bug说起之六:字体预加载
浏览器在加载一个页面时,会解析网页中的html和css,并开始加载字体文件。字体文件可以通过css中的font-face规则指定,并使用url()函数指定字体文件的路径。 比如下面这样: css font-face {font-family: MyFont;src: url(path/to/font.woff2…...

并查集进阶版
过关代码如下 #define _CRT_SECURE_NO_WARNINGS #include<bits/stdc.h> #include<unordered_set> using namespace std;int n, m; vector<int> edg[400005]; int a[400005], be[400005]; // a的作用就是存放要摧毁 int k; int fa[400005]; int daan[400005]…...
贪心(不相交的开区间、区间选点、带前导的拼接最小数问题)
目录 1.简单贪心 2.区间贪心 不相交的开区间 1.如何删除? 2.如何比较大小 区间选点问题 3.拼接最小数 1.简单贪心 比如:给你一堆数,你来构成最大的几位数 2.区间贪心 不相交的开区间 思路: 首先,如果有两个…...

[力扣题解] 617. 合并二叉树
题目:617. 合并二叉树 思路 递归法遍历,随便一种遍历方式都可以,以前序遍历为例; 代码 class Solution { public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if(root1 NULL){return root2;}if(root2 NULL){r…...
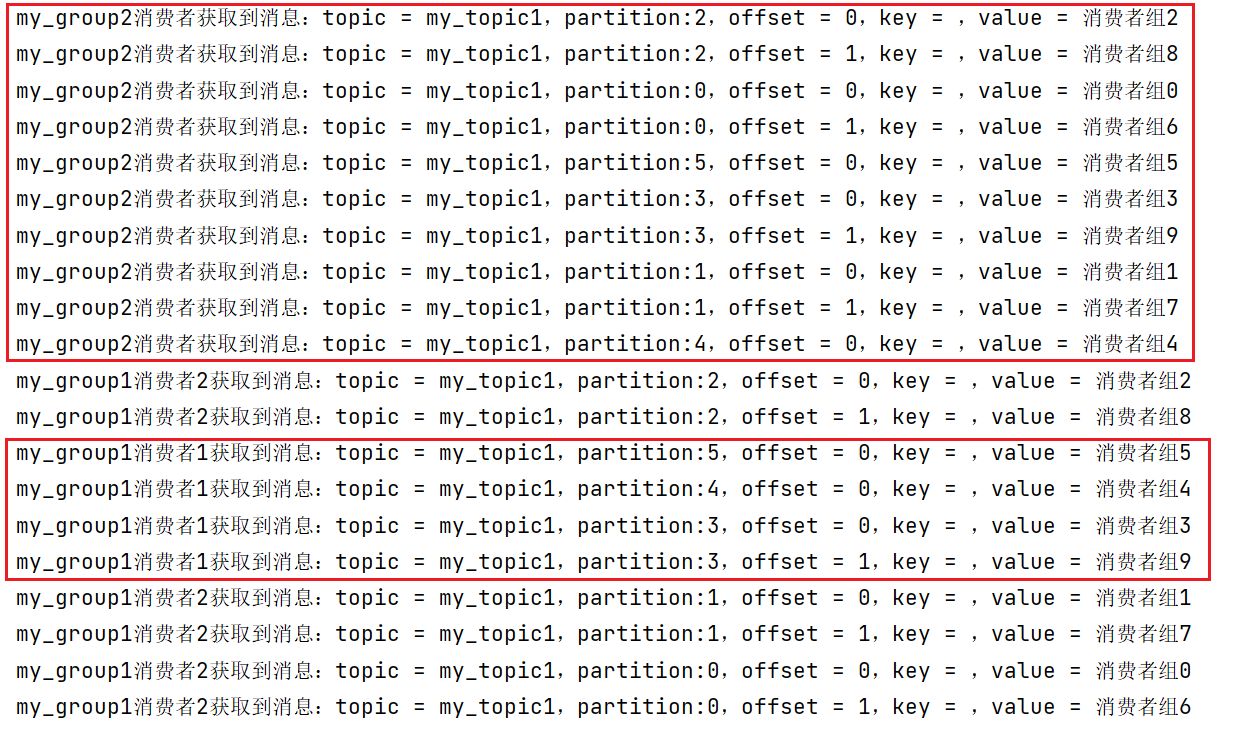
kafka-消费者组(SpringBoot整合Kafka)
文章目录 1、消费者组1.1、使用 efak 创建 主题 my_topic1 并建立6个分区并给每个分区建立3个副本1.2、创建生产者发送消息1.3、application.yml配置1.4、创建消费者监听器1.5、创建SpringBoot启动类1.6、屏蔽 kafka debug 日志 logback.xml1.7、引入spring-kafka依赖1.8、消费…...

Redisson知识
使用Redission获取锁 RLock lock redisson.getLock("my-lock"); 一、Redisson使用不指定锁过期时间的方式加锁: lock.lock(); 特点: 1.使用Redisson加的锁,具有自动续期机制,如果业务运行时间较长,运行…...

0103__【C/C++ 单线程性能分析工具 Gprof】 GNU的C/C++ 性能分析工具 Gprof 使用全面指南
【C/C 单线程性能分析工具 Gprof】 GNU的C/C 性能分析工具 Gprof 使用全面指南-CSDN博客...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
