动态规划入门经典问题讲解
最近开始接触动态规划问题,以下浅谈(或回顾)一下这些问题的求解过程。
解题思路
对于动态规划问题,由于最终问题的求解需要以同类子问题作为基础,故需要定义一个dp数组(一维或二维)来记录问题求解的各个状态(避免多次求算重复子问题);然后就是确认状态转移方程,也就是问题求解的递推公式;由于问题的最终状态需要从最初状态递推而来,故需初始化状态,即初始化dp数组。
步骤如下:
确定dp数组以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组
(上述步骤来自代码随想录)
爬楼梯问题
爬楼梯时每一次只能上1级或2级阶梯,问爬n级阶梯有多少种方法?
这是一个最简单的动态规划问题,以下是解题步骤:
定义数组int dp[1005],根据问题的问法,设dp[n]表示爬n级楼梯时的方法总数;
确认状态转移方程,我们直接考虑最后一次爬上n级楼梯的方法。显然,最后一次无非直接爬1级阶梯上到第n级,或者爬2级阶梯上到了第n级。由于前者是发生在已爬n-1级阶梯的基础上,而后者发生在已爬n-2级阶梯的基础上。故爬n级阶梯的方法总数等于dp[n-1]+dp[n-2],即转台转移方程:dp[n] = dp[n-1]+dp[n-2];
确定初始状态,显然dp[n]需要从两个子状态推导而来,故问题的边界为,确认dp[1]与dp[2].易知,dp[1]=1,dp[2]=2;
确定遍历顺序,显然需要从dp[1]与dp[2]往后递推。
第一种情况

第二种情况

(图来自小灰漫画)
#include<iostream>
using namespace std;//dp[i]表示爬i级阶梯时所花费的步数
int dp[1005];
int main() {int n;cin >> n;//初始化dp[1] = 1;dp[2] = 2;//递推公式为:dp[i] = dp[i-1]+dp[i-2] (i>=3)for (int i = 3;i <= n;i++) {dp[i] = dp[i - 1] + dp[i - 2];}cout << dp[n] << endl;return 0;
}求最大子段
问题描述:给定一个数字序列,称由连续元素组成的序列为该数字序列的子段,问子段元素之和的最大值为何?
由于每一个子段必有一个前缀与后缀,最大子段必有一个前缀或者后缀,我们干脆定义dp[i]表示以序列中第i个元素为后缀的最大子段;定义int a[1005]存储数字序列的各个元素,a[i]表示序列中的第i个元素。解题步骤如下:
定义int dp[1005],dp[i]表示以序列中第i个元素为后缀的最大子段;
确认状态转移方程,每一个元素可以单独作为一个子段,因此对于dp[i]而言,其最大子串无非两种情况:第一,若dp[i-1]>0,那么a[i]单独作为子段,其必定小于第i元素与以序列中第i-1个元素为后缀的最大子段拼接所得到得新子段,此时dp[i] = dp[i-1]+a[i];若dp[i-1]<=0,那么a[i]单独作为子段会使dp[i]更大,故dp[i]=a[i]。即转移方程为:dp[i]=max(dp[i-1]+a[i],a[i]);
确认初始状态,显然获取dp[i]需要得知dp[i-1],即dp[1]=a[1]
确定遍历顺序,显然从左往右扫描即可。
#include<iostream>
using namespace std;
const int maxn = 1005;
int a[maxn];
int dp[maxn];int main() {int n;cin >> n;for (int i = 1;i <= n;i++) {cin >> a[i];}dp[1] = a[1];for (int i = 2;i <= n;i++) {dp[i] = max(dp[i - 1] + a[i], dp[i]);}int max = dp[1];for (int i = 2;i <= n;i++) {if (max < dp[i]) {max = dp[i];}}cout << max << endl;return 0;
}求最长上升子序列
问题描述:给定一个数字序列,取其中的部分元素(元素无需连续),要求元素按升序排列,问上升子序列的最大长度,也就是该子序列里面元素的最大个数。
依旧定义int dp[1005],其中dp[i]表示以序列中第i个元素为结尾的最长上升子序列。对于dp[i]最长上升子序列与后面元素有关,若a[i]>a[i-1]那么必定有dp[i]=dp[i-1]+1,可在a[i]后面的元素中,dp[i-1]并不一定就是最大的,依旧需要遍历dp[1]~dp[i-1]中,满足a[j]<a[i]且a[j]最大的那个上升子序列,从而接到a[i]后面,解题思路如下:
定义int dp[1005],dp[i]表示以序列中第i个元素为结尾的最长上升子序列;
确认递推公式,dp[i] = max(dp[i-1],dp[i-2],..........,dp[1])+1;
确认初始化状态,显然每一个元素的都至少可以单独构成一个长度为1的最长上升子序列,从而设置dp[0]=0,a[0]=-inf (inf表示无穷大),保证序列中每一个元素都至少能大于a[0];
确认遍历顺序,依旧是从左往右扫描。
#include<iostream>
using namespace std;const int maxn = 1005;
int a[maxn];
int dp[maxn];
const int inf = 0xffffff;//求最长子序列,假设dp[i]表示以第i元素为结尾的最长上升子序列int main(){int n;cin >> n;a[0] = -inf;for (int i = 1;i <= n;i++) {cin >> a[i];}int ans = 0;for (int i = 1;i <= n;i++) {for (int j = 0;j < i;j++) {if (a[i] > a[j]) {dp[i] = max(dp[i], dp[j] + 1);}}ans = max(ans, dp[i]);}cout << ans << endl;return 0;
}求最大公共子串
问题描述:给定两个字符串a,b,求a与b中公共部分的元素个数.例如:a="abfed",b="bfd",那么最大公共子串ps = "bfd",其元素个数为3.
此时假定一个二维数组int dp[1005][1005],那么dp[i][j]表示a前i个字符构成的子串与b前j个字符构成的子串的最大公共子串。那么此时若a[i-1]==b[j-1],说明字符串a的第i个字符与字符串b的第j个字符相等,那么此时dp[i][j]=dp[i-1][j-1]+1;若a[i-1]!=b[j-1],dp[i][j]=max(dp[i-1][j],dp[i][j]),因为父串a与其他串b的最大子串一定大于或等于该父串a的子串与其他串b的最大子串.
解题思路:
定义int dp[1005][1005],dp[i][j]表示a前i个字符构成的子串与b前j个字符构成的子串的最大公共子串
确认递推公式,若a[i-1]==b[j-1],则dp[i][j]=dp[i-1][j-1]+1;否则,dp[i][j]=max(dp[i-1][j],dp[i][j]).
确认初始化状态,只需要初始化dp[0][0]=0即可。
确认遍历顺序,依旧是从左往右,从上往下扫描。
#include<iostream>
#include<string>
#include<cstdio>using namespace std;
int dp[105][105];
int main() {string a, b;cin >> a >> b;int lena = a.length();int lenb = b.length();memset(dp, 0, sizeof(dp));for (int i = 1;i <= lena;i++) {for (int j = 1;j <= lenb;j++) {if (a[i - 1] == b[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;}else {dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);}}}cout << dp[lena][lenb] << endl;return 0;
}求编辑距离
问题描述:给定一个字符串S与一个模板字符串T,可以对S进行插、替、删三种操作,问S经过上述操作变为T的最少次数,即为最小编辑距离。
依旧设int dp[1005][1005],其中dp[i][j]表示S的前i个字符与T的前j个字符的最小编辑距离。
解题思路:
定义int dp[1005][1005],dp[i][j]表示S的前i个字符与T的前j个字符的最小编辑距离;
确认递推公式,若a[i-1]==b[j-1],则dp[i][j]=dp[i-1][j-1];否则,在dp[i-1][j-1]、dp[i][j-1]、dp[i-1][j]中,若dp[i-1][j-1]最小说明需要将a[i-1]替换为b[j-1];若dp[i][j-1]最小,需要在S的前i个字符后面添加一个b[j-1];若dp[i-1][j]最小,需要删除a[i-1]。即dp[i][j]=min(dp[i][j-1],dp[i-1][j],dp[i-1][j-1])+1;
确认初始化状态,需要依次初始化dp[0][0]~dp[0][S.length()]以及dp[T.length()][0];
确认遍历顺序,依旧是从左往右,从上往下扫描。
#include<iostream>
#include<string>
using namespace std;int dp[105][105];//dp[i][j]表示S前i个字符与T前j个字符编辑时的最小距离//求编辑距离
int func(string S,string T) {int lenS;int lenT;lenS = S.length();lenT = T.length();dp[0][0] = 0;for (int i = 1;i <= lenS;i++) {dp[i][0] = i;}for (int j = 1;j <= lenT;j++) {dp[0][j] = j;}for (int i = 1;i <= lenS;i++) {for (int j = 1;j <= lenT;j++) {if (S[i - 1] == T[j - 1]) {dp[i][j] = dp[i - 1][j - 1];}else {dp[i][j] = min(min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i][j - 1]) + 1;}}}return dp[lenS][lenT];
}int main() {string S, T;cin >> S >> T;cout << func(S, T) << endl;return 0;
}相关文章:

动态规划入门经典问题讲解
最近开始接触动态规划问题,以下浅谈(或回顾)一下这些问题的求解过程。解题思路对于动态规划问题,由于最终问题的求解需要以同类子问题作为基础,故需要定义一个dp数组(一维或二维)来记录问题求解…...

快速入门深度学习1(用时1h)
速通《动手学深度学习》1写在最前面0.内容与结构1.深度学习简介1.1 问题引入1.2 思路:逆向思考1.3 跳过1.4 特点1.5 小结2.预备知识(MXNet版本,学错了。。。。)2.1 获取和运行本书的代码2.2 数据操作2.2.1 略过2.2.2 小结2.3 自动…...
PaddleOCR关键信息抽取(KIE)的训练(SER训练和RE训练)错误汇总
1.SER训练报错: SystemError: (Fatal) Blocking queue is killed because the data reader raises an exception 1.1.问题描述 在执行训练任务的时候报错 单卡训练 python3 tools/train.py -c train_data/my_data/ser_vi_layoutxlm_xfund_zh.yml错误信息如下: T…...

信息收集之搜索引擎
Google Hacking 也可以用百度,不过谷歌的搜索引擎更强大 site 功能:搜索指定域名的网页内容,可以用来搜索子域名、跟此域名相关的内容 示例: site:zhihu.com 搜索跟zhihu.com相关的网页“web安全” site:zhihu.com 搜索zhihu…...
布局类组件)
Flutter(四)布局类组件
目录布局类组件简介布局原理与约束线性布局(Row和Column)弹性布局流式布局(Wrap、Flow)层叠布局(Stack、Positioned)对齐与相对定位(Align)Align和Stack对比Center组件LayoutBuilder…...

【黑马】Java基础从入门到起飞目录合集
视频链接: Java入门到起飞(上部):BV17F411T7AoJava入门到起飞(下部):BV1yW4y1Y7Ms 学习时间: 2023/02/01 —— 2023/03/09断断续续的学习,历时大概37天,完结撒…...

PMP考前冲刺3.10 | 2023新征程,一举拿证
题目1-2:1.在最近的一次耗时四周的迭代中,赫克托尔所在的敏捷团队刚完成了10 个用户故事点的开发、测试和发布,那么团队的速度是?A. 10B. 4C. 5D.402.产品负责人奥佩,倾向于在短周期内看到工作产品的新版本,…...

JavaScript Math常用方法
math是JavaScript的一个内置对象,它提供了一些数学属性和方法,可以对数字进行计算(用于Number类型)。 math和其他全局对象不同,它不是一个构造器,math的所有方法和属性都是静态的,直接使用并传入…...

【C++】模板进阶
文章目录一、非类型模板参数1、非类型模板参数2、C11 中的 array 类二、模板的特化1、模板特化的概念2、函数模板特化3、类模板特化3.1 全特化3.2 偏特化三、模板的分离编译四、模板总结一、非类型模板参数 1、非类型模板参数 模板参数分为类型形参与非类型形参,类…...

三板斧解决leetcode的链表题
在《波奇学单链表》中我们提到单链表的两个特点单向性。头节点尾节点的特殊性导致分类讨论的情况。如何看单链表?让我们简化成下图cur表示当前节点,下图表示cur移动,圆圈表示值用哨兵卫节点(新的头节点)和把尾节点看成NULL来把头尾节点一般化…...
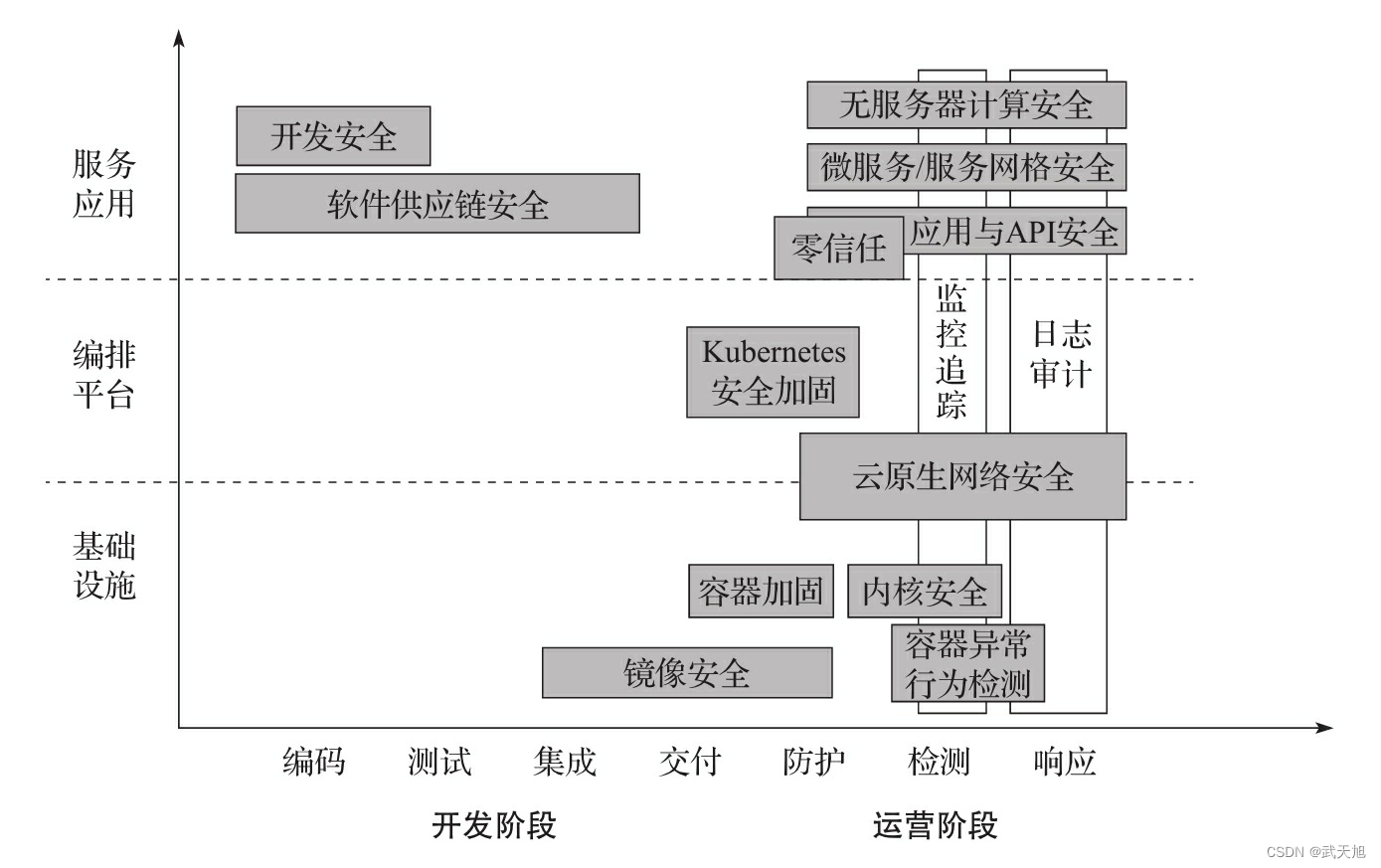
全生命周期的云原生安全框架
本博客地址:https://security.blog.csdn.net/article/details/129423036 一、全生命周期的云原生安全框架 如图所示: 二、框架说明 在上图中,我们从两个维度描述各个安全机制,横轴是开发和运营阶段,细分为编码、测试…...
【本地网站上线】ubuntu搭建web站点,并内网穿透发布公网访问
【本地网站上线】ubuntu搭建web站点,并内网穿透发布公网访问前言1. 本地环境服务搭建2. 局域网测试访问3. 内网穿透3.1 ubuntu本地安装cpolar3.2 创建隧道3.3 测试公网访问4. 配置固定二级子域名4.1 保留一个二级子域名4.2 配置二级子域名4.3 测试访问公网固定二级子…...
电脑怎么重装系统?教你轻松掌握这些方法
重新安装计算机系统有两种原因:一种是计算机系统可以正常使用,但是电脑比较卡,为了提高它的运行速度,所以想要通过重新安装系统来解决这个问题;另一种原因是计算机系统文件丢失,系统出现蓝屏,或者黑屏的情况…...
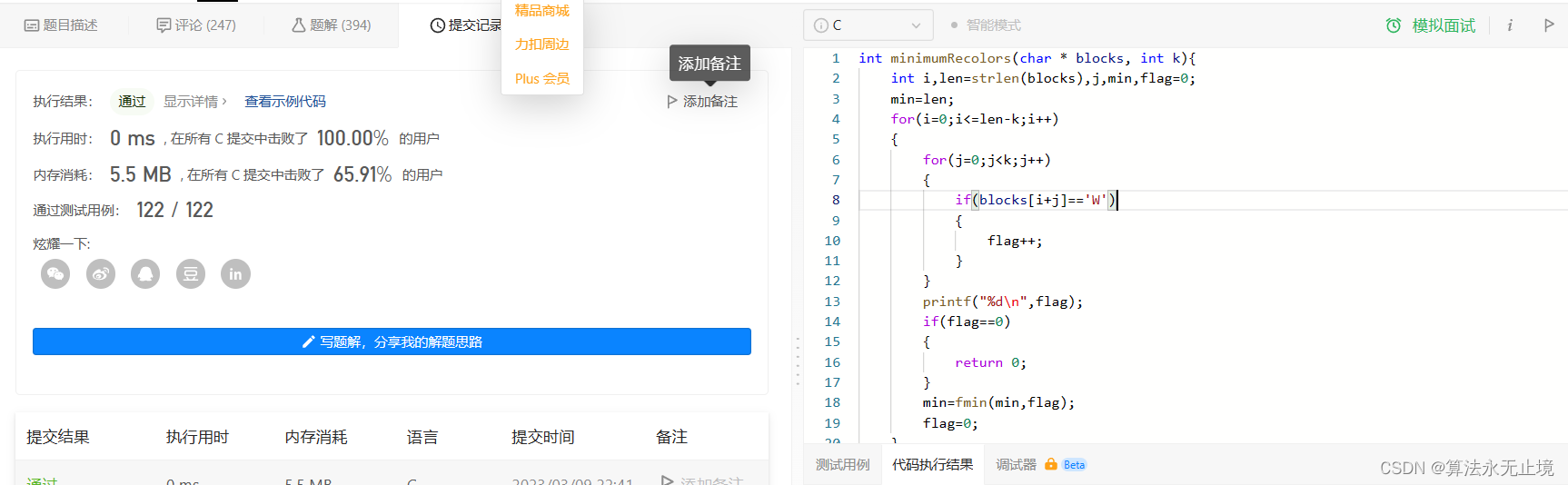
leetcode-每日一题-2379(简单,字符串)
久违的简单题......给你一个长度为 n 下标从 0 开始的字符串 blocks ,blocks[i] 要么是 W 要么是 B ,表示第 i 块的颜色。字符 W 和 B 分别表示白色和黑色。给你一个整数 k ,表示想要 连续 黑色块的数目。每一次操作中,你可以选择…...

SLF4J日志框架在项目中使用
介绍 SLF4J全称“Simple Logging Facade for Java”,作为各种日志框架的简单门面。例如: java.util.logging、logback 、 reload4j等。只需要切换日志框架的jar包依赖就可以切换日志框架。 SLF4J支持的日志框架包含如下: log4j:…...

Spark MLlib 模型训练
Spark MLlib 模型训练决策树随机森林GBDTSpark MLlib 开发框架下 : 监督学习 : 回归 (Regression) , 分类 (Classification) , 协同过滤 (Collaborative Filtering)非监督学习 : 聚类 (Clustering) 、频繁项集 (Frequency Patterns) 例子分类 : 算法分类 : 算法分类算法子分类…...

Python中变量的作用域精讲
文章目录前言一、局部变量二、全局变量前言 变量的作用域是指程序代码能够访问该变量的区域,如果超出该区域,再访问时就会出现错误。在程序中,一般会根据变量的 “有效范围” 将变量分为 “全局变量” 和 “局部变量”。 一、局部变量 局部变…...

数据仓库工程师的工作职责的相关介绍
1. BI 开发工程师的工作内容是什么? BI开发工程师(Business Intelligence Developer)是负责设计和开发企业级BI系统的专业人员。他们的主要工作是从多个数据源中提取、转换、加载和分析数据,以支持企业决策。以下是BI开发工程师的…...

ESP UART 介绍
1 UART 介绍 UART 是一种以字符为导向的通用数据链,可以实现设备间的通信。异步传输的意思是不需要在发送数据上添加时钟信息。这也要求发送端和接收端的速率、停止位、奇偶校验位等都要相同,通信才能成功。 1.1 UART 通信协议 一个典型的 UART 帧开始…...

第十三届蓝桥杯省赛Python大学B组复盘
目录 一、试题B:寻找整数 1、题目描述 2、我的想法 3、官方题解 4、另解 二、试题E:蜂巢 1、题目描述 2、我的想法 3、官方题解 三、试题F:消除游戏 1、题目描述 2、我的想法(AC掉58.3%,剩下全超时&#x…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...
