数据结构之排序算法
目录
1. 插入排序
1.1.1 直接插入排序代码实现
1.1.2 直接插入排序的特性总结
1.2.1 希尔排序的实现
1.2.2 希尔排序的特性总结
2. 选择排序
2.1.1 选择排序
2.1.2 选择排序特性
2.2.1 堆排序
2.2.2 堆排序特性
3. 交换排序
3.1.1 冒泡排序
3.1.2 冒泡排序的特性
3.2.1 快速排序
3.2.1.1 hoare版本
3.2.1.2 挖坑法
3.2.1.3 前后指针法
3.2.2.1 快排的递归实现及优化
3.2.2.2 快排的非递归实现
3.2.2 快速排序的特性
4. 归并排序
4.1 归并递归实现
4.2 归并非递归实现
5. 非比较排序
5.1 计数排序
5.2 基数排序
5.3 桶排序
6. 排序算法复杂度及稳定性
1. 插入排序
1.1.1 直接插入排序代码实现
插入排序动图如下:

思想就是把[0,end]区间变为有序让后把下一个数据进行插入下面是代码实现:
我们先写一趟排序
int end ;
int tem = a[end + 1];
while (end >= 0)
{if (tem < a[end]){a[end + 1] = a[end];end--;}else{break;}
}
a[end + 1] = tem;之后我们用一个for循环控制end的值就可以了
完整代码如下所示:
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tem = a[end + 1];while (end >= 0){if (tem < a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tem;}
}1.1.2 直接插入排序的特性总结
1.2.1 希尔排序的实现
void shellsort(int* a, int n)
{int gap = 3;for (int i = 0; i < n - gap; i += gap){int end = i;int key = a[end + gap];while (end >= 0){if (key < a[end]){a[end + gap] = a[end];end--;}else{break;}}a[end + gap] = key;}}下面我们控制组数每组的开头是不一样的最后控制gap只有gap为1时是最后一趟排序其余的都是预排序完整代码如下:
void shellsort(int* a, int n)
{int gap = n;while (gap>1){gap = gap / 3 + 1;for (int j = 0; j < gap; j++){for (int i = j; i < n - gap; i += gap){int end = i;int key = a[end + gap];while (end >= 0){if (key < a[end]){a[end + gap] = a[end];end-=gap;}else{break;}}a[end + gap] = key;}}}
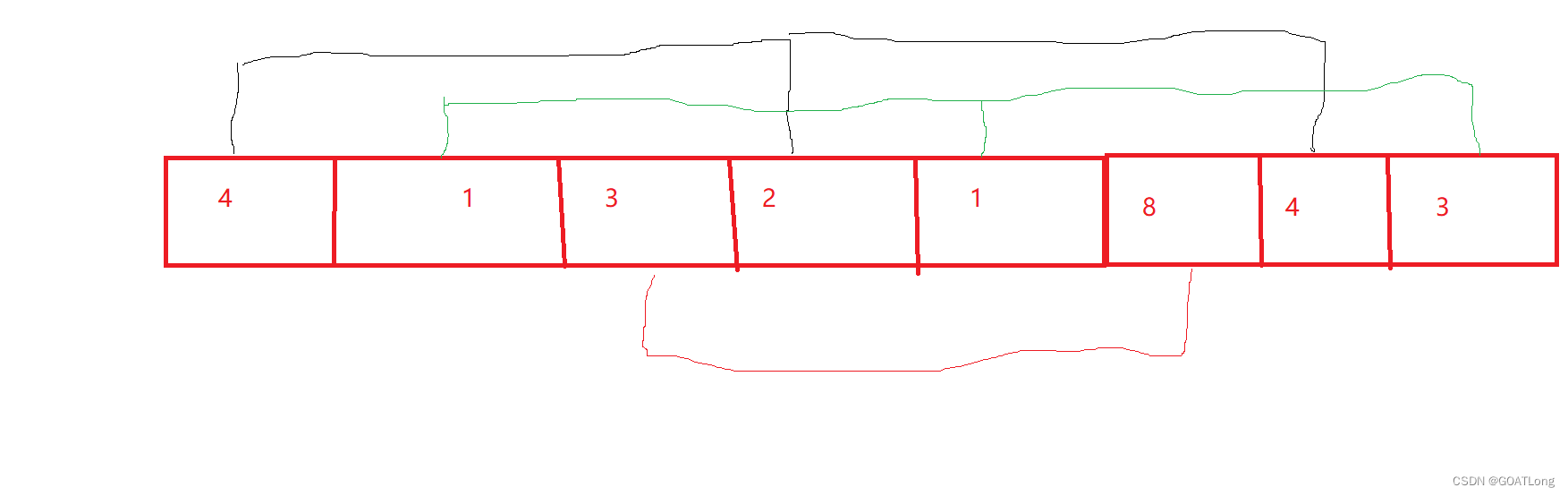
}下面是另一种写法两种写法的效率是一样的第二种写法就是进行一组两个数据的插入后直接进行下一组
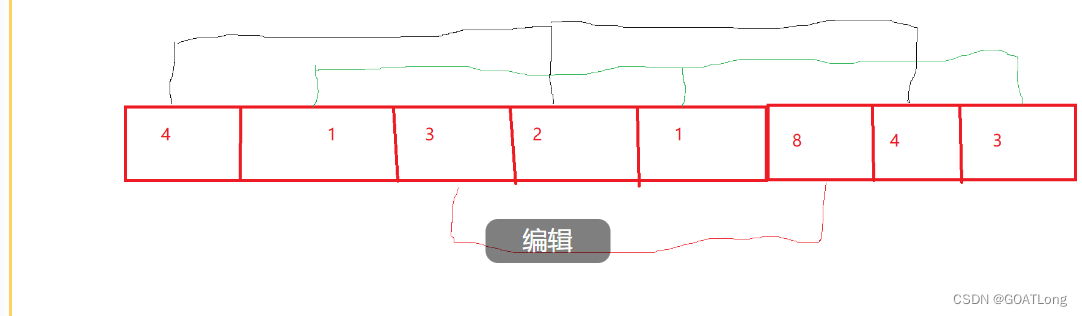
就是先4,2然后1,1然后3,8;第一种是一组全部弄完后再弄下一组两者的效率一样的
第二种代码如下:
void shellsort(int* a, int n)
{int gap = n;while (gap>1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int key = a[end + gap];while (end >= 0){if (key < a[end]){a[end + gap] = a[end];end-=gap;}else{break;}}a[end + gap] = key;}}
}1.2.2 希尔排序的特性总结
希尔排序的分析是一个复杂的问题,因为它的时间是所取"增量"序列的函数,这涉及
些数学上尚未解决的难题。因此,到目前为止尚未有人求得一种最好的增量序列,但大
量的研究已得出一些局部的结论。如有人指出,当增量序列为dIta[k]=25-6+1-1时,希
尔排序的时间复杂度为O(12312)其中t为排序趙数,1<k<t<log2(n+1)」。还有人在
大量的实验基础上推出
当刀在某个特定范围内,希尔排序所需的比较和移动次数为为
n1.3,当770时,可减少到7(10g27)201。增量序列可以有各种取法1,且需注意:应使增
量序列中的值没有除1之外的公因子,并且最后一个增量值必须等于1。
《数据结构-用面相对象方法与C++描述》---殷人昆
2. 选择排序
2.1.1 选择排序
思想就是便利找到一个最大一个最小最小放在起始位置最大放在最后的位置
代码实现:
void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;while (begin < end){int maxindex = begin;int minindex = begin;for (int i = begin + 1; i <= end; i++){if (a[i] > a[maxindex]){maxindex = i;}if (a[i] < a[minindex]){minindex = i;}}Swap(&a[begin], &a[minindex]);//这里我们要注意如果maxindex指向与begin相等时,换位之后maxindex要更新if (begin == maxindex)maxindex = minindex;Swap(&a[end], &a[maxindex]);begin++;end--;}
}2.1.2 选择排序特性
2.2.1 堆排序
堆排序就是先建堆然后按照堆的删除把堆顶数据放到数组最后让后end减减向下调整就行
代码实现如下:
void AddjustDown(int* a, int n, int parent)
{int child = 2 * parent + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}}
//堆排序
void HeapSort(int* a, int n)
{for (int i = (n - 2) / 2; i >= 0; i--){AddjustDown(a, n, i);}int end = n - 1;while (end >= 0){Swap(&a[0], &a[end]);AddjustDown(a, end, 0);end--;}
}2.2.2 堆排序特性
3. 交换排序
3.1.1 冒泡排序
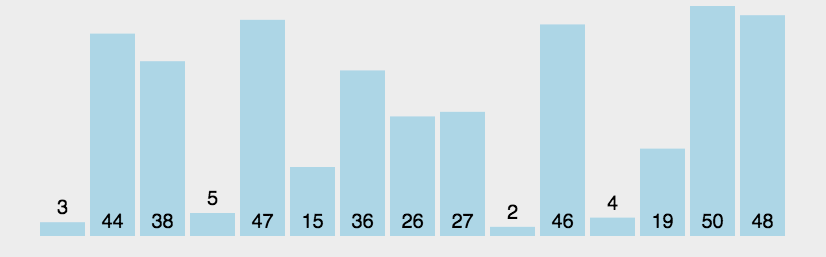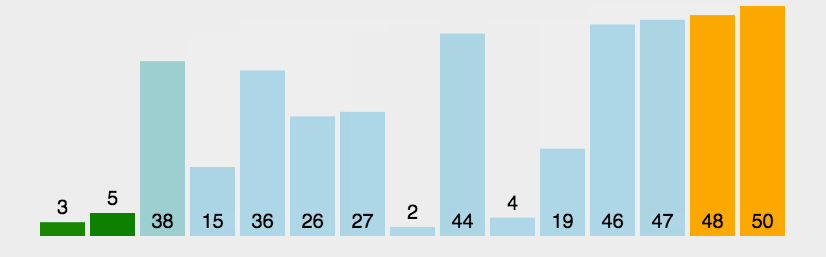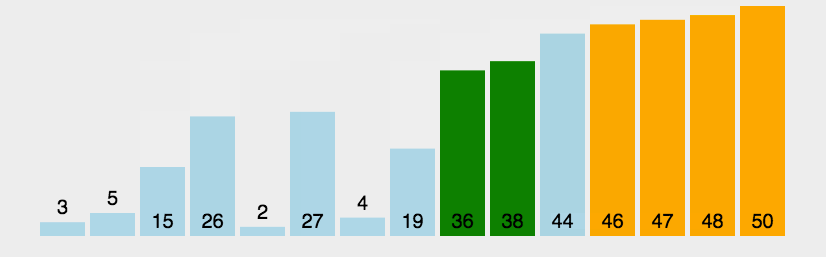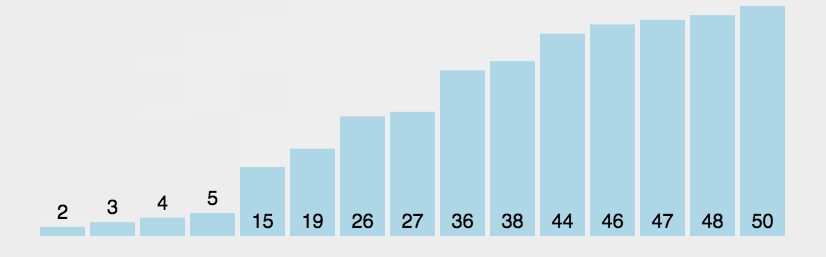
代码实现:
void BubbleSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int falg = 1;for (int j = 0; j < n - 1 - i ;j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);}falg = 0;}if (falg == 1){break;}}
}3.1.2 冒泡排序的特性
3.2.1 快速排序
3.2.1.1 hoare版本
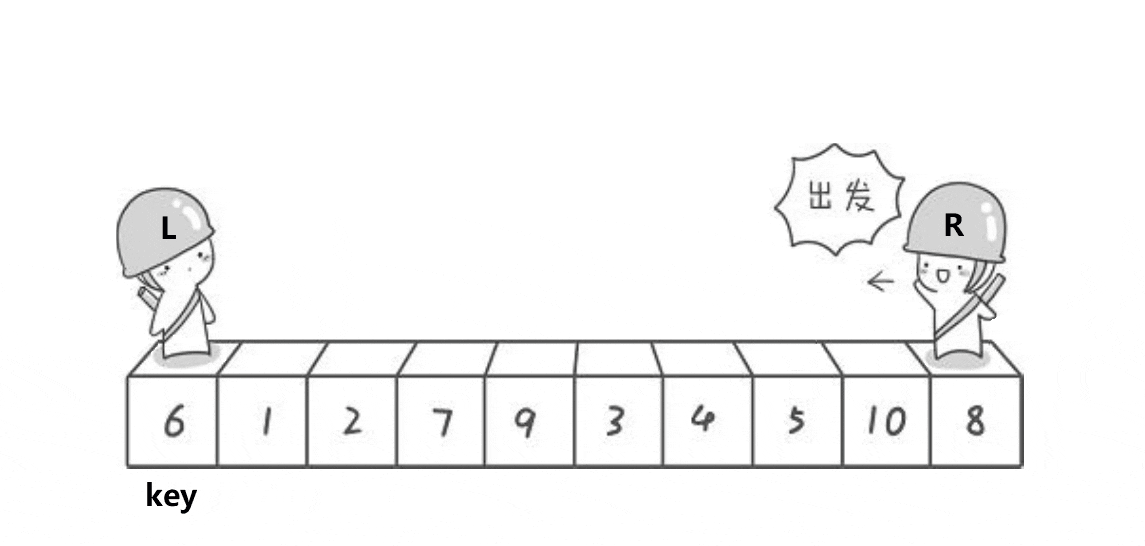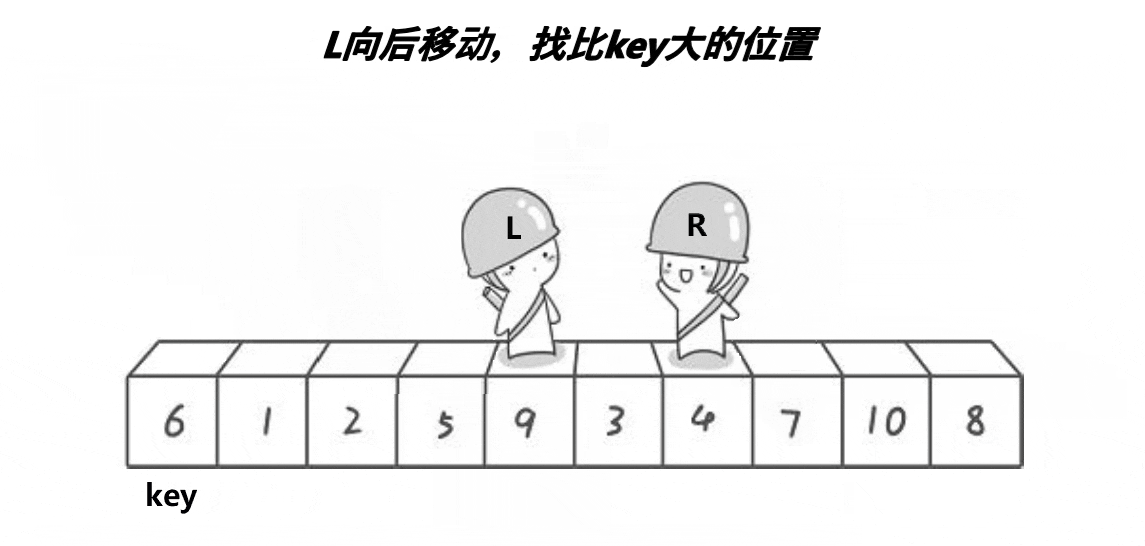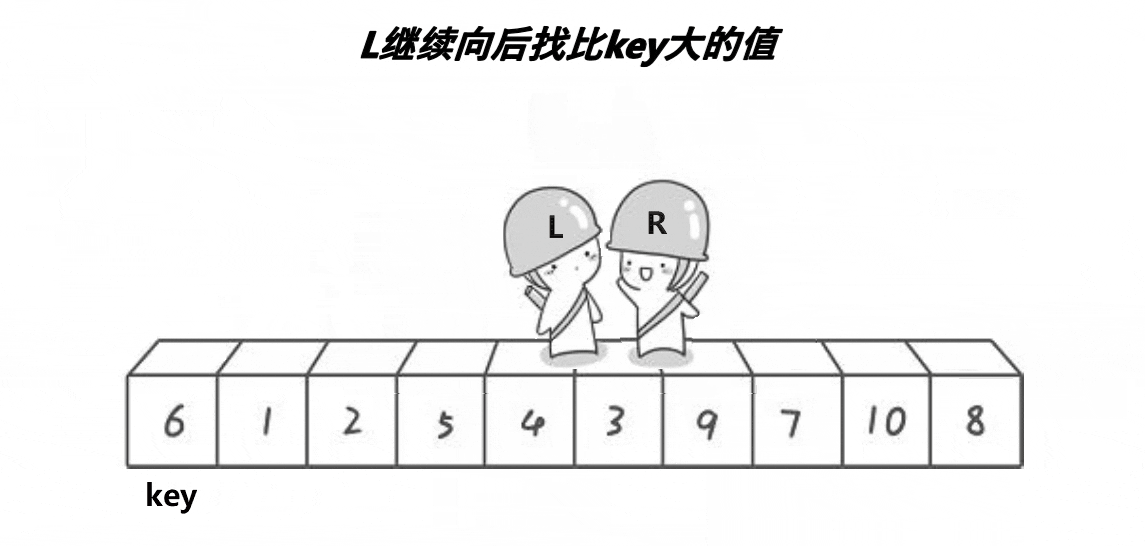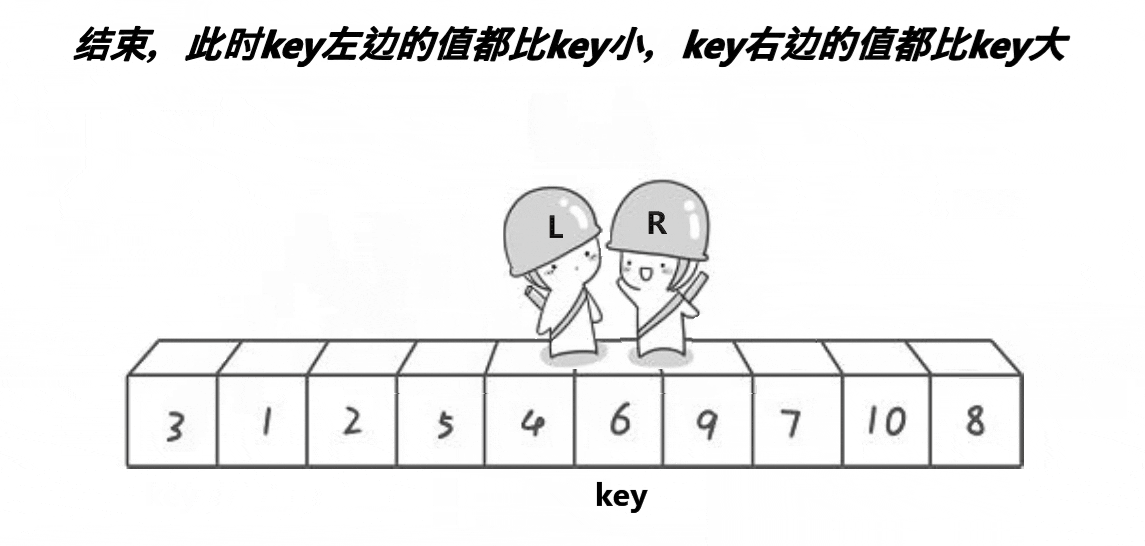
这里我们写的是单趟的逻辑
int PartSort1(int* a, int left, int right)
{int keyi = left;int begin = left;int end = right;while (begin < end){while (begin < end && a[end] >= a[keyi]){end--;}while (begin < end && a[begin] <= a[keyi]){begin++;}Swap(&a[end], &a[begin]);}Swap(&a[begin], &a[keyi]);return begin;
}3.2.1.2 挖坑法
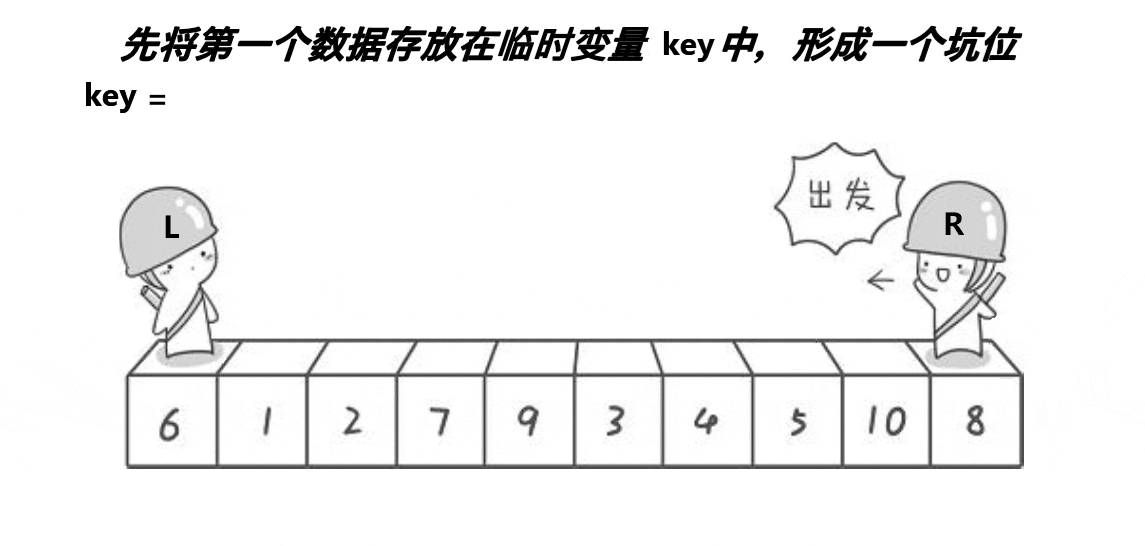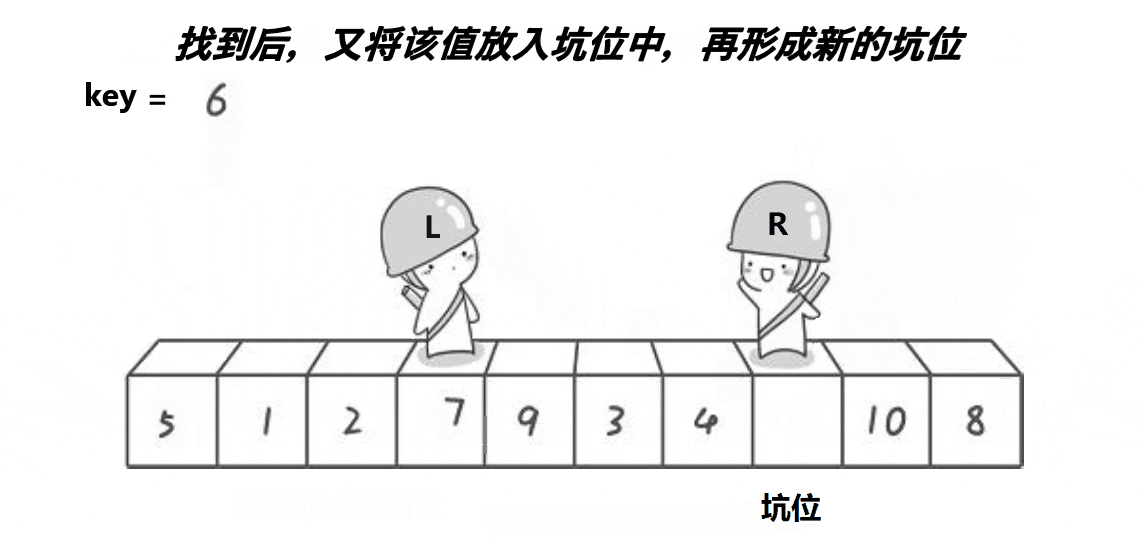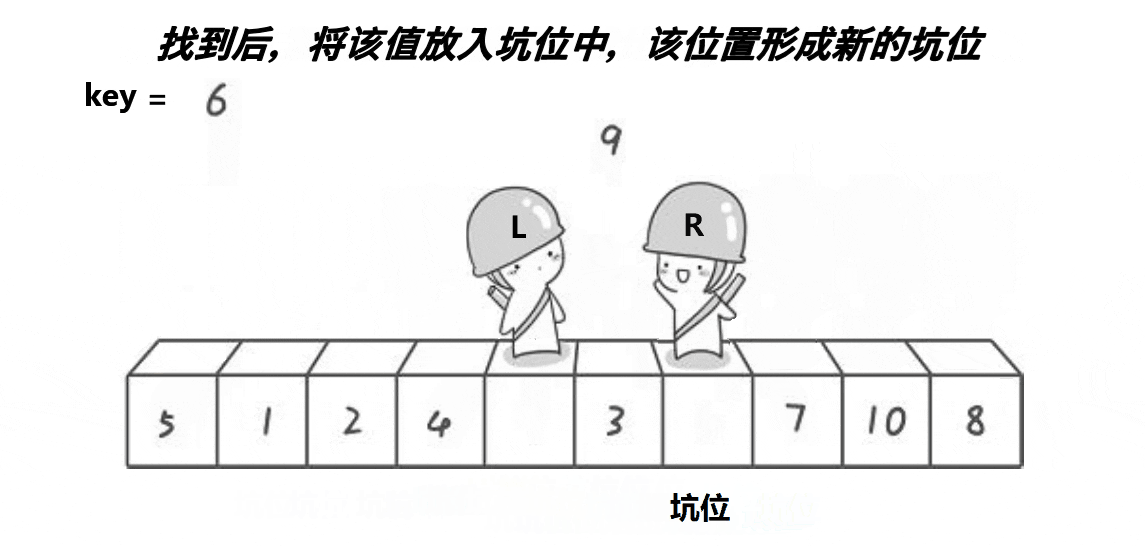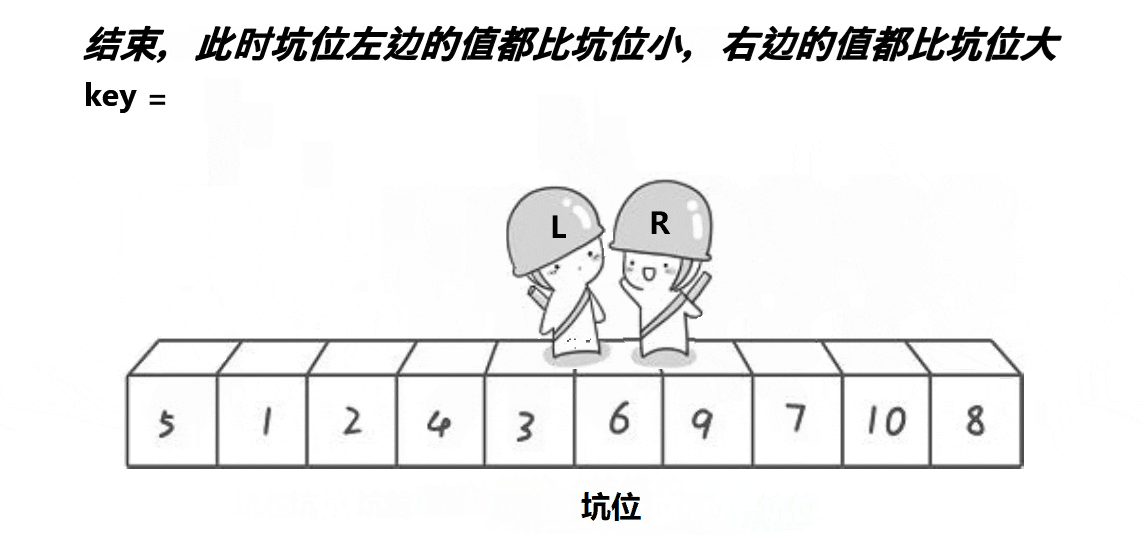
// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{int key = a[left];int keyi = left;int begin = left;int end = right;while (begin < end){while (begin < end && a[end] >= a[keyi]){end--;}a[keyi] = a[end];keyi = end;while (begin < end && a[begin] <= a[keyi]){begin++;}a[keyi] = a[begin];keyi = begin;}a[keyi] = key;return keyi;
}3.2.1.3 前后指针法

// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{int key = a[left];int prev = left;int cur = prev + 1;while (cur <= right){//这里当我们每次交换时prev先走是为了防止数组最左端的数据被覆盖if (a[cur] < key && ++prev!=cur)Swap(&a[cur], &a[prev]);cur++;}//这里注意要与数组的头一个序列的值交换Swap(&a[prev], &a[left]); return prev;
}3.2.2.1 快排的递归实现及优化
// 三数取中
int findmidi(int* a, int left, int right)
{int midi = (right - left) / 2 + left;if (a[left] >= a[midi]){if (a[midi] >=a[right]){return midi;}else if (a[right] >= a[midi]){if (a[left] <= a[right]){return left;}else{return right;}}}else//a[midi]>a[left]{if (a[right] >= a[midi]){return midi;}else if (a[right] <= a[midi]){if (a[right] >= a[left]){return right;}else{return left;}}}
}
void QuickSort(int* a, int left, int right)
{if (left >= right)return ;if (right - left + 1 <= 10){InsertSort(a + left, right - left + 1);return ;}else{int midi = findmidi(a, left, right);Swap(&a[midi], &a[left]);int mid = PartSort3(a, left, right);QuickSort(a, left, mid - 1);QuickSort(a, mid + 1, right);}
}其中的三数其中发是为了防止数据有序的情况下效率退化
而在数据足够少时不用再递归了减少了递归次数优化了效率
3.2.2.2 快排的非递归实现
//快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{Stack stack;StackInit(&stack);StackPush(&stack, right);StackPush(&stack, left);while (!StackEmpty(&stack)){int begin = StackTop(&stack);StackPop(&stack);int end = StackTop(&stack);StackPop(&stack);int mid = PartSort3(a, begin, end);if (mid + 1 < end){StackPush(&stack, end);StackPush(&stack, mid + 1);}if (begin < mid - 1){StackPush(&stack, mid - 1);StackPush(&stack, begin);}}StackDestroy(&stack);
}就是利用栈来存每次递归的区间用栈模拟实现递归过程注意的是每次入栈应该是右区间先入再左区间
3.2.2 快速排序的特性
4. 归并排序
4.1 归并递归实现
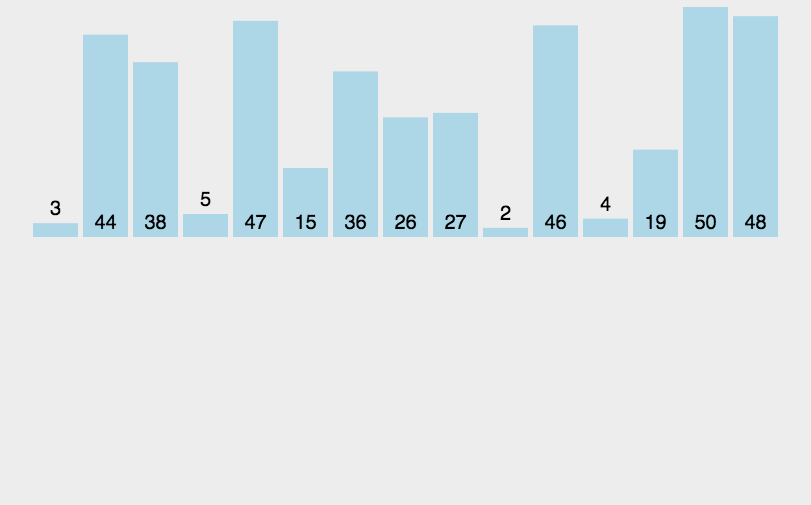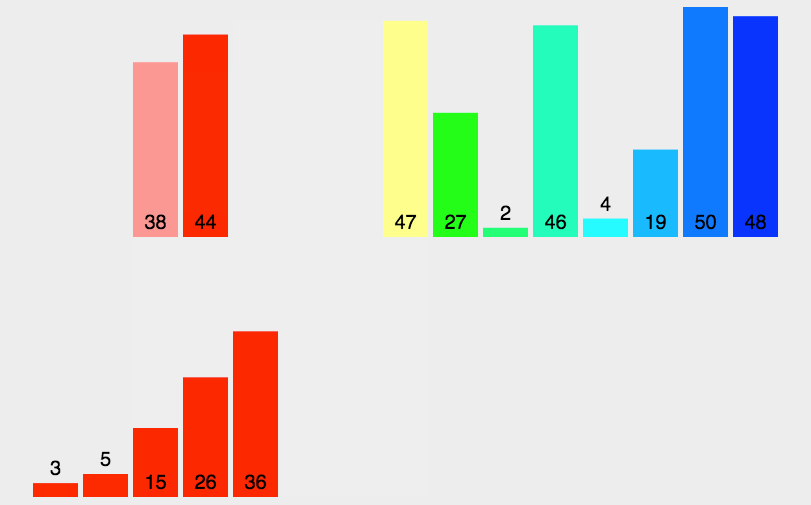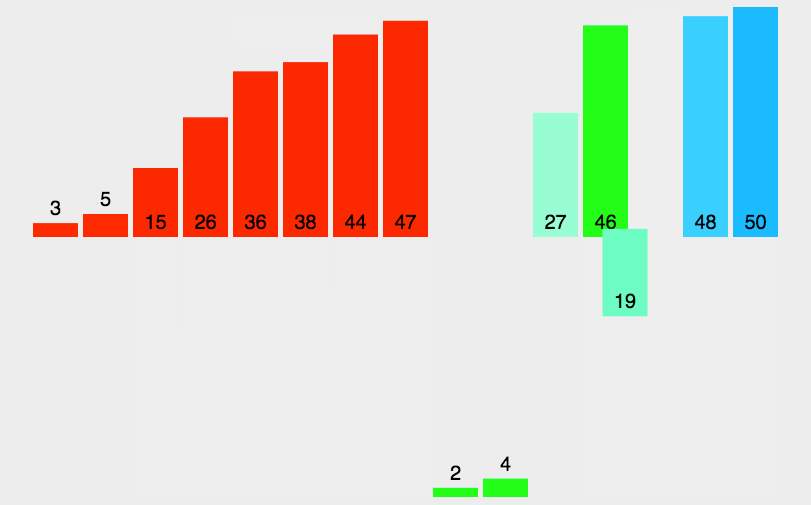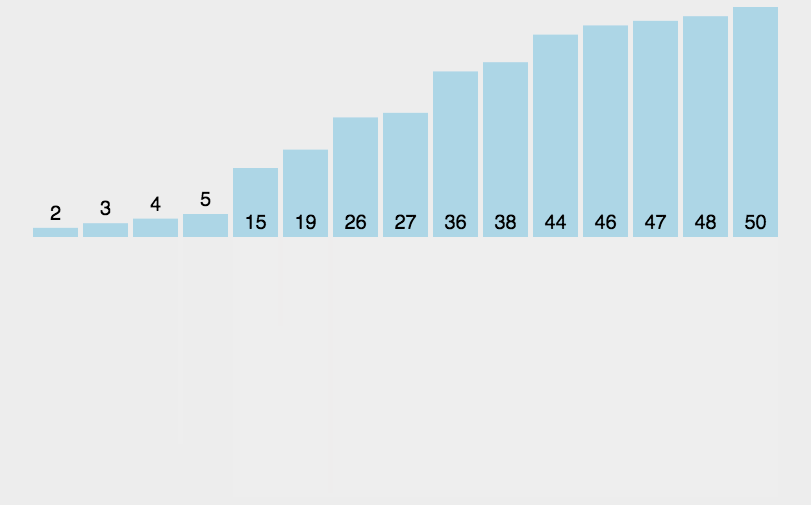
void _MergeSort(int *a, int *tem, int left, int right)
{if (left >= right){return;}int mid = (right - left) / 2 + left;_MergeSort(a, tem, left, mid);_MergeSort(a, tem, mid+1, right);//下面要进行归并排序int j = left;int begin1 = left;int end1 = mid;int begin2 = mid + 1;int end2 = right;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tem[j++] = a[begin1++];}else{tem[j++] = a[begin2++];}}while (begin1 <= end1){tem[j++] = a[begin1++];}while (begin2 <= end2){tem[j++] = a[begin2++];}memcpy(a + left, tem + left, sizeof(int) * (right - left + 1));
}
//归并排序
void MergeSort(int* a, int n)
{int* tem = (int*)malloc(sizeof(int) * n);int left = 0;int right = n - 1;_MergeSort(a, tem, left, right);
}注意分区间为什么是以上的分法请看下图

如果[2,3]按照第一种则会一直递归造成栈溢出。
4.2 归并非递归实现
//归并排序非递归写法
void MergeSortNonR(int *a, int n)
{int* tem = (int*)malloc(sizeof(int) * n);if (tem == NULL){perror("malloc faliue");return;}int gap = 1;while (gap <= n){//gap是每组归并数据的数据个数for (int i = 0; i < n; i += 2 * gap){int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;//第二组全都越界if (begin2 >= n){break;}//第二组部分越界end2更新if (end2 >= n)end2 = n - 1;int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tem[j++] = a[begin1++];}else{tem[j++] = a[begin2++];}}while (begin1 <= end1){tem[j++] = a[begin1++];}while (begin2 <= end2){tem[j++] = a[begin2++];}memcpy(a + i, tem + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}free(tem);tem == NULL;
}这里我们注意的就是越界问题如果begin2越界说明此次归并不需要了end2越界说明第二组有部分数据需要归并end2更新。如果end1越界此时begin2一定越界直接退出for循环不用进行归并了
5. 非比较排序
5.1 计数排序
代码实现:其实就是一个简单的哈希映射
// 计数排序
void CountSort(int* a, int n)
{//申请一个计数数组int max = a[0];int min = a[0];for (int i = 0; i < n; i++){if (a[i] > max){max = a[i];}if (a[i] < min){min = a[i];}}int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));for (int i = 0; i < n; i++){count[(a[i]-min)]++;}int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}free(count);count = NULL;
}5.2 基数排序

思想就是先按照最低位按照顺序先排接着一直到最高位这里我们只需要了解一下思想就行
5.3 桶排序
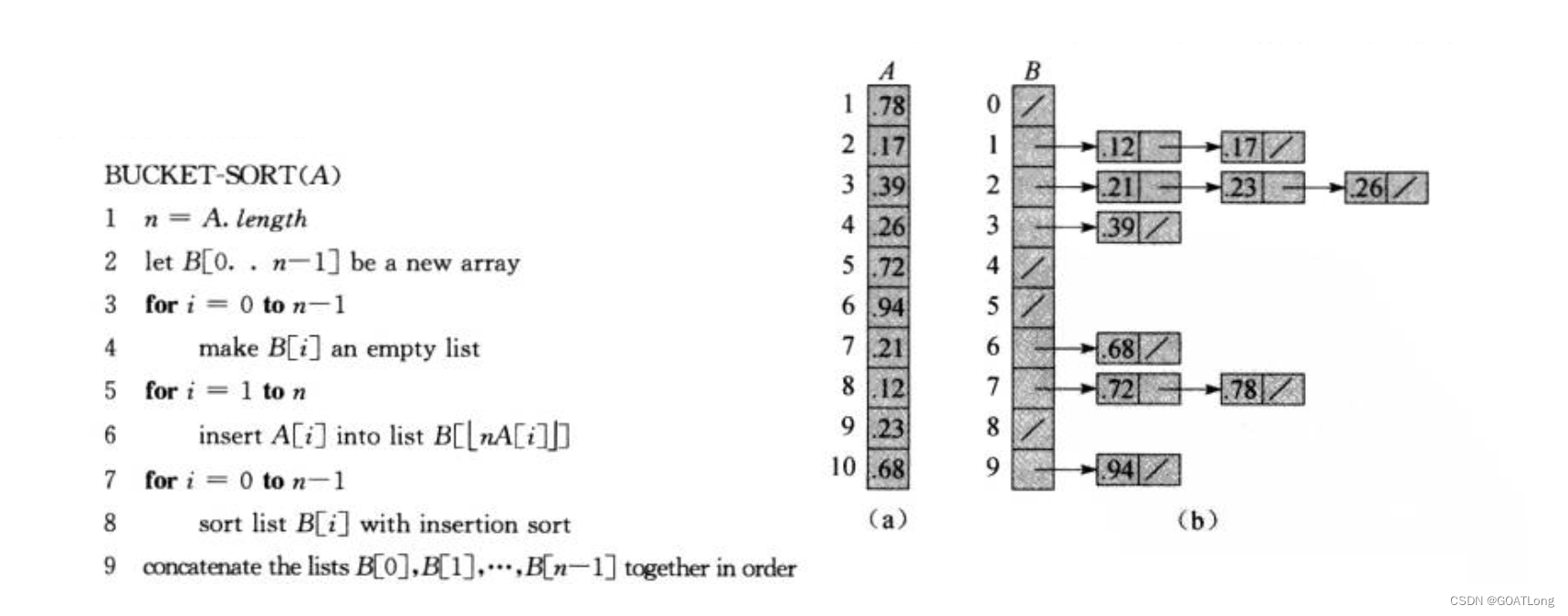
思想就是我们建立一个指针数组此时数组里面的元素是一个指向链表结点的指针。
我们便利原数组把最高位对应的数放到指针数组对应的下标比如78,就要放到B数组下标为7的那个数组元素里面如果再来一个76就进行尾插最后对链表排序。
6. 排序算法复杂度及稳定性
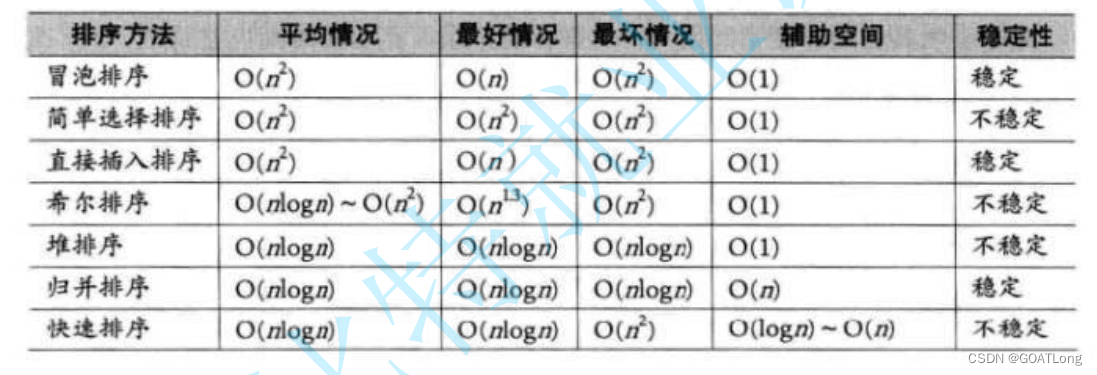
稳定性是指两个相同的数在排序前后的相对位置如果不变就是稳定反之则不稳定。
冒泡这里我们这里我们不分析了
选择排序假设6,6,2我们把6和2交换6的相对位置改变了就不稳定了
插入排序是稳定
希尔如果两个相同的数被分到不同的组就会不稳定
堆排如果都是2把2放到最后相对位置改变不稳定
归并排序就是我们在归并时如果相等我们就把左区间的那个值先放到数组中就稳定了
快速排序假设6,6,5我们把6和5交换就会不稳定了
相关文章:

数据结构之排序算法
目录 1. 插入排序 1.1.1 直接插入排序代码实现 1.1.2 直接插入排序的特性总结 1.2.1 希尔排序的实现 1.2.2 希尔排序的特性总结 2. 选择排序 2.1.1 选择排序 2.1.2 选择排序特性 2.2.1 堆排序 2.2.2 堆排序特性 3. 交换排序 3.1.1 冒泡排序 3.1.2 冒泡排序的特性 …...

移动安全赋能化工能源行业智慧转型
随着我国能源化工企业的不断发展,化工厂中经常存在火灾爆炸的危险,特别是生产场所,约有80%以上生产场所区域存在爆炸性物质。而目前我国化工危险场所移动通信设备的普及率高,但是对移动通信设备的安全防护却有所忽视,包…...

今天是放假带娃的一天
端午节放假第一天 早上5点半宝宝就咔咔乱叫了,几乎每天都这个点醒,准时的很,估计他是个勤奋的娃吧,要早起锻炼婴语,哈哈 醒来后做饭、洗锅、洗宝宝的衣服、给他吃D3,喂200ml奶粉、给他洗澡、哄睡࿰…...

linux Ubuntu安装samba服务器与SSH远程登录
目录 1,下载安装包 2,添加服务器 3,修改服务器配置 3.1 备份配置文件 3.2 修改配置 4,开启samba服务器 5,开关电脑与服务器设置 6, SSH远程登录 1,下载samba服务器安装包 sudo apt in…...
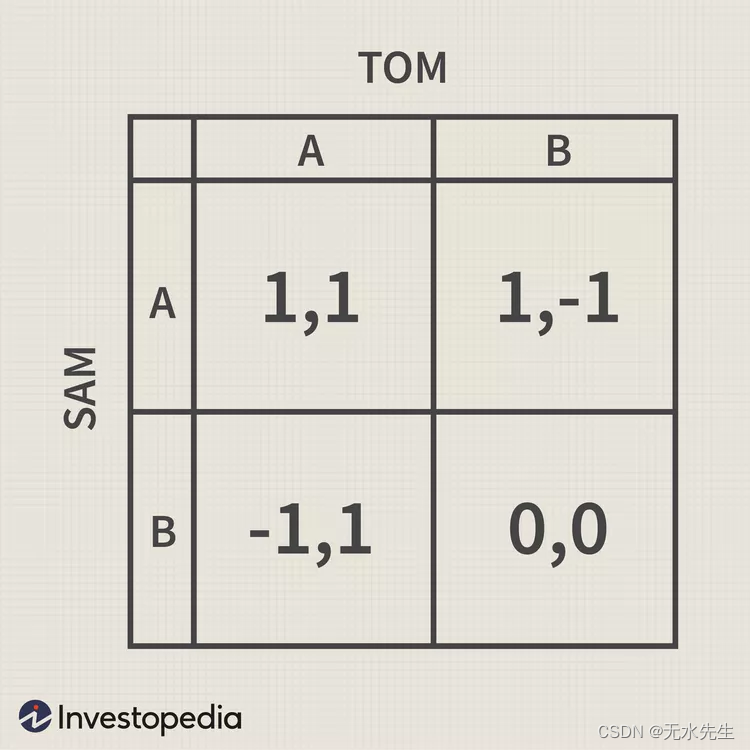
纳什均衡:博弈论中的运作方式、示例以及囚徒困境
文章目录 一、说明二、什么是纳什均衡?2.1 基本概念2.2 关键要点 三、理解纳什均衡四、纳什均衡与主导策略五、纳什均衡的例子六、囚徒困境七、如何原理和应用7.1 博弈论中的纳什均衡是什么?7.2 如何找到纳什均衡?7.3 为什么纳什均衡很重要&a…...

Linux之进程信号详解【上】
🌎 Linux信号详解 文章目录: Linux信号详解 信号入门 技术应用角度的信号 信号及信号的产生 信号的概念 信号的处理方式 信号的产生方式 键盘产生信号 系统调用产生信号 软件…...

【Spring Cloud】Eureka详细介绍及底层原理解析
目录 底层原理详解 1. 服务注册与发现 2. 心跳机制 3. 服务剔除与自我保护机制 Eureka Server 核心组件 Eureka Client 核心组件 使用场景 结语 Eureka 是 Netflix 开源的一款服务发现框架,用于构建分布式系统中的服务注册与发现。 它包含两个核心组件&…...
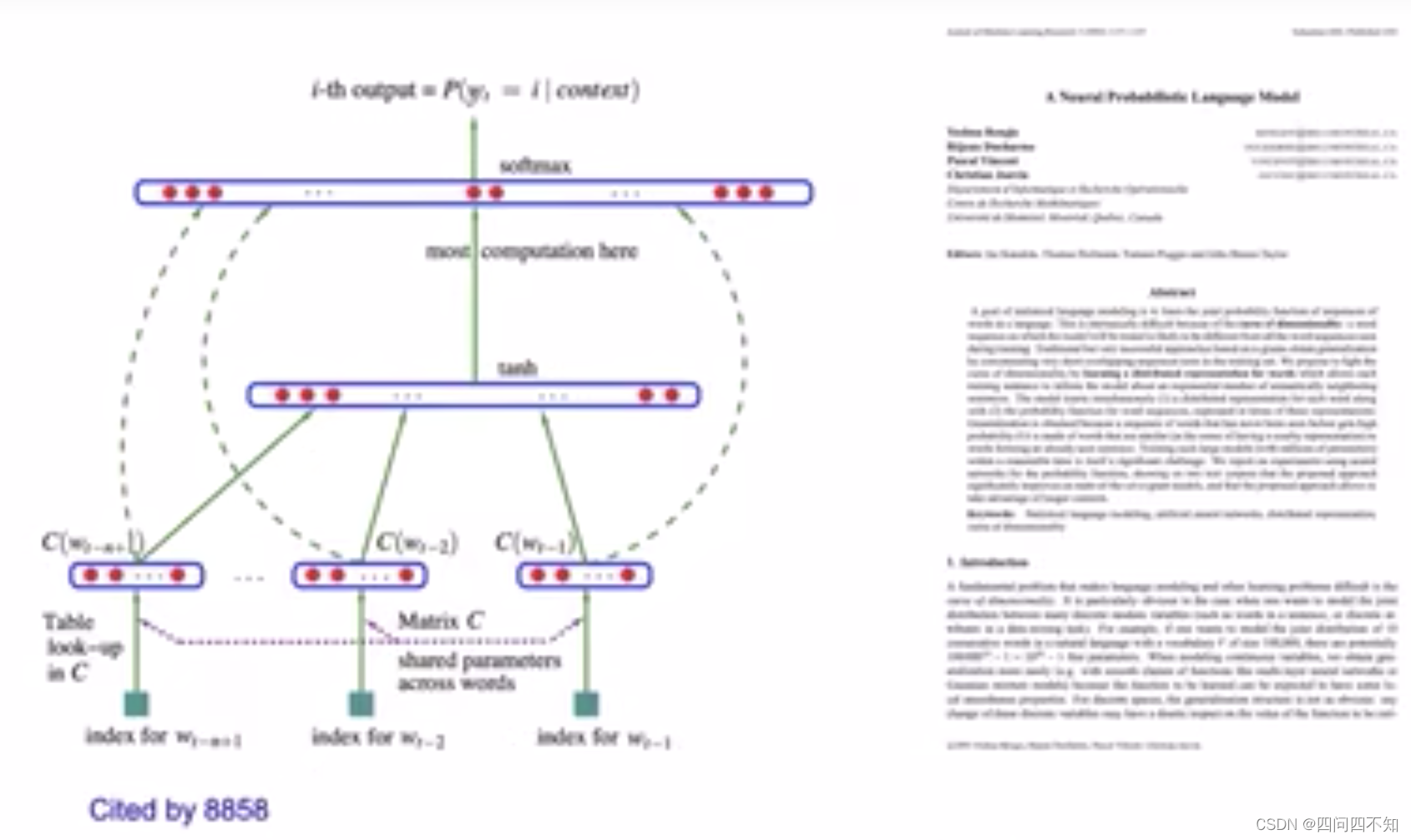
【清华大学】《自然语言处理》(刘知远)课程笔记 ——NLP Basics
自然语言处理基础(Natural Language Processing Basics, NLP Basics) 自然语言处理( Natural Language Processing, NLP)是计算机科学领域与人工智能领域中的一个重要方向。它研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。自然语言…...

代码随想录 | Day17 | 二叉树:二叉树的最大深度最小深度
代码随想录 | Day17 | 二叉树:二叉树的最大深度&&最小深度 主要学习内容: 利用前序后序层序求解二叉树深度问题 其中穿插回溯法 104.二叉树的最大深度 104. 二叉树的最大深度 - 力扣(LeetCode) 递归遍历 后序遍历 …...

【Linux】Socket编程基础
文章目录 字节序字节序转化函数 套接字socket通用结构体通信类型名空间套接字函数socket():创建套接字bind()函数:绑定服务器套接字与其地址、端口listen()函数:侦听客户连接connect():连接服务器套接字accept()函数:服…...
关于stm32的软件复位
使用软件复位的目的: 软件复位并不会擦除存储器中的数据,它只是将处理器恢复到复位状态,即中断使能位被清除,系统寄存器被重置,但RAM和Flash存储器中的数据保持不变。 STM32软件复位(基于库文件V3.5) ,对…...

规范系统运维:系统性能监控与优化的重要性与实践
在当今这个高度信息化的时代,企业的IT系统运维工作显得尤为关键。其中,系统性能监控和优化是运维工作中不可或缺的一环。本文旨在探讨规范系统运维中系统性能监控与优化的重要性,并分享一些实践经验和策略。 一、系统性能监控与优化的重要性…...

用python编撰一个电脑清理程序
自制一个电脑清理程序,有啥用呢?在电脑不装有清理软件的时候,可以解决自己电脑内存不足的情况。 1、设想需要删除指定文件夹中的临时文件和缓存文件。以下是代码。 import os import shutil def clean_folder(folder_path): for root,…...

2024年【天津市安全员C证】免费试题及天津市安全员C证试题及解析
题库来源:安全生产模拟考试一点通公众号小程序 天津市安全员C证免费试题是安全生产模拟考试一点通生成的,天津市安全员C证证模拟考试题库是根据天津市安全员C证最新版教材汇编出天津市安全员C证仿真模拟考试。2024年【天津市安全员C证】免费试题及天津市…...
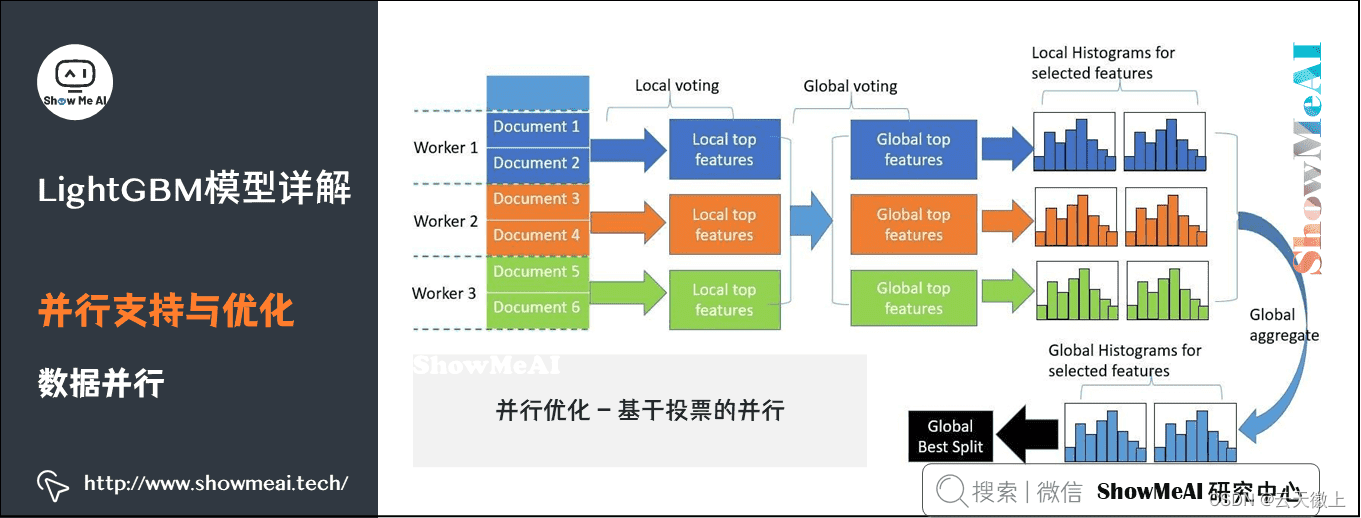
【Python数据挖掘实战案例】机器学习LightGBM算法原理、特点、应用---基于鸢尾花iris数据集分类实战
一、引言 1、简要介绍数据挖掘的重要性和应用 在数字化时代,数据已经成为企业和社会决策的重要依据。数据挖掘作为一门交叉学科,结合了统计学、机器学习、数据库技术和可视化等多个领域的知识,旨在从海量数据中提取有价值的信息,…...
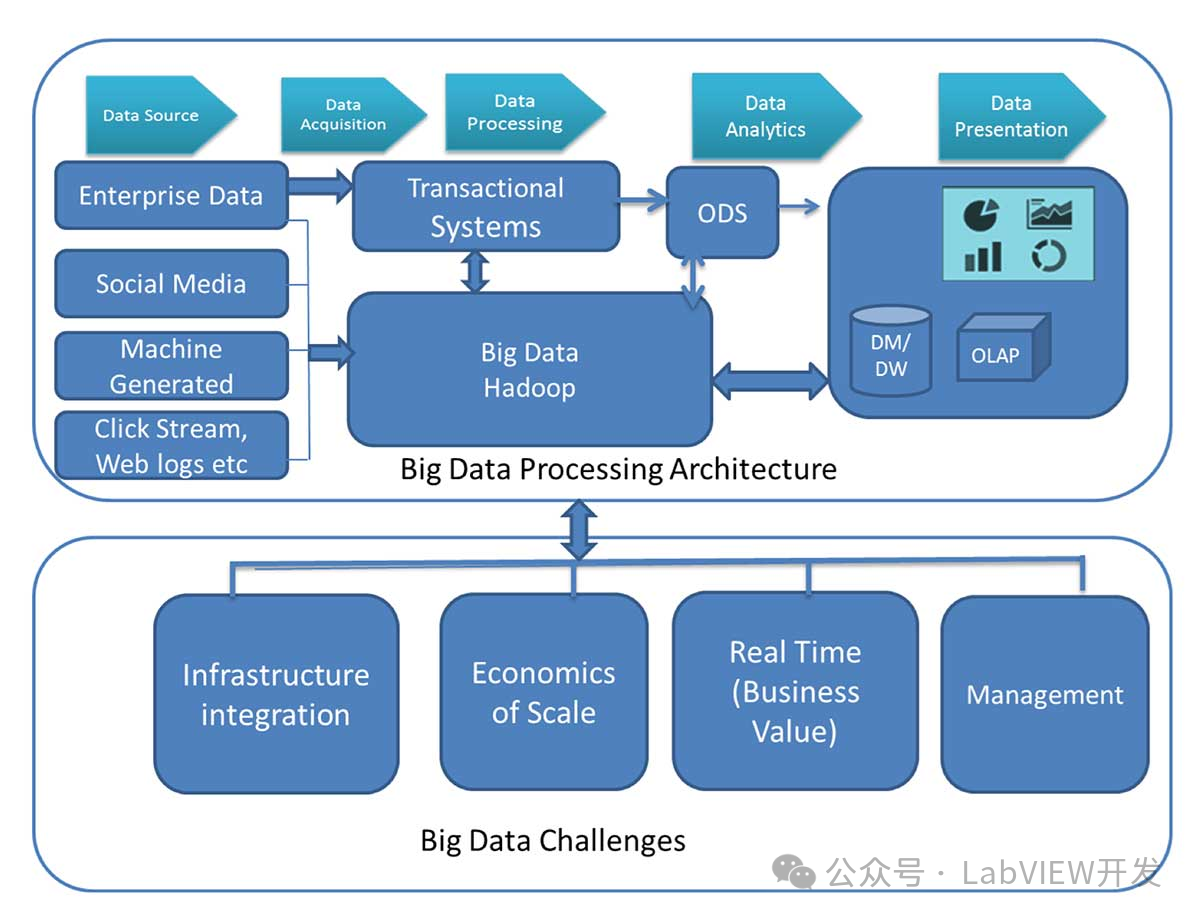
使用LabVIEW进行大数据数组操作的优化方法
针对大数据量数组操作,传统的内存处理方法可能导致内存不足。通过LabVIEW的图像批处理技术,可以有效地进行大数据数组操作,包括分块处理、并行处理和内存优化等。这种方法能显著提高处理效率和系统稳定性。 图像批处理的优势 内存优化&#…...
【Linux】(五)—— SSH远程登录和XShell使用
SSH Linux中的SSH(Secure Shell)是一个强大的网络协议,用于在不安全的网络环境中提供安全的远程登录和资料拷贝等其他网络服务。以下是有关Linux中SSH的关键点和操作指南: SSH的基础概念 安全性:SSH通过对所有传输的…...

前端怎么实现跨域请求?
前端实现跨域请求(Cross-Origin Resource Sharing, CORS)通常涉及到后端服务器的配置,因为浏览器的同源策略(Same-Origin Policy)会阻止前端代码直接发起跨域请求。然而,有几种方法可以在前端和后端的配合下…...

sqlmap直接嗦 dnslog注入 sqllibs第8关
dnslog注入是解决注入的时候没有回显的情况,通过dns外带来进行得到我们想要的数据。 我们是用了dns解析的时候会留下记录,这时候就可以看见我们想要的内容。 这个时候我们还要了解unc路径以及一个函数load_file()以及concat来进行注入。看看我的笔记 unc…...

数据结构笔记 3 串 数组 广义表
以下了解即可,暂时没发现有什么考点 参考: 【数据结构】——多维数组和广义表_数据结构loc-CSDN博客 相对应的题目: 他这个数组不是从0开始的,是从1开始的,所以为了配合公式要减1 下面这道题又不一样,它是…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
