常见排序算法,快排,希尔,归并,堆排
后面的排序中都要用到的函数
//交换
void Swap(int* p1, int* p2)
{int* tmp = *p1;*p1 = *p2;*p2 = tmp;
}包含的头文件 "Sort.h"
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<time.h>
#include<string.h>//交换
void Swap(int* p1, int* p2);
//向下调整,parent和child都是指下标,n指要调整的所有数据的上限下标
void AdjustDown(int* arr, int n, int parent);
//堆排序
void HeapSort(int* a, int n);// 插入排序
void InsertSort(int* a, int n);// 希尔排序
void ShellSort(int* a, int n);// 选择排序
void SelectSort(int* a, int n);// 冒泡排序
void BubbleSort(int* a, int n);// 快速排序递归实现
// 快速排序hoare版本
//left:区间的左端点,right:区间的右端点(都是指下标)
int QuickSort(int* a, int left, int right);// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right);//归并排序,n是数组长度
void MergeSort(int* a, int n);
//归并排序非递归实现
void MergeSortNonR(int* a, int n);一.冒泡排序
// 冒泡排序
void BubbleSort(int* a, int n)
{//单趟:把最大的数换到最后for (int i = 0; i < n; i++){//如果一趟走完没有发生交换,说明已经有序int flag = 1;for (int j = 0; j < n - i - 1; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);flag = 0;}}if (flag == 1)return;}
}二.选择排序
// 选择排序
void SelectSort(int* a, int n)
{int begin = 0;int end = n-1;while(begin < end){int mini = begin;int maxi = end;//二者都是下标//[i,n]中选出最大,和最小的数,分别放到begin,end的位置for (int i = begin; i <= end; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[begin], &a[mini]);//maxi可能和begin重叠,此时maxi换到了mini位置if (maxi == begin)maxi = mini;Swap(&a[end], &a[maxi]);begin++;end--;}
}三.插入排序
// 插入排序,O(N^2)
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){//把a[end+1]插入到[0,end]的位置int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];//大的数往后挪end--;}else{break;}//出循环有两种情况://1.end = -1,即tmp比[0,end]之间的数都要小//2.a[end]<tmpa[end + 1] = tmp;}}
}四.堆排
//向下调整,parent和child都是指下标,n指要调整的所有数据的上限下标
void AdjustDown(int* arr, int n, int parent)
{int child = parent * 2 + 1;while (child < n)//child >= n,说明孩子不存在{//建小堆(建大堆:表示比较关系的"<",">"全部取反)//假设法,假设左孩子小if (arr[child + 1] < arr[child] && (child + 1) < n)//防止child+1越界{child++;}if (arr[parent] > arr[child]){Swap(&arr[parent], &arr[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* a, int n)
{assert(a);//1.向下调整建堆(小堆)int i = 0;for (i = (n - 1 - 1) / 2; i >= 0; i--)//n-1是最后一个数据的下标,(n-1-1)/2是最后一个非叶子节点{AdjustDown(a, n, i);}//2.堆顶的数据和最后一个数据进行交换,调整完的数据向下调整,再将钱n-1个数据看做一个新堆//堆顶(最小的)数据放到数据末尾,第二小的放到倒数第二位,依次进行int end = n - 1;while (end > 0){//交换Swap(&a[0], &a[end]);//调整AdjustDown(a, end, 0);end--;}
}五.希尔排序
// 希尔排序,时间复杂度O(N^1.3)
void ShellSort(int* a, int n)
{//1.分gap组int gap = n;while (gap > 1){// +1保证最后一个gap一定是1// gap > 1时是预排序// gap == 1时是插入排序gap = gap / 3 + 1;//2.多个gap组并行for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];//大的数往后移end -= gap;//一次跳gap步}else{break;}a[end + gap] = tmp;}}}
}六.快速排序(快排)
三数取中
int Getmidi(int*a,int left,int right)
{int midi = (right + left) / 2;//左<中if (a[left] < a[midi]){//中>右,中是最大的if (a[midi] > a[right]){//左<右<中if (a[left] < a[right]){return right;}else//右<左<中{return left;}}else//左<中<右{return midi;}}else//左>中{//中<左,中<右if (a[midi] < a[right]){//中<左<右if (a[left] < a[right]){return left;}else//中<右<左{return right;}}else//右<中<左{return midi;}}
}1.快排单趟的不同版本
1.1 hoare版本
//单趟(hoare版本)
int partsort1(int*a,int left,int right)
{//优化——keyi的选择:// 如果数据是有序的,此时再选left位置的数当作keyi,则分割的区间就会变成0+n-1,时间复杂度退化为O(N^2)//解决方法——三数取中:选left,right,midi(区间中间位置的数)中,中间大小的数) int midi = Getmidi(a, left, right);Swap(&a[midi], &a[left]);int keyi = left;int begin = left;int end = right;while (begin < end){//左边找大,右边找小//begin<end 这个条件要加上,否则在找大(或找小)的过程中,begin可能越过了endwhile (begin < end && a[begin] < a[keyi]){++begin;}while (begin<end && a[end]>a[keyi]){--end;}//begin和end停下后,交换,把比a[keyi]大的数放右边,小的数放左边Swap(&a[begin], &a[end]);}//begin和end相遇的位置(记为meet)一定比a[keyi]小(该结论可证明),二者交换Swap(&a[keyi], &a[begin]);return begin;
}1.2前后指针法
//前后指针法
int partsort2(int* a, int left, int right)
{//优化——keyi的选择:// 如果数据是有序的,此时再选left位置的数当作keyi,则分割的区间就会变成0+n-1,时间复杂度退化为O(N^2)//解决方法——三数取中:选left,right,midi(区间中间位置的数)中,中间大小的数) int midi = Getmidi(a, left, right);Swap(&a[midi], &a[left]);int prev = left;int cur = prev + 1;//a[cur]<a[left],二者同时++//a[cur]<a[left],cur++,prev不动while (cur <= right){//a[cur]<a[left]时,有两种情况//prev++后,1.a[prev]<a[left] 2.a[prev]>a[left]//若是第一种情况,则二者不需要交换,且此时prev == cur//第二种情况,二者需要交换if (a[cur] < a[left] && ++prev != cur)//这里的++是前置++,能保证在第一个条件满足的前提下,prev一定向前移动{Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[prev], &a[left]);return prev;
}
2.快排的不同版本
2.1 递归版
int QuickSort(int* a, int left, int right)
{//结束条件:1.区间内只剩一个数;2.区间不存在if (left >= right)return;//优化——小区间优化:当区间<10时,再使用函数递归调用很不划算,所以改为使用插入排序if (right - left <= 10){//区间左端:a+left,大小:right - left + 1 ([0,9]是十个数)InsertSort(a + left, right - left + 1);}else{//单趟int keyi = partsort1(a, left, right);//meet将数据分割为左区间和右区间//根据二叉树的思想,使用递归,对左右区间进行同样的操作//[left,keyi-1] keyi [keyi+1,right]QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}
}2.2 非递归版
(栈实现的所有接口代码我会放在后面,也可看我之前的博客)
#include"Stack.h"
// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{//使用栈来存储区间下标ST st;STInit(&st);//栈的初始化//先入右端点,再入左端点STPush(&st, right);STPush(&st, left);//如果栈不为空,说明还有未排序的区间while(!STEmpty(&st)){int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);int keyi = partsort1(a, begin, end);//[begin,keyi-1] keyi [keyi+1,end]//先入右区间,再入左区间,先取出的就是左区间,和递归的逻辑顺序相一致//区间只有一个值或区间不存在时,不需要入栈if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi + 1);}if (begin < keyi - 1){STPush(&st, keyi - 1);STPush(&st, begin);}}STDestroy(&st);//栈的销毁
}七.归并排序
1.递归版
//归并排序
void _MergeSort(int* a, int* tmp, int begin, int end)(子函数)
{//当数据有序时,可以进行归并//当区间内只有一个数时,可看做有序,然后两两归并//函数返回后,进行四四归并if (begin >= end)return;int mid = (begin + end) / 2;_MergeSort(a, tmp, begin, mid);_MergeSort(a, tmp, mid+1,end);//归并int begin1 = begin;int begin2 = mid + 1;int i = begin;//i是tmp中的元素下标//对进行归并的两个区间进行排序,并将排序后的结果放到tmp数组中while (begin1 <= mid && begin2 <= end){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= mid){tmp[i++] = a[begin1++];}while (begin2 <= end){tmp[i++] = a[begin2++];}//将tmp数组中的数拷贝回a数组//注意拷贝范围是归并后的两个区间和memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));//[0,9]是十个数
}
//n是数组长度
void MergeSort(int* a, int n)//主函数
{//在主函数内创建数组,在子函数内实现排序算法//这样可避免在递归时,子函数重复动态申请内存的过程int* tmp = (int*)malloc(sizeof(int)*n);if (tmp == NULL){perror("malloc");return;}_MergeSort(a, tmp, 0, n - 1);free(tmp);tmp = NULL;
}2.非递归版
//归并排序非递归实现
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc");return;}int gap = 1;while (gap < n){//单趟归并//11归并,22归并,44归并//每次归并两组,一组含有gap个数,gap是2的次方倍for (int i = 0; i < n; i += 2*gap){//[begin1,end1] [begin2,end2]int begin1 = i;int end1 = begin1 + gap - 1;int begin2 = end1 + 1;int end2 = begin2 + gap - 1;//对进行归并的两个区间进行排序,并将排序后的结果放到tmp数组中//在这样的区间划分下,end1,begin2,end2都有可能会越界//修改优化:if (begin2 >= n)//begin2越界,说明end2肯定也越界了,此时不再需要归并{break;}if (end2 >= n)//走到这里说明begin2,end1都没有越界,修改end2后继续归并{end2 = n - 1;}int j = begin1;//j是tmp中的元素下标while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));//为防止越界,不能直接乘以2倍的gap}gap *= 2;}free(tmp);tmp = NULL;
}附:栈的接口代码
Stack.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>typedef int STDataType;typedef struct Stack
{STDataType* arr;//用数组来实现栈int top;int capacity;
}ST;// 初始化和销毁
void STInit(ST* pst);
void STDestroy(ST* pst);// 入栈 出栈
void STPush(ST* pst, STDataType x);
void STPop(ST* pst);// 取栈顶数据
STDataType STTop(ST* pst);// 判空
bool STEmpty(ST* pst);
// 获取数据个数
int STSize(ST* pst);Stack.c
#include"Stack.h"// 初始化和销毁
void STInit(ST* pst)
{assert(pst);pst->arr = NULL;pst->capacity = 0;pst->top = 0;//top指向栈顶元素的下一位,数组下标从0开始//top = 数据个数
}
void STDestroy(ST* pst)
{assert(pst);free(pst->arr);pst->arr = NULL;pst->capacity = 0;pst->top = 0;
}// 入栈 出栈
void STPush(ST* pst, STDataType x)
{assert(pst);if (pst->capacity == pst->top)//扩容{int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;STDataType* tmp = (STDataType*)realloc(pst->arr, newcapacity*sizeof(STDataType));if (tmp == NULL){perror("realloc");exit(1);}pst->arr = tmp;pst->capacity = newcapacity;}pst->arr[pst->top++] = x;
}
void STPop(ST* pst)
{assert(pst);assert(pst->top > 0);//栈的数据个数大于0pst->top--;
}// 取栈顶数据
STDataType STTop(ST* pst)
{assert(pst);assert(pst->top > 0);//栈的数据个数大于0return pst->arr[(pst->top - 1)];
}// 判空
bool STEmpty(ST* pst)
{assert(pst);return (pst->top == 0);
}
// 获取数据个数
int STSize(ST* pst)
{assert(pst);return pst->top ;
}
相关文章:

常见排序算法,快排,希尔,归并,堆排
后面的排序中都要用到的函数 //交换 void Swap(int* p1, int* p2) {int* tmp *p1;*p1 *p2;*p2 tmp; } 包含的头文件 "Sort.h" #pragma once #include<stdio.h> #include<stdlib.h> #include<assert.h> #include<time.h> #include<s…...
)
语法的时态1——一般现在时(1)
定义:一般现在时用来表示经常发生的动作,以及客观事实。 一般现在时的构成以及标志词 1.一般现在时的结构 (1)主系表结构 构成:主语be(am,is,ear)其他。属于状态句。 I…...
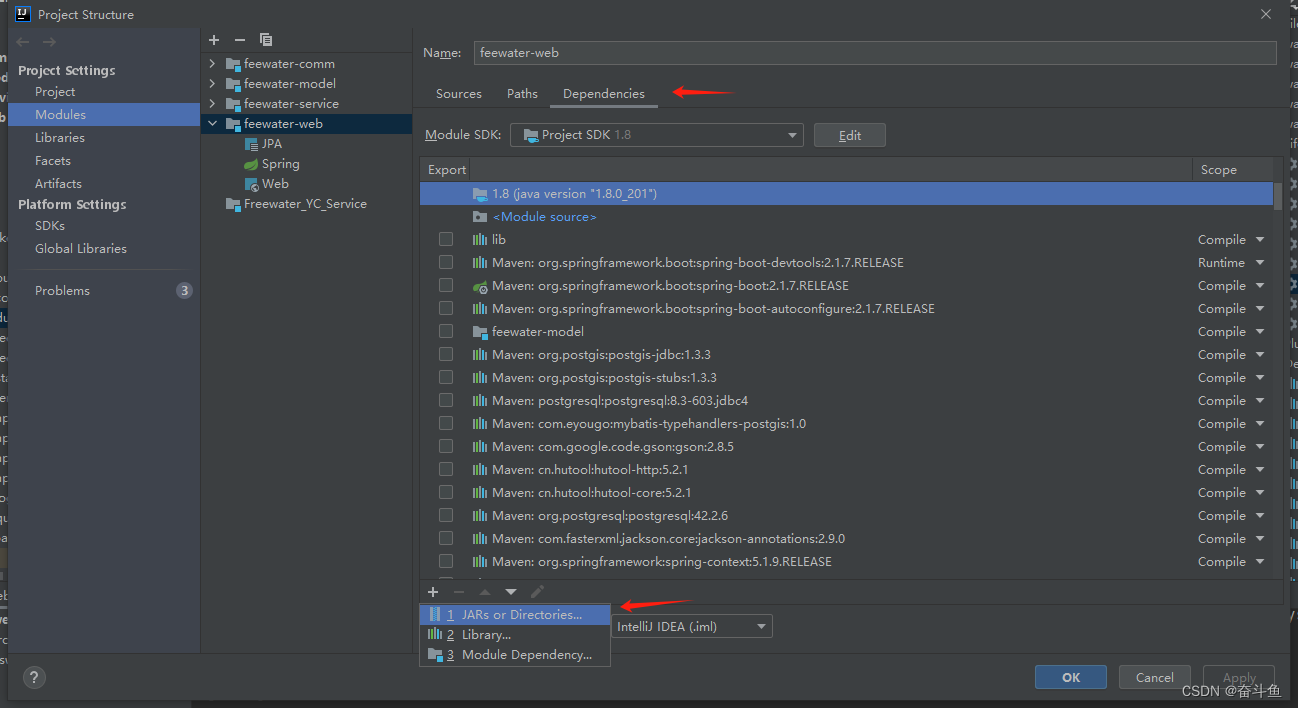
JAVA:在IDEA引入本地jar包的方法并解决打包scope为system时发布无法打包进lib的方案
一.引入本地Jar包的步骤 有时maven依耐的包是本地的jar包,此时需要进行以下步骤设置。 步骤1.在pom.xml中添加插件设置,将system范围包含进来,此设置是为了在打包时,本地jar包自动生成到部署包里。(若无法打进包,请参考下文的方…...
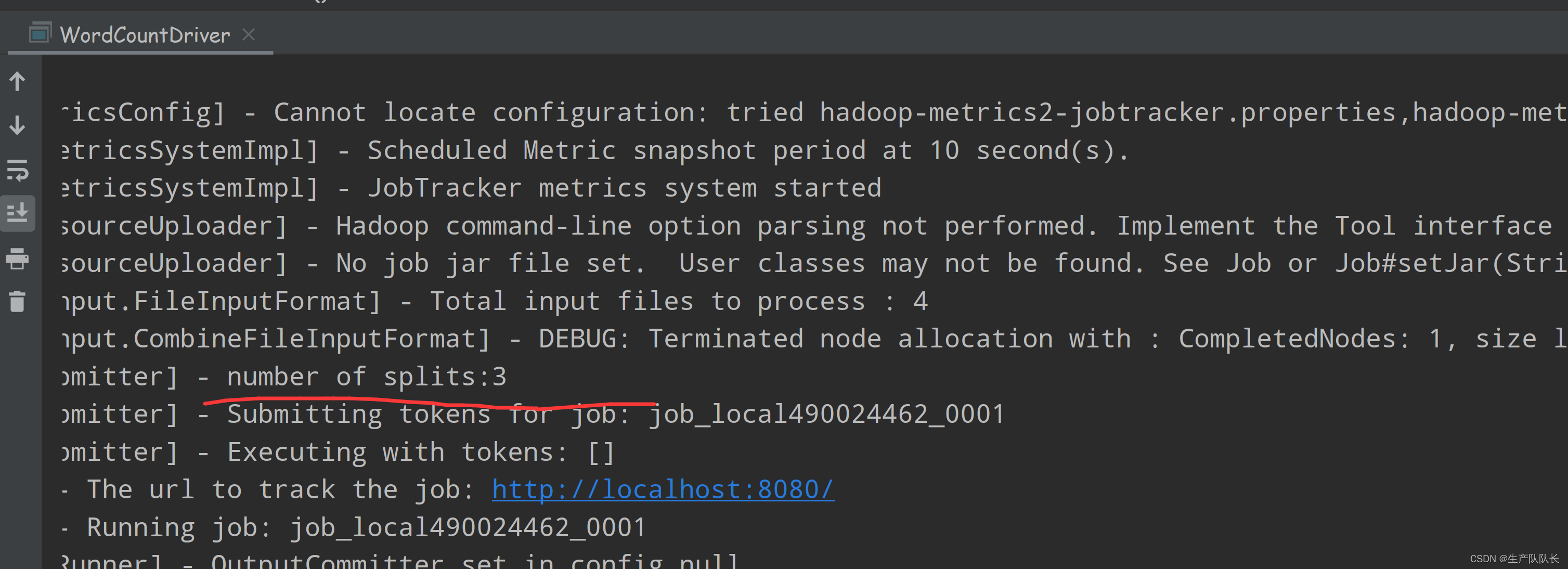
Hadoop3:MapReduce源码解读之Map阶段的CombineFileInputFormat切片机制(4)
Job那块的断点代码截图省略,直接进入切片逻辑 参考:Hadoop3:MapReduce源码解读之Map阶段的Job任务提交流程(1) 6、CombineFileInputFormat原理解析 类的继承关系 与TextInputFormat切片机制的区别 框架默认的TextI…...

GPT-4o:OpenAI的最新篇章与深度探索
引言: 在人工智能领域,自然语言处理(NLP)技术持续引领着技术创新的步伐。自2023年引入以来,GPT系列模型一直以其卓越的语言生成能力而闻名,近期的迭代——GPT-4o,更是为这一领域的研究和应用带…...

OpenGauss数据库-5.数据更新
第1关:插入数据 gsql -d postgres -U gaussdb -W "passwd123123" create table student (id integer primary key,name char(20),age integer ); insert into student values(1,"lily",20),(2,lily,21),(3,marry,19); 第2关:删除数…...
 - 三语言AC题解(Python/Java/Cpp))
【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 机场航班调度程序(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 📎在线评测链接 🌍 评测功能需要订阅专栏后私信联系清隆解锁~ 文章目录 …...

Spark作业运行异常慢的问题定位和分析思路
一直很慢 🐢 运行中状态、卡住了,可以从以下两种方式入手: 如果 Spark UI 上,有正在运行的 Job/Stage/Task,看 Executor 相关信息就好。💻 第一步,如果发现卡住了,直接找到对应的…...
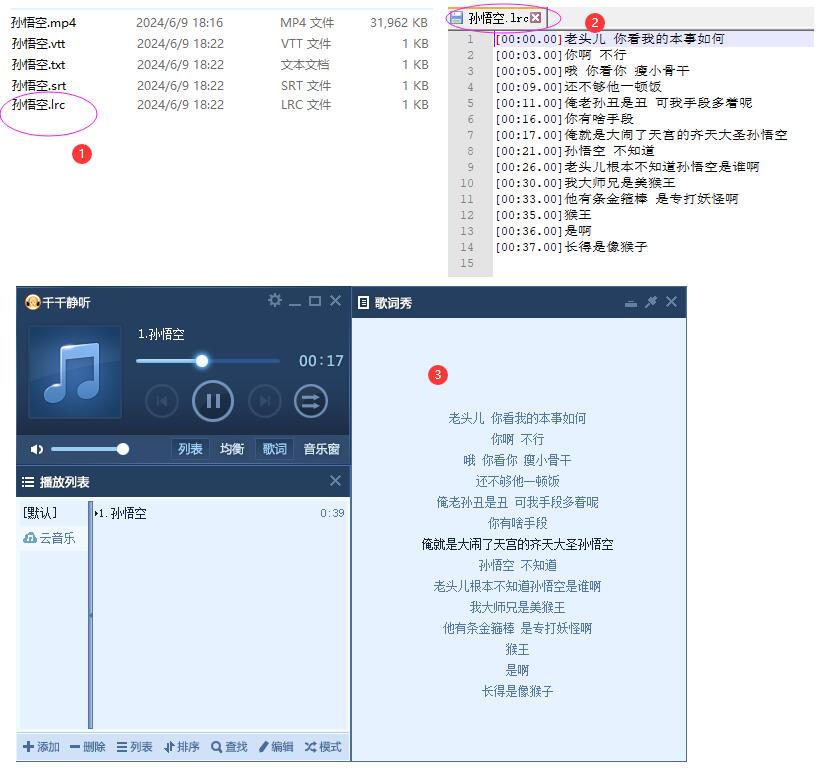
音视频转为文字SuperVoiceToText
音视频转为文字SuperVoiceToText,它能够把视频或语音文件高效地转换为文字,它是基于最为先进的 AI 大模型,通过在海量语音资料上进行训练学习而造就,具备极为卓越的识别准确率。 不仅如此,它支持包括汉语、英语、日语…...

Python基础教程(九):Lambda 函数
💝💝💝首先,欢迎各位来到我的博客,很高兴能够在这里和您见面!希望您在这里不仅可以有所收获,同时也能感受到一份轻松欢乐的氛围,祝你生活愉快! 💝Ὁ…...
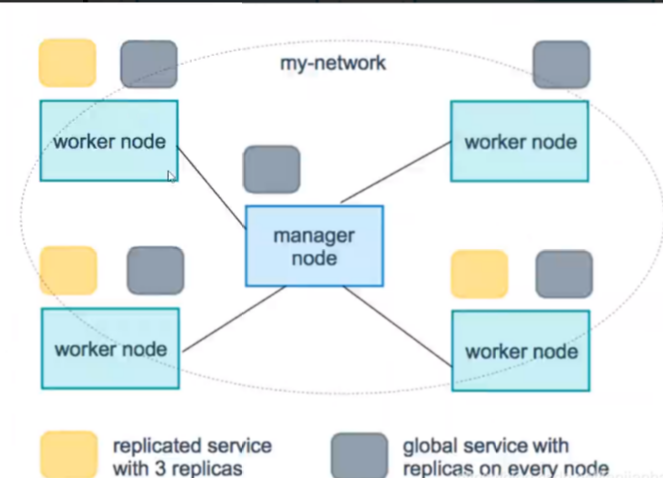
docker从入门到精通
一、Docker基本命令 1. Docker的常用命令 帮助命令 docker version # docker版本信息 docker info # 系统级别的信息,包括镜像和容器的数量 docker 命令 --help 帮助文档 镜像命令 docker images 查看所有本地主机上的镜像 [rootiZ2zeg4ytp0whqtmxbsqiiZ…...

介绍工厂模式
简单工程 public class SingleFactoryTest {public static void main(String[] args) {SingleFactory factory new SingleFactory();Product productA factory.getObject("1");productA.method();Product productB factory.getObject("2");productB.me…...

大数据领域的workload是什么意思?
什么是workload? 在大数据领域,"workload"指的是需要处理的数据集和对其执行的操作的组合。它描述了大数据系统需要执行的任务的类型和规模。 我们可以从以下几个维度来理解大数据领域的 workload: 数据的特征: 数据量 需要处…...

引入别人的安卓项目报错
buildscript { repositories { google() jcenter() } dependencies { classpath com.android.tools.build:gradle:4.1.0 // 使用最新版本的插件 } } allprojects { repositories { google() jcenter() } } 在…...
Python Excel 指定内容修改
需求描述 在处理Excel 自动化时,财务部门经常有一个繁琐的场景,需要读取分发的Excel文件内容复制到汇总Excel文件对应的单元格内,如下图所示: 这种需求可以延申为,财务同事制作一个模板,将模板发送给各员工,财务同事需收取邮件将员工填写的excel文件下载到本机,再类似…...

【力扣高频题】003.无重复字符的最长子串
前段时间和小米的某面试官聊天。因为我一直在做 算法文章 的更新,就多聊了几句算法方面的知识。 并且在聊天过程中获得了一个“重要情报”:只要他来面试,基本上每次的算法题,都会去考察关于 子串和子序列 的问题。 的确…...
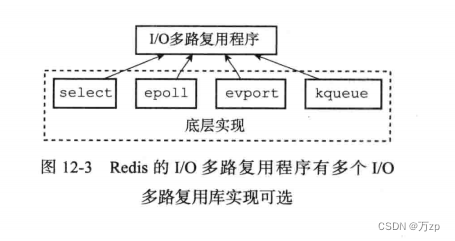
redis03 补充 事件
1.文件事件...

绿联Nas docker 中 redis 老访问失败的排查
部署了一些服务,老隔3-5 天其他服务就联不上 redis 了,未确定具体原因,只记录观察到的现象 宿主机访问 只有 ipv6 绑定了,ipv4 绑定挂掉了 其他容器访问 也无法访问成功 当重启容器后: 一切又恢复正常。 可能的解…...
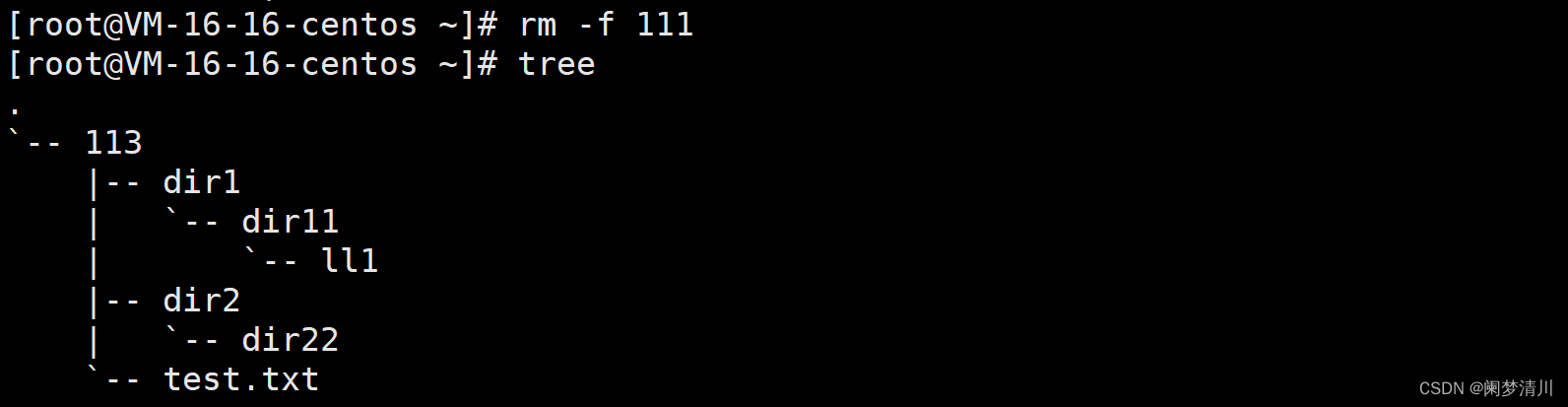
Linux入门学习(2)
1.相关复习新的指令学习 (1)我们需要自己创建一个用户,这个用户前期可以是一个root用户,后期使用创建的普通用户 (2)文件等于文件内容加上文件属性,对于文件的操作就包括对于文件内容的操作和文件属性&…...

Spring boot开启跨域配置
Spring boot开启跨域配置 背景 跨域(Cross-Origin)是指在互联网上的一个域下的文档或脚本尝试请求另一个域下的资源时,域名、协议或端口不同的这种情况。具体来说,如果一个网页试图通过脚本(如JavaScript)…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
