归并排序——逆序数对的统计
逆序数对的统计
题目描述

运行代码
#include <iostream>
using namespace std;
#define LL long long
const int N = 1e5 + 5;
int a[N], tmp[N];
LL merge_sort(int q[], int l, int r)
{if (l >= r)return 0; int mid = l + r >> 1; LL res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r); int k = 0, i = l, j = mid + 1;while (i <= mid && j <= r)if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];else{res += mid - i + 1;tmp[k ++ ] = q[j ++ ];}while (i <= mid)tmp[k ++ ] = q[i ++ ];while (j <= r)tmp[k ++ ] = q[j ++ ];for (i = l, j = 0; i <= r; i ++, j ++ )q[i] = tmp[j]; return res;
}
int main()
{int n;scanf("%d", &n);for (int i = 0; i < n; i ++ )
scanf("%d", &a[i]); cout << merge_sort(a, 0, n - 1) << endl; return 0;
}
代码思路
宏定义与常量
#define LL long long:定义LL为long long类型的别名,用于存储较大的整数,例如逆序对的数量。const int N = 1e5 + 5;:定义数组的最大容量,适用于最多100,005个元素的数组。
函数merge_sort此函数递归地将数组分成更小的部分,然后合并这些部分,同时计算逆序对总数。
- 参数:
q[]是要排序的数组,l和r分别是当前子数组的左右边界(索引)。 - 基础情况:当左边界大于等于右边界时(即子数组只有一个或没有元素),返回0,表示该子数组没有逆序对。
- 分解:计算中间索引
mid,递归地对左右两部分[l, mid]和[mid+1, r]进行排序并计算逆序对,将结果累加到res中。 - 合并:
- 初始化辅助数组
tmp和三个指针k, i, j。当i未超过mid且j未超过r时,比较q[i]和q[j]的大小:- 如果
q[i] <= q[j],说明当前元素不会形成新的逆序对,将q[i]放入tmp,并移动i和k。 - 否则,所有
q[i]到q[mid]之间的元素都比q[j]大,因此增加了mid - i + 1个逆序对,将q[j]放入tmp,移动j和k。
- 如果
- 分别处理剩余的元素,将它们依次放入
tmp。将tmp中的元素复制回原数组q。
- 初始化辅助数组
- 返回值:最终返回整个数组排序过程中的逆序对总数
res。 - 主函数
main:读取数组长度n。通过循环读取数组a中的每个元素。调用merge_sort函数,传入数组a和其边界(0和n-1),输出计算得到的逆序对总数。
改进思路
- 使用指针直接操作数组:在
mergeSortAndCount函数中,直接使用指针i,j,k而非索引,这在某些情况下可以略微提高访问效率。 - 保持数组作为参数:继续使用原生数组作为函数参数,保持与原始代码结构的一致性。
- 代码格式和可读性:调整代码格式,确保良好的可读性和一致性,比如增加必要的空格和换行。
- 去除不必要的类型别名:保留
int64_t作为长整型的别名,因为它清晰地表达了数据类型的目的。
改进代码
#include <iostream>
using namespace std;
typedef long long int64_t;
// 使用指针代替数组索引来优化访问速度
int64_t mergeSortAndCount(int a[], int temp[], int left, int right) {if (left >= right) return 0; int mid = left + (right - left) / 2; // 递归排序并计数int64_t inv_count = mergeSortAndCount(a, temp, left, mid);inv_count += mergeSortAndCount(a, temp, mid + 1, right); // 合并阶段计算逆序对int i = left, j = mid + 1, k = left;while (i <= mid && j <= right) {if (a[i] <= a[j]) {temp[k++] = a[i++];} else {inv_count += mid - i + 1;temp[k++] = a[j++];}} // 复制剩余元素while (i <= mid) temp[k++] = a[i++];while (j <= right) temp[k++] = a[j++]; // 将排序结果复制回原数组for (int p = left; p <= right; ++p) a[p] = temp[p]; return inv_count;
}
int main() {const int N = 1e5 + 10;int a[N], temp[N];int n;scanf("%d", &n); for (int i = 0; i < n; ++i) scanf("%d", &a[i]); int64_t inv_count = mergeSortAndCount(a, temp, 0, n - 1);cout << inv_count << endl; return 0;
}其他方法(使用向量) AI生成
#include <iostream>
#include <vector>using namespace std;
using int64_t = long long;// 合并排序并计数逆序对
int64_t mergeSortAndCount(vector<int>& array, vector<int>& temp, int left, int right) {if (left >= right) return 0;int mid = left + (right - left) / 2;// 递归排序左右两边,并计算逆序对int64_t inv_count = mergeSortAndCount(array, temp, left, mid);inv_count += mergeSortAndCount(array, temp, mid + 1, right);// 合并阶段计算逆序对int i = left, j = mid + 1, k = 0;while (i <= mid && j <= right) {if (array[i] <= array[j]) {temp[k++] = array[i++];} else {inv_count += mid - i + 1; // 计算逆序对temp[k++] = array[j++];}}// 处理剩余元素while (i <= mid) temp[k++] = array[i++];while (j <= right) temp[k++] = array[j++];// 将排序结果复制回原数组copy(temp.begin(), temp.begin() + k, array.begin() + left);return inv_count;
}int main() {int n;cin >> n;vector<int> a(n);for (int& elem : a) cin >> elem;vector<int> temp(n); // 临时数组用于合并cout << mergeSortAndCount(a, temp, 0, n - 1) << endl;return 0;
}- 添加函数注释:解释每个函数的作用,特别是
merge_sort中的逻辑。 - 使用更明确的变量名:如将
q[]改为array[],使代码意图更清晰。 - 去除全局变量:尽量减少全局变量的使用,改用函数参数传递。
- 优化类型别名的可读性:将
LL改为更明确的别名,如typedef long long int64_t; - 使用C++风格的输入输出:完全替换
scanf和printf为cin和cout。
归并、插入和冒泡排序比较
归并排序:
- 优点:时间复杂度在平均和最坏情况下都为 ,性能比较稳定,适合大规模数据排序。
- 缺点:需要额外的空间用于合并。
插入排序:
- 优点:对于接近有序的数据表现非常好,在小规模数据或部分有序数据上效率可能较高,代码简单。
- 缺点:最坏情况时间复杂度为 。
冒泡排序:
- 优点:实现简单。
- 缺点:时间复杂度较差,也是 。
一般来说,在数据规模较大且对性能要求较高时,归并排序通常表现更好。但如果数据规模较小或者数据有一定的特殊性(如接近有序),插入排序可能更合适。而冒泡排序相对来说在大多数情况下效率较低,较少被优先选用。
使用归并排序解决逆序数对统计问题思路:
在归并排序的合并过程中,当我们比较左右两部分元素时,左边部分一个较大元素如果出现在右边部分较小元素之前,那么就构成一个逆序数对。
当左边当前元素大于右边当前元素时,由于左右两边都是已排序的,那么左边该元素之后的所有元素与右边当前元素都构成逆序数对,数量为左边当前未处理元素的数量。我们可以在合并的同时统计这样的逆序数对数量。通过递归地执行归并排序,不断在合并过程中累加逆序数对的数量,最终就能得到总的逆序数对数量。
例如,假设有数组 [3, 1, 4, 2],在第一次合并 [3] 和 [1] 时,因为 3 大于 1,此时就找到一个逆序数对,然后继续递归合并其他部分并统计。
相关文章:

归并排序——逆序数对的统计
逆序数对的统计 题目描述 运行代码 #include <iostream> using namespace std; #define LL long long const int N 1e5 5; int a[N], tmp[N]; LL merge_sort(int q[], int l, int r) {if (l > r)return 0; int mid l r >> 1; LL res merge_sort(q, l,…...
)
基于截图和模拟点击的自动化压测工具开发(MFC)
1.背景 想对一个MFC程序做自动压测功能,根据判断程序界面某块区域是否达到预定状态,来自动执行鼠标点击或者键盘输入的操作,以解决测试人员需要重复手动压测问题。 1.涉及的技术 串口控制,基于MFC橡皮筋类(CRectTracker)做一个…...

力扣每日一题 6/10
881.救生艇[中等] 题目: 给定数组 people 。people[i]表示第 i 个人的体重 ,船的数量不限,每艘船可以承载的最大重量为 limit。 每艘船最多可同时载两人,但条件是这些人的重量之和最多为 limit。 返回 承载所有人所需的最小船…...

[知识点] 内存顺序属性的用途和行为
C标准库中定义了以下几种内存顺序属性: std::memory_order_relaxedstd::memory_order_consumestd::memory_order_acquirestd::memory_order_releasestd::memory_order_acq_relstd::memory_order_seq_cst 1. std::memory_order_relaxed 定义:不提供同步…...
索引的创建和优化)
JAVA Mongodb 深入学习(二)索引的创建和优化
一、常用索引类型 1、单个索引 单个索引的创建 db.你的表名.createIndex({"你的字段名":1}) 单个索引的创建且是唯一索引 db.你的表名.createIndex({"你的字段名":1}),{ unique: true }) 2、复合索引 将多个过滤的字段,做成索引,…...

转让北京劳务分包地基基础施工资质条件和流程
地基基础资质转让流程是怎样的?对于企业来说,资质证书不仅是实力的证明,更是获得工程承包的前提。而在有了资质证书后,企业才可以安心的准备工程投标,进而在工程竣工后获得收益。而对于从事地基基础工程施工的企业,需…...
Python基础——字符串
一、Python的字符串简介 Python中的字符串是一种计算机程序中常用的数据类型【可将字符串看作是一个由字母、数字、符号组成的序列容器】,字符串可以用来表示文本数据。 通常使用一对英文的单引号()或者双引号(")…...

AP的数据库性能到底重要吗?
先说结论:没那么重要。甚至可能不重要。 我用我的经历和分析给大家说说。诸位看看如何。 不重要的观点是不是不能接受? 因为这些是站在我们角度觉得的。而实际上使用者(业务或者用户),真的不太在乎我们所在乎的。 …...
Vue3【二】 VSCode需要安装的Vue语法插件
VSCode需要安装的 适配Vue3的插件 Vue-Official插件安装...
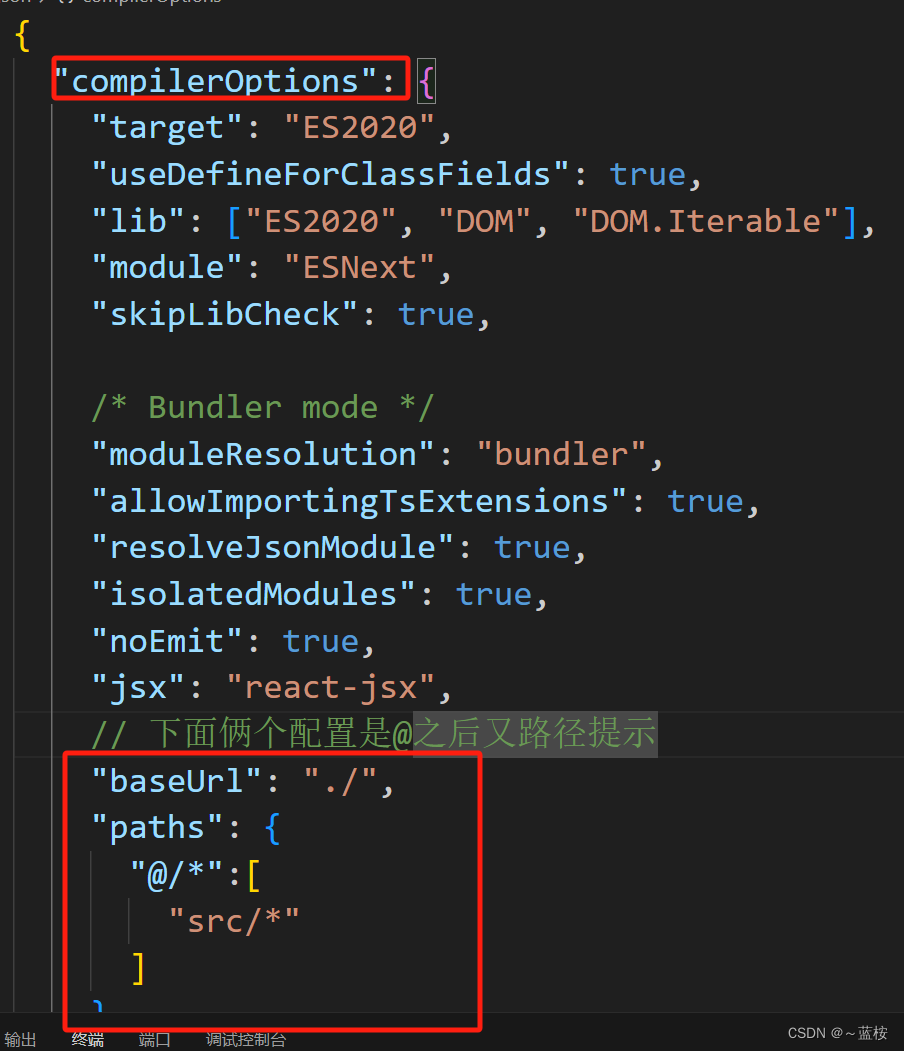
设置路径别名
一、描述 如果想要给路径设置为别名,就是常见的有些项目前面的引入文件通过开头的,也就是替换了一些固定的文件路径,怎么配置。 二、配置 import { defineConfig } from vite import react from vitejs/plugin-react import path from path…...

人事信息管理系统(Java+MySQL)
一、项目背景 在现代企业中,管理大量员工的工作信息、薪资、请假、离职等事务是一项非常繁琐和复杂的任务。传统的手工管理方式不仅效率低下,而且容易出错。为了提高人事管理的效率,减少人工操作带来的错误,企业迫切需要一个高效…...

Python 中生成器与普通函数的区别
在Python中,生成器和普通函数有一些区别。 生成器使用 yield 语句从函数中返回一个值,而不是使用 return 语句。当生成器函数被调用时,它会返回一个迭代器对象,而非立即执行函数体内的代码。 生成器函数可以通过多次调用 yield 语…...
最小栈、栈的弹出(C++)
1.最小栈 思路分析: 代码: class MinStack { public:MinStack() {}void push(int val) {st.push(val);//两种情况需要更新最小值//1.最小栈为空(就是存最小值的那个栈)//2.插入的值小于或等于最小栈的栈顶元素if(minstack.empty()||minstack.top()>…...
20240607每日通信--------VUE3前端引入scoket-io,后端引入Netty-SocketIO,我成功了,希望一起交流沟通
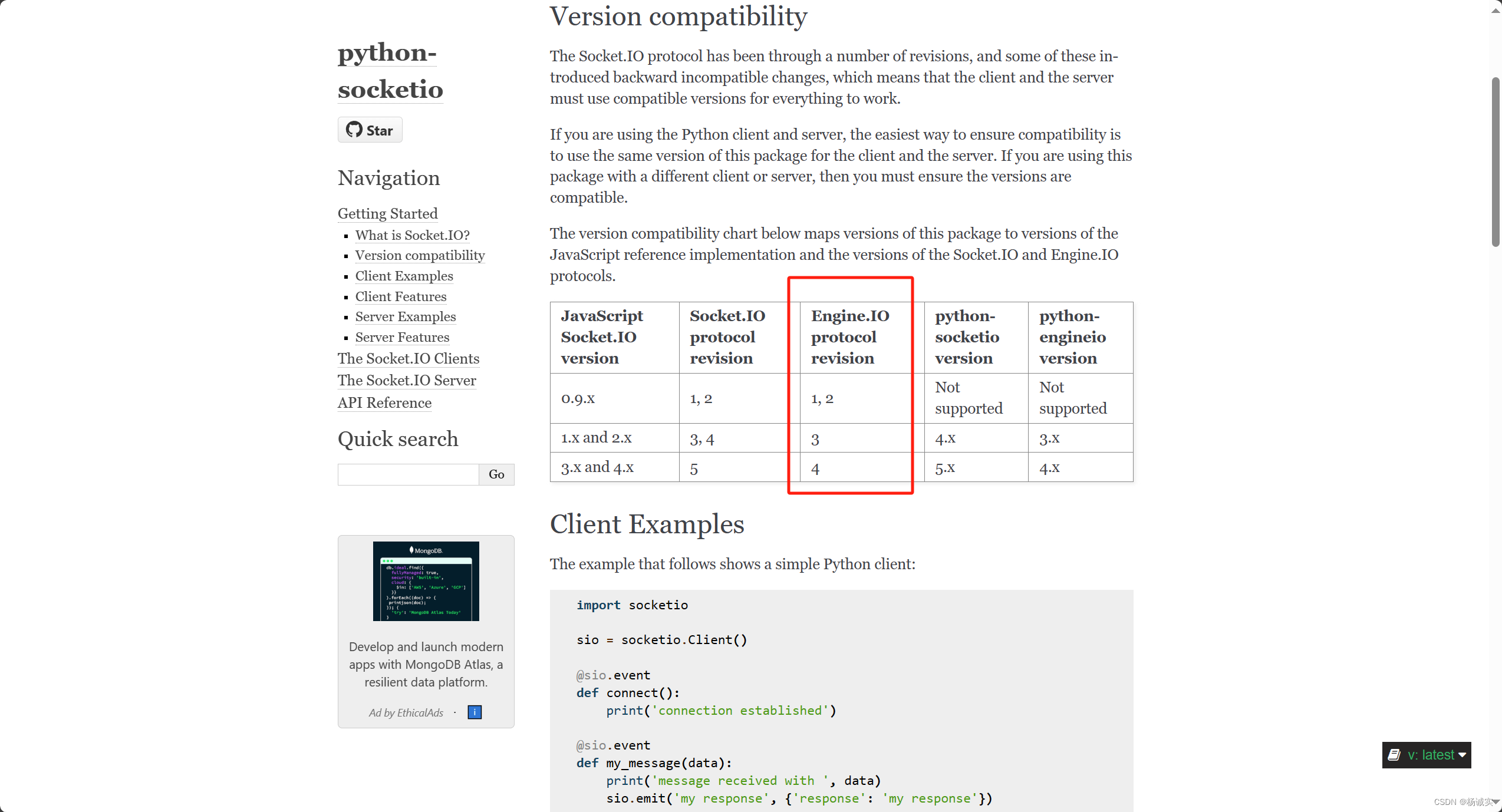
无语 前置: VUE3 前端集成scoket-io socket.io-client Sringboot 3.0JDK17集成Netty-SocketIO Netty-SocketIO 失败原因一: 前期决定要写demo时候,单独了解了,后端引入Netty-SocketIO注意事项,详见我先头写的博客 前…...
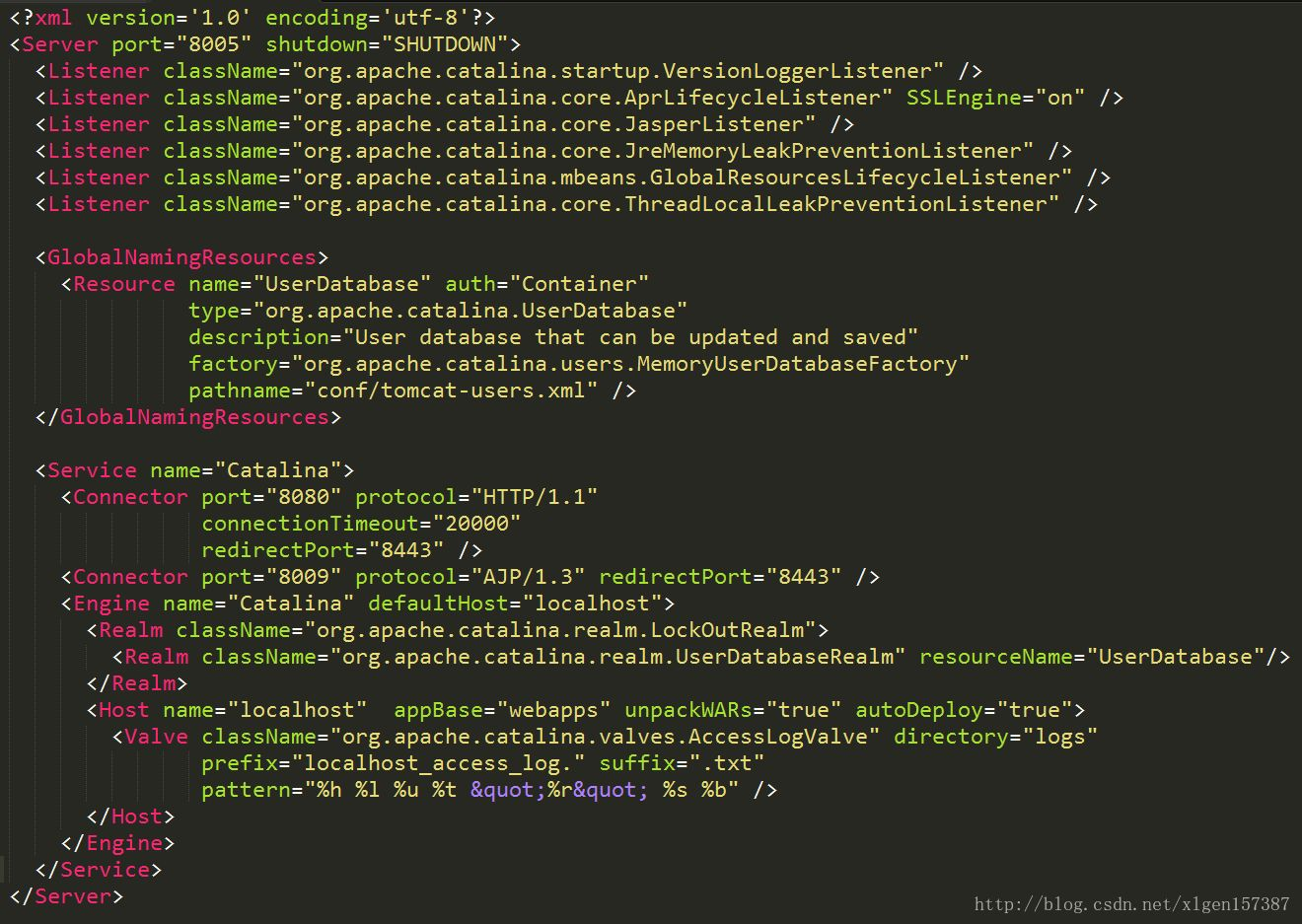
Tomcat源码解析(八):一个请求的执行流程(附Tomcat整体总结)
Tomcat源码系列文章 Tomcat源码解析(一):Tomcat整体架构 Tomcat源码解析(二):Bootstrap和Catalina Tomcat源码解析(三):LifeCycle生命周期管理 Tomcat源码解析(四):StandardServer和StandardService Tomcat源码解析(五)&…...

python使用gdb进行堆栈查看与调试
以ubuntu示例,先安装gdb与python-dbg,dbg按照python版本安装 apt install -y gdb python3.10-dbg 使用top查看python进程,使用gdb操作python进程 gdb python3 6618 加载环境 source /usr/share/gdb/auto-load/usr/bin/python3.10-gdb.py…...

【DevOps】路由与路由器详细介绍:原理、功能、类型及应用场景
目录 一、路由详细介绍 1、什么是路由? 2、路由的基本原理 3、 路由协议 静态路由 动态路由 4、 路由表 5、 路由算法 6、路由的优缺点 优点 缺点 7、 路由应用场景 二、路由器详细介绍 1、什么是路由器? 2、 路由器的工作原理 3、路由器…...

【WP|9】深入解析WordPress [add_shortcode]函数
add_shortcode 是 WordPress 中一个非常强大的函数,用于创建自定义的短代码(shortcodes)。短代码是一种简洁的方式,允许用户在内容中插入动态的、可重用的功能。通过 add_shortcode,开发者可以定义自己的短代码&#x…...

Qt QStackedWidget类详细分析
一.定义 QStackedWidget类是一个容器控件,它提供了一个堆叠的页面布局方式,每个页面可以包含一个子部件。在QStackedWidget中,只有当前活动的页面是可见的,其他页面会被隐藏起来。 QStackedWidget类的常用方法包括: a…...
)
Java数据结构与算法(leetcode热题881. 救生艇)
前言 救生艇属于贪心算法,解题之前条件一定要归纳好。题目中存在3个要求: 1.一艘船最多坐2人 2.船数要求最小 3.每艘船重量小于limit 意味着体重较轻的两人可以同乘一艘救生艇。 . - 力扣(LeetCode) 实现原理 1.重量大的有…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...
