R语言探索与分析18-基于时间序列的汇率预测
一、研究背景与意义
汇率是指两个国家之间的货币兑换比率,而且在国家与国家的经济交流有着举足轻重的作用。随着经济全球化的不断深入,在整个全球经济体中,汇率还是一个评估国家与国家之间的经济状况和发展水平的一个风向标。汇率的变动会对一个国家的对外贸易频繁度、外汇储备以及对于国内的物价水平都会产生一定的影响。故针对于汇率的变动,应该采取相应的措施及政策。....
二、国内外研究现状及总结
随着我国经济的不断发展进步,人民币在国际上的地位逐渐提升,出现了大批学者对于汇率的研究,其研究的角度有许多,其中具有代表性的有:研究影响汇率波动的因素、关于汇率政策与制度的研究以及通过建立适当的模型来进行汇率波动的研究和预测,个人看来,其中最为主流的角度还是建立相应的模型来进行研究。.....
三、研究对象
本文的研究对象是2009年至2020年的中美的月度汇率数据,数据来源于雅虎财经网,其中包括每月开盘、收盘价,每月最高价最低价以及涨跌幅度。为了分析清晰,本文选择了每月收盘价为主要序列数据。
首先将所获取得到的数据进行清洗、缺失值处理等预处理操作。然后将处理好的数据进行分析,然后选择适当的模型进行预测,最后得出相应的结论。
四、主要研究内容和方法
本文主要是以时间序列分析为主要基础,针对特定时间段内的中美汇率波动来分析建模以及预测后期的汇率走势,重点介绍本论文研究主要运用的ARIMA模型以及ARCH、GARCH模型的理论,然后针对数据来进行实证分析,做出相应的预测。....
五、模型知识概述
略
六、实证分析
本文选取了2009年1月至2020年1月的中美汇率月度数据,其中数据包括每月的开盘价(open),收盘价(close),每月中最高点、最低点数据以及汇率变动比率等等,为了研究的更好进行,本文选择的是每月的收盘价为主要数据来进行分析及操作。
pop<-read.table("D:/网页下载/USD_CNY历史数据.csv",sep=",",header = T)
pop
pirce<-pop$close
HL<-ts(pirce,frequency = 12,start = 2009)
plot(HL,main = "汇率变动",xlab = "年份",ylab="汇率变动量")
#白噪声检验
for(i in 1:2) print(Box.test(HL,type = "Ljung-Box",lag=6*i))
随后,对于本文的时序数据进行描述性统计,其具体结果如下表:
表 时序数据描述性统计
| Min | 1st Qu | Median | Mean | 3rd Qu | Max |
| 6.054 | 6.284 | 6.584 | 6.562 | 6.827 | 7.154 |
其次,进行纯随机性检验,只有当序列为非白噪声序列,才能进行后续操作,否则是无意义的。
表 纯随机性检验
| Box-Ljung test | ||
| Data: 2009年1月-2020年1月 | ||
| X-squared = 664.74 | df=6 | P_value<2.2e-16 |
| X-squared = 1029.8 | Df=12 | P_value<2.2e-16 |

从图分析,中美的月度汇率的时间序列图形在2009年-2020波动起伏较大,可见受许多政治、经济等因素的影响,单从时序图可以判断,该序列是属于非平稳序列
为了保证其科学性,下一步需要做关于该序列的ADF单根检验。
表 中美汇率的ADF检验
| Augmented Dickey-Fuller Test | ||
| Alternative : stationary | ||
| Type 1:no drift no trend | ||
| Lag: | ADF | P_value |
| 0 | -0.454 | 0.513 |
| 1 | -0.396 | 0.530 |
| 2 | -0.384 | 0.533 |
| 3 | -0.372 | 0.537 |
| 4 | 0.378 | 0.535 |
| Type 2: with drift no trend | ||
| 0 | -1.49 | 0.526 |
| 1 | -1.95 | 0.347 |
| 2 | -1.93 | 0.356 |
| 3 | -2.08 | 0.296 |
| 4 | -1.93 | 0.354 |
| Type 2: with drift with trend | ||
| 0 | -1.71 | 0.696 |
| 1 | -2.16 | 0.504 |
| 2 | -2.15 | 0.510 |
| 3 | -2.29 | 0.452 |
| 4 | -2.19 | 0.493 |
从上表可以看出,其P值大于0.05的显著性水平,故在0.05的显著性水平下,接受其原假设,即表明该序列为非平稳序列。
从上表3.3可以看出,其P值大于0.05的显著性水平,故在0.05的显著性水平下,接受其原假设,即表明该序列为非平稳序列。
#打印出关于季节性趋势的图表
dc<-decompose(HL)
season<-dc$figure
plot(season,type = "b",xaxt="n",xlab = "Month",ylab = "Season Effect")

由于本文数据为汇率数据,该类型数据通常具有集聚效应,故在序列为平稳序列基础上,查看其差分之后差分图。
#差分和画出差分图
diff(HL)
plot(diff(HL))win.graph(width=3.25,height=2.5,pointsize=8)
tsdisplay(diff(HL))
dc<-decompose(diff(HL))
plot(dc)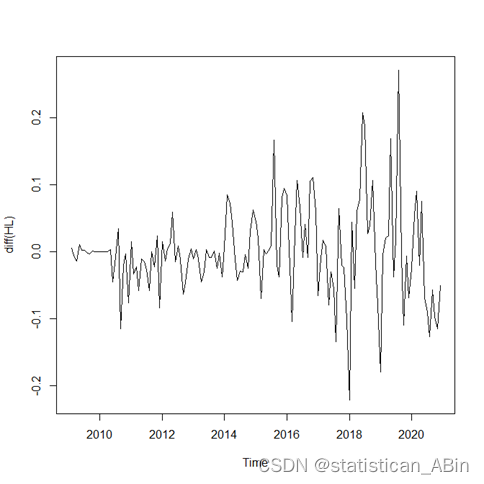
模型选择
#ARIMA(1,1,)
model=Arima(HL,order=c(1,1,0))
summary(model)#aic = -2588.36| Training set error measures: | |||||||||||
| Series: 中美汇率 | |||||||||||
| ARIMA(0,1,1) | |||||||||||
| Coefficients: | |||||||||||
| ma1 | |||||||||||
| 0.3127 | |||||||||||
| s.e. | 0.0811 | ||||||||||
| Sigma^2=0.004074: | Log likelihood =191.02 | ||||||||||
| AIC=-378.04 | AICc=-377.95 | BIC=-372.11 | |||||||||
| ME | RMASE | MAE | MPE | MAPE | MASE | ACF1 | |||||
| Training set | -0.0016 | 0.0634 | 0.0447 | -0.0260 | -0.6762 | 0.2001 | 0.0067 | ||||
无论是AIC准则还是BIC准则,模型都定位一个模型,即ARIMA(0,1,1)。并且也可从表中得出模型的各个评判指标。最终模型的表达式应为:

接下来进行残差分析
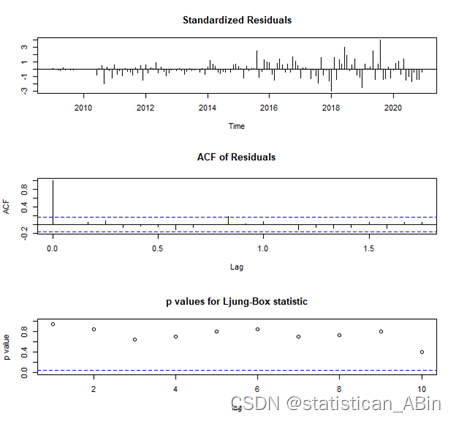
接下来GARCH检验及预测看是否存在ARCH效应。
| ARCH LM-test ; null hypothesis: no ARCH effects | ||
| Data: model$residual | ||
| Chi-squared=2.9169 | df=1 | P_value=0.08766 |
| Chi-squared=3.0018 | df=2 | P_value=0.0229 |
| Chi-squared=9.0705 | df=3 | P_value=0.02837 |
| Chi-squared=10.198 | df=4 | P_value=0.03722 |
| Chi-squared=12.263 | df=5 | P_value=0.03136 |
进一步,运用所得到的模型进行预测,本文由于是月度数据,所以为了保证预测的准确性,将预测阶数定为5阶,其最终预测结果如下图和表。
###模型预测
model=Arima((HL),order=c(0,1,1),include.mean = T,transform.pars=T)
model
#预测未来5期,99.5%置信区间
forecast<-forecast(model,h=5,levels=c(95.5))
forecast
##可视化预测图
plot(forecast)
七、结论与展望
本文通过分析2009年1月至2020年1月的中美汇率,首先通过差分,将序列变为平稳序列,再通过季节因素提取,提取出其他因素,然后进行ARCH检验(本文是LM检验),最后建立模型ARCH(1,1)和ARIMA(0,1,1)进行分析和预测,最终预测结果表现为中美汇率的整体趋势是往下波动。但是随着时间周期的变成,预测误差变得越来越大,这可能是传统预测模型的缺陷所在.....
代码和数据
代码和完整报告
创作不易,希望大家多多点赞收藏和评论!
相关文章:

R语言探索与分析18-基于时间序列的汇率预测
一、研究背景与意义 汇率是指两个国家之间的货币兑换比率,而且在国家与国家的经济交流有着举足轻重的作用。随着经济全球化的不断深入,在整个全球经济体中,汇率还是一个评估国家与国家之间的经济状况和发展水平的一个风向标。汇率的变动会对…...

30岁迷茫?AI赛道,人生新起点
前言 30岁,对于许多人来说,是一个人生的分水岭。在这个年纪,有些人可能已经在某个领域取得了不小的成就,而有些人则可能开始对未来的职业方向感到迷茫。如果你正处于这个阶段,那么你可能会问自己:30岁转行…...

开门预警系统技术规范(简化版)
开门预警系统技术规范(简化版) 1 系统概述2 预警区域3 预警目标4 功能需求5 功能条件6 显示需求7 指标需求1 系统概述 开门预警系统(DOW),在自车停止开门过程中,安装在车辆的传感器(如安装在车辆后保险杆两个角雷达)检测从自车后方接近的目标车(汽车、摩托车等)的相对…...

Django与MySQL:配置数据库的详细步骤
文章目录 Django-MySQL 配置配置完执行数据迁移,如果报错: Error loading MySQLdb module, Django-MySQL 配置 # settings.pyDATABASES {# 默认配置sqlite3数据库# default: {# ENGINE: django.db.backends.sqlite3,# NAME: BASE_DIR / db.sqli…...

GPT-4o short description
GPT-4o,作为OpenAI最新推出的人工智能模型,无疑在人工智能领域掀起了新的波澜。 一、版本间的对比分析 与前一版本GPT-4相比,GPT-4o在多个方面进行了显著的改进和优化。首先,在参数规模上,GPT-4o达到了2000亿个参数&…...

MATLAB 矩阵
创建矩阵直接输入:使用 zeros, ones, eye 函数:使用 rand, randi 函数:使用 diag 函数: 矩阵操作矩阵加法和减法:矩阵乘法:矩阵转置:矩阵求逆:矩阵分解:矩阵大小…...

LED灯的功率以及好的品牌推荐
LED灯的功率选择主要根据使用场景、照明需求以及灯具类型来决定。常见的LED灯功率范围在0.5W到100W之间,不同的功率范围适用于不同的场景。 对于小型照明设备,如小夜灯或手电筒,通常选择0.5W到3W的LED灯,足以满足基本的照明需求。…...
Linux “ 软件管理 “
软件管理 widows 安装 方法一: 双击exe安装包,就可以安装。 用exe安装的软件会破记录到注册表中。 注册会记录安装位置,软件名称。 方法二: 用绿色方式进行安装。 不用写到注册表中,因此无法在开始菜单里面查看和卸…...

【uni-app】申请高德地图key,封装map.js,实现H5、iOS、Android通过getlocation获取地图定位信息
文章目录 map组件基础使用封装map.js,实现定位1、使用第三方地图:高德,申请对应平台key1、申请H5 key2、申请微信小程序 key3、申请android key查看证书详情,可以看到SHA1查看/设置Android包名 4、申请ios key 2、封装map1、lib/m…...

使用rufus做Kali Linux时持久分区大小如何设置
持久分区大小是什么意思: 持久分区大小指的是在U盘安装引导Kali Linux时,为保存Kali修改后的设置(如中文界面显示等)而预留的空间大小。这个空间相当于电脑中的D盘,用于保存修改后的设置。 而剩下的空间则用于安装Kali…...

Java高阶数据结构-----并查集(详解)
目录 🧐一.并查集的基本概念&实例: 🤪二.并查集代码: 😂三:并查集的一些习题: A.省份数量 B.等式方程的可满足性 🧐一.并查集的基本概念&实例: 并查集概念&…...
GitLab教程(三):多人合作场景下如何pull代码和处理冲突
文章目录 1.拉取别人同步的代码到本地的流程2.push冲突发生场景情景模拟简单的解决方法 在这一章中,为了模拟多人合作的场景,我需要一个人分饰两角。 执行git clone xx远端仓库地址 xx文件夹命令,在clone代码时指定本地仓库的文件夹名&#…...

模版偏特化之std::enable_if
1 SFINAE。 2 条件特化。可用作额外的函数参数(不可应用于运算符重载)、返回类型(不可应用于构造函数与析构函数),或类模板或函数模板形参。 函数参数: #include <iostream> #include <type_tra…...

好用的Web数据库管理工具推荐(ChatGPT的推荐)
在现代数据管理和开发中,Web数据库管理工具变得越来越重要。这些工具不仅提供了直观的用户界面,还支持跨平台操作,方便用户在任何地方进行数据库管理。 目录 1. SQLynx 2. phpMyAdmin 3. Adminer 4. DBeaver 5 结论 以下是几款推荐的Web…...
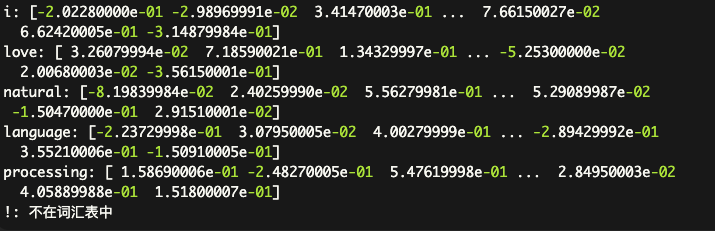
encoding Token和embedding 傻傻分不清楚?
encoding 编码 “encoding” 是一个在计算机科学和人工智能领域广泛使用的术语,它可以指代多种不同的过程和方法。核心就是编码:用某些数字来表示特定的信息。当然你或许会说字符集(Unicode)更理解这种概念,编码更强调这种动态的过程。而字符…...
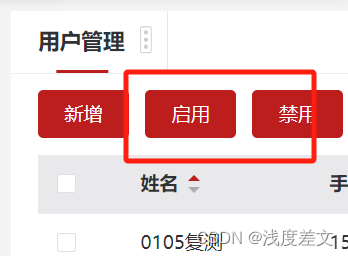
一个公用的数据状态修改组件
灵感来自于一项重复的工作,下图中,这类禁用启用、审核通过不通过、设计成是什么状态否什么状态的场景很多。每一个都需要单独提供接口。重复工作还蛮大的。于是,基于该组件类捕获组件跳转写了这款通用接口。省时省力。 代码如下:…...

[python]yfinance国内不能使用
yfinance国内不能使用,可以使用tushare、akshare代替 import yfinance as yf# 输入股票代码 stock_symbol AAPL # 替换为你想要查询的股票代码# 获取股票数据 data yf.download(stock_symbol)# 打印实时数据 print(data) pip install akshare import akshare …...
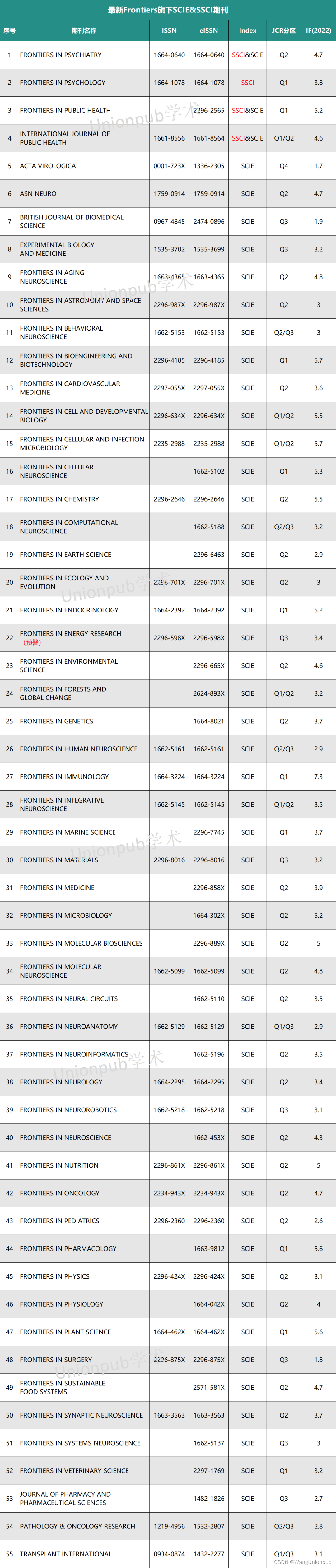
Frontiers旗下期刊,23年分区表整理出炉!它还值得投吗?
本周投稿推荐 SSCI • 中科院2区,6.0-7.0(录用友好) EI • 各领域沾边均可(2天录用) CNKI • 7天录用-检索(急录友好) SCI&EI • 4区生物医学类,0.5-1.0(录用…...

基于JSP的毕业生就业信息管理系统
开头语: 你好,我是专注于信息系统开发的学长猫哥。如果您对毕业生就业信息管理或相关技术感兴趣,欢迎联系我交流。 开发语言: JSP 数据库: MySQL 技术: JSP技术 SSM框架 工具: Eclips…...

CDN、CNAME、DNS
CDN、CNAME、DNS 域名解析是将域名转换为IP地址的过程。当用户在浏览器中输入域名时,计算机需要在DNS系统中找到对应的IP地址,以便能够访问该网站。 CDN(Content Delivery Network,内容分发网络)是一种用于加速网站访…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
