【数据结构】二叉树：一场关于节点与遍历的艺术之旅

专栏引入

哈喽大家好，我是野生的编程萌新，首先感谢大家的观看。数据结构的学习者大多有这样的想法：数据结构很重要，一定要学好，但数据结构比较抽象，有些算法理解起来很困难，学的很累。我想让大家知道的是：数据结构非常有趣，很多算法是智慧的结晶，我希望大家在学习数据结构的过程是一种愉悦的心情感受。因此我开创了《数据结构》专栏，在这里我将把数据结构内容以有趣易懂的方式展现给大家。

1.二叉树的链式存储结构 

前面我们说过顺序存储结构一般只适用于完全二叉树，既然顺序存储适应性不强，我们既要考虑链式存储结构了。二叉树每个节点最多有两个孩子，所以为它设计一个数据域和两个指针域是比较自然的想法 ，我们称这样的链表为二叉链表。节点结构图如下所示：

其中，data是数据域，leftchild和rightchild都是指针域，分别存放指向左孩子和右孩子的指针，下面是二叉链表的节点结构定义代码：

typedef struct BinaryTreeNode
{TDataType data;struct TreeNode* leftchild;struct TreeNode* rightchild;
}BTNode;

 结构示意图如下：

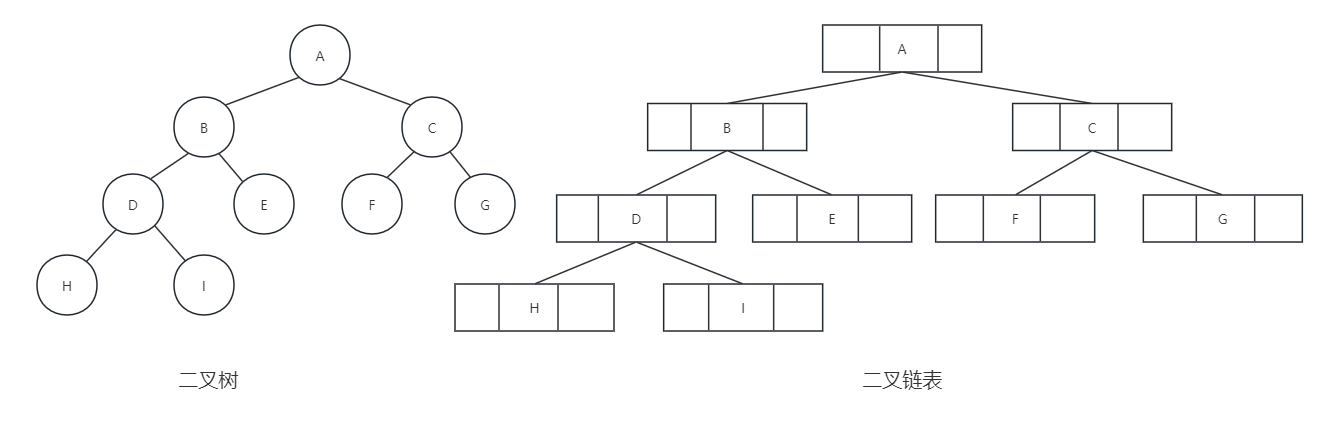
就如同我们在树的存储结构中讨论的一样，如果有需要，还可以增加一个指针指向其双亲的指针域，那样就称之为三叉链表，后续在红黑树时会提到，这里就不细讲了。 

2.二叉树的遍历

 二叉树的遍历是指从根节点出发，按照某种次序依次访问二叉树中的所有节点，使得每一个节点被访问一次且仅被访问一次。这里有两个关键词：访问和次序。访问其实是根据实际需要来确定具体做什么，比如：对某个节点进行相关计算、输出打印等。二叉树的遍历次序不同于线性结构，最多也就是从头到尾、循环、双向等简单的遍历方式。树的节点之间不存在唯一的前驱和后继关系，在访问一个节点后，下一个访问的节点面临着不同的选择。就像我们高考填报志愿要面临着去哪个城市、哪所大学、具体专业等选择，由于选择的方式不同，遍历的次序就完全不同了。

二叉树的遍历方式可以有很多种，如果我们限制了从左到右的习惯方式，那么主要就分为四种：前序遍历、中序遍历、后序遍历、层序遍历。

2.1前序遍历

二叉树的前序遍历规则是：若二叉树为空，则空操作返回，否则先访问根节点，然后前序遍历左子树，再前序遍历右子树。即按照“根节点-左子树-右子树”的顺序遍历二叉树。像下面这张图中的二叉树，遍历顺序是ABDECFG:

二叉树的定义是用递归的方式，所以，实现遍历也可以采用递归，而且极其简洁明了，我们先来看看二叉树的前序遍历，具体代码如下：

void PreOrderTraverse(BiTree T)
{if(T==null)return;printf("%c",T->data);PreOrderTraverse(T->lchild);preOrderTraverse(T->rchild);
}

假设我们有如下图这样的一棵二叉树T，这棵树已经用二叉链表结构存储在内存当中:

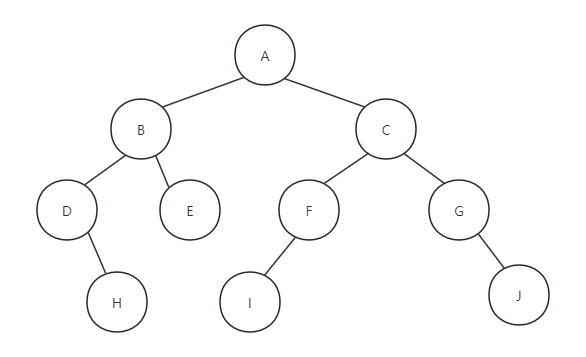
当我们调用PreOrderTraverse(T)函数时，我们来看看程序是怎么运行的：

（1）当调用PreOrderTraverse(T)时，根节点不为NULL，所以执行printf，打印字母A，就像下面这样：

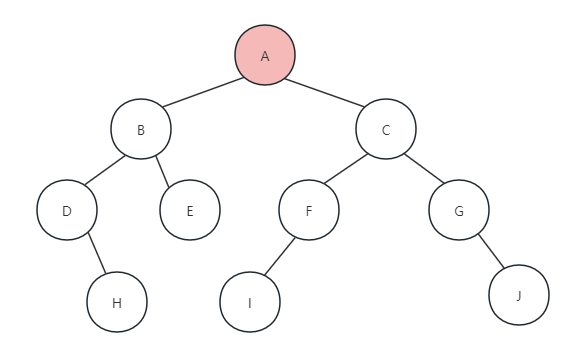
（2）接着我们调用PreOrderTraverse(T->lchild)函数，访问根节点A的左孩子，不为NULL，执行printf打印字母B，如下图所示：

 

（3）此时再次递归调用PreOrderTraverse(T->lchild)函数，来访问B节点的左孩子，执行printf函数打印字母D，如下图所示：

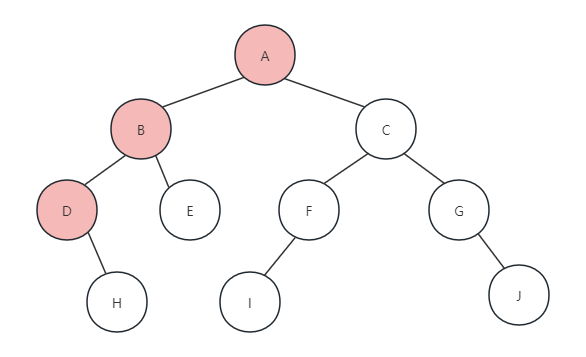
 （4）再次递归调用PreOrderTraverse(T->rchild)，访问D节点的左孩子，此时因为D节点没有左孩子，所以T=NULL，返回此函数，此时递归调用PreOrderTraverse(T->rchild)，访问D节点的右孩子，执行printf打印H，如下图所示：

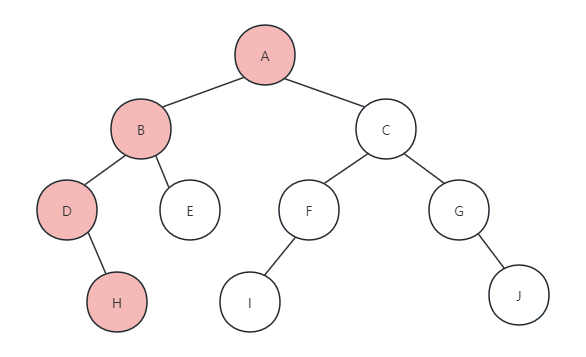
（5） 再次递归调用PreOrderTraverse(T->lchild)，访问H节点的左孩子，H节点没有左孩子，返回，调用PreOrderTraverse(T->rchild)，访问H节点的右孩子，也是NULL，返回。于是，此函数执行完毕，返回到上一级递归的函数（即打印D节点的函数），也执行完毕，返回打印D节点时的函数，调用PreOrderTraverse(T->rchild)，找到E节点，打印字母E，如下图所示：

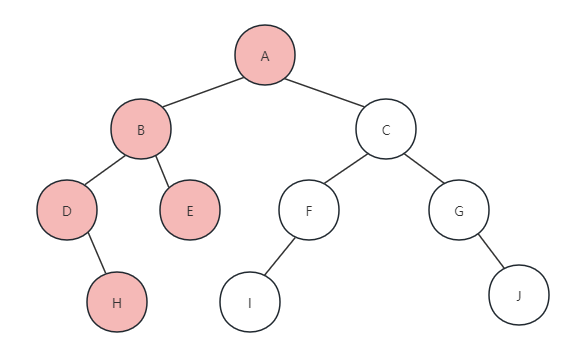
（6）由于节点E没有左右孩子，返回打印B节点的递归函数，递归执行完毕，返回到最初的PreOrderTraverse，调用PreOrderTraverse(T->rchild)，访问A节点的右孩子，如图所示：

 

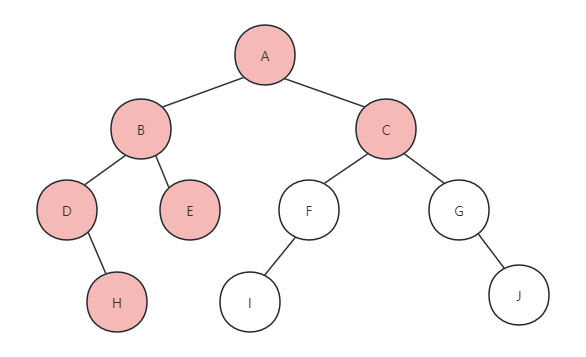
（7）之后类似前面的递归调用，一依次打印F、I、G、J，这里步骤就省略喽。

 综上所述，前序遍历这棵二叉树的节点的顺序是ABDHECFIGJ。 

2.2中序遍历 

规则是若树为空，则空操作返回，否则从根节点开始（注意不是先访问根节点），中序遍历是遍历根节点的左子树，然后是访问根节点，最后中序遍历右子树，即按照“左子树-根节点-右子树”的顺序遍历二叉树。如下图所示的二叉树遍历的顺序为DBEAFCG：

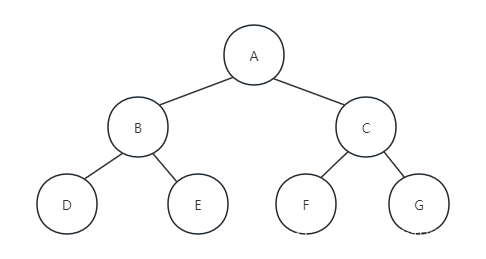
二叉树的中序遍历如何实现呢？别以为很复杂，它和前序遍历其实就是代码顺序上的差异：

void InOrderPraverse(BiTree T)
{if(T==NULL)return;InOrderPraverse(T->lchild);printf("%c",T->data);InOrderPraverse(T->rchild);
}

 换句话说，它等于把调用左孩子的递归函数提前了，就这么简单，我们来看看调用InOrderPraverse(T)函数时，程序是如何运行的呢？

（1）调用PreOrderTraverse(T)，T的根节点不为NULL，于是调用PreOrderTraverse(T->lchild)，访问B节点，当前指针仍不为NULL，继续调用PreOrderTraverse(T->lchild)，访问节点D，继续调用PreOrderTraverse(T->lchild)，访问D节点的左孩子，发现当前指针为NULL，于是返回，打印当前节点D，如下图所示：

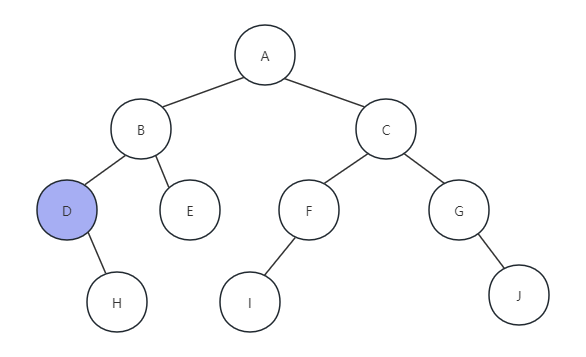
（2）然后调用PreOrderTraverse(T->rchild)，访问节点D的右孩子H，因为H也没有左孩子，所i打印H，如下图所示：

 

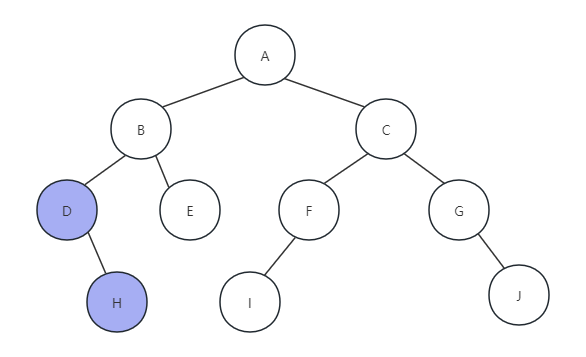
（3） 因为H节点没有右孩子，所以返回，打印节点D函数执行完毕，返回打印字母B，如下图所示：

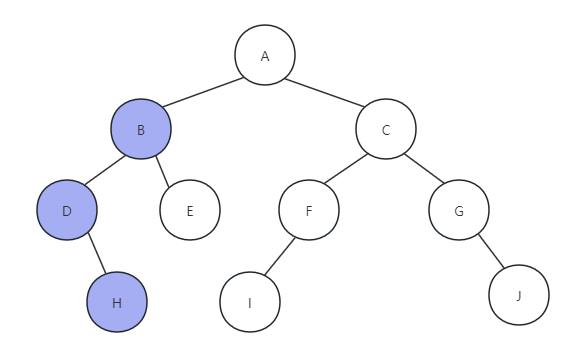
（4）调用PreOrderTraverse(T->rchild)，访问B节点的右孩子，因为E节点没有左孩子，所以打印字母E，如下图所示：

 

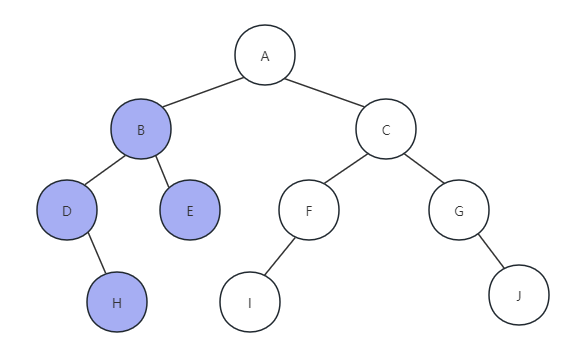
（5）E节点没有右孩子，返回，节点B的递归函数执行完毕，返回到我们最初调用InOrderPraverse的地方，打印字母A，如下图所示：

 

（6）再调用PreOrderTraverse(T->rchild)，访问A节点的右孩子C，再递归访问C节点的左孩子F，接着访问节点F的左孩子I，因为I没有左孩子，打印I，之后分别打印F、C、G、J。这里具体步骤也就省略了。

综上所述，中序遍历这棵二叉树的节点顺序为：D、H、B、E、S、A、I、F、C、G、J。

2.3后序遍历

规则是若树为空，则空操作返回，否则从左到右先叶子后节点地方式遍历访问左右子树，最后访问根节点，即按照“左子树-右子树-根节点”的顺序遍历二叉树。如下图所展示的二叉树，遍历的顺序为DEBFCGA：

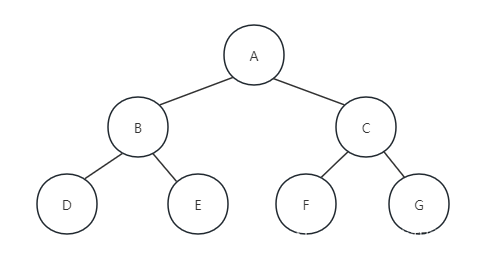
同样地，后序遍历也就很容易想到应该如何写代码了：

void PostOrderPraverse(BiTree T)
{if(T==NULL)return;PostOrderPraverse(T->lchild);PostOrderPraverse(T->rchild);printf("%c",T->data);
}

 如下图所示，后序遍历是先递归左子树，由根节点A->B->D，节点D没有左孩子，再查看节点H，因为节点H没有左右孩子，所以打印字母H，返回

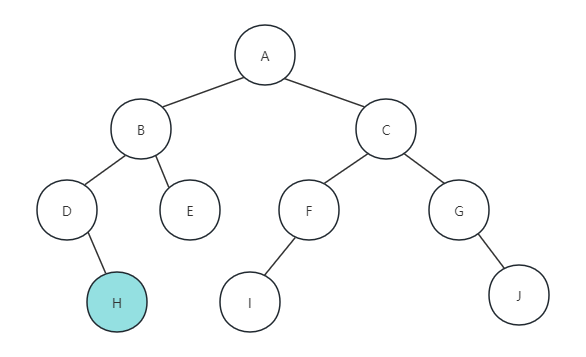
 最终，后序遍历地节点的顺序为H、D、E、B、I、F、J、G、C、A，可以完全参考前面的两个遍历方法来得到这个结果。

2.4层序遍历

规则是若树为空，则空操作返回，否则从树的第一层，也就是从根节点开始访问，从上而下逐层遍历，在同一层中，按从左到右地顺序对节点逐个访问。如下图所示：遍历地顺序为ABCDEFG。

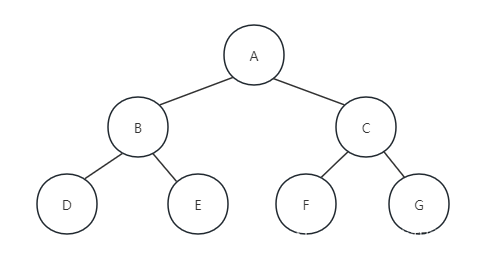
2.5推到遍历的结果 

 有一种题目为了考察我们对二叉树遍历的掌握程度，是这样出题的：已知一棵二叉树的前序遍历序列为ABCDEF，中序遍历序列为CBAEDF，请问这棵二叉树的后序遍历结果是多少？

对于这样的题目，如果真的完全了解了前中后序地原理，是不难滴。三种遍历都是从根节点开始的，前序遍历是先打印再递归左和右。所以前序遍历序列为ABCDEFG，第一个字母是A被打印出来，就说明A是根节点的数据，再由中序遍历序列是CBAEDF，可以知道C和B是A左子树的节点，E、D、F是A右子树的节点，如下图所示：

然后我们看前序中的C和B，他的顺序是ABCDEF，是先打印B后打印C，所以B应该是B地左孩子，而C就只能是B地孩子，此时是左孩子还是右孩子还不确定，再看中序序列是CBAEDF，而C是在B地前面打印，这就说明C是B地左孩子，否则就是右孩子了，如下图所示：

 

再看前序中的E、D、F，它的顺序是ABCDEF，那就意味着D是A节点的右孩子，E和F是D地子孙，注意，他们中其中一个不一定是孩子，有可能是孙子，再来看中序序列是CBAEDF，由E在D地左侧，而F在右侧，所以可以确定E是D的左孩子，F是D的右孩子。因此最终得到的为叉树如下图所示：

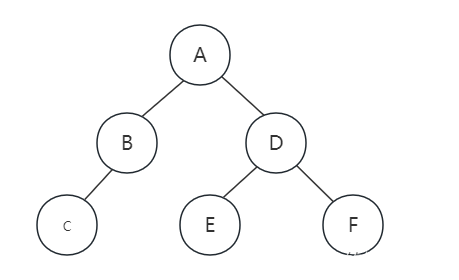
为了避免推到中的失误，最好在心中递归遍历，检查一下这棵树的前序和中序遍历序列是否与题目中的相同，已经恢复了二叉树，要获得他的后序遍历结果就是易如反掌，结果就是CBEFDA。

反过来，如果我们的题目是这样：二叉树的中序序列是ABCDEFG，后序序列是BDCAFGE，求前序序列。

这次简单，由后序的BDCAFGE，得到E是根节点，因此前序首字母是E。于是根据中序序列分为两棵树ABCD和FG，由后序序列的BDCAFGE，知道A是E的左孩子，前序序列目前分析为EA。再由中序序列的ABCDEFG，知道BCD是A节点的右子孙，再由后序序列的BDCAFGE知道C节点是A节点的右孩子，前序序列目前分析得到EAC。由中序序列ABCDEFG，得到B是C的右孩子，所以前序序列目前分析为EACBD，由后序序列BDCAFGE，得到G是E的右孩子，于是F就是G的孩子，而且还是左孩子，前序遍历序列的最终结果就是EACBDGF。

从这里我们也得到了两个二叉树遍历的性质：

1. 已知前序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。
2. 已知后序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。

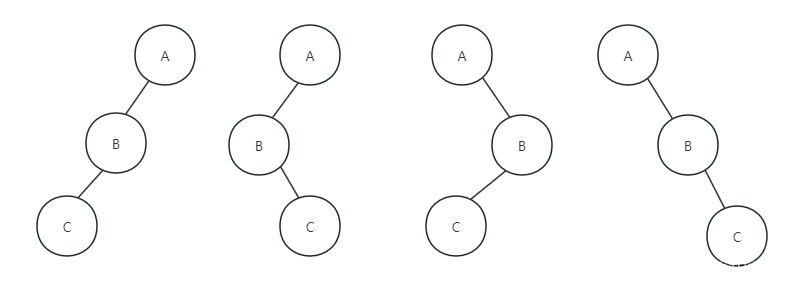
但是要注意了，已知前序和后序遍历，是不能确定一棵二叉树的，原因也很简单，比如前序序列是ABC，后序序列是CBA，我们可以确定A一定是根节点，但接下来，我们无法知道，哪个节点是左子树，哪个节点是右子树，这棵树可能有如下图所示的四种可能：

3.二叉树的建立 

说了半天，我们该如何在内存中生成一棵二叉链表的二叉树呢？如果我们要在内存中建立一个左下角这样的树，为了能让每个节点确认是否存在有左右孩子，我们对它进行了拓展，变成右下角的样子，也就是将二叉树中的每个结点的空指针引出一个虚结点，其值为一特定值，比如“#”。我们称这种处理后的二叉树为原二叉树的扩展二叉树。扩展二叉树就可以做到一个遍历序列确定一棵二叉树，比如左下角的前序遍历序列为AB#D##C##。 

有了这样的准备，我们就可以把刚才前序遍历的序列AB#D##C##用键盘挨个输入，实现代码如下：

void CreateBiTree(BiTree* T)
{TDataType ch;scanf("%c",&ch);ch=str[index++];if(ch=='#')*T=NULL;else{*T=(BiTree)malloc(sizeof(BiTree));if(!*T)exit(-1);(*T)->data=ch;CreateBiTree(&(*T)->lchild);CreateBiTree(&(*T)->rchild);}
}