【数据结构】排序(直接插入、折半插入、希尔排序、快排、冒泡、选择、堆排序、归并排序、基数排序)
目录
- 排序
- 一、插入排序
- 1.直接插入排序
- 2.折半插入排序
- 3.希尔排序
- 二、交换排序
- 1.快速排序
- 2.冒泡排序
- 三、选择排序
- 1. 简单选择排序
- 2. 堆排序
- 3. 树排序
- 四、归并排序(2-路归并排序)
- 五、基数排序
- 1. 桶排序(适合元素关键字值集合并不大)
- 2. 基数排序
- 基数排序的基本原理
- 基数排序的实现步骤
- 基数排序的代码实现
排序
图片取自博客园 链接: 各种排序算法时间复杂度
1. 排序定义:排序定义——将一个数据元素(或记录)的任意序列,重新排列成一个按关键字有序的序列叫排序(sort)。
按照主关键字排序,排序结果唯一;按照次关键字排序,排序结果可能不唯一。
2. 排序分类:
1.按排序记录所在位置分类:
(1)内部排序:待排序记录存放在内存中;
(2)外部排序:排序过程中需要对外存进行访问的排序;
2.按排序依据分类:
3. 排序所需工作量

4.排序的稳定性
待排序数列中如果有关键字相等的记录,经过某一算法排序后,关键字相等的记录其先后次序始终不变,则这种算法成为稳定的排序算法,具有稳定性。否则不稳定,不具有稳定性。
一、插入排序
插入排序:每次将一个待排序的记录,按关键字的大小插入到已排好序的子序列中的适当位置,直到全部记录插入完毕为止
数据元素类型以及顺序存储结构结构体定义如下:
//数据元素类型
typedef struct{KeyType key; //关键字域//...; //后面就是其它关键字
}ElemType;//数据元素类型//表的顺序存储结构
typedef struct{ElemType r[MAXSIZE+1]; //其中r[0]项为 哨兵项 以便交换的时候 暂存数据int length;//表的长度
}SqList; //顺序存储结构
1.直接插入排序
直接插入排序,待排序的数据用数组和链表存放均可
算法评价:稳定!
时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 最好情况: O ( n ) O(n) O(n)
最好情况:n-1次数据比较,0次数据移动。待排序的数据已经有序。- 平均情况: O ( n 2 ) O(n^2) O(n2)
- 最坏情况: O ( n 2 ) O(n^2) O(n2)
空间复杂度:一个额外的辅助空间 O ( 1 ) O(1) O(1)

//数据元素类型
typedef struct{KeyType key; //关键字域//后面就是其它关键字
}ElemType;//数据元素类型//表的顺序存储结构
typedef struct{ElemType r[MAXSIZE+1]; //其中r[0]项为 哨兵项 以便交换的时候 暂存数据int length;//表的长度
}SqList; //顺序存储结构
算法实现:
void InsertSort(SqList L){int i,j;for(i=2;i<=length;i++){//从第二个到第n个记录依次插入if(L.r[i].key<L.r[i-1].key){L.r[0] = L.r[i];for(j=i-1;L.r[0].key<L.r[j].key;i--){//若r[0]<r[j],则r[j]后移L.r[j+1]=L.r[j];}L.r[j+1]=L.r[0];//将r[0]移至在r[j+1]}}
}2.折半插入排序
待排序的数据元素必须存放于数组
算法评价: 稳定!
时间复杂度: T ( n ) = O ( n 2 ) T(n)=O(n^2) T(n)=O(n2)
空间复杂度: S ( n ) = O ( 1 ) S (n)=O(1) S(n)=O(1)
与直接插入排序相比,查找插入位置方法不同,记录移动次数不变
算法实现:
void BinSrot(SqList &L){int i,j,high,low,mid;for(int i=2;i<=L.length;i++){L.r[0]=L.r[i];low=1;high=i-1;while(low<=high){//折半查找mid=(low+high)/2;if(L.r[0].key<L.r[mid].key)high=mid-1;else low=mid+1;}for(j=i-1;j>=low;j--){L.r[j+1]=L.r[j]; //后移}L.r[low]=L.r[0]; //插入}
}
//(high<low ,查找结束,插入位置为low 或high+1 )
二分插入排序减少了关键字的比较次数,但数据元素的移动次数不变,其时间复杂度与直接插入排序相同。
待排序的数据元素必须存放于数组
算法评价:
时间复杂度: T ( n ) = O ( n 2 ) T(n)=O(n^2) T(n)=O(n2)
空间复杂度: S ( n ) = O ( 1 ) S (n)=O(1) S(n)=O(1)
3.希尔排序
算法评价:不稳定!
时间复杂度: O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
- 最好情况: O ( n l o g n ) O(nlog~n) O(nlog n)
- 平均情况: O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
- 最差情况: O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
空间复杂度: O ( 1 ) O(1) O(1)

先将整个待排序记录分割成若干个子序列分别进行直接插入排序,待整个序列中的记录基本有序时,再对全体记录进行一次直接插入排序。
对待排记录先作“宏观”调整,再作“微观”调整。
增量序列可以有各种取法,但应注意:应使增量序列中的值没有除1的之外的公因子,并且最后一个增量值必须等于1。
希尔排序原理:
//希尔排序void ShellInsert ( SqList &L, int dk ) {//直接插入排序for ( i=dk+1; i<=n; ++i )//if ( L.r[i].key< L.r[i-dk].key) {L.r[0] = L.r[i]; // 暂存在R[0]for (j=i-dk; j>0&&(L.r[0].key<L.r[j].key); j-=dk)L.r[j+dk] = L.r[j]; // 记录后移,查找插入位置L.r[j+dk] = L.r[0]; // 插入} // if
} // ShellInsertvoid ShellSort (SqList &L, int dlta[], int t)
{ // 增量为dlta[]的希尔排序for (k=0; k<t; ++t) //增量ShellInsert(L, dlta[k]);//一趟增量为dlta[k]的插入排序//增量//dlta[k] 怎么取?} // ShellSort二、交换排序
交换排序:两两比较待排序记录的关键值,交换不满足顺序要求的记录,直到全部满足顺序要求为止
//数据元素类型
typedef struct{KeyType key; //关键字域//后面就是其它关键字
}ElemType;//数据元素类型//表的顺序存储结构
typedef struct{ElemType r[MAXSIZE+1]; //其中r[0]项为 哨兵项 以便交换的时候 暂存数据int length;//表的长度
}SqList; //顺序存储结构
1.快速排序
递归!!!
算法评价:不稳定排序
时间复杂度: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 最好情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 平均情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 最差情况: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( l o g 2 n ) − O ( n ) O(log_{2}n)-O(n) O(log2n)−O(n) 认为是 O ( l o g 2 n ) O(log_{2}n) O(log2n)
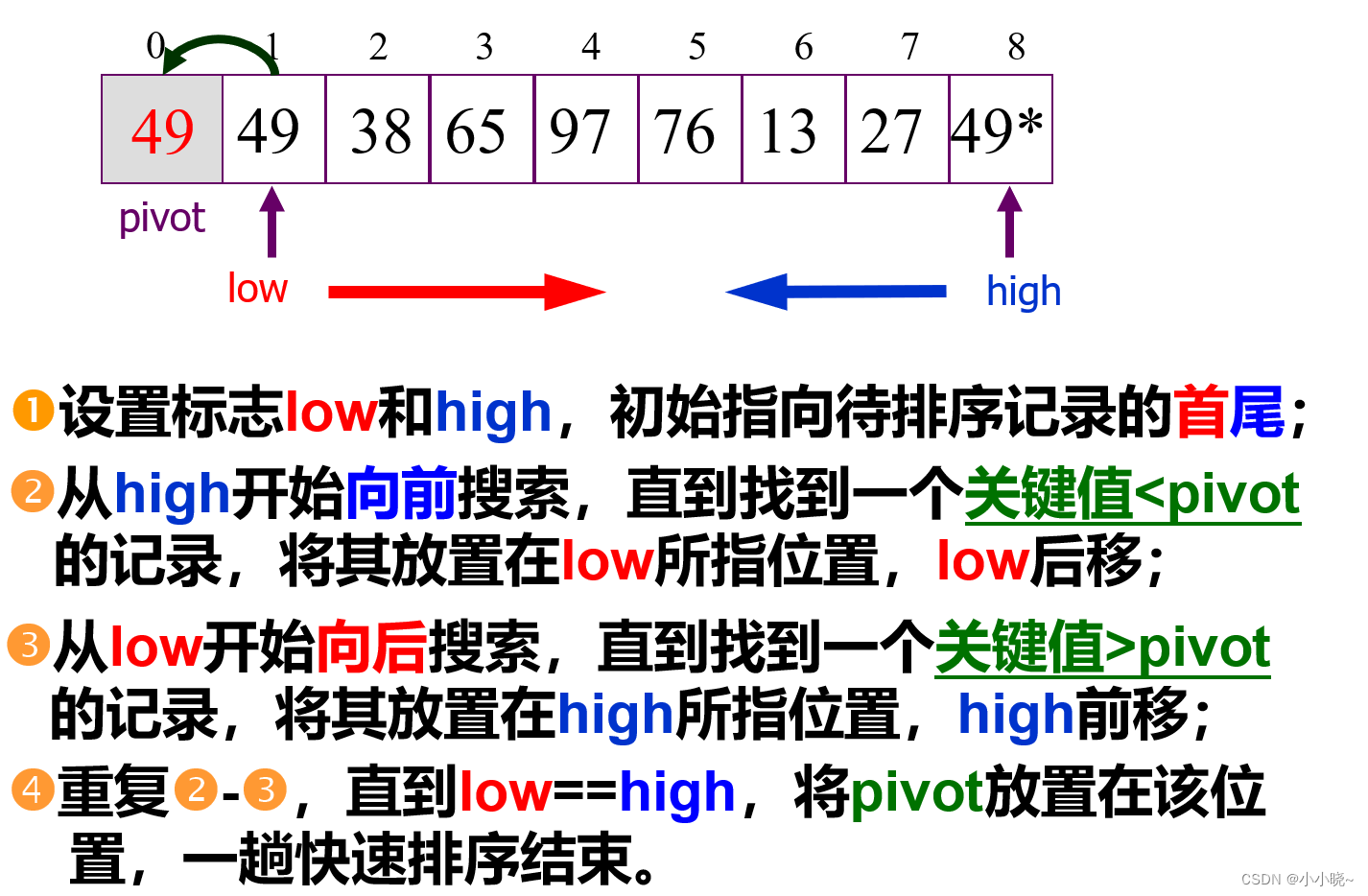
- 原理:
在待排序记录中任取一个记录(通常为第一个记录) , 作为枢轴(pivot)(基准),将其它记录分为两个子序列:
- 所有键值比它(枢轴)小的安置在一部分。
- 所有键值比它(枢轴)大的安置在另一部分。
(与基准相同的数据元素的处理:放在基准的右侧) - 把该数据元素放在这两部分的中间,这也是该数据元素排序后的最终位置这个过程称为一趟快速排序。
基准的选取:第一个数据元素、最后一个数据元素、中间位置的数据元素
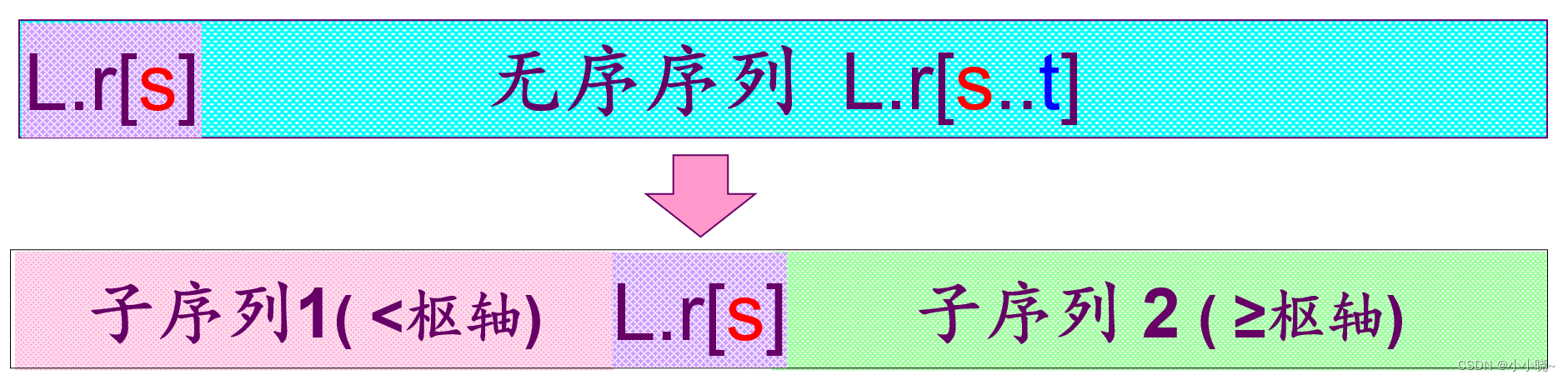
快速排序实现过程:
快速排序每趟的算法:
int Partition(SqList &L,int low,int high){keyType pivotkey;//数据类型 上述定义的包含关键字的数据类型L.r[0]=L.r[low];//保护 枢轴pivotkey=L.r[row].key;while(low<high){while(L.r[high].key>=pivotkey&&low<high) high--;//一直移动 直到if(low<high){L.r[low]=L.r[high];low++;}while(L.r[low].key<=pivotkey&&low<high) low++; //一直移动 直到if(low<high){L.r[high]=L.r[low];high--;}}L.r[low]=L.r[0];return low;
}
算法分析:
快速排序:(小规模数据 不适合快排)
void QuickSort(SqList &L,int low,int high){int pivotloc;if(low<high){pivotloc=Partition(L,low,high);QuickSort(L,low,pivotloc-1);QuickSort(L,pivotloc+1,high);}
}int Partition(SqList &L,int low,int high){keyType pivotkey;//数据类型 上述定义的包含关键字的数据类型L.r[0]=L.r[low];//保护 枢轴pivotkey=L.r[row].key;while(low<high){while(L.r[high].key>=pivotkey&&low<high) high--;//一直移动 直到if(low<high){L.r[low]=L.r[high];low++;}while(L.r[low].key<=pivotkey&&low<high) low++; //一直移动 直到if(low<high){L.r[high]=L.r[low];high--;}}L.r[low]=L.r[0];return low;
}递归!!!
算法评价:不稳定排序
时间复杂度: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 最好情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 平均情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 最差情况: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( l o g 2 n ) − O ( n ) O(log_{2}n)-O(n) O(log2n)−O(n)
-
最差情况

-
快速排序的最好情况:每次总是选到中间值作枢轴
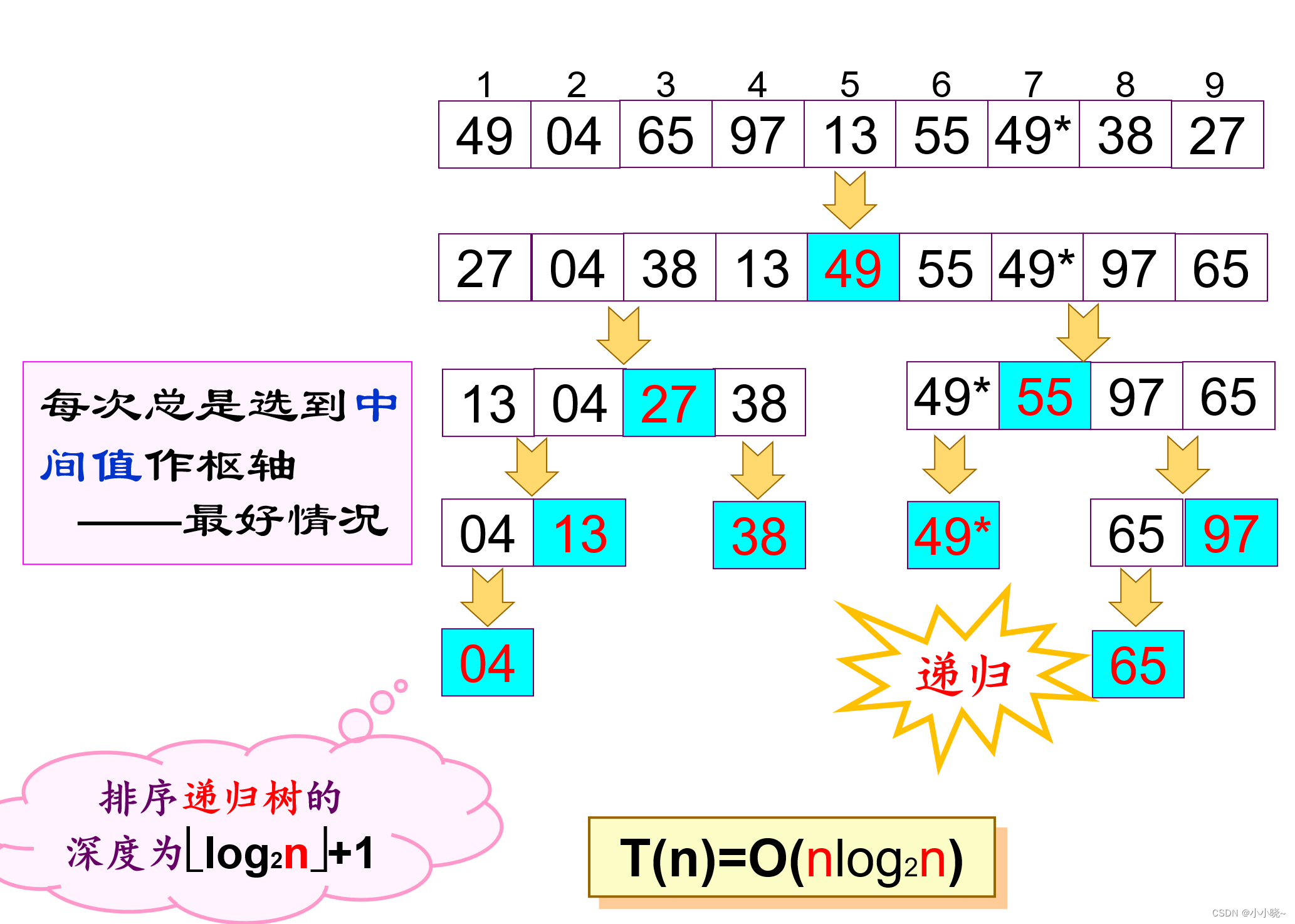
-
空间复杂度: O ( l o g 2 n ) − O ( n ) O(log_{2}n)-O(n) O(log2n)−O(n)
原因 使用递归的方法进行排序,需要使用到栈空间

图片来源 :快速排序时间复杂度和空间复杂度
2.冒泡排序
算法评价:稳定!
时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 最好情况: O ( n ) O(n) O(n)
- 平均情况: O ( n 2 ) O(n^2) O(n2)
- 最差情况: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( 1 ) O(1) O(1)
- 将待排序的数据元素的关键字顺次两两比较,若为逆序则将两个数据元素交换。
- 将序列照此方法从头到尾处理一遍称作一趟冒泡排序,它将关键字值最大的数据元素交换到排序的最终位置。
- 若某一趟冒泡排序没发生任何数据元素的交换,则排序过程结束。
- 对含
n个记录的文件排序最多需要n-1趟冒泡排序。
void BubbleSort( SqList &L){ int m, j, flag=1;//用于判断是否已经排好序 m=L.length-1;while((m>0)&&(flag= =1)){ flag=0;for(j=1;j<=m;j++) if(L.r[j].key>L.r[j+1].key){//冒泡排序是稳定的排序方法 没有等号 flag=1;//此次过程交换了 标记一下L.r[0]=L.r[j]; L.r[j]=L.r[j+1]; L.r[j+1]=L.r[0];}m--;}
}时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 最好情况: O ( n ) O(n) O(n)
- 平均情况: O ( n 2 ) O(n^2) O(n2)
- 最差情况: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( 1 ) O(1) O(1)
最好情况:n个数据元素,1趟冒泡排序,0次数据移动,n-1次比较。(初始的待排序序列恰好是有序)
最坏情况:n个数据元素, n-1趟冒泡排序。(初始的待排序序列恰好是逆序)
三、选择排序
选择排序:每次从待排序记录中选出关键字最小的记录,顺序放在已排序的记录序列的后面,直到全部排完为止
1. 简单选择排序
算法评价:不稳定!!!
时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 最好情况: O ( n 2 ) O(n^2) O(n2)
- 平均复杂度: O ( n 2 ) O(n^2) O(n2)
- 最差情况: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( 1 ) O(1) O(1)
!!!情况最好比较n-1次 无需交换,情况最差不是逆序
不论输入的待排序的数据是什么顺序,每一趟简单选择排序的比较次数不变,总的比较次数为:(n-1)+(n-2)+…+2+1=n(n-1)/2次
最好情况:第一趟找到的最小的恰好在第一个位置,不发生数据交换,…, 每一趟找到的最小的数据都不要交换,输入的待排序的数据恰好有序,总的数据移动次数为0次。
最坏情况:第一趟找到的最小的要交换到第一个位置,数据移动3次,…, 每一趟找到的最小的都要交换,数据移动 3次。总共n-1趟,总的数据移动次数3(n-1)次。
数据移动指的是交换 每次交换数据就要移动三次
适用于待排序元素较少的情况
算法实现:
void SelectSort( SqList &L)
{ int i, j, k;for(i=1;i<L.length;i++) { k=i; for(j=i+1;j<=L.length;j++)//查找最小的if(L.r[j].key<L.r[k].key) k=j;//if(i!=k){ L.r[0].key=L.r[i]; L.r[i]=r[k]; L.r[k]=L.r[0].key; }}
}
2. 堆排序
算法评价:不稳定
时间复杂度: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 最好情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 平均情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
- 最坏情况: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
空间复杂度: O ( 1 ) O(1) O(1)
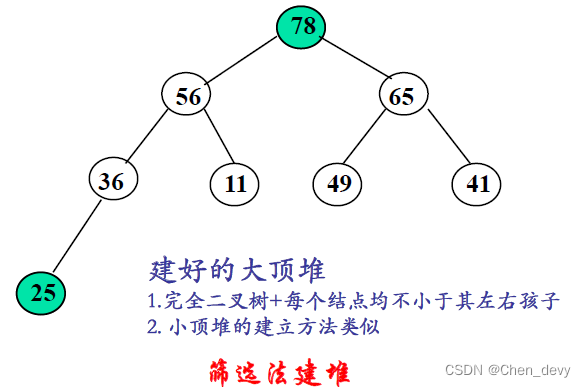
可将堆序列看成完全二叉树的顺序存储,堆顶元素(完全二叉树的根)必为序列中n个元素的最小值或最大值

初建堆(大顶堆):
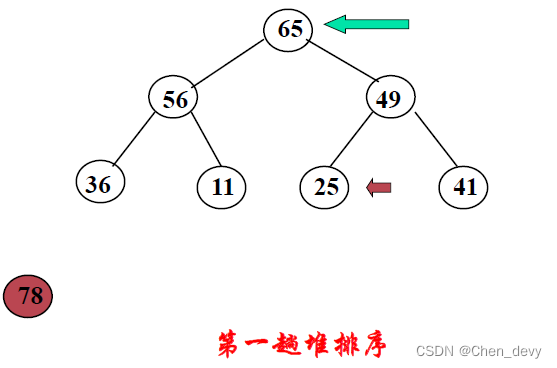
第一趟排序:
第二趟排序:

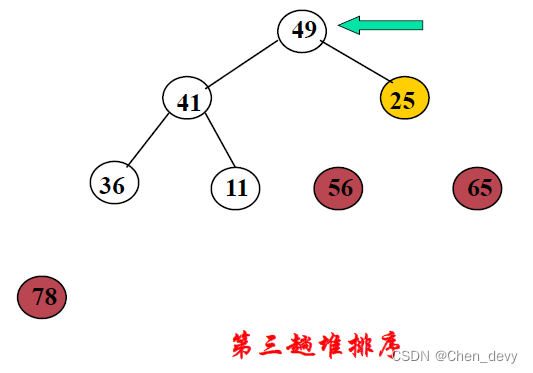
第三趟排序:
第四趟排序:
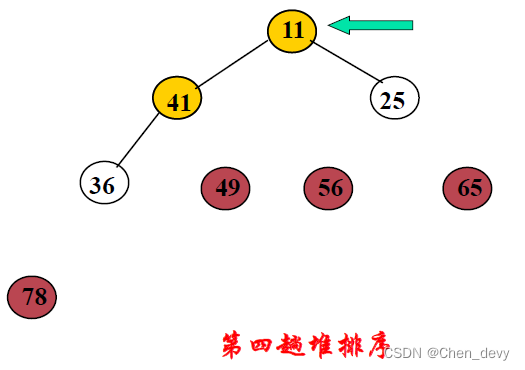
第五趟排序:
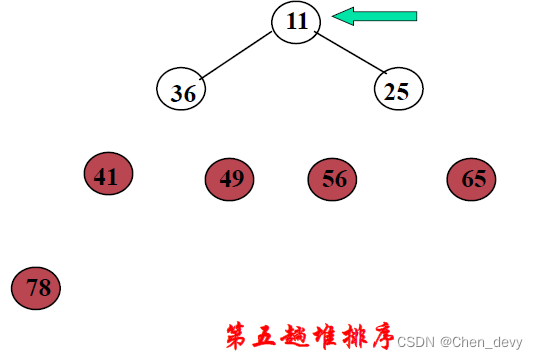
第六趟排序:
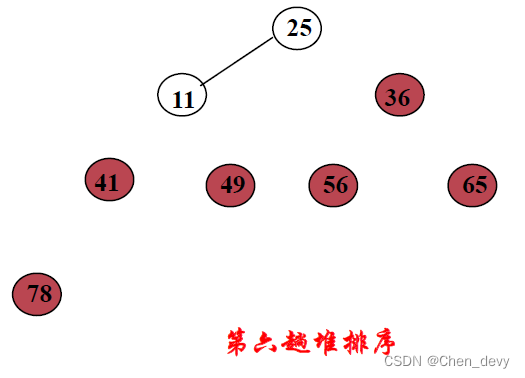
第七趟排序:
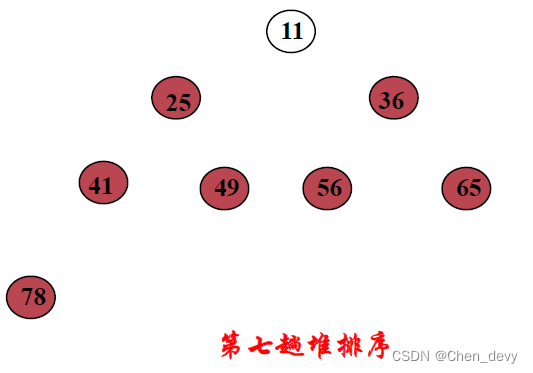
堆排序 完全排好序: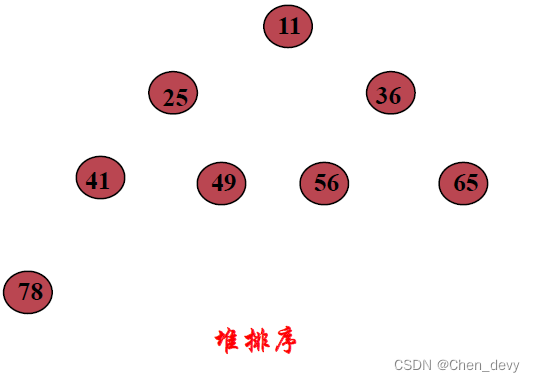

void HeapSort(SqList &L){ int i,j,k;for (i=L.Length/2;i>0;--i)//筛选法建堆,从n/2处开始调整HeapAdjust(L,i,L.Length); //调整以i为根结点的子树为一个大顶堆for(i=L.Length;i>1;--i)//n-1趟堆排序,当前大顶堆中的数据元素i个,L.r[1]中是i个数据元素中的最大值{ L.r[0]=L.r[i];L.r[i]=L.r[1];L.r[1]=L.r[0];//将堆中最大的数据元素L.r[1]交换到第i个位置,也是它最终排序后的位置HeapAdjust(L,1,i-1);////堆中数据元素个数为i-1,将i-1个数据元素重新调整为大顶堆}
}
//函数HeapAdjust(L,i,L.Length)-调整以i为根结点的子树为一个大顶堆void HeapAdjust(SqList &L,int s,int m)
//调整以s为根结点的子树为一个大顶堆,堆中最大的数据元素编号为m,且以s为根的子树中除根结点s外,均满足大顶堆的定义
{ int j;L.r[0]=L.r[s]; //记录下 根节点的信息for(j=2*s, j<=m; j=j*2){ if(j<m && L.r[j].key< L.r[j+1].key) ++j;//j为左、右孩子中最大的那个if(L.r[0].key>=L.r[j].key) break; L.r[s]=L.r[j];s=j;}L.r[s]=L.r[0];//
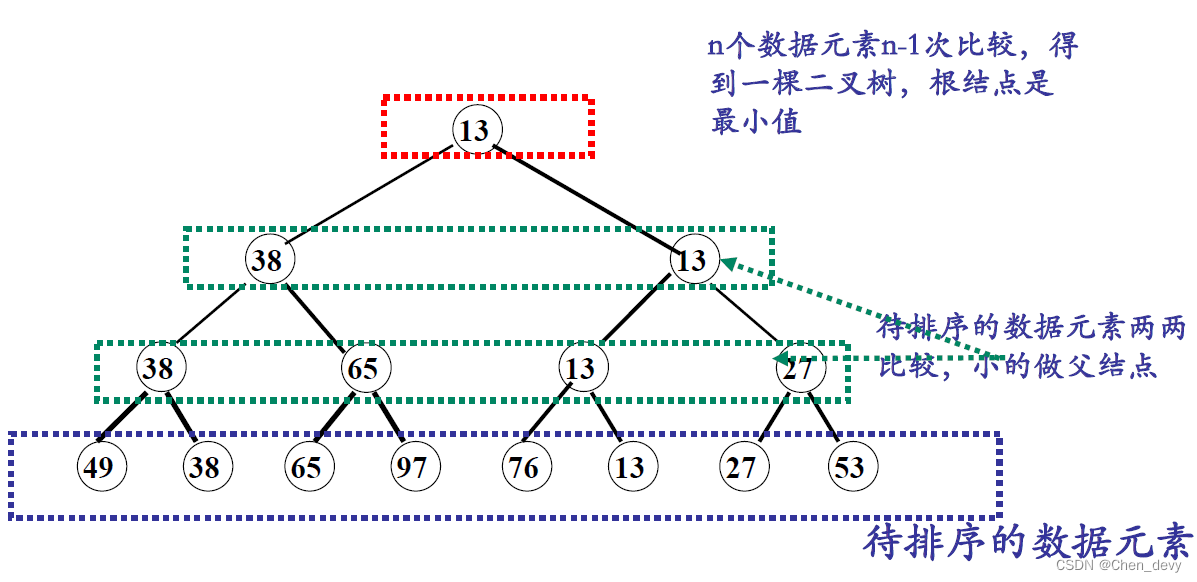
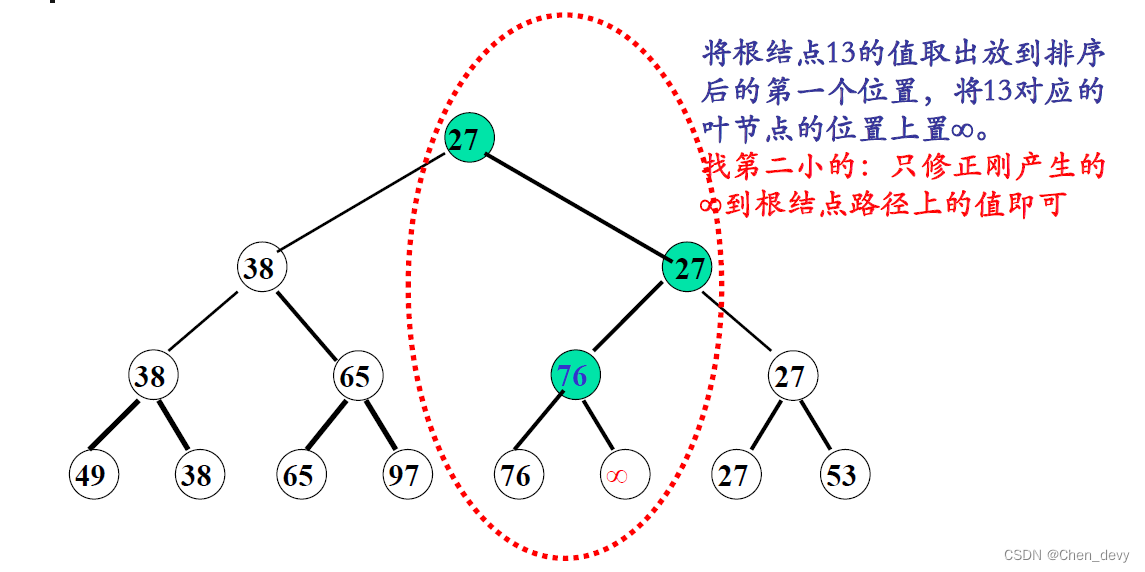
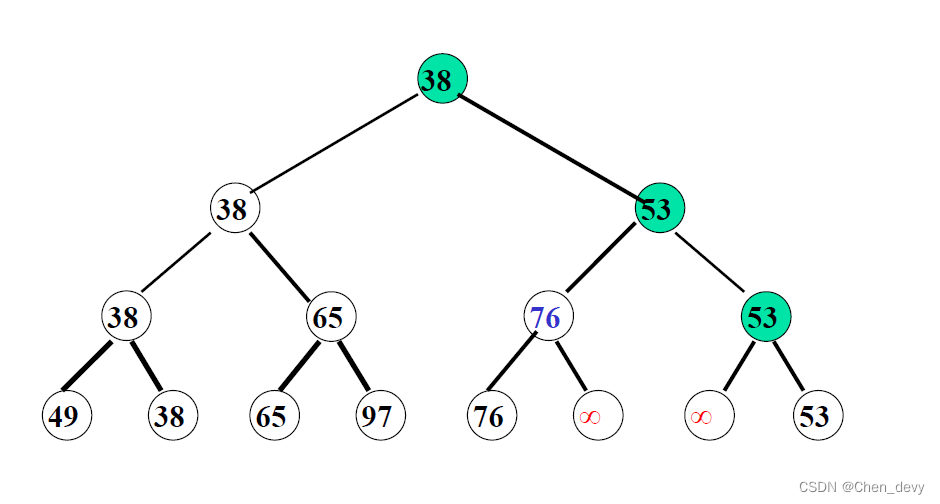
}3. 树排序
树排序将时间复杂度降为 O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n),但需要的辅助空间增加
四、归并排序(2-路归并排序)
分治策略
算法评价:稳定!!!
时间复杂度为: O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n)
空间复杂度: O ( n ) O(n) O(n)

归并排序:每次将两个或两个以上的有序表组合成一个新的有序表
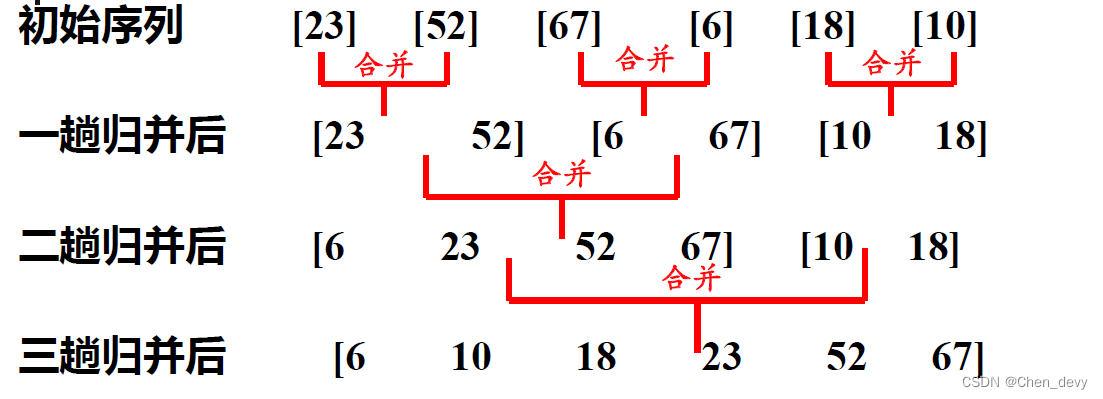
排序过程:
设初始序列含有n个记录,则可看成n个有序的子序列,每个子序列长度为1 两两合并,得到 n / 2 n/2 n/2 个长度为2或1的有序子序列
再两两合并,……如此重复,直至得到一个长度为n的有序序列为止
自底向上:
自项向下:

//自底向上
void Merge (ElemType SR[], Elemtype TR[], int i, int m, int n){ int j, k;// 将有序的序列 SR[s..m] 和 SR[m+1..t]归并为有序的序列 TR[s..t]for (j=m+1, k=i;i<=m && j<=n;++k){ // i为第一个有序序列 SR[s..m] 当前正在查看的数据,该序列的第一个数据元素在s处;// j为第二个有序序列 SR[m+1..t]当前正在查看的数据,该序列的第一个数据元素在m+1处;// k为合并后的有序序列 TR[s..t]的存放位置,第一个位置为sif (SR[i].key<=SR[j].key) TR[k] = SR[i++];else TR[k] = SR[j++];}if (i<=m)for(;i<=m;i++,k++) //第一个有序序列 还有数据没有比较,将其复制到合并后的序列;TR[k] = SR[i]; if (j<=n) for(;j<=n;j++,k++)// 第二个有序序列 还有数据没有比较,将其复制到合并后的序列 TR[k] = SR[j];
}
//自底向上 合并 合并 合并
void MSort ( ElemType SR[], ElemType TR1[], int s, int t )
{ // 将SR[s..t] 归并排序为 TR1[s..t]ElemType TR2[MAXSIZE]; int m;if (s==t) TR1[s]=SR[s];//序列中只有一个数据元素,序列自然有序else { //序列中包含2个或2个以上数据元素m = (s+t)/2;//计算序列的中间位置,以此为界划分为2个序列MSort (SR, TR2, s, m); //对第一个子序列递归调用归并排序算法,使其有序MSort (SR, TR2, m+1, t); //对第二个子序列递归调用归并排序算法,使其有序Merge (TR2, TR1, s, m, t); //将2个有序子序列合并为一个有序序列}
}2-路归并排序算法评价:
五、基数排序
不通过待排序数据元素之间的比较
根据关键字本身的性质进行排序
分配排序,桶排序,基数排序
1. 桶排序(适合元素关键字值集合并不大)

2. 基数排序
时间复杂度: O ( d ( n + 2 r d ) ) O(d(n+2rd)) O(d(n+2rd))
空间复杂度: O ( r d ) O(rd) O(rd)
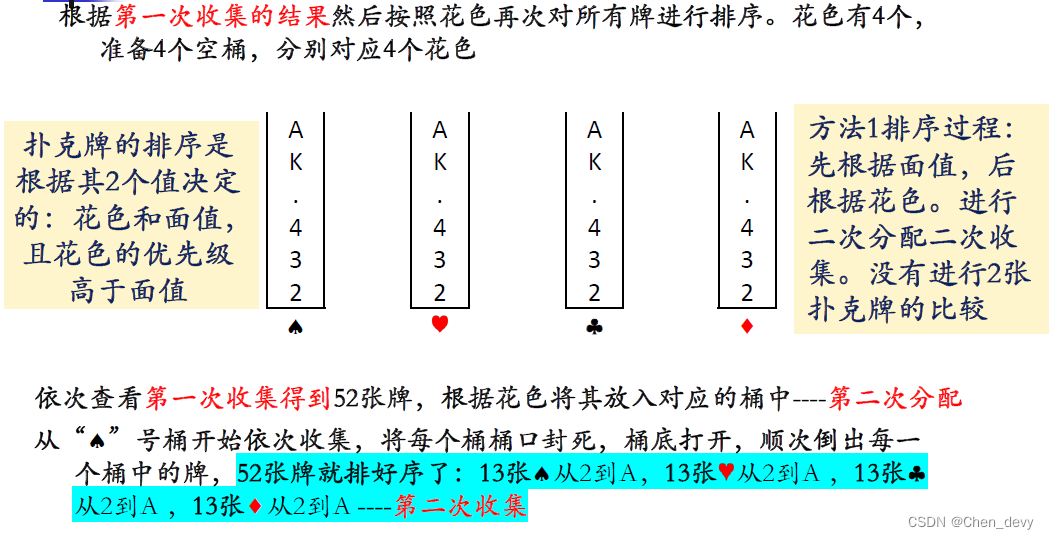
方法一:优先级 由低到高

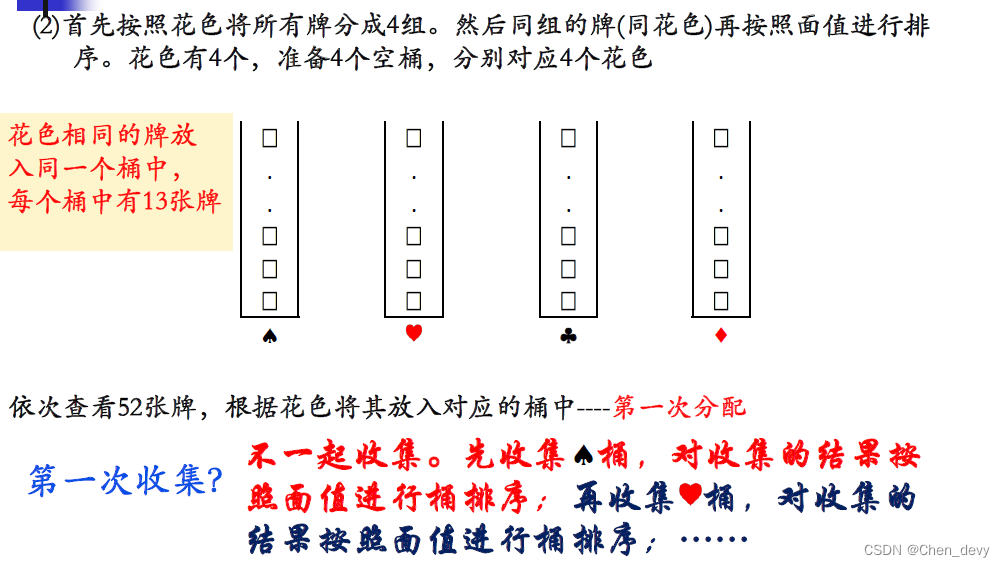
方法二 由高到低
基数排序是一种借助“多关键字排序”的思想来实现“单关键字排序”的内部排序算法。
通常采用低位优先—简单方便





基数排序(Radix Sort)是一种非比较型排序算法,它通过将待排序的元素分成多个关键字进行排序,然后依次对每个关键字进行分配和收集,从而完成整个排序过程。基数排序适用于处理整数或字符串等类型的排序问题。下面是基数排序的详细分析和解释:
基数排序的基本原理
基数排序的基本思想是将待排序的记录(元素)看作是由多个关键字组成的,每次按一个关键字对记录进行分配和收集,逐步完成排序。通常有两种方法:
- 最高位优先法(MSD,Most Significant Digit):先按最高位进行排序,再按次高位进行排序,依此类推,直到按最低位排序。
- 最低位优先法(LSD,Least Significant Digit):先按最低位进行排序,再按次低位进行排序,依此类推,直到按最高位排序。
基数排序的实现步骤
基数排序可以分为以下几个步骤进行:
-
初始化静态链表:
- 将待排序的数据元素存放在一个静态链表中,初始链表的顺序与原始数据的顺序相同。
- 用
next指针将所有数据元素连接起来,最后一个元素的next指针为-1,表示链表的尾结点。
-
分配(Distribute):
- 按照当前关键字(从最低位开始)对数据元素进行分配。
- 根据当前关键字的值,将数据元素分配到不同的桶(或链表)中。
-
收集(Collect):
- 将所有桶中的数据元素按顺序收集起来,重新连接成一个链表。
- 完成一次对当前关键字的排序。
-
重复上述步骤:
- 对下一个关键字重复进行分配和收集,直到所有关键字都排序完毕。
基数排序的代码实现
以下是给出的基数排序的代码实现及其详细分析:
#define MAX_NUM_OF_KEY 8//关键字个数最大值
#define radix10//队列个数
#define MAX_SPACE 1000
typedef struct {Keystype keys[MAX_NUM_OF_KEY];//……int next;
}SLCell;typedef struct {SLCell R[MAX_SPACE];int keynum; // 关键字个数int recnum; // 待排序数据元素个数
} SLList;// 定义一个数组类型,用于存放每个桶的头指针和尾指针
typedef int ArrType[radix];void Distribute(SLCell R[], int i, ArrType &f, ArrType &r, int head) {// 初始化每个桶的头指针数组 f,全部设置为 -1,表示空桶for (int j = 0; j < radix; j++) f[j] = -1;// 遍历链表,将每个元素按第 i 个关键字值分配到对应的桶中for (int p = head; p != -1; p = R[p].next) { int j = ord(R[p].keys[i]); // 取 R[p] 的第 i 个关键字// 如果当前桶是空的,则设置该桶的头指针为当前元素if (f[j] == -1)f[j] = p;else R[r[j]].next = p; // 否则将当前元素链接到当前桶的尾部r[j] = p; // 更新当前桶的尾指针为当前元素}
}void Collect(SLCell R[], int i, ArrType f, ArrType r, int &head) {// 找到第一个非空的桶,并设置为链表的头int j = 0;while (j < radix && f[j] == -1)j++;head = f[j];// 设置 t 为当前连接链表的尾部int t = r[j];// 依次连接其他桶,形成新的链表while (j < radix) {j++;while (j < radix && f[j] == -1)j++;if (j < radix) {R[t].next = f[j]; // 将 t 的 next 指向 f[j]t = r[j]; // 更新 t 为当前桶的尾部}}// 最后一个节点的 next 设为 -1,表示链表结束R[t].next = -1;
}void RadixSort(SLList &L) {// 初始化静态链表,将数据元素按初始顺序连接起来for (int j = 0; j < L.recnum - 1; j++) L.R[j].next = j + 1; // 设置每个元素的 next 指向下一个元素L.R[L.recnum - 1].next = -1; // 最后一个元素的 next 指向 -1,表示链表结束int head = 0; // 初始化链表的头指针为第一个元素ArrType f, r; // 桶的头指针数组 f 和尾指针数组 r// 对每个关键字依次进行分配和收集for (int i = 0; i < L.keynum; i++) {Distribute(L.R, i, f, r, head); // 根据第 i 个关键字进行分配Collect(L.R, i, f, r, head); // 将分配好的桶按顺序收集成新的链表}
}下面是逐行解释给出的基数排序代码:
typedef struct {SLCell R[MAX_SPACE];int keynum; // 关键字个数int recnum; // 待排序数据元素个数
} SLList;// 定义一个数组类型,用于存放每个桶的头指针和尾指针
typedef int ArrType[radix];void Distribute(SLCell R[], int i, ArrType &f, ArrType &r, int head) {// 初始化每个桶的头指针数组 f,全部设置为 -1,表示空桶for (int j = 0; j < radix; j++) f[j] = -1;// 遍历链表,将每个元素按第 i 个关键字值分配到对应的桶中for (int p = head; p != -1; p = R[p].next) { int j = ord(R[p].keys[i]); // 取 R[p] 的第 i 个关键字// 如果当前桶是空的,则设置该桶的头指针为当前元素if (f[j] == -1)f[j] = p;else R[r[j]].next = p; // 否则将当前元素链接到当前桶的尾部r[j] = p; // 更新当前桶的尾指针为当前元素}
}void Collect(SLCell R[], int i, ArrType f, ArrType r, int &head) {// 找到第一个非空的桶,并设置为链表的头int j = 0;while (j < radix && f[j] == -1)j++;head = f[j];// 设置 t 为当前连接链表的尾部int t = r[j];// 依次连接其他桶,形成新的链表while (j < radix) {j++;while (j < radix && f[j] == -1)j++;if (j < radix) {R[t].next = f[j]; // 将 t 的 next 指向 f[j]t = r[j]; // 更新 t 为当前桶的尾部}}// 最后一个节点的 next 设为 -1,表示链表结束R[t].next = -1;
}void RadixSort(SLList &L) {// 初始化静态链表,将数据元素按初始顺序连接起来for (int j = 0; j < L.recnum - 1; j++) L.R[j].next = j + 1; // 设置每个元素的 next 指向下一个元素L.R[L.recnum - 1].next = -1; // 最后一个元素的 next 指向 -1,表示链表结束int head = 0; // 初始化链表的头指针为第一个元素ArrType f, r; // 桶的头指针数组 f 和尾指针数组 r// 对每个关键字依次进行分配和收集for (int i = 0; i < L.keynum; i++) {Distribute(L.R, i, f, r, head); // 根据第 i 个关键字进行分配Collect(L.R, i, f, r, head); // 将分配好的桶按顺序收集成新的链表}
}
- 数据结构定义:
typedef struct {SLCell R[MAX_SPACE]; // 存放待排序数据元素的数组int keynum; // 关键字个数int recnum; // 待排序数据元素个数
} SLList;
SLCell R[MAX_SPACE]:存放待排序数据元素的数组。int keynum:关键字的个数。int recnum:待排序数据元素的个数。
typedef int ArrType[radix];
- 定义一个数组类型,用于存放每个桶的头指针和尾指针。
- 分配函数
Distribute:
void Distribute(SLCell R[], int i, ArrType &f, ArrType &r, int head) {// 初始化每个桶的头指针数组 f,全部设置为 -1,表示空桶for (int j = 0; j < radix; j++) f[j] = -1;// 遍历链表,将每个元素按第 i 个关键字值分配到对应的桶中for (int p = head; p != -1; p = R[p].next) { int j = ord(R[p].keys[i]); // 示意性操,取 R[p] 的第 i 个关键字// 如果当前桶是空的,则设置该桶的头指针为当前元素if (f[j] == -1)f[j] = p;else R[r[j]].next = p; // 否则将当前元素链接到当前桶的尾部r[j] = p; // 更新当前桶的尾指针为当前元素}
}
Distribute函数按第i个关键字值对数据元素进行分配。- 初始化桶的头指针数组
f为-1,表示空桶。 - 遍历链表,将每个数据元素按当前关键字值分配到对应的桶中。
- 更新桶的头指针和尾指针。
- 收集函数
Collect:
void Collect(SLCell R[], int i, ArrType f, ArrType r, int &head) {// 找到第一个非空的桶,并设置为链表的头int j = 0;while (j < radix && f[j] == -1)j++;//找到第一个 不是-1的head = f[j];// 设置 t 为当前连接链表的尾部int t = r[j];// 依次连接其他桶,形成新的链表while (j < radix) {// j++;while (j < radix && f[j] == -1)j++;//找到下一个 不是-1的if (f[j]!=-1) {R[t].next = f[j]; // 将 t 的 next 指向 f[j]t = r[j]; // 更新 t 为当前桶的尾部}}// 最后一个节点的 next 设为 -1,表示链表结束R[t].next = -1;
}
Collect函数将分配好的桶按顺序收集成新的链表。- 找到第一个非空的桶,设置为链表的头。
- 依次连接其他桶,形成新的链表。
- 设置最后一个节点的
next为-1,表示链表结束。
- 基数排序主函数
RadixSort:
void RadixSort(SLList &L) {// 初始化静态链表,将数据元素按初始顺序连接起来for (int j = 0; j < L.recnum - 1; j++) L.R[j].next = j + 1; // 设置每个元素的 next 指向下一个元素L.R[L.recnum - 1].next = -1; // 最后一个元素的 next 指向 -1,表示链表结束int head = 0; // 初始化链表的头指针为第一个元素ArrType f, r; // 桶的头指针数组 f 和尾指针数组 r// 对每个关键字依次进行分配和收集for (int i = 0; i < L.keynum; i++) {Distribute(L.R, i, f, r, head); // 根据第 i 个关键字进行分配Collect(L.R, i, f, r, head); // 将分配好的桶按顺序收集成新的链表}
}
RadixSort函数是基数排序的主函数。- 初始化静态链表,将数据元素按初始顺序连接起来。
- 初始化链表的头指针为第一个元素。
- 定义桶的头指针数组
f和尾指针数组r。 - 对每个关键字依次进行分配和收集,完成排序。
时间性能
平均的时间性能
时间复杂度为O(nlogn):快速排序、堆排序和归并排序
时间复杂度为 O ( n 2 ) O(n^2) O(n2):直接插入、冒泡和简单选择排序
时间复杂度为 O ( n ) O(n) O(n): 基数排序
当待排记录序列按关键字顺序有序时
直接插入和冒泡排序: O ( n ) O(n) O(n)
快速排序: O ( n 2 ) O(n_2) O(n2) 。
简单选择排序、堆排序和归并排序的时间性能不随记录序列中关键字的分布而改变。
空间性能指的是排序过程中所需的辅助空间大小
所有的简单排序方法(包括:直接插入、起泡和简单选择) 和堆排序的空间复杂度为O(1);
快速排序为O(logn),为递归程序执行过程中,栈所需的辅助空间;
归并排序所需辅助空间最多,其空间复杂度为 O(n);
链式基数排序需附设队列首尾指针,则空间复杂度为 O(rd)。
相关文章:

【数据结构】排序(直接插入、折半插入、希尔排序、快排、冒泡、选择、堆排序、归并排序、基数排序)
目录 排序一、插入排序1.直接插入排序2.折半插入排序3.希尔排序 二、交换排序1.快速排序2.冒泡排序 三、选择排序1. 简单选择排序2. 堆排序3. 树排序 四、归并排序(2-路归并排序)五、基数排序1. 桶排序(适合元素关键字值集合并不大)2. 基数排序基数排序的…...

MongoDB ObjectId 详解
MongoDB ObjectId 详解 MongoDB 是一个流行的 NoSQL 数据库,它使用 ObjectId 作为文档的唯一标识符。ObjectId 是一个 12 字节的 BSON 类型,它在 MongoDB 中用于保证每个文档的唯一性。本文将详细解释 ObjectId 的结构、生成方式以及它在 MongoDB 中的应用。 ObjectId 的结…...
)
大数据-11-案例演习-淘宝双11数据分析与预测 (期末问题)
目录 第一部分 Hadoop是什么 官方解释: 个人总结 HDFS 是什么? 官方解释: 个人总结 yarn是什么? 官方解释: 个人总结 mapreduce,spark 是什么? 官方解释: MapReduce Spark 个人总结 MapReduce Spa…...

Kubernetes集群监控,kube-prometheus安装教程,一键部署
Kube-prometheus介绍 Kube-prometheus 是一个用于监控 Kubernetes 集群的完整解决方案。它基于 Prometheus 生态系统,提供了一整套预配置的组件和配置文件,以便轻松地在 Kubernetes 上部署和运行 Prometheus 监控系统。 Kube-prometheus 主要包括以下组…...
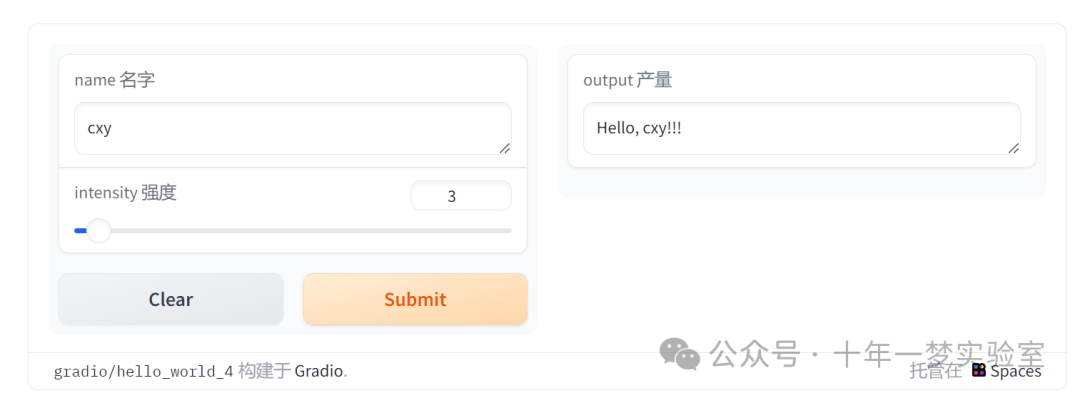
【Gradio】快速入门
https://www.gradio.app/ Gradio 是一个开源 Python 软件包https://github.com/gradio-app/gradio ,可以让你快速为机器学习模型、API 或任何任意 Python 函数创建一个演示或网络应用程序。然后,您就可以使用 Gradio 内置的分享功能,在几秒钟…...
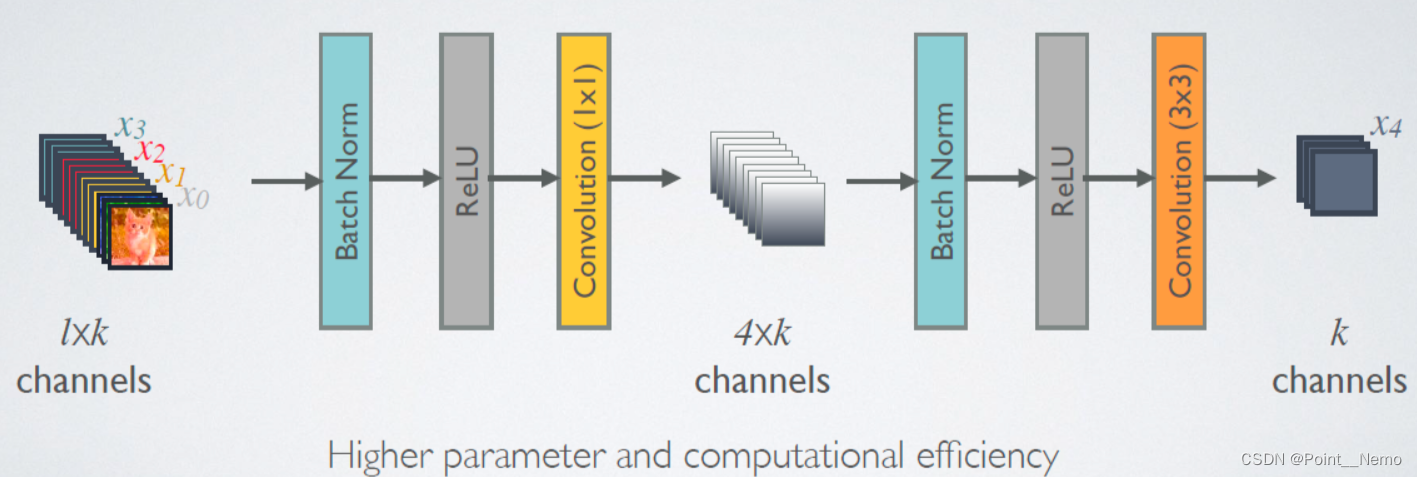
深度学习Day-19:DenseNet算法实战与解析
🍨 本文为:[🔗365天深度学习训练营] 中的学习记录博客 🍖 原作者:[K同学啊 | 接辅导、项目定制] 要求: 根据 Pytorch 代码,编写出 TensorFlow 代码研究 DenseNet 与 ResNetV 的区别改进思路是…...

基于openssl实现AES ECB加解密
AES加密,全称高级加密标准(Advanced Encryption Standard),是一种广泛使用的对称加密算法,用于保护电子数据的安全。以下是AES加密的基本原理和特点: 基本概念 对称加密:AES是一种对称加密算法…...

Git:从配置到合并冲突
目录 1.前言 2.Git的下载与初始化配置 3.Git中新建仓库 4.Git的工作区域和文件状态 5.Git中查看操作和提交记录 6.Git中添加和提交文件 7.Git中回退提交版本 8.Git中查看版本间的差异 9.Git中删除文件 10.Git中忽略指定文件 11.Git中配置SSH密钥 12.Git中关联克隆仓库 13.Git中…...

leetcode hot100 之 最长公共子序列
题目 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。 一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(…...
短剧APP开发,新的“财富”
在数字化时代,开发短剧APP不仅是顺应潮流的必然选择,更是抓住市场机遇的关键所在。为确保短剧APP能有效地吸引并留住用户,以下是一些主要功能及其介绍: 1、短剧搜索 关键词搜索:用户可以通过输入关键词(如…...

Uniapp与第三方应用数据通讯
首先说明一点,这个只是uniapp代码编写的应用之间相互传递数据,uniapp编写的与其他语言编写的我尚不知道能不能传递。 应用1: plus.runtime.launchApplication({pname: "应用的appid",// extra 中可以自定数据,url和da…...

AI大模型战场:通用大模型与垂直大模型的角逐
随着人工智能技术的迅猛发展,AI大模型已成为推动科技进步的重要力量。然而,在AI大模型的战场上,通用大模型与垂直大模型之间的分化日益明显。两者各有其独特的优势和潜力,在不同的应用场景中发挥着重要作用。那么,在这…...

linux的一些知识点分享-------关于操作维护的一些知识点
Apache服务器的监听端口,默认为() Apache服务器的监听端口,默认为80。 vsftpd中,可以不需提供账号密码就能进行访问的用户是( ) 在vsftpd(Very Secure FTP Daemon)中,可以不需要提供账号密码就能进行访问的用户通常是匿名用户。…...
Python使用tkinter库设置背景图片、label显示位置和label设置显示图片
tkinter 设置背景图片 label显示位置 label设置显示图片 from tkinter import * import tkinter as tk from PIL import ImageTk from PIL import Imagedef get_img(filename, width, height):im Image.open(filename).resize((width, height))im ImageTk.PhotoImage(im)…...

OpenStack是什么?
OpenStack是一个开源的云计算管理平台项目,它是一系列软件开源项目的组合。该项目由美国国家航空航天局(NASA)和Rackspace合作研发并发起,旨在提供实施简单、可大规模扩展、丰富、标准统一的云计算管理平台。OpenStack不仅是一个软…...

2024下《系统规划与管理师》50个高频考点汇总!背就有效
2024上半年软考考试已经结束,有不少小伙伴已经开始准备下半年软考了,但是大家要注意:今年高项仅考上半年一次,下半年考的高级科目只有系规难度相对较低,系规需要学习的内容比高项少很多,高项第四版教程731页…...
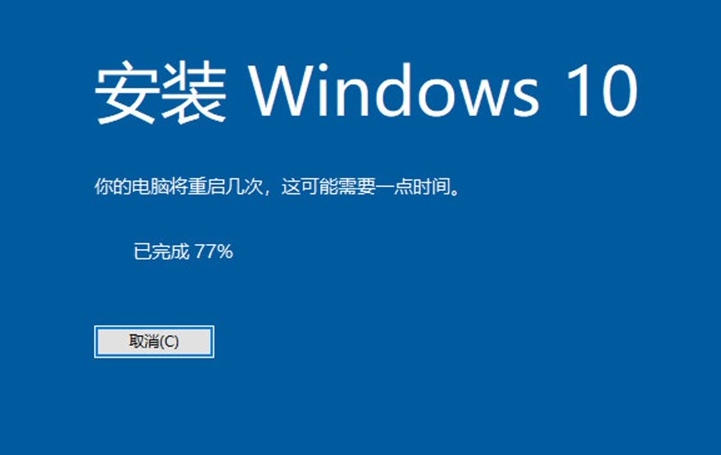
软件游戏提示msvcp140.dll丢失的原因分析及解决方法
在计算机使用过程中,我们经常会遇到一些错误提示,其中之一就是“计算机缺失msvcp140.dll”。那么,这个错误是什么意思呢?它会造成哪些问题?小编将从以下几个方面进行详细解析。 一,了解msvcp140.dll是什么 …...

备战 清华大学 上机编程考试-冲刺前50%,倒数第3天
T1:水滴 - 模拟 这是一个经典的游戏。 在一个 𝑛𝑚 的棋盘上,每一个格子中都有一些水滴。 玩家的操作是,在一个格子中加一滴水。 当一个格子中的水滴数超过了 4,这一大滴水就会因格子承载不住而向外扩散。扩散的规…...

docker的安装及docker常用命令
目录 环境介绍docker卸载docker安装docker镜像命令查看docker可用的镜像查看docker可安装的镜像安装镜像删除镜像 docker容器命令查看容器启动容器启动示例进入容器内部停止容器删除容器容器和主机之间的文件复制 docker网络命令创建docker网络查看docker网络删除docker网络 do…...

Dell服务器根据GPU温度调整风扇转速
前言 dell服务器自动风扇是根据CPU温度来调速的,我跑AI的时候cpu温度不高但是GPU温度很高导致显卡卡死PVE虚拟机直接挂起无法运行,我看了下也没有基于显卡温度调速的脚本,于是我就自己写了一个 基于ipmi工具 乌班图等linux先安装ipmi apt …...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...