基于RandLA-Net深度学习模型的激光点云语义分割
一、场景要素语义分割部分的文献阅读笔记
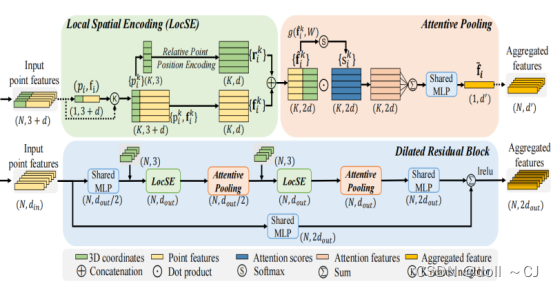
RandLA-Net是一种高效、轻量级的神经网络,其可直接逐点推理大规模点云的语义标签。RandLA-Net基于随机点采样获得了显著的计算和内存效率,并采用新的局部特征聚合模块有效地保留了几何细节,弥补了随机采样可能丢失关键特征的不足。其中,局部特征聚合器(Local Feature Aggregation,LFA)由局部空间编码、自适应注意力池化以及扩张残差块三个子模块组成。
局部特征聚合器的三个重要子模块:
- 局部空间编码(Local Spatial Encoding,LocSE)。 首先基于K最近邻算法找到各输入点的K个邻近点,然后逐输入点通过一个共享的多层感知机进行相对位置编码,继而进行特征堆叠和特征增强以获取每个输入点的邻域特征。局部空间编码单元显式地嵌入所有邻近点的空间三维坐标,这样可以明确地学习到输入点周围邻域的局部几何模式,从而有利于整个网络有效地学习复杂的局部结构。
- 自适应注意力池化(Attentive Pooling,AP)。首先将局部空间编码所提取到的邻域特征通过共享权重多层感知机和Softmax函数组合进行注意力得分计算,然后依据注意力分数对得到的局部特征进行加权求和以得到更为准确的特征向量组。
- 扩张残差块(Dilated Residual Block,DRB)。一个扩张残差块包含两次局部空间编码模块与自适应注意力池化模块组合,扩张残差块基于短接操作将输入特征和增强后的特征求和输出,其目的在于增加感受野、加快学习速度和持续提升模型精度。
RandLA-Net网络模型的随机采样结合了点概率标记的方法,点概率由距离和搜索权重计算,这样可以防止一个点被多次选中,也可以防止数量多的类别点被多次选中,而数量少的类别点很少被选中。同时,RandLA-Net网络模型在推理过程中会将输入点云进行下采样且记录原始点云与下采样后的最近邻关系,采用距离最近点标签预测一致的原则输出原始输入点云的预测结果,从而加快模型推理速度。
二、RandLA-Net点云语义分割项目代码逐行解析
项目环境配置:
操作系统:Ubuntu 20.04
Python解释器:Python 3.6(本实验中,若版本大于3.6则无法编译compile_op.sh文件)
CUDA版本:9.0
cuDNN版本:7.3.1
Tensorflow框架版本:1.11.0
配置顺序:CUDA/cuDNN -> tensorflow-1.11.0 -> 配置项目依赖及编译.sh文件
百度网盘链接:
https://pan.baidu.com/s/10hrjVJ3RUOlx_50OH2J2gw
模型测试结果可视化:

电力廊道场景应用下的文件结构说明:
① RandLA-Net-master\main_Power.py
该文件实现了Power类,该类主要完成数据集的划分(训练集、验证集和测试集)、生成输入数据流、数据预处理(数据增强、中心化等)等功能。
② RandLA-Net-master\RandLANet.py
该文件实现了Network类,该类主要完成模型超参数设置、模型推理结构、模型训练结构、模型精度评价结构等功能,包含了注意力池化(att_pooling)、近邻点坐标/特征聚合(gather_neighbour)、最近邻插值上采样(nearest_interpolation)、随机采样(random_sample)等编码模块。
③ RandLA-Net-master\tester_Power.py
该文件实现了ModelTester类,该类主要完成模型对测试数据的推理预测与存储对应预测结果点云。
④ RandLA-Net-master\helper_tool.py
该文件主要实现了ConfigPower类、DataProcessing类,二者实现模型训练超参数调试优化和数据预处理(点云数据网格下采样、KD树索引建立、原始点云与下采样后点云最近距离点索引存储)等功能函数。
⑤ RandLA-Net-master\helper_ply.py
该文件实现了.ply存储格式的点云数据读取和写入功能。
⑥ RandLA-Net-master\DataPreds_IOU.py
该文件实现了对点云预测结果的精度评价文件输出(.txt格式)以及预测点云标签三维空间分布数据生成。
⑦ RandLA-Net-master\utils\data_prepare_Power.py
该文件用于将S3DIS DataSet文件树数据集转换为.ply格式存储点云数据。该文件主要完成点云数据.ply格式转换、点云网格下采样、网格下采样后的KD树构建存储、存储原始所有点云在网格下采样点云中距离最近的点索引集合等功能,目的在于加快邻域点搜索和点云上采样还原。
⑧ RandLA-Net-master\data
该文件夹包含input_0.xxx、original_ply和Power三个文件夹。其中,Power文件夹存放S3DIS DataSet文件树结构的电力档段数据集,input_0.xxx存放网格下采样后的点云数据,original_ply存放转换为.ply格式存储的原始点云数据。
⑨ RandLA-Net-master\utils\meta
该文件夹包含anno_paths.txt和class_names.txt两个文件,anno_paths.txt文件存储电力档段的各要素点云集合文件夹名(如Area_0/Annotations),class_names.txt文件顺序存储要素类别名称。该文件夹用于点云类别标签转换赋值。
⑩ RandLA-Net-master\PowerTXT
存放由DataPreds_IOU.py文件生成的预测后三维点云类别标签空间分布数据和自定义精度评价文件(.txt格式)。
⑩① RandLA-Net-master\results\Log_2024-05-03_09-02-24\snapshots
存放模型的训练参数文件,其中checkpoint文件存放了多次保存的模型参数文件名称。
注意事项:
1、本百度网盘不包含任何点云数据,仅为项目代码;
2、电力档段激光点云数据文件与S3DIS Dataset文件树结构一致,具体的数据文件树结构转换代码详见基于PointNet / PointNet++深度学习模型的激光点云语义分割-CSDN博客;
3、由于点云采样的随机性与最近邻点标签上采样还原机制,点云类别标签预测会在每一次测试中体现出差异,因此设置多次验证取,对每个点取最多次预测的类别标签较为准确;
4、具体的命令行训练以及测试流程依据参考资料[1]的Semantic3D部分。
参考资料:
[1] GitHub - QingyongHu/RandLA-Net: 🔥RandLA-Net in Tensorflow (CVPR 2020, Oral & IEEE TPAMI 2021)
[2] RandLa-Net_哔哩哔哩_bilibili
[3] https://zhuanlan.zhihu.com/p/105433460
[4] 从零开始点云语义分割:RandLANet教程-CSDN博客
[5] https://www.tensorflow.org/api_docs/python/tf
[6] conda虚拟环境中安装cuda和cudnn,再也不用头疼版本号的问题了_conda cudnn-CSDN博客
RandLA-Net发表论文
/*1*/ RandLA-Net
https://arxiv.org/abs/1911.11236
相关文章:

基于RandLA-Net深度学习模型的激光点云语义分割
一、场景要素语义分割部分的文献阅读笔记 RandLA-Net是一种高效、轻量级的神经网络,其可直接逐点推理大规模点云的语义标签。RandLA-Net基于随机点采样获得了显著的计算和内存效率,并采用新的局部特征聚合模块有效地保留了几何细节,弥补了随机…...

C语言的结构体与联合体
引言 C语言提供了结构体和联合体两种聚合数据类型,使得程序员可以创建包括多个数据类型的复杂数据结构。结构体用于将不同类型的数据组合成一个单元,而联合体用于在同一存储空间中存储不同类型的数据。本篇文章将详细介绍C语言中的结构体和联合体&#x…...
_forwardRef)
React Hooks小记(三)_forwardRef
forwardRef 【写在前面】 1、ref 的作用是获取实例,但由于函数组件不存在实例,因此无法通过 ref 获取函数组件的实例引用,而 React.forwardRef 就是用来解决这个问题的。 2、React.forwardRef 会创建一个 React 组件,这个组…...

面试复习记录
六级终于结束了,之前背的八股几乎也忘得差不多了,今天开始继续准备秋招,以下是每天的安排,会按时更新,就当是一种对自己的督促,也欢迎小伙伴们一起来互相监督。 2024.6.16 力扣:sql基础题库50…...

块级元素与行内元素详解
在网页设计与开发中,元素根据其在页面布局中的表现可分为两大类:块级元素(Block-level Elements)和行内元素(Inline Elements)。理解它们的特性和使用规则对于构建结构清晰、布局合理的网页至关重要。 块级…...
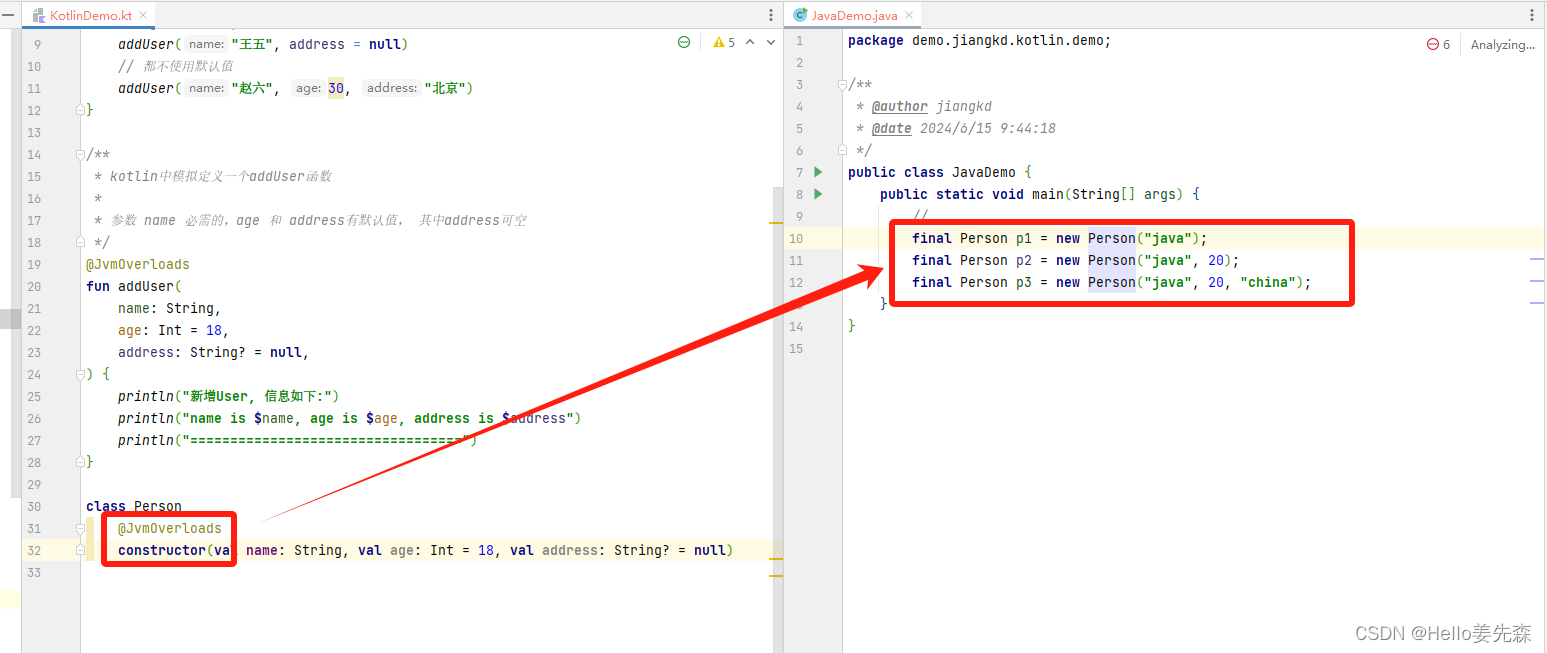
Kotlin编程实践-【Java如何调用Kotlin中带默认值参数的函数】
问题 如果你有一个带有默认参数值的 Kotlin 函数,如何从 Java 调用它而无须为每个参数显式指定值? 方案 为函数添加注解JvmOverloads。 也就是为Java添加重载方法,这样Java调用Kotlin的方法时就不用传递全部的参数了。 示例 在 Kotlin …...
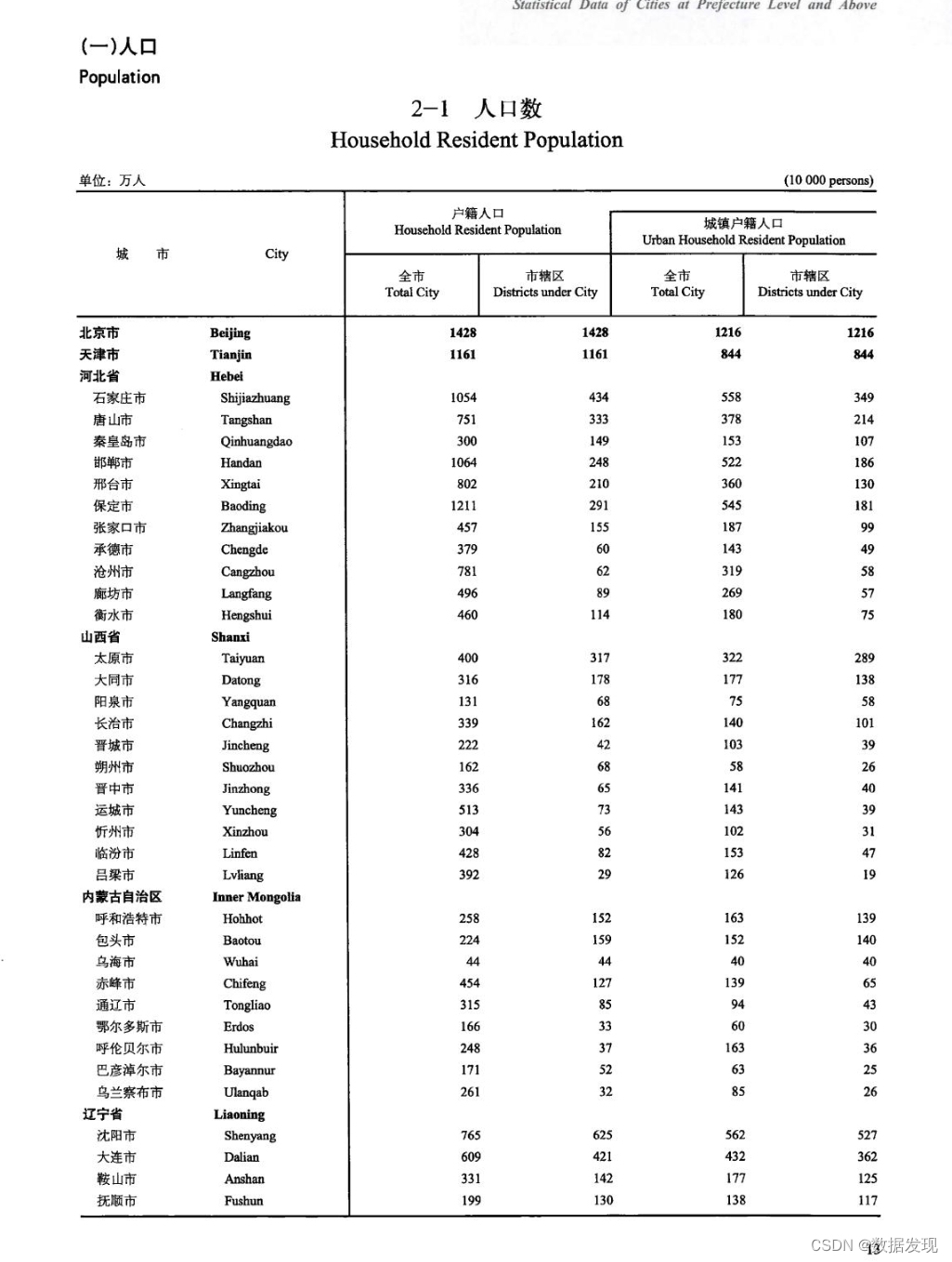
中国城市统计年鉴(1985-2023年)
数据年限:1985-2023 数据格式:pdf、excel 数据内容:共分四个部分 第一部分是全国城市行政区划,列有不同区域、不同级别的城市分布情况; 第二、三部分分别是地级以上城市统计资料和县级城市统计资料,具体包括…...
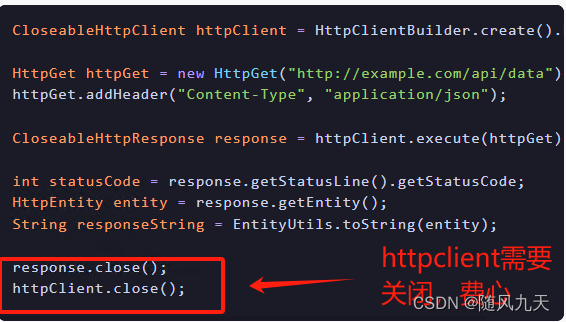
RestTemplate远程请求的艺术
1 简说 编程是一门艺术,追求优雅的代码就像追求优美的音乐。 很多有多年工作经验的开发者,在使用RestTemplate之前常常使用HttpClient,然而接触了RestTemplate之后,却愿意放弃多年相处的“老朋友”,转向RestTemplate。那么一定是RestTemplate有它的魅力,有它的艺术风范。…...
Spring 整合 MyBatis 底层源码解析
大家好,我是柳岸花开。今天我们要讲的是 Spring 整合 MyBatis 的底层源码解析。希望大家能更深入理解 Spring 和 MyBatis 的整合原理,并应用到实际项目中。 由很多框架都需要和Spring进行整合,而整合的核心思想就是把其他框架所产生的对象放到…...

LeetCode 189.轮转数组
1.这个题我用的方法比较巧妙,大家如果觉得好的话,就给个免费的赞吧^ _ ^,谢谢了。 void reverse(int* nums,int left,int right) {while(left < right){int a nums[left];nums[left] nums[right];nums[right] a;left;right--;} } void rotate(int…...

JDK17 你的下一个白月光
JDK版本升级的非常快,现在已经到JDK20了。JDK版本虽多,但应用最广泛的还得是JDK8,正所谓“他发任他发,我用Java8”。 但实际情况却不是这样,越来越多的java工程师拥抱 JDK17,于是了解了一下 JDK17新语法&a…...

springboot优雅shutdown时如何保障异步线程的安全
我前面写了一篇springboot优雅shutdown的文章,看起来一切很美好。 https://blog.csdn.net/chenshm/article/details/139640775 那是因为没有进行多线程测试。如果一个请求中包括阻塞线程(主线程)和非阻塞线程(异步线程)…...

C++格式化库fmt使用方法
1. 格式化库fmt简介 fmt github地址 api说明 格式化参数说明 内容的格式化,体现在代码中主要表现为字符串、基本类型、自定义类型的拼接。例如说打印日志、拼接变量等。C中我们会经常使用类似printf,snprintf(C风格使用不方便),std::string.append(繁琐), std::io…...

HTML 颜色名:网页设计的调色板
HTML 颜色名:网页设计的调色板 在网页设计和开发中,颜色是一个关键元素,它不仅影响视觉效果,还能传达情感和品牌信息。HTML 颜色名是用于在 HTML 和 CSS 代码中指定颜色的预定义名称。这些颜色名易于记忆,方便设计师和开发者快速选择和应用颜色。本文将详细介绍 HTML 颜色…...
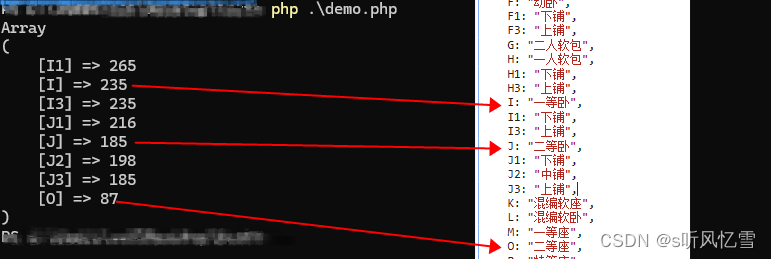
12306 火车票价格解析 (PHP 解析)
1. 从接口拿数据 日期 出发站 终点站 都填上 xxx/otn/leftTicketPrice/queryAllPublicPrice?leftTicketDTO.train_date2024-06-15&leftTicketDTO.from_stationBJP&leftTicketDTO.to_stationSJP&purpose_codesADULT 返回的数据是这样的 {"validateMess…...

了解统计学中不同类型的分布
目录 一、说明 二、均匀分布: 三、机器学习和数据科学中的均匀分布示例: 3.1 对数正态分布: 3.2 机器学习和数据科学中的对数正态分布示例: 四、 帕累托分布 4.1 什么是幂律? 4.2 机器学习和数据科学中的帕累托分布示例…...

k8s-CCE创建工作负载变量引用
CCE创建工作负载变量引用 背景,看到cce创建负载时会生成变量,如下。在skywaking-agent的使用,想要调用cce负载变量生成service_name。 -Dskywalking.agent.authentication里含有敏感信息需要写到配置项。简单粗糙的都写到配置项好像不合适。…...

后端主流框架--Spring02
前言:上篇关于Spring的文章介绍了一些Spring的基本知识,此篇文章主要分享一下如何配置Spring环境,如何注入等。 Spring项目构建 导入Spring相关JAR包 <dependency><groupId>org.springframework</groupId><artifactId>spring…...

[数据集][目标检测]减速带检测数据集VOC+YOLO格式5400张1类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):5400 标注数量(xml文件个数):5400 标注数量(txt文件个数):5400 标注…...

分析Linux操作指令及使用场景与频率分析 持续更新
本篇主要针对在日常工作与学习中使用较多的linux指令的使用方法以及使用频次进行分析与讲解,旨在能够更好的掌握这些必备的技能。 linux指令非常的多,如果要记住所有的指令使用方法是非常困难的且要花费很长的时间,很多人习惯离开使用去通篇…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
