Python | 中心极限定理介绍及实现
统计学是数据科学项目的重要组成部分。每当我们想从数据集的样本中对数据集的总体进行任何推断,从数据集中收集信息,或者对数据集的参数进行任何假设时,我们都会使用统计工具。
中心极限定理
定义:中心极限定理,通俗地来说,就是研究独立随机变量和的极限分布为正态分布的问题。在自然界和生产中,许多现象受到许多相互独立的随机因素的影响。当每个因素的影响都很微小时,这些因素产生的总影响可以看作是服从正态分布的。中心极限定理就是从数学上证明了这一现象。
具体来说,中心极限定理表明,无论随机变量的初始分布是什么,只要我们对这些随机变量进行大量的独立抽取,并将这些随机变量加起来,那么这些总和的分布就会接近正态分布。这种规律在我们的生活中也随处可见,比如人的身高、体重等数据的分布都近似于正态分布。
举个例子:
假设有一个班级,其中学生的成绩是随机变量,每个学生都是一个独立的随机变量。如果我们把所有学生的成绩加起来,并计算平均分,那么这个平均分的分布就会接近正态分布。
具体来说,我们可以将每个学生的成绩看作是一个独立的随机变量,每个随机变量都有自己的分布。如果我们把所有学生的成绩加起来,那么这个总和就是一个随机变量。根据中心极限定理,这个总和的分布就会接近正态分布。
这个例子可以用来解释为什么大多数情况下,班级的平均分分布会呈现出一个类似于正态分布的形状。这是因为每个学生的成绩都是独立的随机变量,而这些随机变量的总和近似于正态分布。
应用场景
中心极限定理在数理统计和概率论中有着广泛的应用,主要包括以下几个方面:
- 验证数据是否满足正态分布:如果数据符合正态分布的条件,则可以使用相关的统计方法进行分析。而如果数据不符合正态分布的条件,就需要采用其他的统计方法进行分析。
- 求解总体参数:中心极限定理可以用于求解总体的均值和方差等参数。通过对样本进行一些简单的统计分析,就可以根据中心极限定理的推导,得到总体的均值和方差等参数的近似值。
- 构造置信区间:当对总体参数进行估计时,可以使用中心极限定理的知识,构造置信区间进行区间估计,从而提高估计的可靠性。
- 应用于大样本:在处理大样本时,中心极限定理是非常重要的工具。它能够证明在样本容量足够大的情况下,样本均值的分布近似于正态分布,从而可以应用正态分布的统计性质进行各种统计推断。
- 解决实际问题:中心极限定理可以用于解决许多实际问题,例如金融领域中的风险评估、医学领域中的临床试验、生产制造中的质量控制等。在这些领域中,中心极限定理可以帮助我们理解数据的分布规律,并进行更准确的预测和决策。
总之,中心极限定理是概率论中的一组非常重要的定理,它揭示了大量随机变量之和的分布规律,并广泛应用于数理统计学、误差分析、自然与生产现象的解释等领域。在实际应用中,它可以用于验证数据的分布、求解总体参数、构造置信区间、应用于大样本以及解决各种实际问题。
中心极限定理的Python实现
import numpy
import matplotlib.pyplot as plt# number of sample
num = [1, 10, 50, 100]
# list of sample means
means = [] # Generating 1, 10, 30, 100 random numbers from -40 to 40
# taking their mean and appending it to list means.
for j in num:# Generating seed so that we can get same result # every time the loop is run...numpy.random.seed(1)x = [numpy.mean(numpy.random.randint(-40, 40, j)) for _i in range(1000)]means.append(x)
k = 0# plotting all the means in one figure
fig, ax = plt.subplots(2, 2, figsize =(8, 8))
for i in range(0, 2):for j in range(0, 2):# Histogram for each x stored in meansax[i, j].hist(means[k], 10, density = True)ax[i, j].set_title(label = num[k])k = k + 1
plt.show()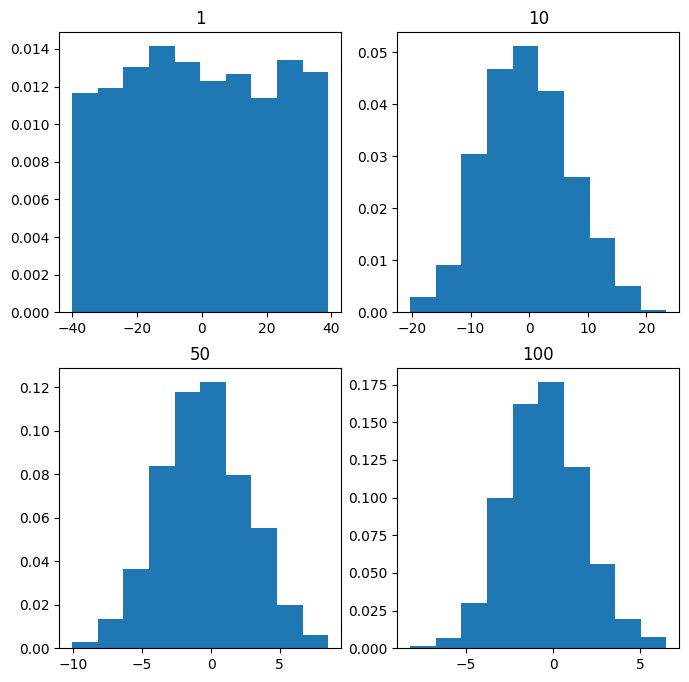
从图中可以明显看出,随着样本量从1增加到100,直方图趋于正态分布。
中心极限定理的经验法则
中心极限定理的经验法则是指在实际应用中,如果随机变量足够多,那么这些随机变量之和的分布近似于正态分布。这个经验法则在数理统计学和误差分析中非常重要,可以用来解决各种实际问题。
例如,在金融领域中,中心极限定理的经验法则可以用来评估投资组合的风险。通过将大量的股票价格看作是随机变量,并计算它们的均值和方差,就可以得到投资组合的收益率分布。由于这些随机变量足够多,它们的分布近似于正态分布,因此可以使用正态分布的性质来计算投资组合的风险。
在生产制造中,中心极限定理的经验法则可以用来控制产品质量。通过对生产过程中产生的大量数据进行分析,可以计算出这些数据的均值和方差,并根据中心极限定理的推导,得到这些数据的分布近似于正态分布。因此,可以根据正态分布的性质制定控制限,控制产品质量,提高生产效率。
总之,中心极限定理的经验法则是数理统计学和误差分析中非常重要的一个工具,可以用来解决各种实际问题。在实际应用中,只要随机变量足够多,它们的分布就可以近似地看作是正态分布,从而可以使用正态分布的性质进行各种统计推断。
相关文章:

Python | 中心极限定理介绍及实现
统计学是数据科学项目的重要组成部分。每当我们想从数据集的样本中对数据集的总体进行任何推断,从数据集中收集信息,或者对数据集的参数进行任何假设时,我们都会使用统计工具。 中心极限定理 定义:中心极限定理,通俗…...
探索Napier:Kotlin Multiplatform的日志记录库
探索Napier:Kotlin Multiplatform的日志记录库 在现代软件开发中,日志记录是不可或缺的部分,它帮助开发者追踪应用的行为和调试问题。对于Kotlin Multiplatform项目而言,能够在多个平台上统一日志记录的方法显得尤为重要。Napier…...

MySQL基础——SQL语句
目录 1.SQL通用语法 2.SQL分类 3 DDL 3.1数据库操作 3.1.1查询 3.1.2创建 3.1.3删除 3.1.4使用 3.2表操作 3.2.1查询 3.2.2创建 3.2.3数据类型 3.2.4表修改(alter打头) 3.2.5表删除(drop/truncate打头) 3.3 DDL总结…...

比特币通用API服务
Bitcoin 通用API服务 exlectrs: API后台服务(Rust语言编写) https://github.com/Blockstream/electrs.git 使用electr作为后台的区块链浏览器:https://github.com/Blockstream/esplora.git https://github.com/Blockstream/electrs https://github.com/romanz/electrs/blo…...

Spock mock私有方法
mock私有方法 被测试的方法是MiddleGroundAppListBO类下的getPromptIdKeyAppPromptInfoMap方法 private Map<Long, AppPromptInfoModel> getPromptIdKeyAppPromptInfoMap(String cubeAppIdentity) {List<AppPromptInfoDO> promptByApp knowledgeCubeQueryR…...

网络协议四
一、云中网络 物理机的劣势: 1)一旦需要扩容 CPU、内存、硬盘,都需要去机房手动弄,非常麻烦 2)采购的机器往往动不动几百 G 的内存,而每个应用往往可能只需要 4 核 8G 3)一台机器,…...

大数据入门实践一:mac安装Hadoop,Hbase,FLume
一、安装Hadoop 安装hadoop参考此文,关键点是安装JDK和Hadoop的配置,为避免引用文章变收费,我把关键信息摘录如下: jdk安装和配置就不说了(我本机安装了1.8/15/17/21,以17为主),hadoop安装过程…...
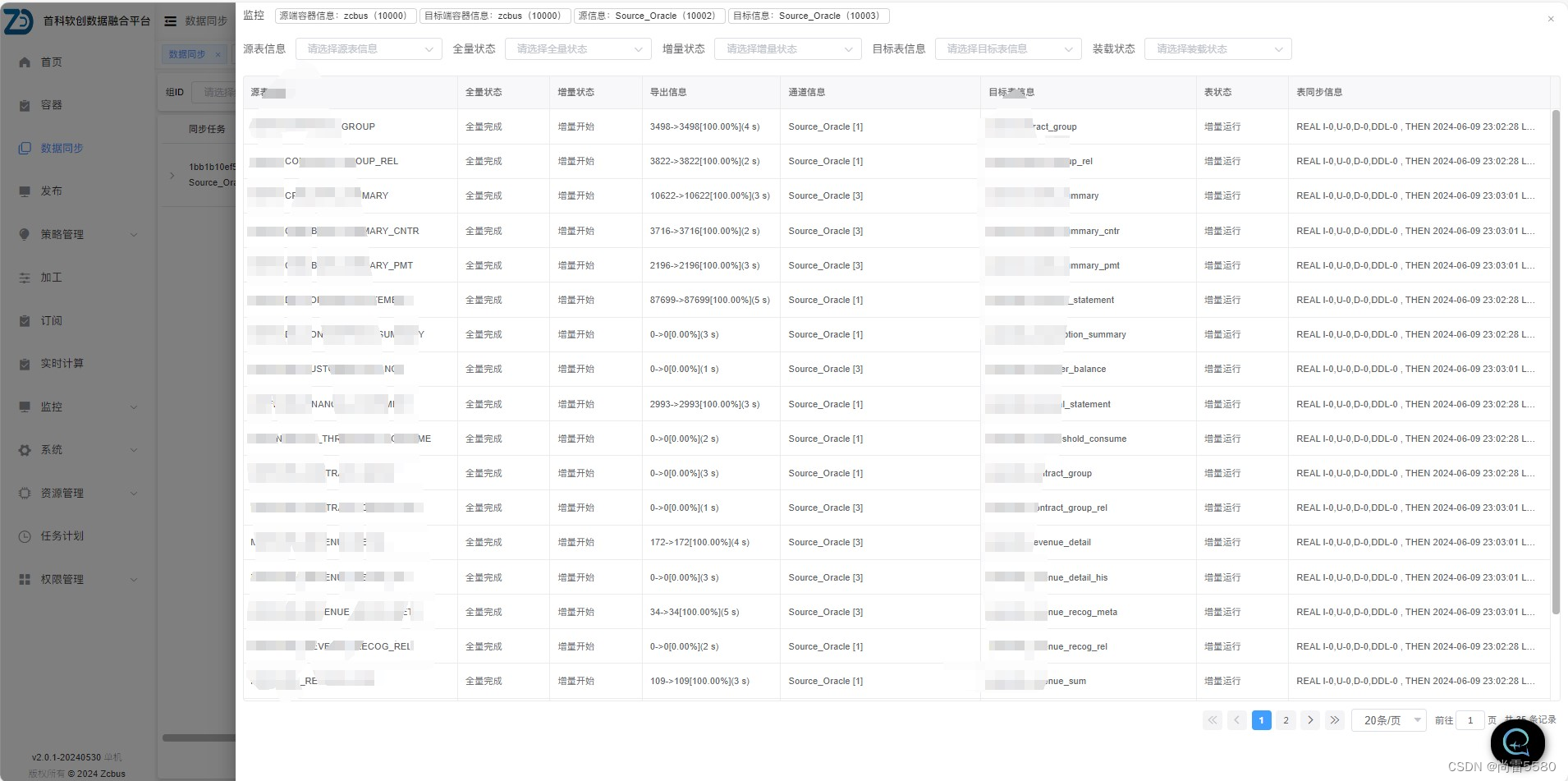
openGauss 6.0.0 一主二备集群安装及使用zcbus实现Oracle到openGauss的数据同步
一、前言 openGauss 6.0.0-RC1是openGauss 2024年3月发布的创新版本,该版本生命周期为0.5年。根据openGauss官网介绍,6.0.0-RC1与之前的版本特性功能保持兼容,另外,在和之前版本兼容的基础上增加了很多新功能,比如分区表性能优化…...

0118__C语言——float.h文件
C语言——float.h文件_c float.h-CSDN博客...

settings和toolchains.xml 区别用法配置
在 IntelliJ IDEA 中配置 Maven 项目时,settings.xml 和 toolchains.xml 的使用场景有所不同。以下是具体的使用情景和配置方法: 1. 使用 settings.xml 使用场景 全局或用户级别的配置:包括设置本地仓库位置、远程仓库、代理服务器、认证信…...
、416. 分割等和子集)
leetcode打卡#day43 携带研究材料(第六期模拟笔试)、416. 分割等和子集
携带研究材料(第六期模拟笔试) #include<iostream> #include<algorithm> #include<vector>using namespace std;int getMaxValue(vector<int>& weights, vector<int>& values, int n, int m) {vector<vector&…...

MPLS的配置
1、IP可达--- 使用路由协议全网可达 2、配置 MPLS ——LDP [r2]mpls lsr-id 2.2.2.2 必须先定义 mpls 的router-id,要为本地设备的真实ip地址,且邻居可达,因为该地址将用于建立 TCP 会话,建议使用环回地址 [r2]mpls 再开…...

【机器学习】机器学习与教育科技在个性化教学中的融合应用与性能优化新探索
文章目录 引言机器学习与教育科技的基本概念机器学习概述监督学习无监督学习强化学习 教育科技概述学生学习行为分析个性化学习路径推荐智能化教育评估 机器学习与教育科技的融合应用实时学习数据分析数据预处理特征工程 学生成绩预测与优化模型训练模型评估 个性化学习路径推荐…...

C++:十大排序
目录 时间复杂度分析 选择排序 引言 算法思想 动图展示 代码实现 (升序) 优化 代码实现 分析 冒泡排序 引言 算法思想 动图展示 代码实现 插入排序 引言 算法思想 动图展示 代码实现 计数排序 引言 算法思想 动图展示 代码实现 桶排序 引言 算法思…...
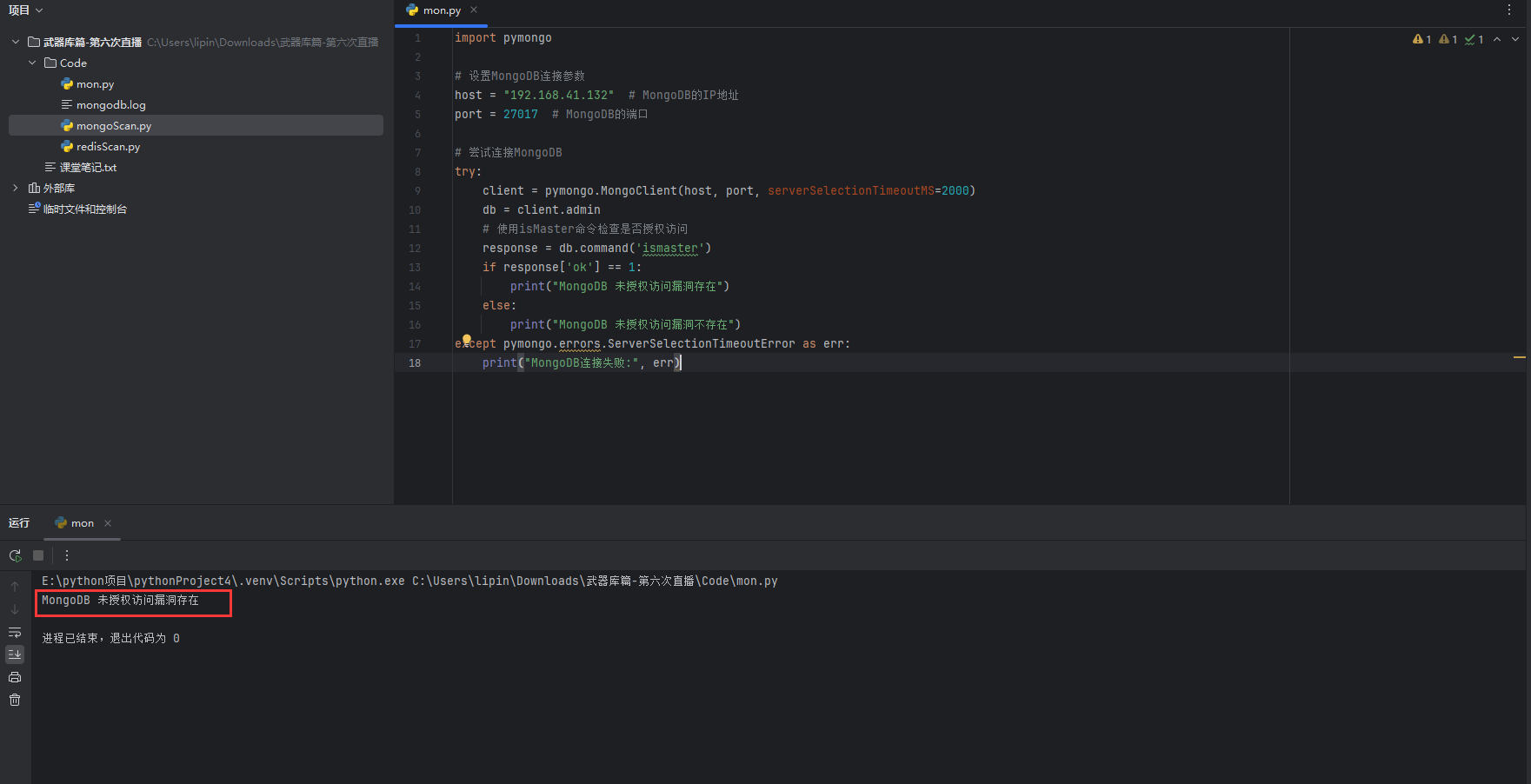
Python武器库开发-武器库篇之Mongodb未授权漏洞扫描器(五十六)
Python武器库开发-武器库篇之Mongodb未授权漏洞扫描器(五十六) MongoDB 未授权访问漏洞简介以及危害 MongoDB是一款非常受欢迎的开源NoSQL数据库,广泛应用于各种Web应用和移动应用中。然而,由于默认配置的不当或者管理员的疏忽,导致不少Mon…...

【论文速读,找找启发点】2024/6/16
ICME 2023 End-To-End Part-Level Action Parsing With Transformer 类似 DETR,通过 加 query的方式实现 端到端 ELAN: Enhancing Temporal Action Detection with Location Awareness 如何实现位置感知? > 重叠的卷积核? Do we really …...

canal监控mysql变化
目录 概述实践代码总结表创建插入一行数据更新一行数据删除一笔数据 概述 本文测试 canal 监控 mysql 表变化。canal 1.1.7 mysql 8.0.x 版本。 实践 代码 public static void main(String[] args) {// 创建一个 CanalConnector 连接器// username:字符串类型,Canal使用该用…...
MySQLWorkbench导出sql文件
MySQLWorkbench导出sql文件 前言效果图导出操作选择要导出的数据库遇到的问题解决问题 查看mysql路径 前言 在完成数据库搭建之后,需要为上线做准备,那么就需要导出数据库的建库sql了 本篇文章讲解的是mysql Workbench 导出数据建库脚本 效果图 导出操…...

不一样的SYSTEM APP(SYSTEM flag和system_prop区别)
1.问题引入 在Android开发中, 1)Framework中PackageManager扫包后,会把app归类为SYSTEM, SYSTEM_EXT, PRIVILEGED 类别. 2)同样的, SeAndroid也会把APP归类程platform_app, system_app, untrusted_app(甚至还有其他,mediaprovider,gmscore_app). flag SYSTEM和system_app我们…...
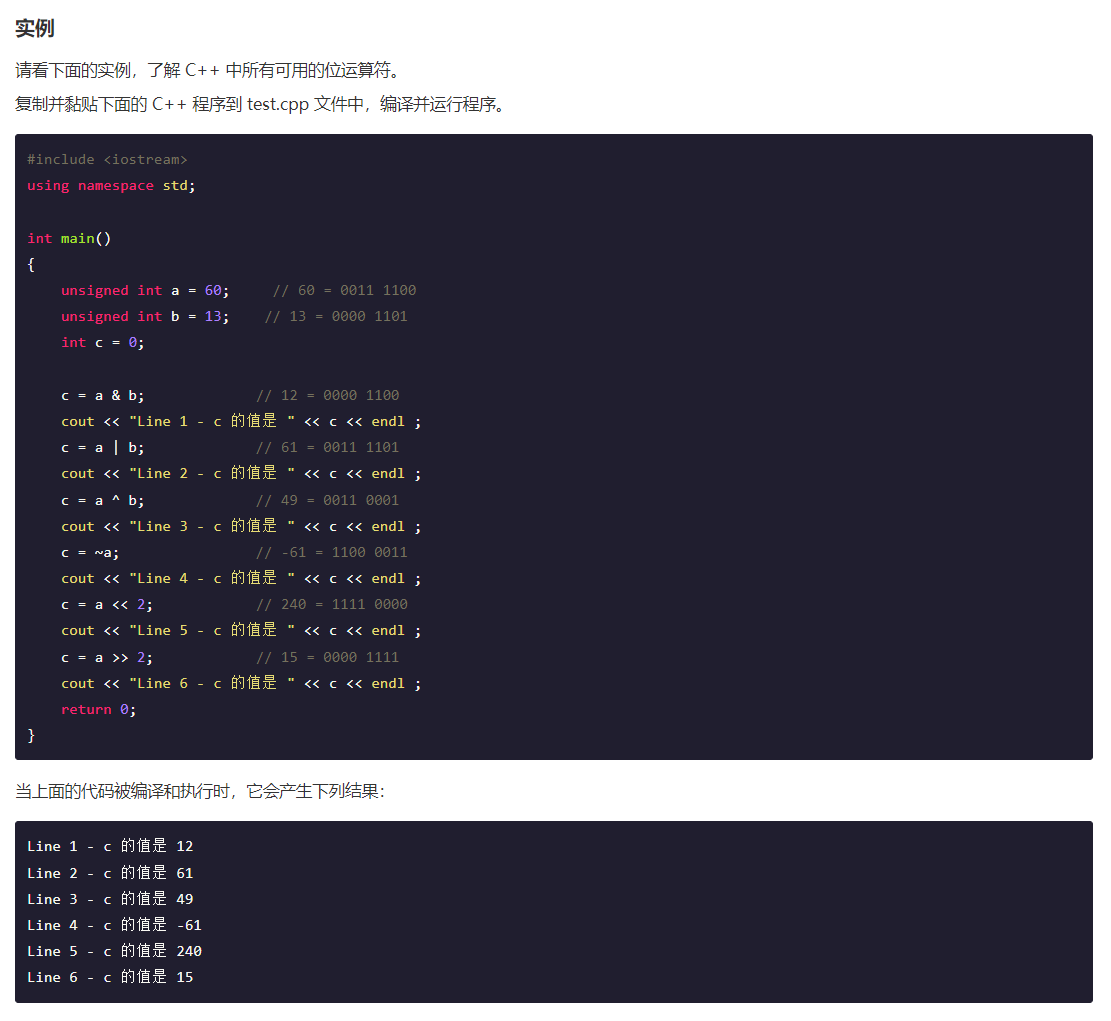
C++ 和 JAVA 位运算符
C 和 JAVA 位运算符...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
