【数据结构】堆排序
堆是一种叫做完全二叉树的数据结构,可以分为大根堆,小根堆,而堆排序就是基于这种结构而产生的一种程序算法。
大堆:每个节点的值都大于或者等于他的左右孩子节点的值
小堆:每个结点的值都小于或等于其左孩子和右孩子结点的值
不管是大堆还是小堆父节点的数组下标和其孩子节点的下标关系都为
parent=(child-1)/2 leftchild=2*parent+1 rightchild=2*parent+2
建堆
建堆有两种方法1.向上调整建堆2.向下调整建堆
向上调整建堆
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustUp(int* a, int child) //向上调整
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]) //建大堆还是小堆在这里调整{ //大堆a[parent]<a[child] 小堆反之Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HeapSort(int* a, int n)
{for (int i = 0; i < n; ++i){AdjustUp(a, i);}
}int main()
{int a[] = { 1,10,2,20,3,30,4,40,5,50 };HeapSort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); ++i){printf("%d ", a[i]);}return 0;
}
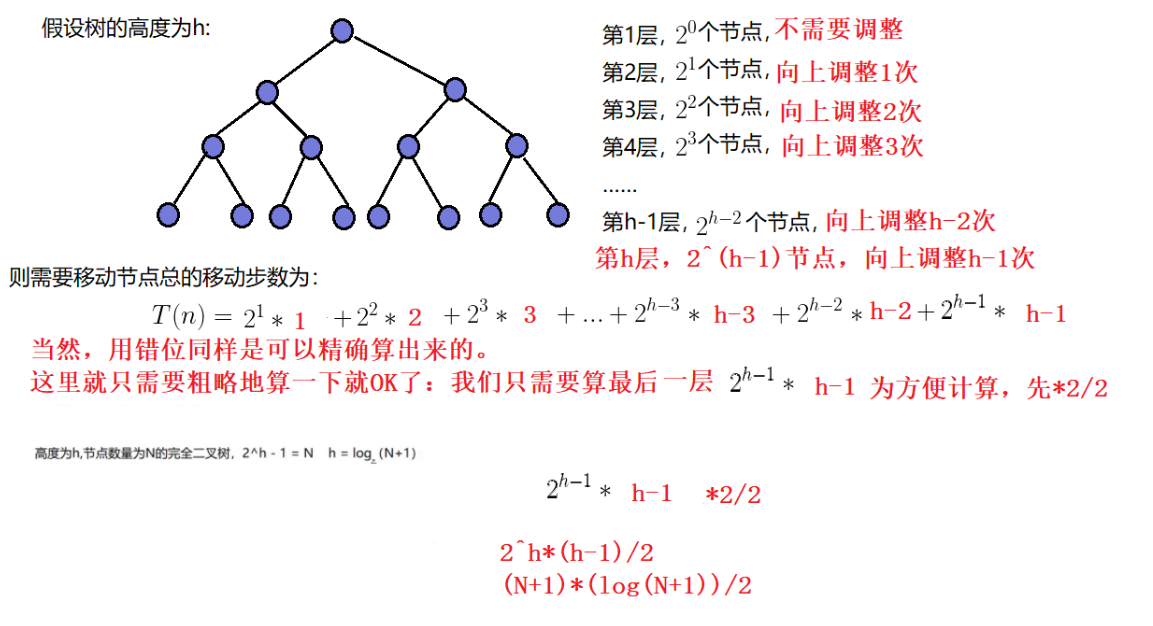
向上调整建堆是从数组的第一个元素开始一次向后遍历数组元素,每一个数组元素都向上调整建堆,这个过程就模拟建立起了堆,这个过程的时间复杂度推导过程:O(N*logN)
2.向下调整建堆(推荐使用)
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustDown(int* a, int n, int parent) //向下调整
{int minChild = parent * 2 + 1;while (minChild < n){if (minChild + 1 < n && a[minChild + 1] > a[minChild]) //这里控制大小堆{minChild++;}if (a[minChild] > a[parent]) //这里控制大小堆{Swap(&a[minChild], &a[parent]);parent = minChild;minChild = parent * 2 + 1;}else{break;}}}
void HeapSort(int* a, int n)
{for (int i = (n - 1-1) / 2; i >= 0; --i){AdjustDown(a, n, i);}
}int main()
{int a[] = { 1,10,2,20,3,30,4,40,5,50 };HeapSort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); ++i){printf("%d ", a[i]);}return 0;
}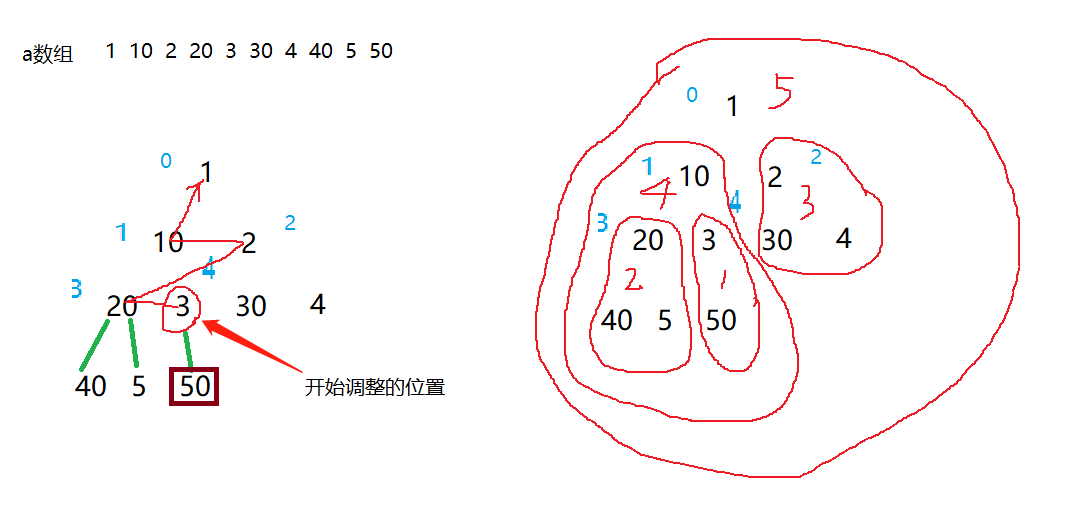
向下调整的开始的位置是最后一个元素的父节点位置,因为最后一行的元素本来就符合大堆或者小堆的性质所以不用调整,根据数组的最后一个元素的下标计算出该节点的父节点的数组下标,从这个父节点开始向下调整,调整完后再将父节点的数组下标--,再从这个节点开始向下调整,直到调整完根节点后调整结束,堆就建立好了,大小堆是根据向下调整函数里的比较决定的。时间复杂度推导如下O(N):
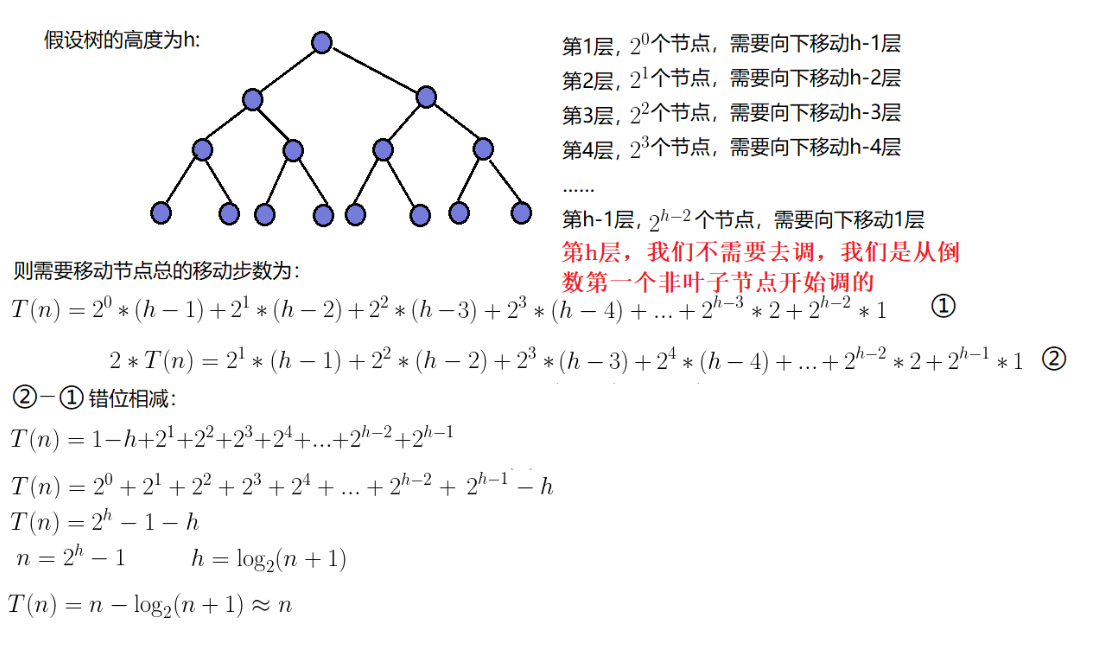
因为向下调整的时间复杂度低于向上调整的时间复杂度,所以推荐使用的是向下调整建堆。
2.选数
了解完以后,我们来实现堆排序:
void AdjustDown(HPDataType* a, int n, int parent)
{//最小的默认为左孩子int minchild = 2 * parent + 1;while (minchild <n){//找出小的那个孩子if (minchild+1<n&&a[minchild+1] < a[minchild]){minchild++;}//小堆if (a[minchild] < a[parent]){Swap(&a[minchild], &a[parent]);parent = minchild;minchild = 2 * parent + 1;}else{break;}}
}void HeapSort(int* a, int n)
{for (int i = (n-1-1)/2; i>=0; i--){AdjustDown(a, n, i);}//选数int i = 1;while (i < n){Swap(&a[0], &a[n - i]);AdjustDown(a, n - i, 0);i++;}}int main()
{int a[] = { 15,1,19,25,8,34,65,4,27,7 };HeapSort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); i++){printf("%d ", a[i]);}printf("\n");return 0;
}
这里的思路就是先对数组进行向下调整建堆,如果要升序就建立大堆,将根节点位置的元素和最后一个元素交换位置使得最大的元素放到了数组的最后边,放到后边的元素不参与向下调整(通过传参控制),然后让被换到根节点的元素向下调整,回到符合堆的性质的位置,此时调整完成后次大的元素被调整到了根节点的位置,再让根节点的元素和倒数第二个元素交换,交换到后边的元素不参与向下调整,再次进行向下调整,直到i=n时结束调整,此时输出数组就是升序的。如果要降序那就建立小堆。
总结一句话:
升序--建大堆,降序--建小堆
3.TOP-K问题
如何从数组中找到前K个大或者前K个小的数?
错误的思维:
选前K个大的数建立的是大堆,那最大的元素就在最上方,我们拿走了最大的元素,那剩下的元素堆的关系全乱了,又得重新排序,再选出最大的元素,这样一来假设要从特别大的一堆数据中进行选数那代价就非常大了,效率变得很低。同理选小数不能建小堆。
正确方法:
用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
代码实现:
#include<stdlib.h>
#include<stdio.h>void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustDown(int* a, int n, int parent) //向下调整
{int minChild = parent * 2 + 1;while (minChild < n){if (minChild + 1 < n && a[minChild + 1] < a[minChild]){minChild++;}if (a[minChild] < a[parent]){Swap(&a[minChild], &a[parent]);parent = minChild;minChild = parent * 2 + 1;}else{break;}}}
void Topk(int* a, int k,int n)
{int* minheap = (int*)malloc(k * sizeof(int));if (minheap == NULL){perror("malloc fail!");exit(-1);}for (int i = 0; i < k; i++){minheap[i] = a[i];}for (int j = (k - 2) / 2; j >= 0; --j){AdjustDown(minheap, k, j); //向下调整建小堆因为选的是前K大的数 ---如果选小数就建大堆}int k1 = k;//遍历k后的元素交换然后调整while (k <n){if (a[k] > minheap[0]){minheap[0] = a[k];AdjustDown(minheap, k, 0);}++k;}for (int i = 0; i < k1; ++i){printf("%d ", minheap[i]);}}
int main()
{int a[] = { 1,10,2,20,3,30,4,40,5,50 };int k = 5; //选出前5个大的数int n = sizeof(a) / sizeof(int); //数组元素个数Topk(a, k,n);return 0;
}
相关文章:

【数据结构】堆排序
堆是一种叫做完全二叉树的数据结构,可以分为大根堆,小根堆,而堆排序就是基于这种结构而产生的一种程序算法。大堆:每个节点的值都大于或者等于他的左右孩子节点的值小堆:每个结点的值都小于或等于其左孩子和右孩子结点…...
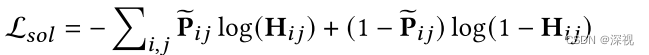
论文阅读笔记《GAMnet: Robust Feature Matching via Graph Adversarial-Matching Network》
核心思想 本文提出一种基于图对抗神经网络的图匹配算法(GAMnet),使用图神经网络作为生成器分别生成源图和目标图的节点的特征,并用一个多层感知机作为辨别器来区分两个特征是否来自同一个图,通过对抗训练的办法提高生成器特征提取…...

数据安全—数据完整性校验
1、数据安全保障三要素即 保密性 完整性、可用性机密性:要求数据不被他人轻易获取,需要进行数据加密。完整性:要求数据不被他人随意修改,需要进行签名技术可用性:要求服务不被他人恶意攻击,需要进行数据校验…...
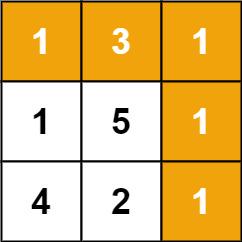
Java 最小路径和
最小路径和中等给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:每次只能向下或者向右移动一步。示例 1:输入:grid [[1,3,1],[1,5,1],[4,2,1]]输出&…...
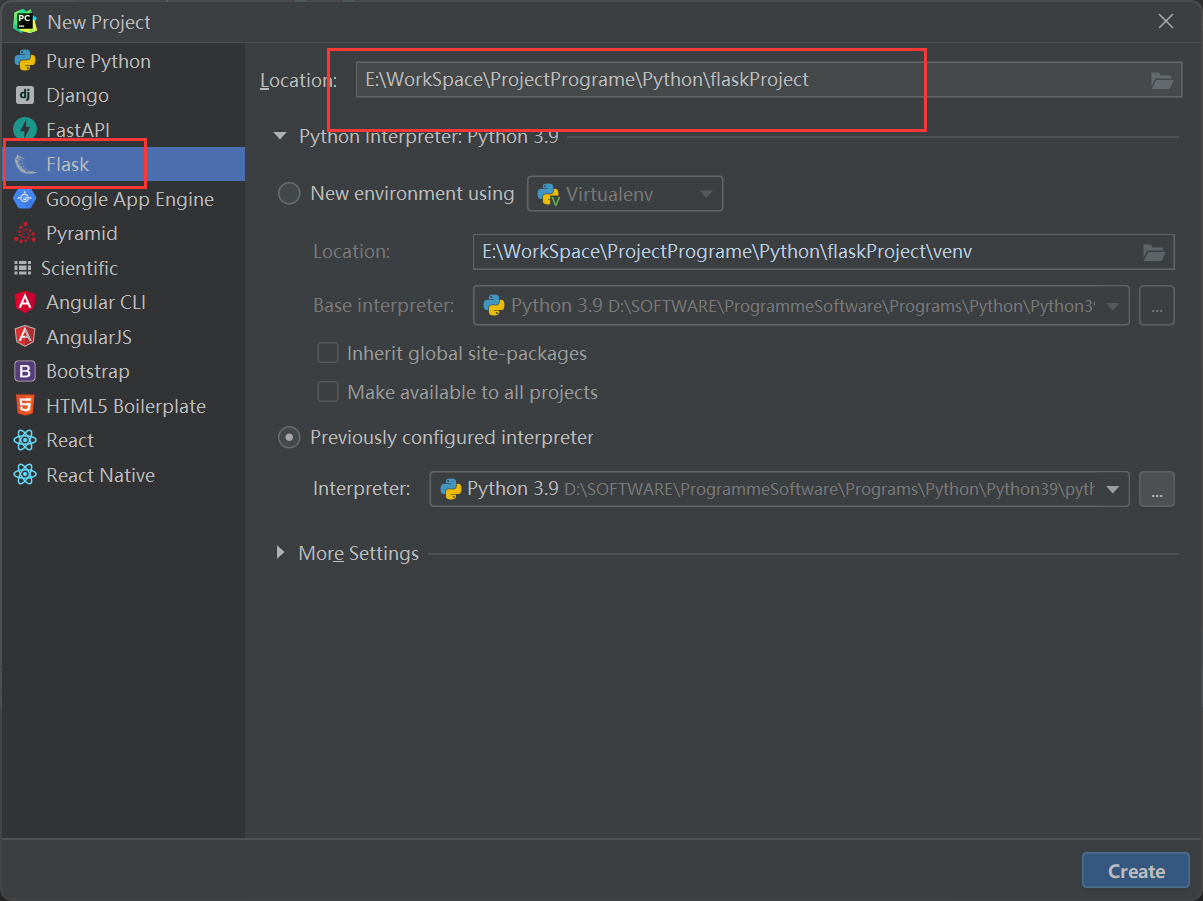
Flask+VUE前后端分离的登入注册系统实现
首先Pycharm创建一个Flask项目: Flask连接数据库需要下载的包: pip install -U flask-cors pip install flask-sqlalchemy Flask 连接和操作Mysql数据库 - 王滚滚啊 - 博客园 (cnblogs.com) sqlAlchemy基本使用 - 简书 (jianshu.com) FlaskVue前后端分…...
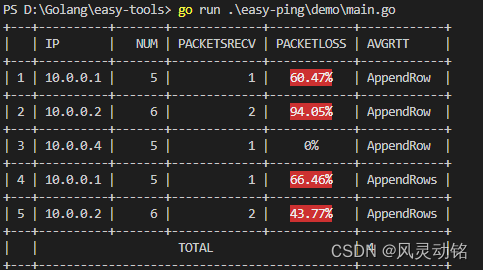
【Go】用Go在命令行输出好看的表格
用Go在命令行输出好看的表格前言正文生成Table表头设置插入行表格标题自动标号单元格合并列合并行合并样式设置居中设置数字自动高亮标红完整Demo代码结语前言 最近在写一些运维小工具,比如批量进行ping包的工具,实现不困难,反正就是ping&am…...

怎么处理消息重发的问题?
消息队列在消息传递的过程中,如果出现传递失败的情况,发送方会重试,在重试的过程中,可能会产生重复的消息。 消息重复的情况必然存在 关于传递消息时能够提供的服务质量标准,MQTT协议给出了三种不同的标准࿱…...
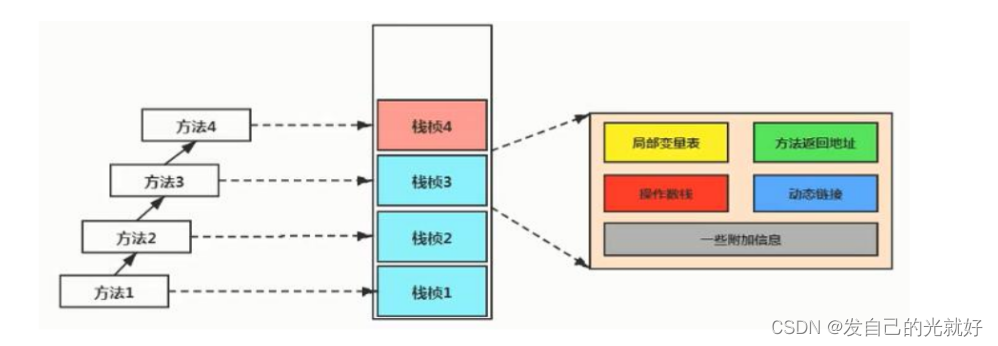
JVM 运行时数据区(数据区组成表述,程序计数器,java虚拟机栈,本地方法栈)
JVM 运行时数据区JVM 运行时数据区3.1运行时的数据区组成概述3.1.1程度计数器3.1.2java虚拟机栈3.1.3本地方法栈3.1.4java堆3.1.5方法区3.2程序计数器3.3java虚拟机栈3.4本地方法栈JVM 运行时数据区 堆,方法区(元空间) 主要用来存放数据 是线程共享的. 程序计数器,本地方法栈…...

Oracle ASM磁盘组配置、日常运维、故障处理等操作资料汇总
ASM(自动存储管理)在数据库中是非常重要的组成部分,它可以为磁盘提供统一的存储管理、提高磁盘访问的性能和可用性、简化管理复杂度,从而为数据库的运行提供更好的支持。这里就为大家整理了墨天轮数据社区上一些ASM相关基础知识、…...
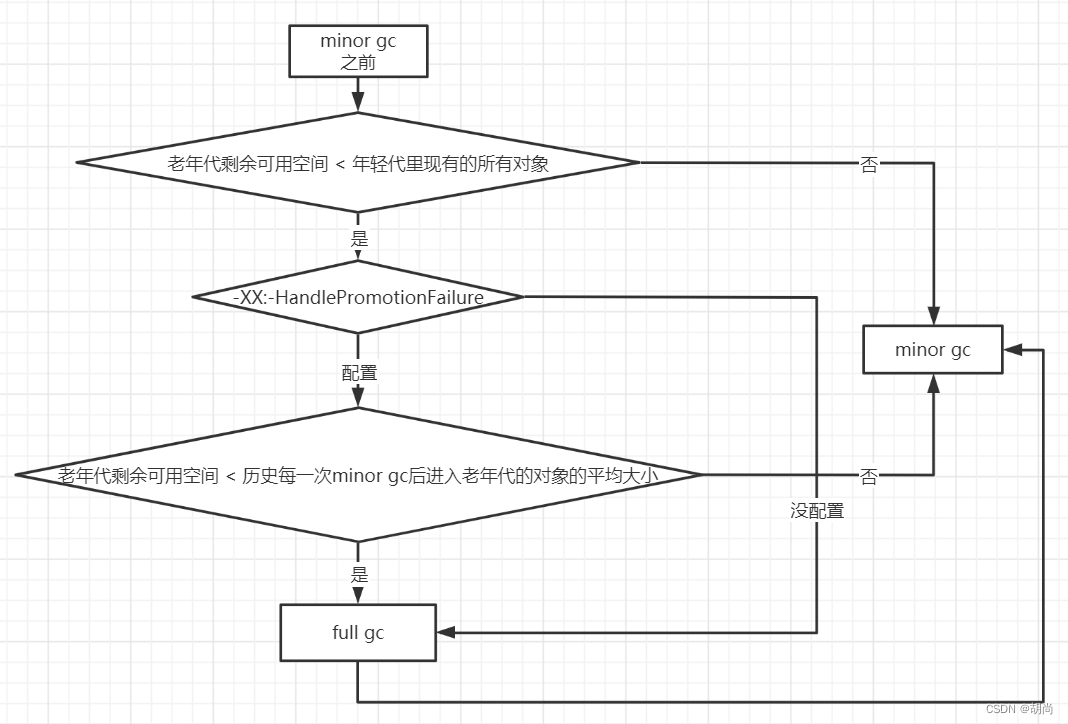
java对象的创建与内存分配机制
文章目录对象的创建与内存分配机制对象的创建类加载检查分配内存初始化零值设置对象头指向init方法其他:指针压缩对象内存分配对象在栈上分配对象在Eden区中分配大对象直接分配到老年代长期存活的对象进入老年代对象动态年龄判断老年代空间分配担保机制对象的内存回…...
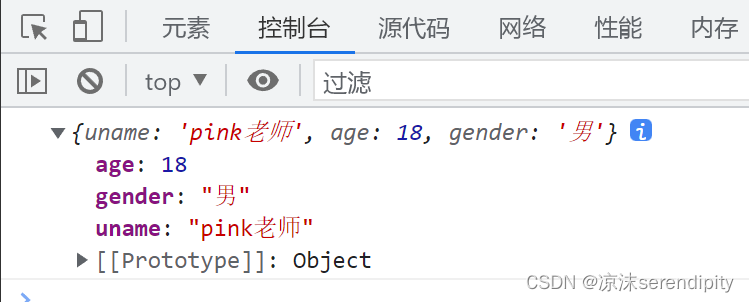
本地存储localStorage、sessionStorage
目录 一、localStorage 二、sessionStorage 三、本地存储处理复杂数据 一、localStorage 介绍 (1)数据存储在用户浏览器中 (2)设置、读取方便、甚至页面刷新不会丢失数据 (3)容量较大,se…...

JavaSE: 网络编程
1.1 概述java程序员面对统一的网络编程环境B/S 架构 和 C/S架构1.2 网络通信的两个要素通信双方的地址:ip 端口号网络通信协议:TCP/IP协议(事实上的国际规则)、OSI模型(理想化)1.3 Inet Address本地回环地…...

计算机图形学09:二维观察之点的裁剪
作者:非妃是公主 专栏:《计算机图形学》 博客地址:https://blog.csdn.net/myf_666 个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩 文章目录专栏推荐专栏系列文章序一、二维观察基本…...

2023Java 并发编程面试题
Java 并发编程 1、在 java 中守护线程和本地线程区别? java 中的线程分为两种:守护线程(Daemon)和用户线程(User)。任何线程都可以设置为守护线程和用户线程,通过方法Thread.setDaemon(boolon…...
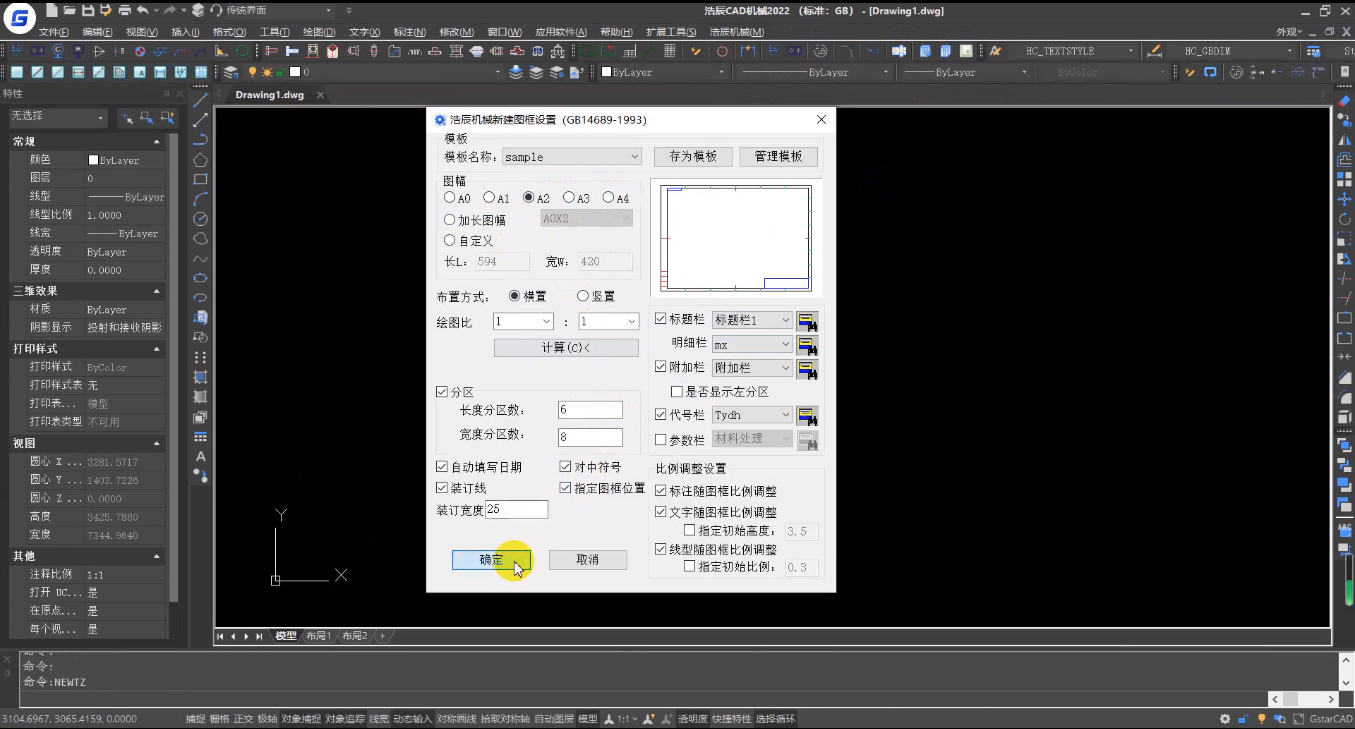
CAD如何绘制A0/A1/A2/A3/A4图框?
在CAD制图时,设计师一般会使用企业的定制图框模板或者个人的特色图框模板,让设计方案更加标准化、规范化。对于新人设计师而言,完成CAD制图已经非常头疼了,图框的绘制更是手忙脚乱。那么是否有更加高效的方式来完成A0、A1、A2、A3…...

R 安装 “umap-learn“ python 包
首先需要在R中下载并读取reticulate包,该包提供了一系列R-Python的交互式命令由于之前在电脑中通过三个方式安装了Python:直接安装 Python 3.10安装Anaconda,携带3.9安装 Miniconda,又是另外一个版本的Python版本各不相同…...

测试同学如何快速开发测试平台?
转眼已经好几个月没有发表什么文章了,因为疫情原因,大家工作都不怎么顺利,没有什么心情。再者,最近一直在搞移动端精准测试的项目,有太多技术难点需要攻克。从各个网站上都找不到解决方案,只能不断地尝试&a…...

【程序员接口百宝箱】免费常用API接口
一、短信发送 短信的应用可以说是非常的广泛了,短信API也是当下非常热门的API~ 短信验证码:可用于登录、注册、找回密码、支付认证等等应用场景。支持三大运营商,3秒可达,99.99%到达率,支持大容量高并发。…...

使数组和能被P整除[同余定理+同余定理变形]
同余定理同余定理变形前言一、使数组和能被P整除二、同余定理变形总结参考资料前言 同余定理非常经典,采用前缀和 map,当两个余数前缀和为一个值时,则中间一段子数组刚好对P整除。但是能否找到前面是否有一段子数组和可以对P整除呐…...

25k的Java开发常问的Synchronized问题有哪些?
前言:面试高频的Synchronized问题大多集中在应用场景、底层实现原理、锁的升级过程。 文章目录 Synchronized定义应用场景对象加锁实现原理JDK6以前JDK6版本及以后对象从无锁到偏向锁转化的过程(大概讲五分钟)轻量级锁升级的过程(大概讲五分钟)自旋锁策略(大概讲五分钟)…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...
