【数学】什么是最大似然估计?如何求解最大似然估计
背景
最大似然估计(Maximum Likelihood Estimation, MLE)是一种估计统计模型参数的方法。它在众多统计学领域中被广泛使用,比如回归分析、时间序列分析、机器学习和经济学。其核心思想是:给定一个观测数据集,找到一组参数,使得在这些参数下观测到当前数据的可能性(似然)最大。
公式
假设我们有一个参数为 θ \theta θ 的概率分布,观测数据为 X = ( x 1 , x 2 , … , x n ) X = (x_1, x_2, \ldots, x_n) X=(x1,x2,…,xn),则似然函数(Likelihood Function)可以表示为:
L ( θ ; X ) = P ( X ∣ θ ) = ∏ i = 1 n P ( x i ∣ θ ) L(\theta; X) = P(X|\theta) = \prod_{i=1}^n P(x_i|\theta) L(θ;X)=P(X∣θ)=i=1∏nP(xi∣θ)
为了简化计算,我们通常使用对数似然函数(Log-Likelihood Function):
ℓ ( θ ; X ) = log L ( θ ; X ) = ∑ i = 1 n log P ( x i ∣ θ ) \ell(\theta; X) = \log L(\theta; X) = \sum_{i=1}^n \log P(x_i|\theta) ℓ(θ;X)=logL(θ;X)=i=1∑nlogP(xi∣θ)
最大似然估计的目标是找到参数 θ \theta θ,使得对数似然函数 ℓ ( θ ; X ) \ell(\theta; X) ℓ(θ;X) 达到最大值。即:
θ ^ = arg max θ ℓ ( θ ; X ) \hat{\theta} = \arg \max_\theta \ell(\theta; X) θ^=argθmaxℓ(θ;X)
示例题目
正态分布的概率密度函数(PDF)可以表示为:
f ( x ∣ μ , σ 2 ) = 1 2 π σ 2 exp ( − ( x − μ ) 2 2 σ 2 ) f(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) f(x∣μ,σ2)=2πσ21exp(−2σ2(x−μ)2)
假设我们有一组观测数据 X = ( x 1 , x 2 , … , x n ) X = (x_1, x_2, \ldots, x_n) X=(x1,x2,…,xn),这些数据都来自于一个正态分布 N ( μ , σ 2 ) N(\mu, \sigma^2) N(μ,σ2)。我们希望估计正态分布的参数 μ \mu μ 和 σ 2 \sigma^2 σ2。
观测数据为 X = ( x 1 , x 2 , … , x n ) X = (x_1, x_2, \ldots, x_n) X=(x1,x2,…,xn)。
详细讲解
-
写出似然函数:根据正态分布的概率密度函数,似然函数可以写为:
似然函数 L ( μ , σ 2 ; X ) L(\mu, \sigma^2; X) L(μ,σ2;X) 是在给定参数 μ \mu μ 和 σ 2 \sigma^2 σ2 下,观测数据 X X X 出现的概率。对于独立同分布的数据,这个概率是每个数据点概率密度的乘积,即:
L ( μ , σ 2 ; X ) = ∏ i = 1 n f ( x i ∣ μ , σ 2 ) L(\mu, \sigma^2; X) = \prod_{i=1}^n f(x_i|\mu, \sigma^2) L(μ,σ2;X)=i=1∏nf(xi∣μ,σ2)将正态分布的概率密度函数代入似然函数中,得到:
L ( μ , σ 2 ; X ) = ∏ i = 1 n 1 2 π σ 2 exp ( − ( x i − μ ) 2 2 σ 2 ) L(\mu, \sigma^2; X) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x_i - \mu)^2}{2\sigma^2}\right) L(μ,σ2;X)=i=1∏n2πσ21exp(−2σ2(xi−μ)2)
对数似然函数
-
取对数:为了简化计算,取对数得到对数似然函数:
ℓ ( μ , σ 2 ; X ) = ∑ i = 1 n log ( 1 2 π σ 2 exp ( − ( x i − μ ) 2 2 σ 2 ) ) \ell(\mu, \sigma^2; X) = \sum_{i=1}^n \log \left( \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x_i - \mu)^2}{2\sigma^2}\right) \right) ℓ(μ,σ2;X)=i=1∑nlog(2πσ21exp(−2σ2(xi−μ)2))
进一步简化:
ℓ ( μ , σ 2 ; X ) = − n 2 log ( 2 π σ 2 ) − 1 2 σ 2 ∑ i = 1 n ( x i − μ ) 2 \ell(\mu, \sigma^2; X) = -\frac{n}{2} \log(2\pi\sigma^2) - \frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2 ℓ(μ,σ2;X)=−2nlog(2πσ2)−2σ21i=1∑n(xi−μ)2 -
求导并解方程:对 μ \mu μ 和 σ 2 \sigma^2 σ2 分别求导并令其等于零,可以得到参数的估计值。
对 μ \mu μ 求导:
∂ ℓ ∂ μ = 1 σ 2 ∑ i = 1 n ( x i − μ ) = 0 \frac{\partial \ell}{\partial \mu} = \frac{1}{\sigma^2} \sum_{i=1}^n (x_i - \mu) = 0 ∂μ∂ℓ=σ21i=1∑n(xi−μ)=0
解得:
μ ^ = 1 n ∑ i = 1 n x i \hat{\mu} = \frac{1}{n} \sum_{i=1}^n x_i μ^=n1i=1∑nxi对 σ 2 \sigma^2 σ2 求导:
∂ ℓ ∂ σ 2 = − n 2 σ 2 + 1 2 σ 4 ∑ i = 1 n ( x i − μ ) 2 = 0 \frac{\partial \ell}{\partial \sigma^2} = -\frac{n}{2\sigma^2} + \frac{1}{2\sigma^4} \sum_{i=1}^n (x_i - \mu)^2 = 0 ∂σ2∂ℓ=−2σ2n+2σ41i=1∑n(xi−μ)2=0
解得:
σ ^ 2 = 1 n ∑ i = 1 n ( x i − μ ) 2 \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \mu)^2 σ^2=n1i=1∑n(xi−μ)2
Python代码求解
import numpy as np# 观测数据
X = np.array([2.3, 1.9, 3.1, 2.8, 2.4])# 估计参数
mu_hat = np.mean(X)
sigma_squared_hat = np.var(X, ddof=0)print("估计的均值 μ:", mu_hat)
print("估计的方差 σ^2:", sigma_squared_hat)
实际生活中的例子
最大似然估计在实际生活中的应用广泛。例如,在医学研究中,科学家常常需要估计某种疾病的发病率。假设有一个新的传染病,研究人员需要估计其传播率(即,传染给某人的概率)。他们收集了若干病例数据,通过最大似然估计,可以得到传播率的最优估计,从而帮助制定防控策略。
最大似然估计同样可以应用于金融领域,比如估计股票的收益率和风险;在机器学习中,用于训练模型的参数,如线性回归中的回归系数等。
相关文章:

【数学】什么是最大似然估计?如何求解最大似然估计
背景 最大似然估计(Maximum Likelihood Estimation, MLE)是一种估计统计模型参数的方法。它在众多统计学领域中被广泛使用,比如回归分析、时间序列分析、机器学习和经济学。其核心思想是:给定一个观测数据集,找到一组…...

跟张良均老师学大数据人工智能|企业项目试岗实训开营
我国高校毕业生数量连年快速增长,从2021年的909万人到2022年的1076万人,再到2023年的1158万人,预计到2024年将达到1187万人,2024年高校毕业生数量再创新高。 当年高校毕业生人数不等于进入劳动力市场的高校毕业生人数&#x…...

Pentest Muse:一款专为网络安全人员设计的AI助手
关于Pentest Muse Pentest Muse是一款专为网络安全研究人员和渗透测试人员设计和开发的人工智能AI助手,该工具可以帮助渗透测试人员进行头脑风暴、编写Payload、分析代码或执行网络侦查任务。除此之外,Pentest Muse甚至还能够执行命令行代码并以迭代方式…...
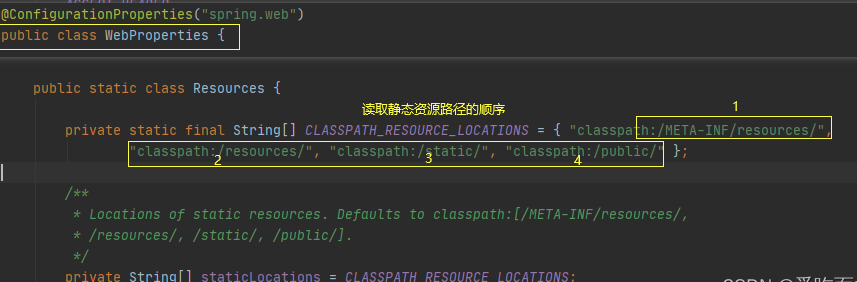
10 SpringBoot 静态资源访问
我们在开发Web项目的时候,往往会有很多静态资源,如html、图片、css等。那如何向前端返回静态资源呢? 以前做过web开发的同学应该知道,我们以前创建的web工程下面会有一个webapp的目录,我们只要把静态资源放在该目录下…...
Unity 之通过自定义协议从浏览器启动本地应用程序
内容将会持续更新,有错误的地方欢迎指正,谢谢! Unity 之通过自定义协议从浏览器启动本地应用程序 TechX 坚持将创新的科技带给世界! 拥有更好的学习体验 —— 不断努力,不断进步,不断探索 TechX —— 心探索、心进…...
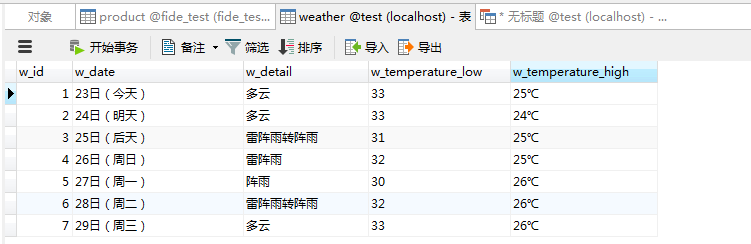
Python抓取天气信息
Python的详细学习还是需要些时间的。如果有其他语言经验的,可以暂时跟着我来写一个简单的例子。 2024年最新python教程全套,学完即可进大厂!(附全套视频 下载) (qq.com) 我们计划抓取的数据:杭州的天气信息…...
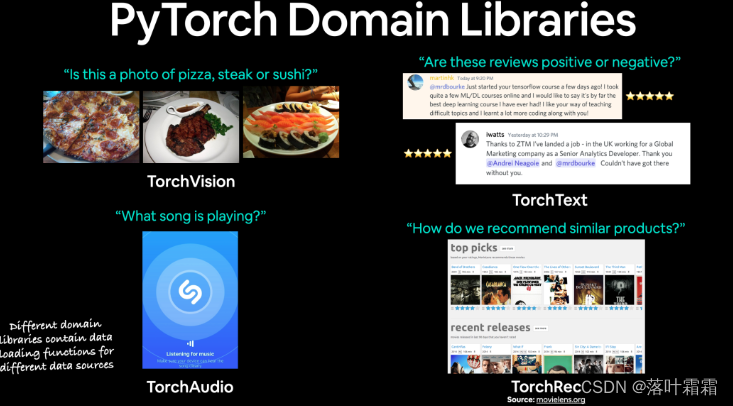
【超越拟合:深度学习中的过拟合与欠拟合应对策略】
如何处理过拟合 由于过拟合的主要问题是你的模型与训练数据拟合得太好,因此你需要使用技术来“控制它”。防止过拟合的常用技术称为正则化。我喜欢将其视为“使我们的模型更加规则”,例如能够拟合更多类型的数据。 让我们讨论一些防止过拟合的方法。 获…...

【Orange Pi 5与Linux内核编程】-理解Linux内核中的container_of宏
理解Linux内核中的container_of宏 文章目录 理解Linux内核中的container_of宏1、了解C语言中的struct内存表示2、Linux内核的container_of宏实现理解3、Linux内核的container_of使用 Linux 内核包含一个名为 container_of 的非常有用的宏。本文介绍了解 Linux 内核中的 contain…...

003.Linux SSH协议工具
我 的 个 人 主 页:👉👉 失心疯的个人主页 👈👈 入 门 教 程 推 荐 :👉👉 Python零基础入门教程合集 👈👈 虚 拟 环 境 搭 建 :👉&…...

web前端组织分析:深入剖析其结构、功能与未来趋势
web前端组织分析:深入剖析其结构、功能与未来趋势 在数字化浪潮的推动下,Web前端组织作为连接用户与数字世界的桥梁,其重要性日益凸显。本文将从四个方面、五个方面、六个方面和七个方面对Web前端组织进行深入分析,揭示其结构特点…...
GitCode热门开源项目推荐:Spider网络爬虫框架
在数字化高速发展时代,数据已成为企业决策和个人研究的重要资源。网络爬虫作为一种强大的数据采集工具受到了广泛的关注和应用。在GitCode这一优秀的开源平台上,Spider网络爬虫框架凭借其简洁、高效和易用性,成为了众多开发者的首选。 一、系…...

实现一个二叉树的前序遍历、中序遍历和后序遍历方法。
package test3;public class Test_A27 {// 前序遍历(根-左-右)public void preOrderTraversal(TreeNode root){if(rootnull){return;}System.out.println(root.val"");preOrderTraversal(root.left);preOrderTraversal(root.right);}// 中序遍…...
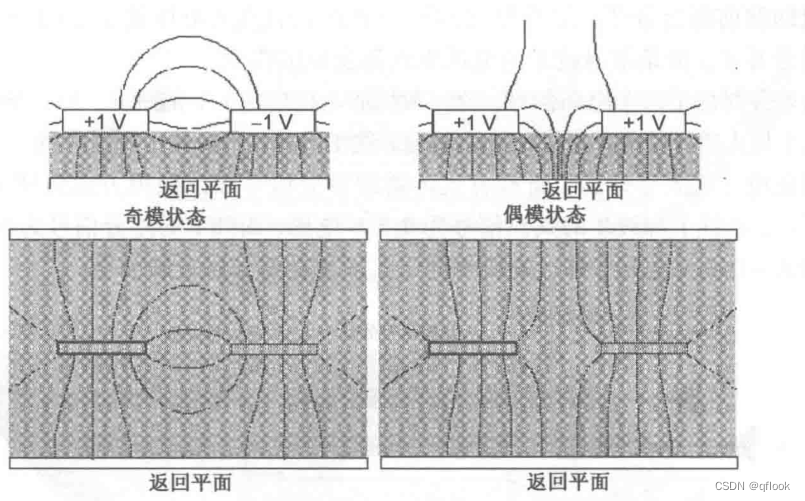
串扰(二)
三、感性串扰 首先看下串扰模型及电流方向: 由于电感是阻碍电流变化,受害线的电流方向和攻击线的电流方向相反。同时由于受害线阻抗均匀,故有Vb-Vf(感应电流属于电池内部电流)。 分析感性串扰大小仍然是按微分的方法…...
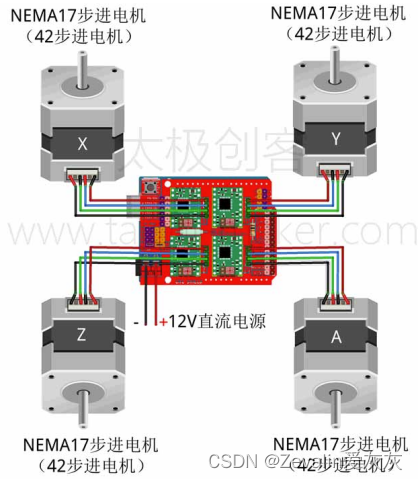
零基础入门学用Arduino 第四部分(三)
重要的内容写在前面: 该系列是以up主太极创客的零基础入门学用Arduino教程为基础制作的学习笔记。个人把这个教程学完之后,整体感觉是很好的,如果有条件的可以先学习一些相关课程,学起来会更加轻松,相关课程有数字电路…...

Mp3文件结构全解析(一)
Mp3文件结构全解析(一) MP3 文件是由帧(frame)构成的,帧是MP3 文件最小的组成单位。MP3的全称应为MPEG1 Layer-3 音频 文件,MPEG(Moving Picture Experts Group) 在汉语中译为活动图像专家组,特指活动影音压缩标准,MPEG 音频文件…...

ES 8.14 Java 代码调用,增加knnSearch 和 混合检索 mixSearch
1、pom依赖 <dependency><groupId>org.elasticsearch.client</groupId><artifactId>elasticsearch-rest-client</artifactId><version>8.14.0</version></dependency><dependency><groupId>co.elastic.clients<…...

被腰斩的颍川郡守赵广汉
在颍川,他发明了举报箱,铁腕扫黑除恶。因为曾经在郡府所在地阳翟(禹州)当过县令,熟悉颍川社情民意,所以,任职郡守后雷厉风行,才不到一年,不但制服了骄横的豪门大族&#…...
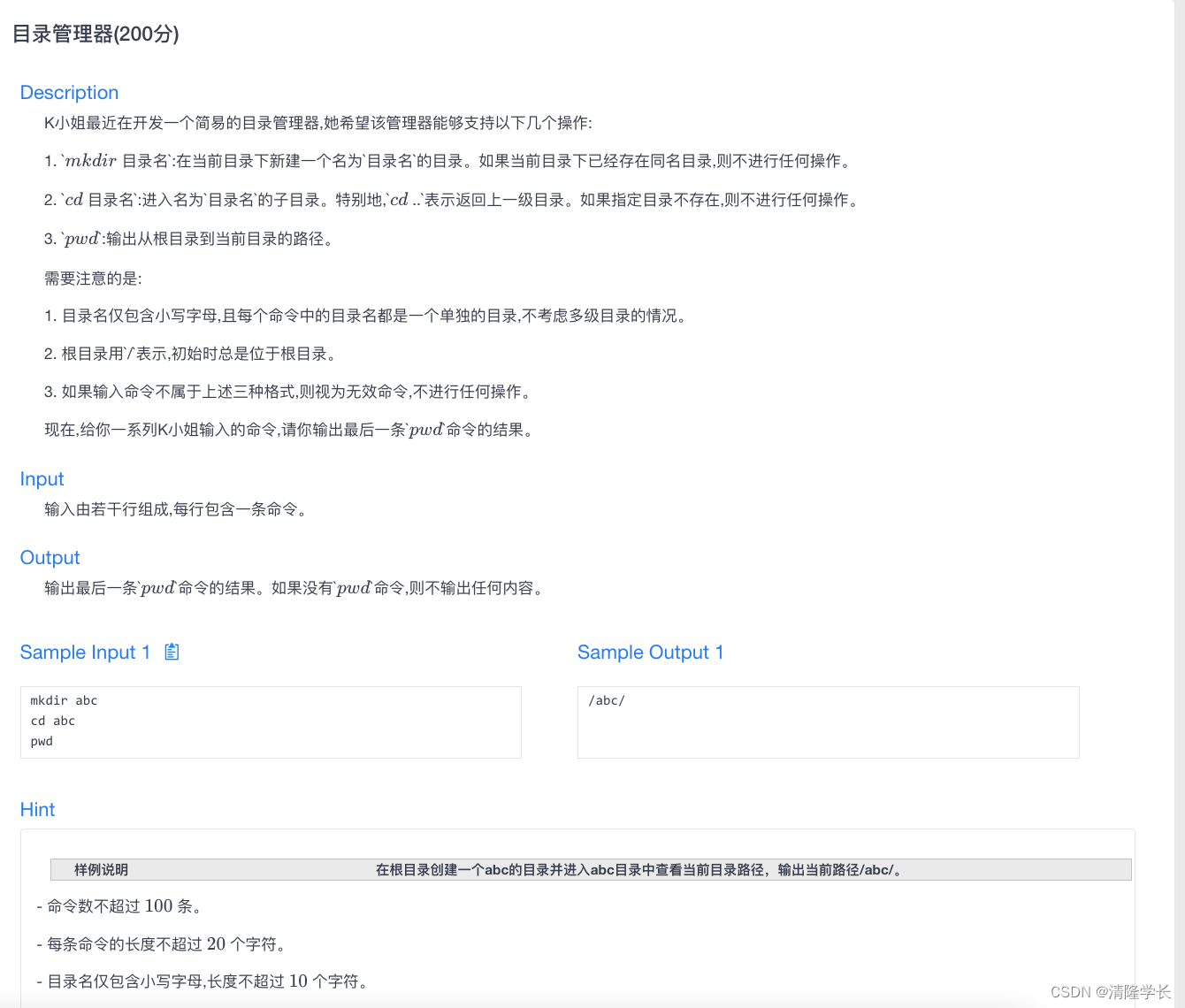
【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 目录管理器(200分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 📎在线评测链接 目录管理器(200分) 🌍 评测功能需要订阅专栏后私信联系清隆…...

关于自学\跳槽\转行做网络安全行业的一些建议
很好,如果你是被题目吸引过来的,那请看完再走,还是有的~ 为什么写这篇文章 如何自学入行?如何小白跳槽,年纪大了如何转行等类似问题 ,发现很多人都有这样的困惑。下面的文字其实是我以前的一个回答&#…...

计算机网络(1) OSI七层模型与TCP/IP四层模型
一.OSI七层模型 OSI 七层模型是国际标准化组织ISO提出的一个网络分层模型,它的目的是使各种不同的计算机和网络在世界范围内按照相同的标准框架实现互联。OSI 模型把网络通信的工作分为 7 层,从下到上分别是物理层、数据链路层、网络层、传输层、会话层、…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...

C++ 类基础:封装、继承、多态与多线程模板实现
前言 C 是一门强大的面向对象编程语言,而类(Class)作为其核心特性之一,是理解和使用 C 的关键。本文将深入探讨 C 类的基本特性,包括封装、继承和多态,同时讨论类中的权限控制,并展示如何使用类…...
