pytorch基础【4】梯度计算、链式法则、梯度清零
文章目录
- 梯度计算
- 计算图(Computational Graph)
- 梯度求导(Gradient Computation)
- 函数与概念
- 示例代码
- 更多细节
- 梯度求导的过程
- 梯度求导的基本步骤
- 示例代码
- 注意事项
- 总结
- 链式法则是什么?
- 链式法则的数学定义
- 链式法则在深度学习中的应用
- 反向传播中的链式法则
- 具体示例
- 反向传播过程
- 总结
- 为什么需要梯度清零
- 如何实现梯度清零
- 进一步说明
- 总结
梯度计算
在PyTorch中,计算图和梯度求导是核心功能之一,特别是在深度学习模型的训练过程中。以下是对这两个概念的详细解释:
计算图(Computational Graph)
计算图是一种有向无环图(Directed Acyclic Graph, DAG),其中节点表示操作(operation)或变量(variable),边表示操作的输入输出关系。PyTorch 使用计算图来记录和管理变量之间的依赖关系,以便在反向传播时计算梯度。
- 动态计算图(Dynamic Computational Graph):PyTorch 采用动态计算图(Dynamic Computational Graph),即每次进行前向传播(forward pass)时,都会动态构建一个新的计算图。这样做的好处是可以更灵活地处理各种复杂的模型结构,尤其是那些在每个前向传播中都会变化的模型。
梯度求导(Gradient Computation)
梯度求导是深度学习中优化模型参数的关键步骤。梯度描述了损失函数对每个参数的变化率,用于指导参数的更新方向。
- 自动求导(Autograd):PyTorch 提供了一个强大的自动求导库,称为 Autograd。通过 Autograd,PyTorch 可以自动计算标量值(通常是损失函数)的梯度。
函数与概念
torch.Tensor:Tensor是 PyTorch 中存储数据和定义计算图的基础数据结构。默认情况下,所有的张量(Tensor)都不会自动追踪计算的历史。- 如果要使张量参与计算图并能够进行自动求导,需要在创建张量时设置
requires_grad=True。
backward():- 调用张量的
backward()方法,PyTorch 会自动计算该张量的所有依赖张量的梯度,并存储在各自的.grad属性中。 backward()只接受标量张量(一个数值),如果不是标量张量,通常会传递一个与张量形状匹配的梯度参数。
- 调用张量的
torch.no_grad():- 在评估模型或推理时,我们不需要计算梯度,可以使用
torch.no_grad()以节省内存和计算资源。
- 在评估模型或推理时,我们不需要计算梯度,可以使用
示例代码
import torch# 创建张量,并设置 requires_grad=True 以追踪其计算历史
x = torch.tensor(2.0, requires_grad=True)
y = x ** 2# 计算图中 y 的梯度
y.backward() # 计算 y 对 x 的梯度
print(x.grad) # 输出 x 的梯度,dy/dx = 2*x => 4# 在不需要梯度计算的情况下进行计算
with torch.no_grad():z = x * 2print(z) # 输出:tensor(4.0)
更多细节
- 梯度累积与清零:每次调用
backward(),梯度会累积(即,累加到.grad属性中),因此在每次新的梯度计算之前通常需要清零现有的梯度,例如通过optimizer.zero_grad()。 - 多次反向传播:如果在同一个计算图上进行多次反向传播(例如在 RNN 中),需要设置
retain_graph=True,以防止计算图被释放。
通过这些机制,PyTorch 提供了一个灵活且高效的框架,用于构建和训练复杂的神经网络模型。
梯度求导的过程
在PyTorch中,梯度求导的过程是通过自动微分(Autograd)机制实现的。以下是梯度求导过程的详细步骤:
梯度求导的基本步骤
- 定义计算图:
- 每当你对
torch.Tensor进行操作时,PyTorch 会动态地创建一个计算图来记录操作。 - 如果
Tensor的requires_grad属性设置为True,那么该张量会开始追踪其上的所有操作,这样你就可以调用backward()来自动计算其梯度。
- 每当你对
- 前向传播(Forward Pass):
- 计算图的构建是在前向传播过程中完成的。在前向传播过程中,输入数据通过神经网络的各层进行计算,最终生成输出。
- 计算损失(Loss Calculation):
- 通常情况下,在前向传播结束后会计算损失函数(Loss),这是一个标量值,用于评估模型的输出与目标之间的差距。
- 反向传播(Backward Pass):
- 调用损失张量的
backward()方法。反向传播通过链式法则计算损失函数相对于每个叶子节点(即,所有具有requires_grad=True的张量)的梯度。
- 调用损失张量的
- 更新参数(Parameter Update):
- 使用优化器(如 SGD、Adam 等)通过梯度下降或其他优化算法更新模型的参数。
示例代码
以下是一个简单的示例代码,演示了梯度求导的过程:
import torch
import torch.nn as nn
import torch.optim as optim# 定义一个简单的线性模型
class LinearModel(nn.Module):def __init__(self):super(LinearModel, self).__init__()self.linear = nn.Linear(1, 1) # 输入维度为1,输出维度为1def forward(self, x):return self.linear(x)# 创建模型实例
model = LinearModel()# 定义损失函数和优化器
criterion = nn.MSELoss() # 均方误差损失函数
optimizer = optim.SGD(model.parameters(), lr=0.01) # 随机梯度下降优化器# 创建输入数据和目标数据
inputs = torch.tensor([[1.0], [2.0], [3.0], [4.0]])
targets = torch.tensor([[2.0], [4.0], [6.0], [8.0]])# 前向传播
outputs = model(inputs)
loss = criterion(outputs, targets)# 反向传播
loss.backward()# 查看梯度
for param in model.parameters():print(param.grad)# 更新参数
optimizer.step()
步骤解析
- 创建模型和数据:
- 定义一个简单的线性回归模型,并创建输入数据和目标数据。
- 前向传播:
- 将输入数据传递给模型,计算输出。
- 使用损失函数计算输出与目标之间的损失。
- 反向传播:
- 调用
loss.backward()计算损失相对于每个参数的梯度。PyTorch 会通过计算图自动进行反向传播,计算各个参数的梯度并存储在param.grad中。
- 调用
- 更新参数:
- 使用优化器的
step()方法更新参数。这一步通常在每个训练迭代中执行。
- 使用优化器的
注意事项
- 梯度清零:在每次调用
backward()之前,通常需要清零现有的梯度,以避免梯度累积。这可以通过optimizer.zero_grad()或model.zero_grad()来实现。 - 链式法则:反向传播过程中使用链式法则计算梯度,因此在计算图较深时,梯度的计算会逐层进行,直到计算到每个叶子节点。
总结
PyTorch 的自动微分机制使得梯度计算变得简单且高效,通过构建计算图并自动进行反向传播,你可以专注于模型的设计和训练,而不必手动计算复杂的梯度。
链式法则是什么?
链式法则(Chain Rule)是微积分中的一个基本法则,用于求复合函数的导数。在深度学习中,链式法则用于反向传播(backpropagation)算法的核心,帮助计算损失函数相对于每个模型参数的梯度。
链式法则的数学定义
假设有两个函数 u=f(x) 和 y=g(u),那么复合函数 y=g(f(x)) 的导数可以表示为:
d y d x = d y d u ⋅ d u d x \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} dxdy=dudy⋅dxdu
链式法则在深度学习中的应用
在深度学习中,神经网络由多个层组成,每一层可以看作是一个函数,这些函数依次连接形成一个复合函数。假设我们有一个三层的神经网络,其前向传播可以表示为:
- a=f(x)
- b=g(a)
- c=h(b)
损失函数 L可以表示为 L=l©,其中 x 是输入数据,a、b、c 是中间层的输出。
反向传播中的链式法则
在反向传播过程中,我们需要计算损失函数 L对每个参数的梯度。通过链式法则,我们可以逐层计算这些梯度。具体步骤如下:
-
计算损失函数相对于输出层的梯度:
∂ L ∂ c \frac{\partial L}{\partial c} ∂c∂L -
计算损失函数相对于中间层 b的梯度:
∂ L ∂ b = ∂ L ∂ c ⋅ ∂ c ∂ b \frac{\partial L}{\partial b} = \frac{\partial L}{\partial c} \cdot \frac{\partial c}{\partial b} ∂b∂L=∂c∂L⋅∂b∂c -
计算损失函数相对于中间层 a 的梯度:
∂ L ∂ a = ∂ L ∂ b ⋅ ∂ b ∂ a \frac{\partial L}{\partial a} = \frac{\partial L}{\partial b} \cdot \frac{\partial b}{\partial a} ∂a∂L=∂b∂L⋅∂a∂b -
计算损失函数相对于输入层 x的梯度:
∂ L ∂ x = ∂ L ∂ a ⋅ ∂ a ∂ x \frac{\partial L}{\partial x} = \frac{\partial L}{\partial a} \cdot \frac{\partial a}{\partial x} ∂x∂L=∂a∂L⋅∂x∂a
通过这种逐层传播梯度的方式,我们可以计算每个参数的梯度,从而使用梯度下降法来更新模型参数。
具体示例
让我们通过一个具体的例子来说明链式法则的应用。假设我们有一个简单的神经网络,其前向传播过程如下:
-
输入 xxx
-
第一层:
z 1 = W 1 x + b 1 z_1=W_1x+b_1 z1=W1x+b1,激活函数
a 1 = σ ( z 1 ) a_1 = \sigma(z_1) a1=σ(z1) -
第二层:
z 2 = W 2 a 1 + b 2 z_2 = W_2 a_1 + b_2 z2=W2a1+b2
,激活函数
a 2 = σ ( z 2 ) a_2 = \sigma(z_2) a2=σ(z2) -
输出层:
y = W 3 a 2 + b 3 y = W_3 a_2 + b_3 y=W3a2+b3
损失函数 L 是输出 y 和目标 ytarget之间的均方误差。
反向传播过程
计算输出层的梯度:
∂ L ∂ y = 2 ( y − y t a r g e t ) \frac{\partial L}{\partial y} = 2 (y - y_{target}) ∂y∂L=2(y−ytarget)
计算第二层的梯度:
∂ L ∂ z 2 = ∂ L ∂ y ⋅ ∂ y ∂ z 2 = ∂ L ∂ y ⋅ W 3 \frac{\partial L}{\partial z_2} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial z_2} = \frac{\partial L}{\partial y} \cdot W_3 ∂z2∂L=∂y∂L⋅∂z2∂y=∂y∂L⋅W3
∂ L ∂ a 2 = ∂ L ∂ z 2 ⋅ σ ′ ( z 2 ) ∂ \frac{\partial L}{\partial a_2} = \frac{\partial L}{\partial z_2} \cdot \sigma'(z_2)∂ ∂a2∂L=∂z2∂L⋅σ′(z2)∂
计算第一层的梯度:
∂ L ∂ z 1 = ∂ L ∂ a 2 ⋅ ∂ a 2 ∂ z 1 = ∂ L ∂ a 2 ⋅ W 2 \frac{\partial L}{\partial z_1} = \frac{\partial L}{\partial a_2} \cdot \frac{\partial a_2}{\partial z_1} = \frac{\partial L}{\partial a_2} \cdot W_2 ∂z1∂L=∂a2∂L⋅∂z1∂a2=∂a2∂L⋅W2
∂ L ∂ a 1 = ∂ L ∂ z 1 ⋅ σ ′ ( z 1 ) \frac{\partial L}{\partial a_1} = \frac{\partial L}{\partial z_1} \cdot \sigma'(z_1) ∂a1∂L=∂z1∂L⋅σ′(z1)
计算输入层的梯度:
∂ L ∂ x = ∂ L ∂ a 1 ⋅ W 1 \frac{\partial L}{\partial x} = \frac{\partial L}{\partial a_1} \cdot W_1 ∂x∂L=∂a1∂L⋅W1
通过链式法则,反向传播算法能够有效地计算出每一层参数的梯度,从而更新参数,最小化损失函数。
总结
链式法则是微积分中的一个重要法则,它在深度学习中的反向传播算法中起到了关键作用。通过链式法则,我们可以有效地计算复合函数的导数,从而利用梯度下降等优化方法来训练神经网络模型。
在深度学习中,梯度清零(zeroing gradients)是训练过程中的一个关键步骤,通常在每次参数更新之前进行。这个过程在PyTorch等深度学习框架中尤为重要。以下是关于为什么需要梯度清零以及如何实现梯度清零的详细解释:
为什么需要梯度清零
- 防止梯度累积:
- 在每次反向传播计算中,梯度会累积到模型参数的
.grad属性中。如果不清零,梯度会在每个小批次(mini-batch)训练后继续累积,这将导致错误的梯度更新。 - 举例来说,如果没有清零,当前批次的梯度会与之前批次的梯度相加,导致最终的梯度远大于实际应该的值。这会使参数更新的步长不合理,影响模型训练效果。
- 在每次反向传播计算中,梯度会累积到模型参数的
- 正确的参数更新:
- 每个小批次的梯度计算都应该基于当前的小批次数据,确保每次参数更新都准确反映当前的小批次数据对损失函数的贡献。
如何实现梯度清零
在PyTorch中,梯度清零通常通过调用 optimizer.zero_grad() 来实现。这里有一个完整的例子来说明这一过程:
import torch
import torch.nn as nn
import torch.optim as optim# 定义一个简单的神经网络
class SimpleNet(nn.Module):def __init__(self):super(SimpleNet, self).__init__()self.fc1 = nn.Linear(10, 5)self.fc2 = nn.Linear(5, 1)def forward(self, x):x = torch.relu(self.fc1(x))x = self.fc2(x)return x# 实例化模型和优化器
model = SimpleNet()
optimizer = optim.SGD(model.parameters(), lr=0.01)# 生成一些假数据
data = torch.randn(10) # 输入数据
target = torch.tensor([1.0]) # 目标标签# 损失函数
criterion = nn.MSELoss()# 训练过程中的一个小批次
for epoch in range(100): # 假设训练100个epochoptimizer.zero_grad() # 清零梯度output = model(data) # 前向传播loss = criterion(output, target) # 计算损失loss.backward() # 反向传播计算梯度optimizer.step() # 更新参数
进一步说明
- 清零位置:
optimizer.zero_grad()通常放在每个训练循环的开头,确保在计算新的梯度之前先将上一次迭代的梯度清零。 - 梯度累积应用场景: 在某些特定情况下,例如梯度累积(Gradient Accumulation)技术中,故意让梯度在多个小批次上累积,然后再更新参数。但这是特定应用场景,不适用于标准的训练过程。
总结
梯度清零是深度学习模型训练中的一个重要步骤,确保每次参数更新时的梯度计算是正确的、独立的。通过 optimizer.zero_grad() 方法,我们可以有效地防止梯度累积问题,从而确保模型训练过程的稳定性和准确性。
相关文章:

pytorch基础【4】梯度计算、链式法则、梯度清零
文章目录 梯度计算计算图(Computational Graph)梯度求导(Gradient Computation)函数与概念 示例代码更多细节梯度求导的过程梯度求导的基本步骤示例代码注意事项总结 链式法则是什么?链式法则的数学定义链式法则在深度…...

mapreduce综合应用案例 — 招聘数据清洗
MapReduce是一个编程模型和处理大数据集的框架,它由Google开发并广泛使用于分布式计算环境中。MapReduce模型包含两个主要的函数:Map和Reduce。Map函数用于处理输入的键值对生成中间键值对,Reduce函数则用于合并Map函数输出的具有相同键的中间…...

发力采销,京东的“用户关系学”
作者 | 曾响铃 文 | 响铃说 40多岁打扮精致的城市女性,在西藏那曲的偏远农村,坐着藏民的摩托车,行驶在悬崖边的烂泥路上,只因为受顾客的“委托”,要寻找最原生态的藏区某款产品。 30多岁的憨厚中年男性,…...

期望23K,go高级社招面试复盘
面经哥只做互联网社招面试经历分享,关注我,每日推送精选面经,面试前,先找面经哥 我最终还是上岸了,花了一周总结了3万字的go社招高级面试知识体系思维导图,分享出来希望能帮助有缘人吧,以下只是…...
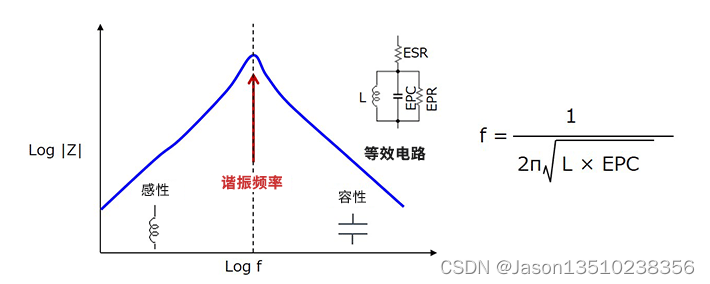
电感(线圈)具有哪些基本特性
首先,电感(线圈)具有以下基本特性,称之为“电感的感性电抗” ?①直流基本上直接流过。 ?②对于交流,起到类似电阻的作用。 ?③频率越高越难通过。 下面是表示电感的频率和阻抗特性的示意图。 在理想电感器中&#…...
tkinter实现一个GUI界面-快速入手
目录 一个简单界面输出效果其他功能插入进度条文本框内容输入和删除标签内容显示和删除 一个简单界面 含插入文本、文本框、按钮、按钮调用函数 # -*- coding: UTF-8 -*-import tkinter as tk from tkinter import END from tkinter import filedialog from tkinter impor…...
Top10在线音频剪辑软件,你了解几款?(免费分享)
多年来,随着音乐制作人和音频工程师的需求不断增长,音频剪辑软件领域经历了巨大的发展。最新的音频剪辑软件提供了从基本录制到最终发布所需的一切功能。其中一些软件专为播客设计,一些软件是免费的,并且一些软件提供了出色的音效…...

mysql报错:You can‘t specify target table ‘Person‘ for update in FROM clause
背景 在做leetcode里数据库的196题删除重复数据时,我参考评论区大佬的方法先用group by找到每个分组里的最小的id的那条记录,然后删掉原表中id不在其中的记录,然后就报了如题所示的错误。 我的写法如下: DELETE FROMPerson WHER…...
方法)
Python sorted()方法
sorted() 是Python中的一个内置函数,用于对可迭代对象进行排序。它返回一个新的已排序的列表,而不会修改原始的可迭代对象。sorted() 函数的基本语法如下: sorted(iterable, keyNone, reverseFalse)参数解释: iterableÿ…...
云上宝库:三大厂商对象存储安全性及差异性比较
前言 看了几家云厂商的对象存储,使用上有相似也有差异,聊聊阿里云、腾讯云、京东云三家对象存储在使用中存在的风险以及防护措施。 0x01 云存储命名 阿里云对象存储OSS(Object Storage Service),新用户免费试用三个月,存储包容…...
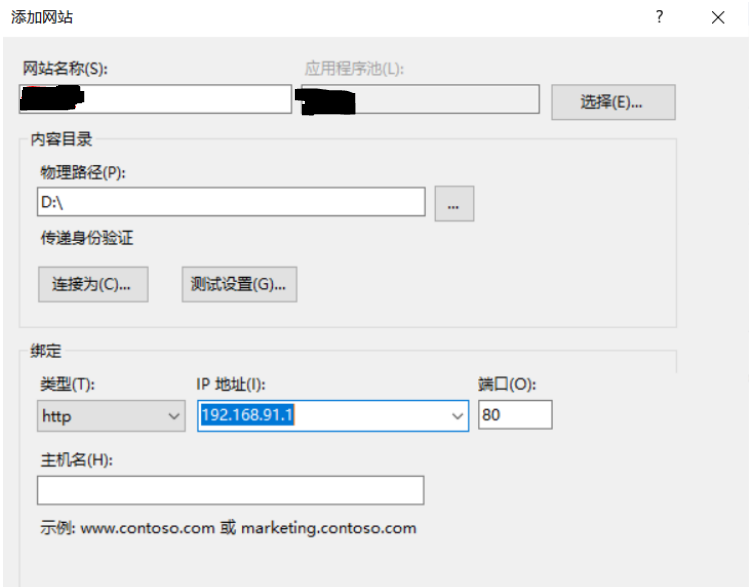
【计算机网络体系结构】计算机网络体系结构实验-www实验
二、www实验 1. 添加网站 2. 浏览器打开...

Windows下MySQL数据库定期备份SQL文件与删除历史备份文件.bat脚本
目录 一、功能需求 二、解决方案 (1)新建文件夹及批处理文件 (2)编写备份脚本 ①完整脚本 ②参数修改 (3)编写定期删除备份脚本 ①根据文件名识别日期进行删除 ② 根据文件的修改日期删除 (4)设置定时器 (5)常见报错与处理 一、功能需求 在Windows系统下…...
electron基础使用
安装以及运行 当前node版本18,按照官网提供操作,npm init进行初始化操作,将index.js修改为main.js,执行npm install --save-dev electron。(这里我挂梯子下载成功了。),添加如下代码至package.…...
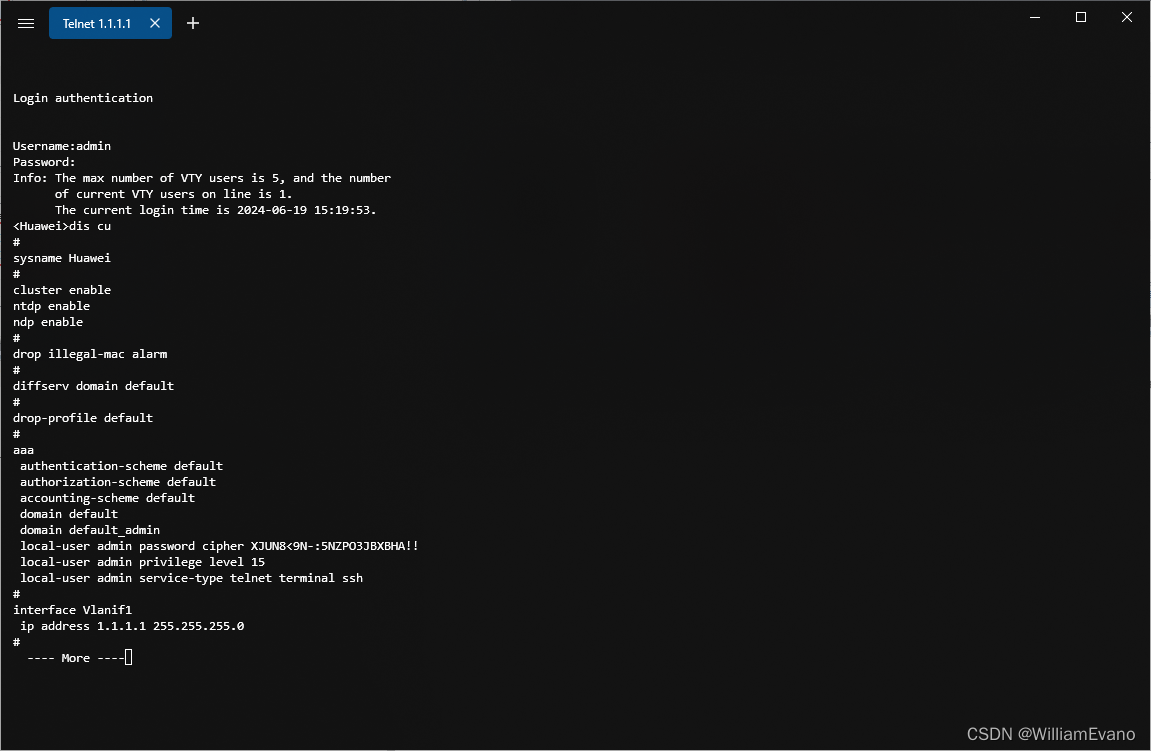
9.华为交换机telnet远程管理配置aaa认证
目的:telnet远程管理设备 LSW1配置 [Huawei]int Vlanif 1 [Huawei-Vlanif1]ip add 1.1.1.1 24 [Huawei-Vlanif1]q [Huawei]user-interface vty 0 4 [Huawei-ui-vty0-4]authentication-mode aaa [Huawei-ui-vty0-4]q [Huawei]aaa [Huawei-aaa]local-user admin pass…...
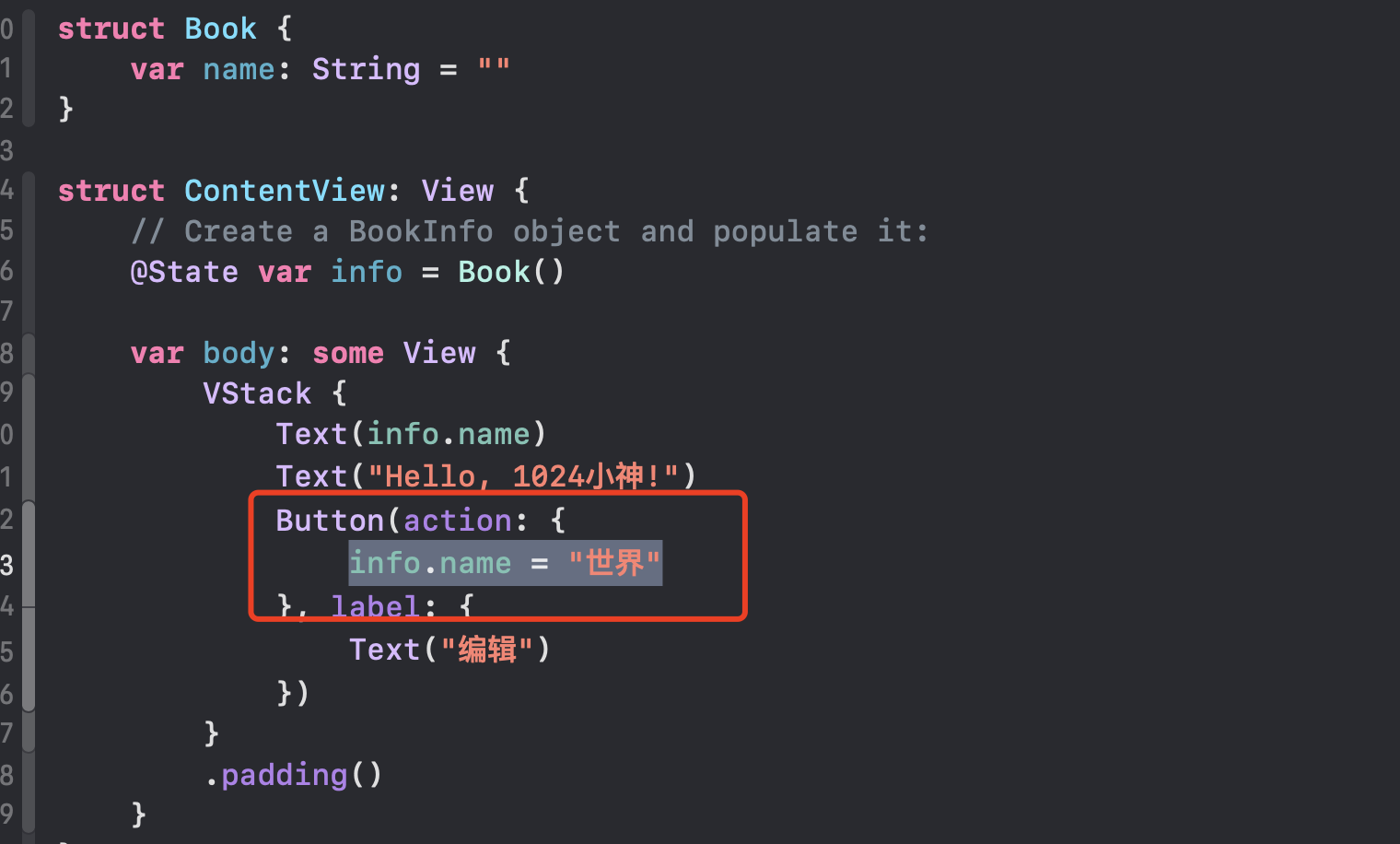
xcode报错合集,你都遇到过哪些跳不过的坑
1.报错Consecutive declarations on a line must be separated by ; 其实我这里是用因为创建了一个结构体,然后在没有使用State的情况下,修改它的属性了 当然加上State依然报错: 应该在UI事件中修改:...

六面体大米装袋机长期稳定运行原因分析
随着现代化农业生产的发展,六面体大米装袋机已成为粮食加工行业不可或缺的重要设备。然而,如何确保这些机器长期稳定运行,提高生产效率,降低维护成本,一直是广大粮食加工企业关注的焦点。星派将为您揭示六面体大米装袋…...

android的surface
相信很多Android开发者都知道Canvas类是UI的画布(虽然这种说法并不严谨),因为我们在Canvas上完成各种图形的绘制,那么我们Activity上的各种交互控件又是如何展示并渲染到屏幕上的呢,所以在另一个层面上也有一个“画布”…...

Z世代职场价值观的重塑:从“班味”心态到个人成长的追求
近日,社交平台Soul APP联合上海市精神卫生中心(俗称“宛平南路600号”)发布《2024年Z世代职场心理健康报告》(下称“报告”),发现今天的年轻人正以其独特的价值观和行为模式,重新定义成功与成就…...

【Python】Python 2 测试网络连通性脚本
文章目录 前言1. 命令行传参2. 代码 前言 最近在只有python2的服务器上部署服务,不能用三方类库,这里出于好奇心学习下python。这里简单做个脚本,实现了检验网络连通性的功能(类似于curl)。 1. 命令行传参 使用命令…...
瓦罗兰特教你怎么玩低价区+超适配低价区的免费加速器
《无畏契约》(VALORANT)是一款款英雄为核心的5V5第一人称战术射击PC游戏。在瓦罗兰特游戏中,玩家完成每日任务即可以获得大量的经验升级,另外我们也可以多多完成主线和支线任务,来加快升级的速度。玩家通过挑战副本&am…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
