Java数据结构与算法(完全背包)
前言:
完全背包问题是背包问题的一个变种,与0/1背包问题不同,在完全背包问题中,每种物品可以被选取多次。问题描述如下:
给定 n 件物品,每件物品有一个重量 wi和一个价值 vi,以及一个背包,它能够承载的最大重量为 W。我们需要确定应该将哪些物品放入背包,以使得背包内物品的总价值最大。
背包问题分类:
- 0-1背包问题 Java数据结构与算法(0/1背包问题)-CSDN博客
- 完全背包问题
- 多重背包问题
- 混合背包问题
- 二维背包问题
- 分组背包问题
- 有依赖的背包问题 (困难)
解题思路:
动态规划是解决完全背包问题的常用方法。我们可以通过修改0/1背包问题的动态规划方法来实现。
核心思想: 构建一个一维数组 dp[j],其中 j 表示当前背包容量。dp[j] 表示容量为 j 的背包中可以获得的最大价值。
状态转移方程:
- 如果选择第 i件物品:
dp[j] = max(dp[j], dp[j - wi] + vi)
实现代码
public class CompleteKnapsack {public static int completeKnapsack(int W, int[] weights, int[] values, int n) {int[] dp = new int[W + 1];for (int i = 0; i < n; i++) {for (int j = weights[i]; j <= W; j++) {dp[j] = Math.max(dp[j], dp[j - weights[i]] + values[i]);}}return dp[W];}public static void main(String[] args) {int W = 50; // 背包容量int[] weights = {10, 20, 30}; // 物品重量int[] values = {60, 100, 120}; // 物品价值int n = values.length;System.out.println("最大价值: " + completeKnapsack(W, weights, values, n));}
}
QA1:0/1背包和完全背包dp设计的差异作用?
dp[i]的作用就是用于区分一个物品能否重复放置,具体获取的值可以输出打印细细体会。
相关文章:
)
Java数据结构与算法(完全背包)
前言: 完全背包问题是背包问题的一个变种,与0/1背包问题不同,在完全背包问题中,每种物品可以被选取多次。问题描述如下: 给定 n 件物品,每件物品有一个重量 wi和一个价值 vi,以及一个背包,它能…...
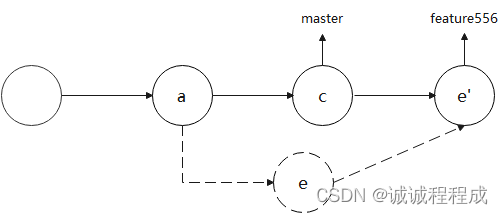
git merge(3个模式) 与 git rebase 图文详解区别
目录 1 git merge1.1 模式一:fast-forward(–ff)1.2 模式二:non-Fast-forward(–no-ff)1.3 模式三:fast-forward only(–ff-only) 2 git rebase3 区别 1 git merge git merge有好几种不同的模式 默认情况下你直接使用 git merge 命令&#x…...

Eclipse 工作空间:深入解析与高效使用
Eclipse 工作空间:深入解析与高效使用 Eclipse 是一款广受欢迎的集成开发环境(IDE),它为各种编程语言提供了强大的开发工具。在 Eclipse 中,工作空间(Workspace)是一个核心概念,它代表了一个项目的集合,这些项目共享相同的配置和设置。本文将深入探讨 Eclipse 工作空…...
Aspose将doc,ppt转成pdf
1.需要引入的jar包 链接: https://pan.baidu.com/s/1t3wqq7KrHi50K9KX3-Eb9A?pwdu4se 提取码: u4se <dependency><groupId>com.aspose</groupId><artifactId>aspose-words-jdk16</artifactId><version>15.8.0</version><scop…...
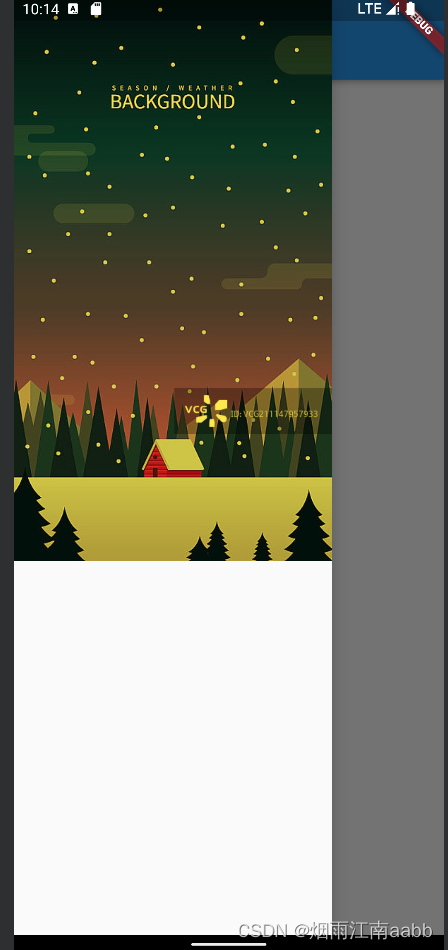
Flutter第十四弹 抽屉菜单效果
目标: 1.怎么构建抽屉菜单效果? 2.抽屉菜单怎么定制? 一、抽屉菜单 侧滑抽屉菜单效果 1.1 抽屉菜单入口 Flutter 的脚手架Scaffold,默认提供了抽屉菜单效果入口。 主页面采用一个简单的页面,侧滑菜单首先使用一个I…...
Docker Nginx
Docker官网 https://www.docker.com/https://www.docker.com/ 删除原先安装的Docker sudo yum remove docker \ docker-client \ docker-client-latest \ docker-common \ docker-latest \ …...

OpenVINO™ 2024.2 发布--推出LLM专属API !服务持续增强,提升AI生成新境界
点击蓝字 关注我们,让开发变得更有趣 作者 | 武卓 博士 排版 | 李擎 Hello, OpenVINO™ 2024.2 对我们来说,这是非常忙碌的几周,因为我们正在努力根据您的反馈改进我们的产品特性,并扩展生态系统以涵盖其它场景和用例。 让我们看看…...
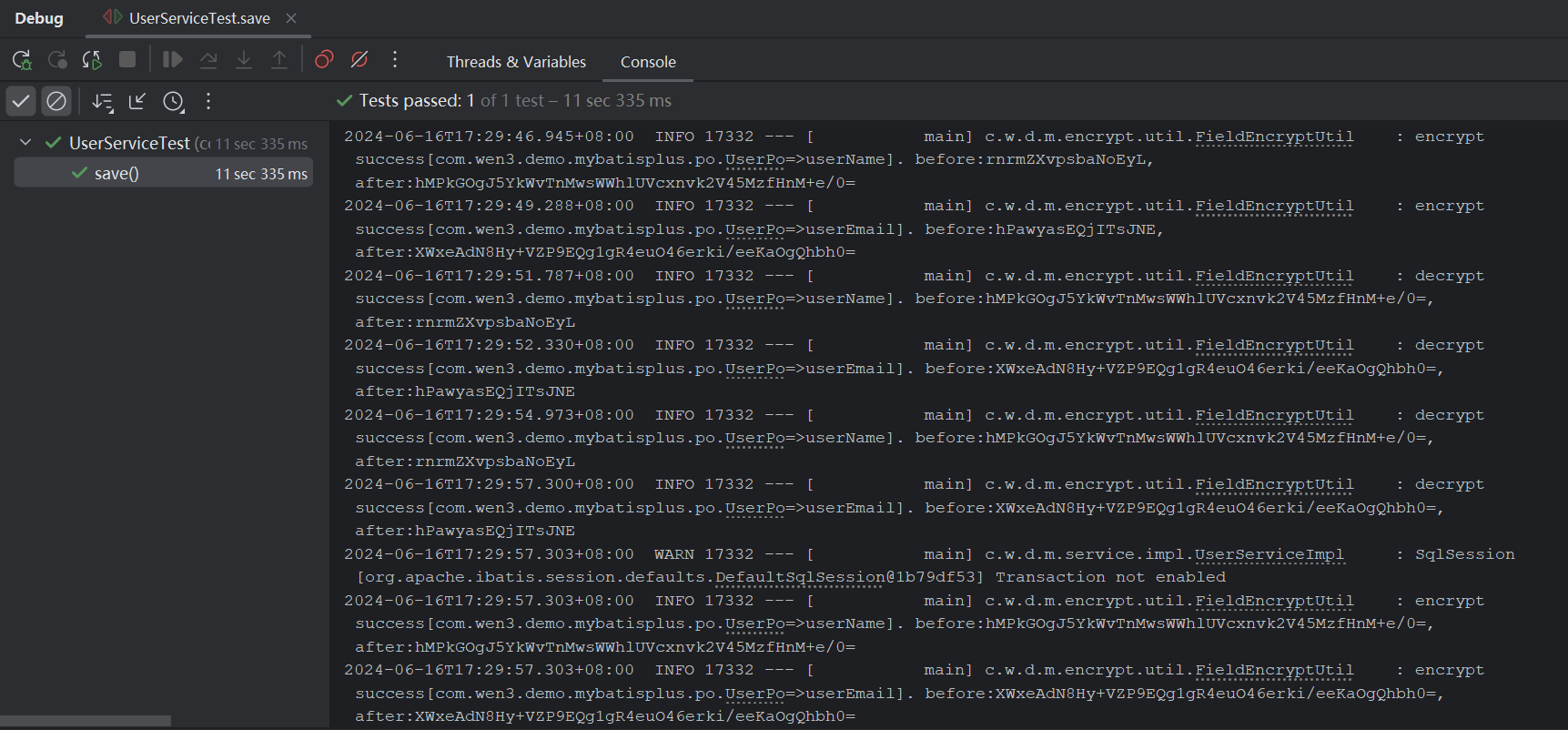
【Mybatis-Plus】根据自定义注解实现自动加解密
背景 我们把数据存到数据库的时候,有些敏感字段是需要加密的,从数据库查出来再进行解密。如果存在多张表或者多个地方需要对部分字段进行加解密操作,每个地方都手写一次加解密的动作,显然不是最好的选择。如果我们使用的是Mybati…...

Window上ubuntu子系统编译Android
Window上ubuntu子系统编译Android 1、编译环境2、WSL2编译报错2.1 You are building on a machine with 11.6GB of RAM2.2 Case-insensitive filesystems not supported3. android模拟器调试 1、编译环境 AOSP : Android源码下载安装java:sudo apt-get install ope…...
【Java学习笔记】异常处理
生活中我们在使用一些产品的时候,经常会碰到一些异常情况。例如,使用ATM机取钱的时,机器会突然出现故障导致无法完成正常的取钱业务,甚至吞卡;在乘坐地铁时,地铁出现异常无法按时启动和运行;使用…...

Ubuntu20.04环境下Baxter机器人开发环境搭建
Ubuntu20.04环境下Baxter机器人开发环境搭建 ubuntu20.04安装 略 安装ROS 略 Baxter机器人依赖安装 主目录创建工作空间,按以下步骤执行 mkdir -p ~/baxter_ws/src source /opt/ros/noetic/setup.bash cd ~/baxter_ws catkin_make catkin_make install s…...
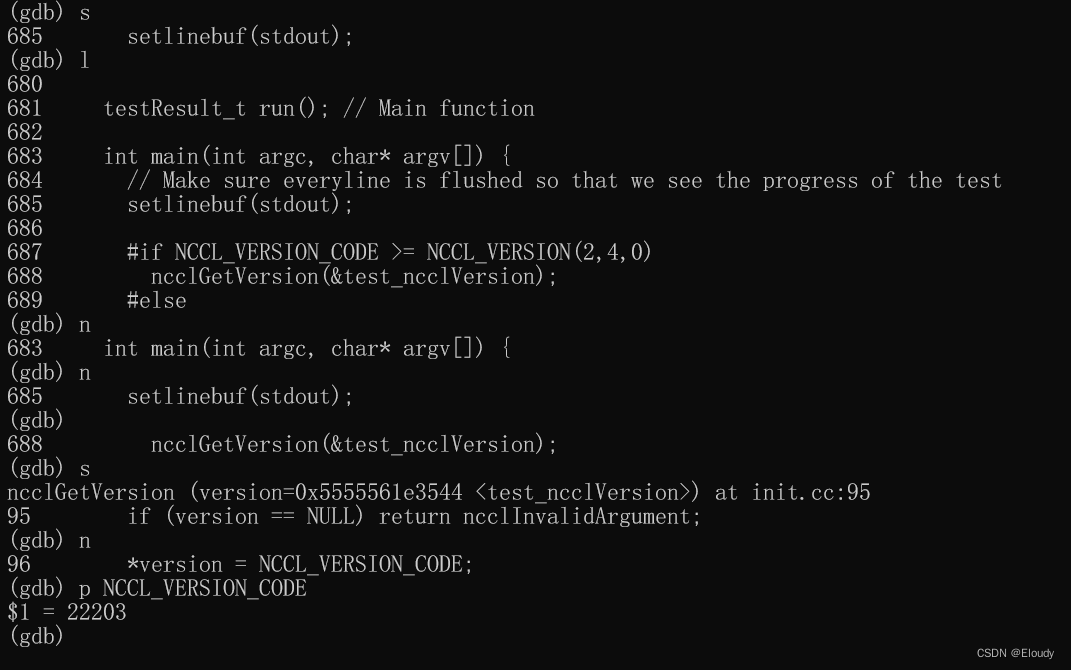
nccl 03 记 回顾:从下载,编译到调试 nccl-test
1, 下载与编译 1.1 源码下载 $ git clone https://github.com/NVIDIA/nccl.git 1.2 编译 1.2.1 一般编译: $ make -j src.build 1.2.2 特定架构gpu 编译 $ make -j src.build NVCC_GENCODE"-gencodearchcompute_80,codesm_80" A10…...

关于车规级功率器件热可靠性测试的分享
随着中国电动汽车市场的稳步快速发展和各大车企布局新能源的扩散,推动了车规级功率器件的快速增长。新能源汽车行业和消费电子都会用到半导体芯片,但车规级芯片对外部环境要求很高,涉及到的一致性和可靠性均要大于工业级产品要求,…...

内核学习——1、list_head
双向循环链表:list_head 头节点head是不使用的: struct list_head { struct list_head *next, *prev; }; 结构体中没有数据域,所以一般把list_head嵌入到其他结构中使用 struct file_node { char c; struct list_head node; }; 此时ÿ…...

JavaEE初阶--网络基本概念
目录 一、引言 二、网络基本概念 2.1 局域网LAN 2.2 广域网WAN 三、网络通信的基础 3.1 IP地址 3.2 端口号 3.3 协议 3.4 五元组 3.5 协议分层 3.6 OSI七层模型 3.7 TCP/IP五层模型 四、总结 一、引言 本篇博客将进入网络编程以及网络原理的学习,但网…...
gitlab-cicd-k8s
k8s已经准备好 kubectl get node 创建cicdYaml文件 kubectl create namespace gitlab-cicd --dry-runclient --outputyaml >> gitlab-cicd.yaml kubectl apply -f gitlab-cicd.yaml 服务器和仓库在一起可用专有地址 使用 GitLab Runner 可以自动执行 GitLab CI/CD 管道…...
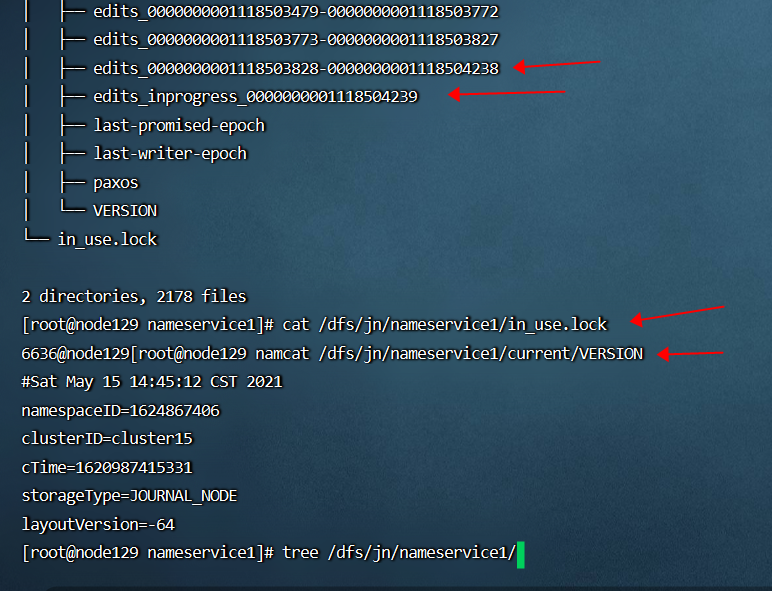
盘点下常见 HDFS JournalNode 异常的问题原因和修复方法
盘点下常见 HDFS JournalNode 异常的问题原因和修复方法 最近在多个客户现场以及公司内部环境,都遇到了因为 JournalNode 异常导致 HDFS 服务不可用的问题,在此总结下相关知识。 1 HDFS HA 高可用和 JournalNode 概述 HDFS namenode 有 SPOF 单点故障…...
)
深入了解python生成器(generator)
生成器 生成器是 Python 中一种特殊类型的迭代器。生成器允许你定义一个函数来动态产生值,而不是一次性生成所有值并将它们存储在内存中。生成器使用 yield 关键字来逐个返回值。每次调用生成器函数时,函数会在 yield 语句暂停,并记住当前的…...
【Linux】Xshell和Xftp简介_安装_VMware虚拟机使用
1、简介 Xshell简介 Xshell是一款强大的安全终端模拟软件支持SSH1、SSH2以及Microsoft Windows平台的TELNET协议。该软件通过互联网实现到远程主机的安全连接,并通过其创新性的设计和特色帮助用户在复杂的网络环境中高效工作。Xshell可以在Windows界面下访问远端不…...

【轮询负载均衡规则算法设计题】
一、题目描述 给定n台主机(编号1~n)和某批数据包,数据包格式为(抵达主机时刻,负载量)。这里数据每个时刻最多只有1条数据到达。负载量表示该主机处理此数据包总耗时。请计算轮询负载均衡规则下,…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
